
Предмет: геометрия
Класс: 7
Урок 1.
Точки, прямые, отрезки.
Цели урока: дидактическая: ознакомить учащихся с новым для них предметом, с историей развития науки геометрии, с основными геометрическими фигурами на плоскости;
развивающая: развивать логическое мышление, память, пространственное воображение, познавательный интерес, расширять представления учащихся об окружающем мире, поддерживать интерес к изучаемому предмету;
воспитательная: прививать аккуратность и трудолюбие, умение выслушивать других, формировать стремление к самореализации.
Оборудование: персональный компьютер, мультимедийный проектор, интерактивная доска, карточки, презентация «Прямая. Отрезок»
Ход урока
I. Организационный момент.
Записать тему урока, сформулировать цели.
II. Вводная беседа о возникновении и дальнейшем развитии геометрии (8 -10 минут).
Геометрия – это предмет для тех, кому нравится фантазировать, рисовать, рассматривать, кто умеет наблюдать, замечать и делать выводы. Геометрия, наверное, самая древняя наука и возникла она из практических потребностей людей.
С геометрическими фигурами и их свойствами имел дело и кожевник, резавший кожу, и кузнец, ковавший железные изделия, и портной, и строители храмов, дворцов, пирамид. Дошедшие до нас памятники и письменные документы древности свидетельствуют о том, что уже около 4000 лет тому назад жители Египта обладали значительным запасом геометрических сведений.
Заслуги в деле дальнейшего накопления и систематизации геометрических сведений принадлежат ученым Древней Греции. К III в. до н.э. в Греции накопился богатый геометрический материал, который необходимо было привести в строгую логическую систему. Первым, кто начал получать геометрические сведения при помощи рассуждений (доказательств), был древнегреческий математик Фалес (УI в. до н.э.).
Постепенно геометрия становилась наукой, в которой большинство сведений устанавливалось путем выводов, рассуждений, доказательств. Систематизацию знаний выполнил Евклид, создавший руководство по математике под названием «Начала». «Начало» почти 2000 лет служило основной книгой, по которой изучали геометрию. В этой книге геометрия впервые предстала как математическая наука. Геометрия, которая изучается в школе, называется евклидовой. Слово «геометрия» греческое, в переводе на русский язык означает «землемерие» («гео» - по-гречески земля, а «метрео» - мерить).
В геометрии изучали формы, размеры, взаимное расположение предметов и т. д.
На уроках математики вы познакомились с некоторыми геометрическими фигурами и имеете представление, что такое точка, прямая, отрезок, луч, угол, как они могут быть расположены относительно друг друга. Вы знакомы с понятиями круг, прямоугольник, квадрат, треугольник. Геометрия дает не только понятия о фигурах, но и понятия о том, какими свойствами они обладают.
Из данной мини-лекции некоторые положения дать под запись в тетради учащимся.
III. Изучение нового материала.
Мы начнем изучение геометрии с планиметрии. Планиметрия - это раздел геометрии, изучающий свойства фигур на плоскости.
Основными геометрическими фигурами на плоскости являются точка и прямая.
1. Точка – это неопределяемое понятие геометрии. Она не имеет никаких размеров, условно обозначается на бумаге остро отточенным карандашом (на доске мелом). Чтобы отличить одну точку от другой, их обозначают прописными буквами латинского алфавита: А,В, С, D…
Задание 1. Отметьте в тетради (на доске) три различные точки и обозначьте их.
2.
 Прямая – это неопределяемое
понятие геометрии. Представление о прямой дает туго натянутая нить. Евклид
писал, что у прямой нет ни длины, ни ширины, изобразить прямую целиком
невозможно, мы лишь условно изображаем ее часть. Для изображения прямых на
чертеже пользуются линейкой. Прямые обозначаются малыми латинскими
буквами либо двумя большими буквами, соответствующими концам отрезка прямой.
Прямая – это неопределяемое
понятие геометрии. Представление о прямой дает туго натянутая нить. Евклид
писал, что у прямой нет ни длины, ни ширины, изобразить прямую целиком
невозможно, мы лишь условно изображаем ее часть. Для изображения прямых на
чертеже пользуются линейкой. Прямые обозначаются малыми латинскими
буквами либо двумя большими буквами, соответствующими концам отрезка прямой.
рис. 1
Задание 2. Проведите в тетради (на доске) две различные прямые и обозначьте их.
В математике существуют специальные символы, позволяющие кратко записать какое - либо утверждение. Символы ∈ и ∉ означают соответственно «принадлежит» и «не принадлежит» и называются символами принадлежности.
 Задание
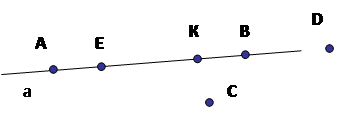
3.Отметьте точку С, не лежащую на данной прямой и точки
D, Е, К, лежащие на этой же прямой. (Рис. 2)
Задание
3.Отметьте точку С, не лежащую на данной прямой и точки
D, Е, К, лежащие на этой же прямой. (Рис. 2)
рис. 2
Используя символы принадлежности запишем.
K ∈ a, или K ∈ AB, E ∈ a, или E ∈ AB,
D ∈ a, или D ∈ AB, C ∉ a, или C ∉ AB.
Можно сказать, что прямая a проходит через точки А, K, B, E, D, но не проходит через точку C.
Задание 4. Используя символы принадлежности, запишите предложение. Точка D принадлежит прямой АВ, а точка С не принадлежит прямой a.
(D ∈ АВ, С ∉ а.)
C![]()
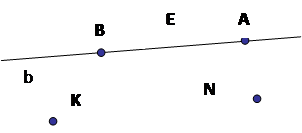
Задание 5. Используя
рисунок и символы ∈ и ∉ , запишите, какие
точки принадлежат прямой b, а какие - нет.
 |
|||||||
|
|||||||
( F ∈ b, В ∈ b, А ∈ b, С ∈ b;K ∉ b,E ∉ b,N ∉ b ).
Сколько прямых можно провести через заданную точку А?
Через любые две точки можно провести прямую?
Сколько прямых можно провести через две точки?
Итак, через любые две точки провести прямую и притом только одну.
Это утверждение назовём свойством прямой.
Задание 6. Начертите прямые XY и МК, пересекающиеся в точке О.
Для того, чтобы кратко записать, что прямые XY и МК пересекаются в точке О, используют символ ∩ и записывают так: XY ∩ MK=O.
Символ ∩ означает пересечение.
Сколько общих точек может быть у двух прямых?
Сколько общих точек может быть у двух прямых?
Таким образом, две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задание![]() 7. На прямой а отметьте
последовательно точки А, В, С, D. Запишите все
получившиеся отрезки.
7. На прямой а отметьте
последовательно точки А, В, С, D. Запишите все
получившиеся отрезки.
(отрезки АВ, ВС, CD, AC, AD, BD.)
Отрезок – часть прямой, ограниченная двумя точками
Задание 8.Начертите прямые а и b, пересекающиеся в точке М. На прямой а отметьте точку N, отличную от точки М.
а) являются ли прямые MN и а различными прямыми?
б) может ли прямая b проходить через точку N?
Рассмотрим прием «проведения» длинных отрезков прямых на местности. Этот прием заключается в следующем. Сначала отмечают какие-нибудь точки A и В. Для этой цели используют две вехи — шесты длиной около 2 м, заостренные на одном конце для того, чтобы их можно было воткнуть в землю. Третью веху ставят так, чтобы вехи, стоящие в точках A и В, закрывали ее от наблюдателя, находящегося в точке A. Следующую веху ставят так, чтобы ее закрывали вехи, стоящие в точках В и С, и т. д. Ясно, что таким способом можно построить сколь угодно длинный отрезок прямой.
Описанный прием называется провешиванием прямой (от слова «веха»). Он широко используется на практике, например при рубке лесных просек, при прокладывании трассы шоссейной или железной дороги, линий высоковольтных передач и т. д.
IV.Физминутка
Исходное положение – стоя, руки в стороны. Сжимая и разжимая ладошки дети изображают прямые, отрезки и лучи.
Исходное положение – сидя. Если они считают, что предложение истинное, то встают, руки вперед. Иначе – встают, руки вверх.
V. Проверочная работа.
Выполняет весь класс, одного ученика вызвать к доске, по окончании работы проверить ее всем классом, исправляя ошибки на доске и в тетради.
• Начертите прямую, назовите ее любой буквой.
• Отметьте точку на прямой, дав ей название.
• Начертите две прямые. Отметьте точку, дав ей название, вне прямой (сделать соответствующие записи).
• Начертите m, n, пересекающиеся в точке D. Поставьте точки, лежащие и не лежащие на этой прямой (сделать соответствующие записи).
VI. Итоги урока.
• Сколько прямых можно провести через две точки?
• Сколько общих точек могут иметь две прямые?
• Как обозначаются точки и прямые?
• Что такое геометрия, планиметрия?
• Что такое точка, прямая?
VII. Рефлексия
VIII. Задание на дом.
§ 1,2, вопросы 1-3. . 2.'Решить задачи № 1, 3,4, 7. Дома внимательно прочитать пункты 1 и 2, и к следующему уроку подготовить ответы на вопросы 1-3 на стр. 25.
Используемая литература
ü Атанасян А.С. Геометрия 7-9 М.: Просвещение 2016
ü Атанасян А.С. Изучение геометрии в 7-9 классах М.: Просвещение 2010
ü Гаврилова Н. Ф. «Поурочные разработки по геометрии 7 класс» М.: ВАКО 2004.
ü Глейзер Г. И. История математики в школе М.: Просвещение 2011
ü Зив Б. Г. «Дидактические материалы по геометрии 7» М.: Просвещение 2016
ü Использованы ресурсы сайта http://it-n.ru Савченко Е.М. (Материалы курса Мультимедийные презентации для уроков математики. Геометрия).
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.