Практическая работа № 3

Тема: Алгебра логики. Основные логические операции.

Учебная цель: Изучить основные логические операции, научиться строить таблицы истинности, схемы логических устройств.

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

Уметь:

- строить таблицы истинности,

- по логическому выражению строить схему,

- по схеме определять выражение.

Знать:

- логические операции,

- порядок построения таблицы истинности логических операций,

- базовые логические операции,

Краткие теоретические и учебно-методические материалы по теме

Высказывание – это любое предложение, в отношении которого имеет смысл утверждать о его истинности или ложности.

Логическая операция КОНЪЮНКЦИЯ (логическое умножение):

• в естественном языке соответствует союзу и;

• в алгебре высказываний обозначение &;

• в языках программирования обозначение And.

Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Таблица истинности функции логического умножения.

Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):

• в естественном языке соответствует союзу или;

• обозначение v;

• в языках программирования обозначение Оr.

Дизъюнкция — это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

Таблица истинности функции логического сложения.

Логическая операция ИНВЕРСИЯ (отрицание):

• в естественном языке соответствует словам неверно, что и частице не; _

• обозначение Ā;

• в языках программирования обозначение Not.

Отрицание — это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Таблица истинности функции логического отрицания.

Таблицы истинности.

Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).

При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.

Во-первых, необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно n, то: количество строк =2n.

Во-вторых, необходимо определить количество столбцов, а таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

В нашем случае количество переменных равно двум, а количество логических операций — пяти, то есть количество столбцов таблицы истинности равно семи.

В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных.

В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности. Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

Базовые логические элементы реализуют три основные логические операции:

• логический элемент "И" — логическое умножение;

• логический элемент "ИЛИ" — логическое сложение;

• логический элемент "НЕ" — логическое отрицание.

Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс — логический смысл сигнала — 1, нет импульса — 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.

Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.

Ниже приведены условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).

Рис. Конъюнктор,             дизъюнктор                           инвертор

Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.

Задачи практической  работы:

1. Выполнить практическую  работу;

2.Оформить отчёт по практической  работе;

Обеспеченность занятия (средства обучения)

Основные источники: 

1.            Учебно-методическая литература:

·              Михеева Е.В. Практикум по информации: учеб. пособие. – М., 2004.

·              Михеева Е.В., Титова О.И. Информатика: учебник. – М., 2005.

·              Семакин И.Г., Хеннер Е.К. Информатика. Задачник-практикум 8–11 кл. (в 2 томах). – М., 2002.

·              Семакин И.Г., Хеннер Е.К. Информатика. Учебник 10-11 кл. – М., 2007.

·              Уваров В.М., Силакова Л.А., Красникова Н.Е. Практикум по основам информатики и вычислительной техники: учеб. пособие. – М., 2005.

·              Угринович Н.Д. и др. Практикум по информатике и информационным технологиям 10–11 кл. – М., 2002.

2       Лист писчей бумаги формат А4 (210x297мм) с нанесенной ограничительной рамкой, отстоящей от левого края листа на 20мм и от остальных на 5мм со штампом основной надписи 15х185 мм (ГОСТ 2.104-2006).

3       Ручка с чернилами черного цвета.

4       Карандаш простой.

Вопросы для закрепления теоретического материала
к практической работе:

1. Приведите примеры ложных и истинных высказываний.

2. Назовите связки, с помощью которых образуют сложные (составные) высказывания.

3. Перечислить основные логические операции.

4. Какие базовые логические элементы вы знаете?

5. Как изображаются логические элементы: конъюнктор, дизъюнктор, инвертор?

6. Что содержат таблицы истинности и каков порядок их построения?

Инструкция по выполнению практической работы

Внимательно изучить раздаточный и краткий теоретический материал.

Изучить порядок выполнения задания.

Методика анализа результатов, полученных в ходе практической  работы

Контролем  является защита отчета по  практическому занятию.

Задания практической работы:

Задание 1. Даны простые высказывания:

А = {Принтер — устройство ввода информации},

В = {Процессор — устройство обработки информации},

С = {Монитор — устройство хранения информации},

D = {Клавиатура — устройство ввода информации}.

Определите истинность составного высказывания:      (A & B) & (C v D)

Задание 2. Записать составное высказывание "(2.2=4 и 3.3=9) или (2.2¹4 и 3.3¹9)" в форме логического выражения. Построить таблицу истинности.

Задание 3. Составить составное высказывание, содержащее операции логического умножения, сложения и отрицания. Определить его истинность.

Задание 4. По данной логической схеме определить логическую функцию F (А, В).

Задание № 5. Построить логические схемы по логическому выражению:

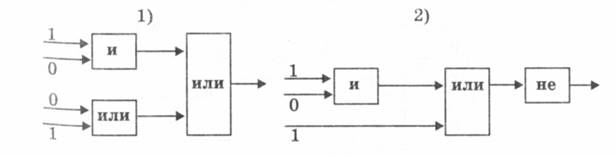
Задание № 6. Выполните вычисления по логическим схемам. Запишите соответствующие логические выражения