ОСНОВНЫЕ ПОНЯТИЯ

И ФОРМУЛЫ

521. Л КОМБИНАТОРИКИ

Перестановки

На практике часто приходится решать задачи, в которых надо составить ту или иную комбинацию элементов согласно поставленному в условии задачи требованию, а также производить подсчет числа составленных комбинаций. Такие задачи получили название комбинаторные, а раздел математики, в котором изучаются комбинаторные задачи, — комбинаторика.

Идеи и методы комбинаторики используются в теории вероятностей, математической статистике, а также в других разделах науки и техники.

Простейшей комбинацией, которую можно составить из элементов конечного множества, установив в этом множестве порядок его элементов, является перестановка.

Рассмотрим задачу.

На полке стоят три книги. Сколькими способами можно расставить эти книги на полке?

Обозначим книги буквами а, Ь, и с.

Если первой поставить книгу а, то возможны варианты abc, ась.

Если первой поставить книгу Ь, то имеем такие варианты: Ьас, Ьса.

И, наконец, если первой будет книга с, то получим такие варианты:

саЬ, cba.

Значит, три книги на полке можно расставить шестью различными способами, или, как говорят в комбинаторике, можно получить 6 различных перестановок.

О п р е д е л е н и е. Конечное множество, в котором установлен порядок его элементов, называют перестановкой.

Выясним, сколько перестановок можно получить из множества, содержащего п элементов.

зво                Гл ава

Обозначим число перестановок из п элементов символом Рп (читают: «пэ из эн»).

Если п = 1, то Р1 = 1. Это очевидно.

Если п = 2, то Р2 = 2, так как возможны лишь две перестановки: аЬ и ba.

Если п = З, то Рз = 6. Этот случай рассмотрен выше.

Пусть п = 4. Добавим к трем книгам а, Ь и с еще одну — книгу d.

Из каждой перестановки, например abc, можно получить 4 различных перестановки, если книгу d поставить перед а, перед Ь, перед с, после с:

dabc, adbc, abdc, abcd.

Всего перестановок из З элементов будет 6. Значит, Р4 = 4Р3 = 4 - 6 = 24.

Из рассмотренных примеров видно, что

= 1, Щ = 1 - 2, Н = 1 - 2 . З, Щ = 1 - 2 - 3 - 4.

Можно предположить, что число перестановок из п элементов можно найти по формуле

                        Р— 1 . 2 - 3  (п — 1)n.

Произведение первых п натуральных чисел принято обозначать так: п! (читают: «эн факториал»), т. е. п! = 1 • 2 • З 1)n. По определению также считают, что 1! = 1.

Докажем, что для любого п € N верна формула

(1)

Доказательство проведем методом математической индукции. При п = 1 формула (1) верна: Р1 = 1, т. е. Р1 = 1!

Допустим, что формула (1) верна для п = К, где > 1, т. е. РК = К! Докажем, что формула (1) также верна для п = + 1, т. е.

Пусть ща2аз.. .ак — произвольная перестановка, которую можно составить из элементов. Если к этой перестановке присоединить элемент, то его можно поставить на первое место, на второе место и т. д., на h-e место и, наконец, на последнее место (после ак элемента).

В результате из одной перестановки можно получить + 1 перестановку, а из РК перестановок — (К + 1)Рк перестановок. ЗнаЧИТ, РК +1 = (К + 1)Ph = (К + 1)hl = (К + 1)!

Мы показали, что формула (1) верна для п = 1, и, допустив, что она верна для п = К, доказали, что она верна для п = К + 1. Следовательно, на основании принципа математической индукции формула (1) верна для любого п > 1.

Пр имер 1. Найдем, сколько различных четырехзначных чисел можно составить, используя цифры О, 1, 2, З, причем в каждом числе цифры должны быть разные.

Количество четырехзначных чисел, которые можно составить из четырех различных цифр, исключая О, без повторения цифр, равно числу перестановок из четырех элементов, т. е. Р4. Однако в этом случае среди цифр есть цифра О, с которой не может начинаться четырехзначное число. Поэтому из перестановок, содержащих четыре элемента, надо исключить те перестановки, которые начинаются цифрой О. Таких перестановок будет Рз. Следовательно, всего четырехзначных чисел, которые можно составить из данных цифр, будет

Р4 - = 4 - 3! = - 1) = 6 - 3 = 18. Ответ: 18.

П р и мер 2. Имеется 10 различных книг, среди которых есть трехтомник одного автора. Сколькими способами можно расставить эти книги на полке, если книги трехтомника должны находиться вместе, но в любом порядке?

Будем считать трехтомник одной книгой. Тогда у нас имеется не 10 книг, а 8. Расставить их можно Р8 различными способами. В то же время книги в трехтомнике можно расставить Рз способами, каждой перестановке из 8 элементов соответствует определенная перестановка из З элементов. Поэтому всего перестановок в соответствии с условием задачи будет

 • = 8! • 3! = 241 920. Ответ: 241 920.

1337.                 Сколькими различными способами могут сесть на скамейку

а) 5 человек;         б) 7 человек?

1338.                 Сколько различных трехцветных флагов с тремя горизонтальными полосами можно получить, используя красный, синий и белый цвета?

1339.                 Сколькими способами можно расставить по этапам четырех участниц эстафеты в беге 4 х 100 м?

1340.                 Составьте всевозможные трехзначные числа, в которых все цифры разные, используя лишь цифры:

1341.                 Сколько четных трехзначных чисел можно составить из цифр 1, 2, 5, 7, если каждая цифра может быть использована только один раз?

Гл ава

1342.                 Учащиеся должны посетить во вторник по расписанию 5 уроков по следующим предметам: литература, алгебра, география, физкультура и биология. Сколькими способами можно составить расписание на этот день так, чтобы физкультура была пятым уроком?

1343.                 Из цифр 2, З, 4, 7 составлены всевозможные четырехзначные числа (без повторения цифр). Сколько среди этих чисел таких, которые:

а) начинаются с цифры 7;           б) не начинаются с цифры 4?

1344.                 Из цифр 1, 2, О, 5, 6 составлены всевозможные пятизначные числа (без повторения цифр). Сколько среди этих чисел таких, которые:

а) кратны 4;         б) кратны 5?

1345.                 В автомашине 5 мест. Сколькими способами в этой автомашине могут разместиться 5 человек, если место водителя могут занять только двое из них (т. е. только двое могут управлять автомобилем)?

1346.                 Чтобы открыть сейф, нужно набрать шифр, содержащий определенную последовательность из цифр 1, 2, З, 4, 5, 6, и другой шифр, содержащий последовательность из букв а, Ь, с, d, в которых буквы и цифры не повторяются. Сколько существует комбинаций, при которых сейф не открывается?

1347.                 Сколькими способами можно расставить на полке четыре книги по алгебре и три по геометрии, причем так, чтобы все книги по алгебре (в любом порядке) стояли рядом?

1348.                 Найдите сумму всех трехзначных чисел, которые можно составить из цифр 2, 4, 6, не повторяя цифр?

1349.                 Число а = п! + 1, где п € N, является квадратом натурального числа. Найдите наименьшее значение а, если:

а) а — двузначное число;        б) а — трехзначное число.

1350.                 Решите уравнение:

а) х! = 5040;        6) х! + (х - 1)! = 5760.

1351.                 Постройте график функции у = 2х² - 31xl - 2.

1352.                 При каких значениях параметра а уравнение .х⁴ + ах ² + а — 1 = О имеет только два корня?

2 - х

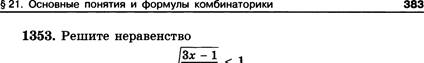
1354. Докажите, что значение выражения

есть натуральное число.

Составим из элементов множества {а, Ь, с, d} всевозможные пары, чтобы в каждой паре элементы не повторялись.

В первой строке запишем все пары с первым элементом а, во второй — все пары с первым элементом Ь и т. д. Получим таблицу:

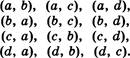
Каждую пару в этой таблице, составленную из элементов множества {а, Ь, с, d}, в комбинаторике называют размещением из 4 элементов по 2. Число всех таких размещений обозначают так:

(читают: «а из четырех по два»). Мы видим, что            = 4 • З = 12.

Определение. Размещением из п элементов конечного множества по К, где < п, называют упорядоченное множество, содержащее элементов.

Таким образом, размещения — это пары, тройки, четверки и т. д. элементов множества. Из определения следует, что два размещения являются различными, если они отличаются друг от друга элементами или порядком элементов. Легко видеть, что размещение из п элементов по п — это перестановка из п элементов.

Символом АК обозначается число всевозможных размещений, которые можно составить из п элементов по К.

Теорем а. Число размещений, составленных из п элементов по К, вычисляется по формуле

АК = п(п — 1)(n — 2) • ... • (п — (К — 1)),

т. е. равно произведению последовательных натуральных чисел, большим из которых является п.

Д о к аз а т е л ь с т в о. Пусть имеется множество, состоящее из п элементов:

Глава

Мы не знаем, сколько всего можно составить размещений из этих п элементов по К, но знаем, что среди всех размещений есть такие, которые начинаются элементом а. Поставим себе задачу сосчитать, сколько размещений из п по начинаются элементом а.

Пусть

К элементов одно из таких размещений. В таком размещении — 1 элементов, следующих после а, представляют собой некоторое размещение из п — 1 элементов по — 1. Действительно, в это размещение могут входить любые из данных п элементов, кроме элемента а. Поэтому размещений из п элементов по К, начинающихся элементом а, столько, сколько можно составить размещений из п — 1 элементов по — 1.

Каэкдое из размещений из п по начинается либо элементом а, либо элементом Ь и т. д.

Число размещений, начинающихся элементом а, равно An^h _}. Точно так же число размещений, начинающихся элементом Ь, равно и т. д. Число всех размещений из п по К, т. е. А; , равно сумме чисел размещений, начинающихся на а, Ь, с

Всего элементов в данном множестве п. Следовательно,

Эта формула верна для любого п > 1 и < п. Значит, Ап^к _} = (п —  т. е. =          — 1)Щ_;. Далее

An^h _; = (П - 2)

Отсюда

                                 А^КП =      — 1)(n —

Продолжая эти рассуждения далее, получим формулу „4: = — 1)(n — 2) • . . .

Подставляя в эту формулу (1) вместо число п, получим АК = п(п — 1)(n — 2) . . . 2 - 1 = п!

Это еще раз подтверждает, что размещение из п элементов по п является перестановкой из п элементов.

По определению принято считать, что О! = 1. Поэтому формуле (1) можно придать другой вид, если ее правую часть умножить на дробь (п — К)! ' равную 1:

     А: =    — 1)(n — 2) • . . . • (п — (К — 1)) •

п!

Пример 1. Из 12 учащихся нужно отобрать по одному человеку для участия в городских олимпиадах по математике, физике, истории и географии. Каждый из учащихся участвует только в одной олимпиаде. Сколькими способами это можно сделать?

Каждая группа учащихся, направляемая на олимпиаду в составе 4 человек, отличается от любой другой группы либо учащимися, либо порядком, который определяет, по какому предмету будет соревноваться ученик. Поэтому число способов отбора учащихся равно числу размещений из 12 по 4:

 = 12 • 11 • 10 - 9 = 11 880.

Ответ: 11 880.

При мер 2. Сколько существует семизначных телефонных номеров, в которых все цифры различны и первая цифра отлична от нуля?

Количество всех семизначных номеров из 10 цифр (без повторений) будет Аш. Из них нужно исключить те номера, которые начинаются цифрой О. Таких номеров Ад. Значит, всего номеров, согласно условию, будет

= - 1) = 544 320. (10 - 7)! - (9

Ответ: 544 320.

Пример З. Сколько существует трехзначных чисел, составленных из цифр 1, 2, З, 4, 5, 6 (без повторений), которые не кратны З?

Числа, кратные З, — это числа, которые составлены из цифр

только из этих цифр. Из каждой тройки цифр можно составить Ра чисел, кратных З (сумма цифр числа, записанного в любом порядке, кратна З). Всего троек 8. Значит, всего трехзначных чисел, кратных З, будет

8 . Ра = 8- 6 = 48.

Всех трехзначных чисел, которые можно составить из данных 6 цифр, будет Аб, т. е. 120. Значит, количество трехзначных чисел, не кратных З, равно

- 8Р3 = 120 - 48 = 72.

Ответ: 72.

1355. Сколькими способами могут быть присуждены первая, вторая и третья премии трем лицам из 10 соревнующихся?

13 Ю. Макарычев «Алгебра. 9 кл..

Гл ава

1356.                 На станции имеется 8 запасных путей. Сколькими способами можно расставить на них четыре поезда?

1357.                 Сколькими способами можно изготовить трехцветный флаг с горизонтальными полосами из материала, имеющего 5 различных цветов?

1358.                 Из цифр 1, 2, З, 4, 5, 6 составьте четырехзначные числа, в которых все цифры различны, а первой цифрой является 1, второй — З. Сколько таких чисел?

1359.                 В вагоне имеется 10 свободных мест. В вагон вошли 6 пассажиров. Сколькими способами они могут разместиться в этом вагоне на свободных местах?

1360.                 Учащиеся школы изучают 12 различных предметов. Сколькими способами можно составить расписание уроков на один день, чтобы в нем было 5 различных предметов? 1361. Вычислите:

в)

1362.                 Из цифр 1, 2, З, 4, 5 составлены всевозможные трехзначные числа (без повторения цифр). Сколько среди них таких, которые:

а) кратны 2;          б) кратны З;          в) кратны 4;          г) кратны 5?

1363.                 Сколько различных натуральных чисел, меньших 1000, можно составить из цифр 1, 2, З, 4, 5, 6, 7 без повторения цифр в числе?

1364.                 Решите уравнение:

а) АК = 20А\; 6) А: = 12А²п. 1365. Найдите значение выражения

где т € N, п                  < т.

1366.      Сколькими способами можно расклеить 12 различных марок на трех листах?

+4--4+-4- ф Упражнения для повторения

1367.      Решите уравнение:

б)  11.

1368.      Решите неравенство:

      3х ² + 4х — 4                          3х ² + 2х - 1

а)                    6) х ² — х + 1

1369.      Постройте график функции

Рассмотрим множество {а, Ь, с, d} и составим все подмножества этого множества, содержащие два элемента. Получим

О п р е д е л е н и е. Подмножества, составленные из п элементов данного множества и содержащие элементов в каждом подмножестве, называют сочетаниями из п элементов по К.

В отличие от размещений, сочетания различаются только элементами. Так {а, b} и {b, а} — одно и то же сочетание.

Число сочетаний из п элементов по обозначается так: Оп. В рассмотренном выше примере С4 = 6.

Докажем, что число сочетаний, составленных из п элементов по К, выражается формулой

Пусть имеется некоторое множество, содержащее п элементов, и допустим, что мы составили из элементов этого множества всевозможные сочетания из п по К. Число таких сочетаний равно С:. В каждом сочетании произведем перестановку элементов всеми возможными способами. Каждое сочетание даст РК перестановок. В результате мы получим все размещения, которые можно составить из п элементов по К. Таким образом,

Отсюда

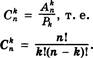
По определению сочетание — это подмножество данного множества.

зев               Гл ава

Выясним, сколько подмножеств имеет данное множество, содержащее п элементов.

Обозначим число подмножеств множества А, содержащего п элементов, так: Мп(А).

Если А = т, то оно, очевидно, содержит лишь одно подмножество — это а. Значит, Мо(А) = 1.

Пусть А = {щ}, т. е. множество содержит один элемент. Тогда число подмножеств равно 2: и {ад. В этом случае М1(А) = 2.

Пусть А = {щ, щ}. Тогда число подмножеств множества А равно 4: а, {щ}, {щ}, {щ, ф}, т. е. М2(А) = 4 = 2 ² .

Аналогично можно посчитать, что Мз(А) = 2³ , М4(А) = 2⁴ .

Подсчитаем число подмножеств множества А, содержащего

5 элементов. Для этого воспользуемся формулой С: =

        Вычислим по отдельности числа СЕ, С}, С}, Й,          СЕ.

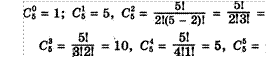 = 10,

Отсюда

+ + + + + = 1 + 5 + 10 + 10 + 5 + 1 = 32 = 2⁶

Итак, мы видим, что сд = 2⁰ , с? + с} + 1 = 2 ¹ , с; + + с; = 1 + 2 + 1 = 2²

+ + + с: + с: + = 2⁵ .

Можно предположить, что число подмножеств множества А, содержащего п элементов, равно т. е. Мп(А) =

Докажем ето методом математической индукции.

Если п = 1, то М1(А) = 2 ¹ , т. е. формула верна. Пусть п > 1. Рассмотрим множество

Исключим из этого множества элемент ап. Получим множество, содержащее п — 1 элемент. По предположению индукции

Мп-1(А) =

Добавим к множеству исключенный элемент ап. Тогда из каждого подмножества „41 = {ар ат ... , ап- 1} образуется новое подмножество, в которое входит элемент ап, т. е. число подмножеств по сравнению с числом подмножеств множества „41 увеличится вдвое, и множество будет содержать 2 • 2 ^п подмножеств, т. е. 2^п . Значит, формула Мп(А) = 2 ^п верна.

Отсюда следует, что

В процессе рассуждений мы заметили, что С; = С: — СК ¹ и вообще Сп = СК ^к.

Докажем это.

Составим таблицу, в которой в первой строке запишем значение Со, во второй строке — значения С? и 01, в третьей строке — значения С2, (2¹2, С2 и т. д. Получим

1

                          1  1

                                  1 2      1

                                    1 З З         1

                                    1 4 6         4      1

                                    1 5 10 10       

1 6 15 20 15 6 1

Эта таблица называется треугольником Б. Паскаля (1623— 1662), выдающегося французского ученого-математика, физика, философа, который, в частности, занимался исследованиями в области комбинаторики.

В этой таблице на пересечении п-й строки и К-го столбца (п > О,  > О) записано число, равное С:.

Хорошо видна закономерность строк: числа, одинаково удаленные от начала и конца строки, равны. Это следует из того, что верно равенство С: = СК - ^к. Кроме того, складывая числа 5 и 10 (в 6-й строке), мы получаем число 15, которое стоит в 7-й строке под числом 10. Это вытекает из равенства

Заметим также, что числа каждой строки треугольника Паскаля равны коэффициентам многочлена, полученного от возведения в п-ю степень двучлена а + Ь. Например,

(а + = а² + 2ab + b² ,

(а + = а^з + 3a²b + Зан + Ы,

(а + = а⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ .

Рассмотрим примеры задач, в которых используется формула числа сочетаний из п элементов по К.

Пр имер 1. Сколькими способами можно выбрать трех дежурных из класса, в котором 20 человек?

Очевидно, что здесь речь идет о сочетаниях, так как каждая группа учащихся в З человека должна отличаться хотя бы одним из учащихся. Следовательно, таких групп должно быть сп.

                                         201           20. 19 • 18

     Значит, С20 = 3!17!                         1140.

Ответ: 1140.

Пример 2. Из вазы с цветами, в которой стоят 10 красных гвоздик и 5 белых, выбирают 2 красные гвоздики и одну белую. Сколькими способами можно сделать такой выбор букета?

Каждый выбор содержит З цветка, в котором 2 гвоздики красные и 1 белая. Выбрать 2 красные гвоздики из 10 красных можно Сю способами. После этого белую гвоздику можно выбрать С5 способами.

Каэкдому выбору красных гвоздик соответствует определенный выбор белой гвоздики. Поэтому выбор букета из двух красных и одной белой гвоздик можно сделать Сш • С5 способами.

      Имеем       • С: = 45 . 5 = 225.

Значит, выбор букета, о котором говорится в задаче, можно осуществить 225 способами.

Пример З. Семь огурцов и три помидора надо положить в два пакета так, чтобы в каждом пакете был хотя бы один помидор и чтобы овощей в пакетах было поровну. Сколькими способами это можно сделать?

Чтобы в пакетах овощей было поровну, в каждом пакете должно находиться 5 овощей. Если положить в один пакет один помидор, то остальные овощи — 4 огурца — можно положить в этот пакет С7 способами.

Если в другой пакет положить 2 помидора, то остальные овощи — З огурца — можно положить в этот пакет С7 способами.

Следовательно, в первый пакет овощи можно разложить Сз • С;

                          7!  3 - 7 . 6 - 5

способами, т. е. З¯б¯¯ = 105 способами. Во второй пакет овощи можно разложить С; • Ст, т. е. З = 105 способами.

Согласно условию задачи в обоих пакетах овощей будет ровну.

От в е т: овощи в два пакета можно разложить 105 способами.

1370.                  Из спортсменов А, Б, В, Г, Д и Е выбирается пара для участия в соревнованиях пар по теннису. Сколько существует способов выбора этой пары?

                                     комбинаторики

1371.                  На плоскости отмечены 10 точек, причем никакие три из них не лежат на одной прямой. Через каждые две из них проведена прямая. Сколько проведено прямых?

 1372. Сколько диагоналей имеет выпуклый двенадцатиугольник?

1373.                 Сколькими способами можно упаковать 17 различных книг в две пачки, по 8 и 9 книг в каждой?

1374.                 Сколько нечетных делителей имеет число 3570? Сколько четных делителей имеет это число?

1375.                 Дано множество Х = {а, Ь, с, d}. Составьте все подмножества множества Х, которые

а) не содержат элемента а;           б) не содержат элементов Ь и d.

1376.                 Сколько подмножеств имеет множество, содержащее:

а) 8 элементов;                            б) 10 элементов?

1377.                 Из 10 разных цветков нужно составить букет, содержащий З цветка, 5 цветков, 7 цветков, 9 цветков. Сколькими способами это можно сделать?

1378.                 Сколько можно составить из делителей числа 210 составных чисел, которые содержат:

а) только два простых делителя;

б) только три простых делителя?

1379.                 Сколько членов содержит многочлен аЬс + abd + ... + hlm, составленный из 12 переменных, в котором каждый член является произведением трех множителей и нет подобных членов?

1380.                 Решите уравнение:

в) 14С: ² - 15А} 3,

 = 114² -1.

1381.                 Сколько человек участвовали в шахматном турнире, если известно, что каждый участник сыграл с каждым из остальных по одной партии и всего было сыграно 136 партий?

          Упражнения для повторения

1382.                 Укажите номера положительных членов последова-

бп — п ²

тельности (ап), если ап =       5    

1383.                 Докажите, что многочлен х⁴ — 4х³ — 6х² — 3х + 9 не имеет отрицательных корней.

1384.                 Постройте треугольник с вершинами А(О; З), В(З; О), С(5; 6) и задайте его системой неравенств с двумя переменными.

-4-4-.+-4-.+--4-— ф Контрольные вопросы и задания

1.     Что называется перестановкой из п элементов? Выведите формулу числа перестановок из п элементов.

2.     Дайте определение размещения из п элементов по и выведите соответствующую формулу.

З. Дайте определение сочетания из п элементов по К. Выведите соответствующую формулу.

ЭЛЕМЕНТЫ

22. Л ТЕОРИИ ВЕРОЯТНОСТЕЙ

                  60.             Частота и вероятность

Мы живем в мире, где наряду с событиями, непременно наступающими (например, смена времени года), происходят события, зависящие от случая. Случайно перегорела лампочка, случайно произошло замыкание и начался пожар, купленный лотерейный билет случайно оказался выигрышным. Все это события, которые заранее предсказать невозможно.

Событие, которое в процессе наблюдения или испытания (эксперимента) может произойти или не произойти, называют случайным событием.

Приведем еще примеры случайных событий: поражение мишени или промах в результате произведенного выстрела, выигрыш или проигрыш футбольной команды в матче, выпадение орла или решки при подбрасывании монеты — все это случайные события.

Пусть определенное испытание повторяется много раз и при этом каждый раз фиксируется, произошло или нет интересующее нас событие А. Обозначим буквой п общее число испытаний, а буквой т — число появлений события А в результате проведенных п испытаний. Тогда отношение называют частотой случайного события А.

Статистика показывает, что при повторении одного и того же опыта (или наблюдения), допускающего многократное его повто-

рение в одних и тех же условиях, частота появления ожидаемого случайного события остается примерно одинаковой, незначительно отличаясь от некоторого постоянного числа.

 Рассмотрим такой пример. Бросают монету. Она может упасть

кверху орлом или решкой. Как часто монета падает кверху орлом?

Многие ученые проводили эксперимент. При многократном бросании монеты подсчитывалось число выпадений орла. Результаты этих опытов показаны в таблице.

	Кол-во фотов	вьпщцений ор		Кол-во фотов	вьпц:рний
Бюффон	4040	0,507	Романовский	80 640	0,4923
Де Морган	4092	0,5005	Пирсон К.	24 000	0,5005
Джевонс	20 480	0,5068	Феллер	10 000	0,4979

Из таблицы видно, что выпадение орла во всех случаях близ-

1

ко к

Рассмотрим другой пример.

Приведем данные о рождаемости девочек в течение года. По данным шведской статистики частота рождения девочек за 1935 год, т. е. отношение числа родившихся девочек к числу родившихся детей, характеризуется следующими числами:

январь — 0,486,	июль — 0,462,
февраль — 0,489,	август — 0,484,
март — 0,490,	сентябрь — 0,495,
апрель — 0,471,	октябрь — 0,491,
май — 0,478,	ноябрь — 0,482,
июнь — 0,482,	декабрь — 0,473.

Несмотря на то что общее число рождений меняется в течение года, частота рождения девочки довольно устойчиво колеблется около среднего значения 0,482. Такие статистические закономерности открыты еще в XVIII веке. Это было подтверждено демографическими материалами при изучении статистики рождаемости, смертности, несчастных случаев и т. п.

Подобные закономерности позволяют подойти к статистическому определению вероятности. Если в длинной серии экспериментов со случайными исходами, которые могут быть многократно проверены в одинаковых условиях, значения частот близки к некоторому постоянному числу, то это число принимают за вероятность данного события. Такое определение вероятности называют статистическим.

Для того чтобы найти частоту при проведении того или иного испытания, мы должны провести достаточно большое число экспериментов и лишь после этого моРис. 139 жем определить приближенно вероятность наступления интересующего нас случайного события.

В то же время если шансы наступления случайного события равновозможны, то вероятность наступления данного события можно определить путем правдоподобных рассуждений, осно-

ванных на практическом опыте и здравом смысле.

Вернемся к примеру с бросанием монеты. Если монета пра-

вильная, то нет никаких оснований полагать, что шансы выпадения орла больше, чем шансы выпадения решки (этим обычно пользуются, когда бросают жребий, например, в начале футбольного матча, какая команда должна первой ввести мяч в игру). Иначе говоря, вероятность выпадения орла такая же, как и

вероятность выпадения решки.

Рассмотрим пример с игральным кубиком, который представляет маленький куб, на гранях которого выбиты очки 1, 2, З, 4, 5, 6 (рис. 139). Если этот кубик сделан из однородного материала, то при его бросании шансы выпадания на верхней грани любого числа очков от 1 до 6 равновозможны. Говорят, что

— это множество равновозможных исходов опыта при бросании игрального кубика.

Пусть событие А означает, что при бросании кубика выпадет четное число очков. Событие А произойдет при трех исходах: выпало 2 очка, 4 очка или 6 очков. В таких случаях говорят, что эти исходы благоприятны для наступления события А.

При бросании кубика всего 6 равновозможных исходов, из них

З — благоприятны для наступления события А. Благоприятные

З для А исходы составляют б всех исходов. Это отношение называют вероятностью наступления события А и пишут

¹ .

 = 2

О пр е д еле н и е. Вероятностью события А называется отношение числа благоприятных для А исходов к числу всех равновозможных исходов.

Это определение вероятности называют классическим.

Сопоставляя классическое и статистическое определение вероятности, можно сделать вывод: нахождение классической вероятности не требует, чтобы испытание проводилось в действи-

тельности, а нахождение статистической вероятности (частоты) предполагает, чтобы испытание было проведено фактически.

Пусть В — событие, которое состоит в том, что при бросании игрального кубика выпадет четное или нечетное число очков. Найдем Р(В). В этом случае каждый исход из множества

6 является благоприятным для события В. Поэтому Р(В) =

Такие события, которые происходят всегда, сколько бы раз ни проводилось испытание, называют Достоверными. Вероятность достоверного события равна 1.

Пусть С — событие, означающее, что при бросании игрального кубика на нем выпадет более 6 очков. Очевидно, это событие произойти не может. Число благоприятных для С исходов равно нулю. Значит, Р(С) = О. Такие события называют невозможными.

Рассмотрим вообще некоторое событие М, которое при проведении испытания имеет п равновозможных исходов, причем т исходов благоприятны для наступления события М. Тогда Р(М) =

Очевидно, что т < п. Поэтому — < 1, т. е. Р(М) < 1. С другой стороны, > О, так как О < т < п. Значит, Р(М) > О. Отсюда

следует, что О < Р(М) < 1.

Рассмотрим примеры вычисления вероятностей некоторых событий.

Пример 1. В урне 10 одинаковых шаров разного цвета: 2 красных, З синих и 5 желтых. Шары тщательно перемешаны. Наугад вынимается один шар. Какова вероятность того, что вынутый шар окажется:

а) красным (событие К);

б) синим (событие С);

в) желтым (событие Ж)?

Для события К благоприятным являются 2 исхода, для события С — З исхода, для события Ж — 5 исходов.

Отсюда имеем:

                        2    1.           З .             5    1

Пр имер 2. Монету бросают дважды. Какова вероятность того, что оба раза выпадет решка; оба раза не выпадет решка?

Обозначим выпадение решки буквой р, а орла — буквой о. Тогда множество U равновозможных исходов таково: U = {ро, рр, ор, оо}.

Гл ава

Обозначим буквой А событие, что оба раза выпадет решка, а буквой В — оба раза не выпадет решка.

Для события А благоприятен один исход, а для события В три исхода Фо, ор, 00). Отсюда

                                       1            з

Такие события, как А и В, называют противоположными событияли. Событие А или В — достоверное событие:

- 1.

Обычно событие, противоположное событию А, обозначают А. В данном случае В = А.

Вообще если множество U имеет п равновозможных исходов и из них исходов благоприятны для события А, то для события А благоприятны п — исходов. Отсюда

Значит, Р(А) = 1 — Р(А).

Пр имер З. Коля и Миша бросают два игральных кубика (белый и черный). Они договорились, что если при бросании кубиков в сумме выпадет 8 очков, то выиграл Коля, а если в сумме выпадет 7 очков, то выиграл Миша. Справедлива ли эта игра?

Все равновозможные исходы при бросании двух кубиков образуют множество пар, в которых первая цифра в паре — это число очков, выпавших на белом кубике, а вторая цифра в паре — это число очков, выпавших на черном кубике. Это множество пар представлено в таблице.

		(3; 1)	(4; 1)	(5;1)
	(2,	(3; 2)	(4,	(5; 2)
	(2; З)	(3; 3)	(4,	(5; 3)
4)	(2; 4)		(4; 4)	(5,
	(2; 5)	(3; 5)	(4; 5)	(5,
	(2; б)	(3; 6)	(4; 6)	(5,

Всего равновозможных исходов 36.

Найдем вероятность того, что на верхних гранях кубиков выпадет 8 очков (событие А), выпадет 7 очков (событие В).

Для события А благоприятны 5 исходов: (2; 6), (З; 5), (4; 4), (5; З), (6; 2), а для события В благоприятны 6 исходов: (1; 6), (2; 5),

(3; 4), (4; 3), (5; 2), (6; 1). Отсюда

                                                5                  6

Значит, шансов выиграть у Миши больше, чем у Коли. Поэтому такую игру нельзя назвать справедливой.

Пр и мер 4. Из собранных 10 велосипедов только 7 не имеют дефектов. Какова вероятность того, что 4 выбранных велосипеда из этих 10 окажутся без дефекта?

Пусть А — событие, при котором все выбранные 4 велосипеда из 10 оказались исправными. Каждое сочетание из 10 по 4 является равновозможным исходом выбора 4 велосипедов из 10. Значит, всего равновозможных исходов ()10. Число исходов, благоприятых для наступления события А, равно Ст. Значит,

1

1385.                 В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Какова частота появления нестандартных деталей?

1386.                 На учениях по стрельбе из пистолета частота поражения мишени оказалась равной 0,85. Сколько попаданий в цель можно ожидать, если по мишени было произведено 120 выстрелов?

1387.                 Выберите 10 строк текста. Проведите подсчет и найдите частоту появления:

а) буквы а; б) буквы е; в) буквы к; г) буквы я.

1388.                 Найдите вероятность при бросании игрального кубика появления:

а) 2 очков;

б) числа очков, больших З;

в) 1 очка или 6 очков;

г) числа очков, меньших 6.

1389.                 Какова вероятность того, что при бросании двух игральных кубиков сумма очков на них окажется равной:

г) 12?

1390.                 В урне 10 белых, 4 черных и 6 желтых шаров одинаковых размеров. Из урны достают один шар. Какова вероятность того, что этот шар окажется:

а) белым; б) черным; в) желтым; г) белым или черным?

Гл ава

1391.                 В первой урне два белых и три черных шара, во второй урне три белых и два черных шара. Из каждой урны достали по одному шару. Какова вероятность того, что хотя бы один из двух шаров окажется белым?

1392.                 В урне 10 одинаковых шаров разного цвета: 2 белых, З красных и 5 синих. Наугад вынимаются два шара. Найдите вероятность событий:

а) А — оба шара белые;               в) С — оба шара синие.

б) В — оба шара красные;

1393.                 В урне 8 белых и 4 черных шара. Из урны извлекаются 2 шара. Найдите вероятность того, что оба шара будут белыми.

1394.                 Из 28 костей домино выбирают наугад одну кость. Какова вероятность того, что выбранная кость содержит в сумме:

а) 5 очков;           б) 6 очков;         в) 10 очков?

1395.                 В настольной игре «Пираты» участники поочередно бросают сразу два игральных кубика. Если при этом выпадает дубль, то участник делает два хода подряд. Какова вероятность того, что участнику игры удается сделать два хода подряд при очередном броске?

1396.                 Бросают З монеты. Какова вероятность того, что все они упадут решкой?

1397.                 Набирая номер телефона, абонент забыл последние две цифры и, помня, что эти цифры различны, набрал наугад. Какова вероятность того, что он с первого раза наберет нужный номер телефона?

1398.                 В гараже 7 шин из 10 без брака. Какова вероятность того, что среди 6 шин, взятых наугад, 4 окажутся без брака?

1399.                 Из 28 костей домино наугад извлекается кость. Найдите вероятность того, что вторую извлеченную кость можно приставить к первой, если первая кость:

а) оказалась дублем;       б) не является дублем.

1400.                 Из колоды в 36 карт выбирается наугад одна карта. Какова вероятность того, что это будет дама пик или туз (любой масти)?

-Н-Н-Н— Упражнения для повторения

1401.                 Является ли арифметической прогрессией последовательность, сумма первых п членов которой вычисляется по формуле:

а) sn = 2П² - 5;                  б) Sn = п^з — Зп² ;             в) Sn = 1,5n² — П ³?

1402.                 Постройте график функции:

а) у = 2х² - 31xl - 2;       б) у = х² — 4х + 12х — 11.

1403.                 Найдите область определения функций

а) у = .чб¯х•,                 

б) у = sin2x; рассматривая эти функции на промежутке 21].

Пусть при проведении одного и того же испытания наблюдаются события А, В и С. Причем событие С означает, что при испытании произошло хотя бы одно из двух событий — А или В. В таких случаях С называют объединением событий А и В и обозначают С = А U В.

Рассмотрим пример.

В мешке находятся жетоны с номерами 1, 2, З, 4, 5, 6, 7, 8, 9. Пусть событие А означает, что из мешка извлечен жетон с номером, кратным З; событие В означает, что из мешка извлечен жетон с номером, кратным 4. Какова вероятность события С, означающего, что из мешка извлечен жетон с номером, кратным З или 4?

Событие С есть объединение событий А и В, т. е. С = А U В. Множество всех равновозможных исходов в этом испытании — это множество U = {1, 2, З, 4, 5, 6, 7, 8, 9}, где цифрами обозначены номера жетонов, находящихся в мешке.

Для события А благоприятными являются исходы, при которых извлекаются жетоны с номерами З, 6 и 9, для события В — исходы с номерами 4 и 8, для события С — исходы с номерами З, 4, 6, 8, 9. Значит,

Отсюда следует

Рассмотренные в этом примере события А и В являются несовместными, т. е. любой исход не может быть одновременно благоприятным как для события А, так и для события В. Для таких событий верна теорема:

вероятность появления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий.

Глава

Докажем это.

Пусть п — общее число исходов испытания, пи — число исходов, благоприятных для наступления события А, — число исходов, благоприятных для наступления события В.

Тогда Р(А) =

Так как события А и В несовместны, то для события А U В число благоприятных исходов равно пи + пи. Отсюда

Можно доказать, что вообще вероятность объединения попарно несовместных событий 4, А Ап равна сумме вероятностей этих событий:

Р(А1 И А2 и ... U Ап) = P(Al) + Р(А2) + ... + Р(Ап).

Рассмотрим примеры, в которых применяется теорема о сложении вероятностей несовместных событий.

Пример 1. В урне находится 30 шаров: 10 белых, 15 красных и 5 синих. Найдем вероятность появления цветного шара.

Вероятность появления красного шара (событие А) равна 15

Вероятность появления синего шара (событие В) равна

События А и В несовместные (появление шара одного цвета исключает появление шара другого цвета), поэтому можно применить теорему сложения вероятностей. Вероятность появления цветного шара (либо красного, либо синего) равна и В) = Р(А) + Р(В) = 2+6 = 3'

Пример 2. В контейнере 10 деталей, из них 2 нестандартные. Найдем вероятность того, что из 6 наугад отобранных деталей окажется не более одной нестандартной.

Р еш е н и е. Пусть событие А означает, что среди отобранных 6 деталей все детали стандартные, а событие В означает, что среди отобранных 6 деталей есть одна нестандартная.

Всего равновозможных исходов Со. Благоприятных для события А исходов С8. Благоприятных для события В исходов С2 • СЕ.

Действительно, одну нестандартную деталь из 2 можно извлечь (22 способами, а оставшиеся 5 стандартных деталей — С8 способами. каждому способу извлечения одной нестандартной детали соответствует один способ извлечения 5 стандартных деталей. Поэтому число благоприятных исходов для события В равно СЕ • СЕ. События А и В несовместные. Значит,

28 112 140 2

- то + то = то = 3'

Введем еще одно понятие. Система несовместных событий „41,

Ап называется полной, если события, входящие в данную систему, являются единственно возможными.

Поясним это на примере с бросанием игрального кубика.

а) Пусть событие Ап, где 1 < п < 6, означает, что выпало п очков. Тогда система событий „41, „42, ... , 4 является полной. При этом

             P(Al             и ... И 4) = P(Al) + Р(А2) + ... + Р(4) =

б) Пусть событие С означает, что выпало не более 2 очков, а событие D означает, что выпало больше 2 очков. В этом случае система событий С и D также является полной:

Вообще если система попарно несовместных событий А1,

„42, ... , Ап является ПОЛНОЙ, ТО

               Р(А1 U               И ... U Ап) = Р (4) + Р(А2) + + Р(Ат) = 1.

Примером двух несовместных событий, образующих полную систему, являются два противоположных событияА и А. Их объединение — достоверное событие:

Отсюда Р(А) = 1 — Р(А).

При м ер З. Из колоды в 32 карты вынимают наугад три карты. Найдем вероятность того, что среди вынутых карт будет хотя бы один туз.

Эту задачу проще решить, используя понятие противоположного события и формулу Р(А) = 1 — Р(А).

Событие А — извлечен хотя бы один туз — означает, что число вынутых тузов будет не меньше чем 1, т. е. 1, 2 или З.

Гл ава

Событие А означает, что извлеченные из колоды три карты не содержат ни одного туза.

Вероятность того, что число вынутых тузов равно нулю, равна

Действительно, число равновозможных исходов равно Со, а число исходов, благоприятных для события А (О тузов), Вычислим Р(А):

                                   за                           28. 27 • 26

                             = 25!3! : 29!3! =                             32 . 31 . зо

                            7 - 9 - 13   819

                                  4 . 10 . 31 = 1240      0,66.

Отсюда

Р(А) = 1 - Р(А) 1 - 0,66 = 0,34.

Пример 4. В соревнованиях по бегу участвуют четыре спортсмена под номерами 1, 2, З и 4. Тренеры оценивают шансы занять первое место для спортсменов под номерами 1 и З как одинаковые, а для спортсменов под номерами 2 и 4 — вдвое меньше. Какова вероятность, что к финишу первым придет спортсмен под номером 1 или 4?

Пусть А, В, С и D соответственно события: «первым придет спортсмен под N2 1», «первым придет спортсмен под 2», «первым придет спортсмен под N2 З», «первым придет спортсмен ПОД NQ 4».

Положим Р(В) = P(D) = а. Тогда Р(А) = Р(С) = 2а. События А, В, С и D образуют полную систему. Значит,

1

т. е. 2а + а + 2а + а = 1. Отсюда а =

Применяя теорему о сложении вероятностей несовместных событий, найдем

Значит, вероятность того, что первым к финишу придет спорт1

смен под номером 1 или под номером 4, равна

1404.                 Бросают игральный кубик. Какова вероятность того, что выпадет:

а) 1 очко или 6 очков;

б) 5 очков или число очков, меньшее З?

1405.                 При стрельбе по мишени вероятность выбить 10 очков равна 0,2, а вероятность выбить 9 очков равна 0,5. Чему равна вероятность выбить не менее 9 очков?

1406.                 На каждой из четырех карточек написано по одной букве: о, р, с, т. Карточки положили на стол буквами вниз и перемешали. Затем взяли наугад одну карточку за другой и в том же порядке составили слово. Какова вероятность, что в результате оказалось слово:

а) сорт или трос;

б) не оказалось слова трос?

1407.                 Из колоды в 36 карт извлекают одну карту. Какова вероятность того, что эта карта будет:

а) королем пик или дамой треф;

б) дамой или валетом (любой масти);

в) картой червонной масти или тузом пик;

г) ни тузом, ни королем, ни дамой?

1408.                 В урне находится 36 шаров: 8 белых, 4 черных, 16 синих и 8 красных. Из урны извлекают один шар. Какова вероятность того, что этот шар окажется:

а) белым или черным;            в) не белым;

б) синим или красным;           г) не синим?

1409.                 В урне находится 11 шаров, из которых 7 белых и 4 цветных. Из урны извлекают один шар, фиксируют, цветной он или нет, затем шар возвращают в урну. После этого опять извлекают один шар. Какова вероятность того, что после двукратного извлечения оба шара окажутся цветными?

1410.                 В ящике находится 16 деталей, из которых 12 — стандартные. Найдите вероятность того, что среди двух извлеченных деталей есть хотя бы одна стандартная.

1411.                 В мешке находятся жетоны, номерами которых являются все трехзначные числа. Из мешка вынимают один жетон. Какова вероятность того, что его номер содержит хотя бы две одинаковые цифры?

Глава

Упражнения для повторения lxl - 2

1412.                 Постройте график функции у = ГЛ——.

1413.                 Решите неравенство

1414.                 Имеет ли предел последовательность (хп), если

( 1)^П п

62 ф

Умножение вероятностей

Рассмотрим пример. В урне находятся 6 жетонов с номерами от 1 до 6 включительно, т. е. номера жетонов в урне образуют множество М = {1, 2, З, 4, 5, 6}. Из урны вынимают один жетон. Обозначим буквой А событие, когда из урны вынимают жетон с номером, кратным 2. После этого жетон возвращают в урну. Затем из урны снова вынимают жетон. Пусть В — событие, означающее, что из урны изв.лечен жетон с номером, кратным З. Какова вероятность наступления события А и события В при этом испытании?

Для события А благоприятны исходы, образующие множество {2, 4, 6}, а для события В благоприятны исходы, составляющие множество {З, 6}. Поэтому Р(А) = б = Е, Р(В) = б = 3•

Событие В не зависит от события А, так как вероятность повторного извлечения жетона не влияет на то, какой жетон был вынут в первый раз (извлеченный в первый раз жетон был возвращен в урну).

Если после первого извлечения жетона из урны его не возвратят в урну, то вероятность вторичного извлечения жетона (событие В) будет иной, так как в урне уже не 6 жетонов, а 5. Если

1

в первый раз извлечен жетон, кратный З, то Р(В) = 5, если же

2 в первый раз извлекли жетон с номером, не кратным З, то Р(В) —

В этом случае вероятность события В зависит от события А, т. е. события А и В являются зависимыми.

В дальнейшем мы будем рассматривать независимые события. Два события называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.

Вернемся к рассмотренному примеру, когда жетон извлекали из урны и затем возвращали обратно.

Подсчитаем вероятность появления жетона с номером, кратным 2 и кратным З, в результате двукратного извлечения жетонов из урны с возвращением (событие С).

Событие С, состоящее в совместном появлении событий А и В, называют пересечением этих событий и обозначают С = А П В.

Множество равновозможных исходов при первом извлечении жетона — это множество М = {1, 2, З, 4, 5, 6}, а при втором извлечении жетона — то же множество М. Множество равновозможных исходов при двукратном извлечении жетонов — это множество пар (х, у), где буквой х обозначен номер жетона при первом его извлечении, а буквой у — при втором извлечении. Это множество записано в виде таблицы.

		1)	(4; 1)	(5;1)
	(2; 2)	2)	(4; 2)	(5; 2)
	(2; З)	(3;3)	(4; 3)	(5; 3)
4)	4)	4)	4)	(5; 4)
	(2; 5)	(3,	(4; 5)	(5; 5)
(1,	(2; 6)	(З,	(4; 6)	(5;6)

Всего равновозможных исходов 36.

Из этого числа равновозможных исходов благоприятными для события А П В будут З • 2 = 6 исходов. Это пары:

Значит, Р(А п

11

С другой стороны, Р(А) =Отсюда

Докажем, что вообще вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Пусть — число всех равновозможных исходов испытания, в которых событие А наступает или не наступает; пи — число исходов, благоприятных для события А;

 — число всех равновозможных исходов испытания, в которых событие В наступает или не наступает;

 — число благоприятных исходов для события В.

Гл ава

Общее число равновозможных исходов испытания равно п1п2, так как каждый из исходов, в которых событие А наступает или не наступает, может сочетаться с каждым из исходов, в которых событие В наступает или не наступает. Из этого числа исходов благоприятными для события А П В являются исходов. Действительно, каждый из пи исходов, благоприятных для события А, сочетается с каждым из исходов, благоприятных для события В. Поэтому

то - П1П2

      Значит,       п В) = Р(А) • Р(В).

Эта теорема допускает обобщение.

Несколько событий называют независимыми в совокупности, если каждое из них и любая комбинация остальных событий есть событие независимое. Так, если события 4, А А независимы в совокупности, то они попарно независимы.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

                        Р(А1 п А2 п ... п Ап) = Р(А1) • Р(А2) •             Р(Ап).

При мер 1. Монету бросают З раза подряд. Пусть А, В и С— события, означающие, что решка выпадает при первом, втором и третьем бросании. Найдем вероятность события А П В П С.

Каждое из двух событий А и В, А и С, В и С независимы, т. е. события А, В и С независимы в совокупности. Поэтому вероятность наступления события А П В П С равна произведению вероят-

1 ностей Р(А), Р(В) и Р(С). Так как Р(А) = Р(В) = Р(С)

Пример 2. Вероятность попадания в цель при стрельбе из первого орудия равна 0,8, а при стрель& из второго орудия равна 0,7. Найдем вероятность хотя бы одного попадания в цель, если каждое орудие сделало по одному выстрелу.

Пусть событие „41 означает, что цель поражена первым орудием, а событие „42 — цель поражена вторым орудием. Тогда 141 означает промах при стрельбе из первого орудия и А2 — промах при стрельбе из второго орудия. Отсюда имеем:

- = 0,2; р(Ћ2) = 1 - = 0,3.

События „41 и „42 независимые. Событие „41 П А 2 означает, что цель не поражена ни одним из двух орудий.

Следовательно, р(Ћ1 п 72) = р(Л) р(Ћ2) =            •           = 0,06.

Пусть событие А означает, что цель поражена хотя бы одним

орудием. Очевидно, что А и „41 П „42 — противоположные события. Поэтому

Р(А) = 1 - р(Ћ1 П 72) = 1 - 0,06 = 0,94.

1415.                 В урне находится 5 шаров: 2 белых и З черных. Из урны вынимают один шар. Фиксируют, белый он или черный. После этого шар возвращают в урну. Затем вновь вынимают шар. Какова вероятность того, что при двукратном извлечении шара из урны оба шара окажутся черными?

1416.                 Бросают два игральных кубика. Какова вероятность того, что на одном из них выпадет 2 очка, а на другом — нечетное число очков?

1417.                 Бросили игральный кубик и монету одновременно. Какова вероятность, что на монете выпадет орел, а на игральном кубике — четное число очков?

1418.                 Из трех станков, работающих в цехе, вероятность остановки за смену первого станка равна 0,2, второго 0,15 и третьего — 0,12. Какова вероятность того, что все три станка за смену не остановятся?

1419.                 В первой партии электролампочек находится 4 % бракованных, во второй партии — 5 % бракованных. Наугад берут две лампочки, одна — из первой партии, а вторая — из второй. Какова вероятность того, что:

а) обе лампочки окаэкутся исправными;

б) хотя бы одна из лампочек окажется исправной?

1420.                 Испытания на полигоне трех орудий показали: первое орудие поражает цель в 800 случаях из 1000, второе — в 750 случаях, а третье — в 600 случаях. Какова вероятность поразить цель, если каждое орудие совершит по одному выстрелу?

1421.                 Подбрасывают 4 игральных кубика. Какова вероятность того, что на каждом из них выпало число очков, кратное 2?

Гл ава

1422.                 В урне лежат 5 черных шаров, 4 красных и З белых. Последовательно вынимают три шара, причем каждый шар возвращают в урну перед тем, как вынимают следующий. Какова вероятность того, что первый шар окажется черным, второй — красным и третий — белым?

1423.                 Игральный кубик бросают три раза. Какова вероятность того, что при первом бросании выпадет нечетное число очков, при втором — четное число очков, а при третьем бросании — 6 очков?

          Упражнения для повторения

1424.                 Три целых числа составляют арифметическую прогрессию, первый член которой равен 1. Если ко второму члену прибавить З, а третий — возвести в квадрат, то получится геометрическая прогрессия. Найдите эти числа.

1425.                 Решите систему уравнений

2х — ly + 11 = 5.

1426.                 Решите уравнение:

-44+4-+4-                    Контрольные вопросы и задания

1.      Объясните, что называют частотой случайного события. Дайте определение вероятности. В чем состоит различие между статистическим и классическим понятиями вероятности?

2.      В каких случаях вероятности случайных событий складывают, в каких — перемножают? Приведите примеры.

--l—l-+-l---f..--l-- ф Дополнительные упражнения

к главе 7

К параграфу 21

1427. Из цифр О, 1, 2, З, 4, 5 составлены всевозможные шестизначные числа без повторения цифр. Сколько существует таких чисел?

432

tg² a — 3

1212. a) 1; 6) 

1 - 3tge a'

OraeTb1

2(1 + tg² a)

    ² ot . 1216. a) 1 tg p; 6) tg p.

1 — tg

1217. a) 2 —2; 6) —vi; B) —u; r) 2 —2. 1221. a = 3, b 12

24. 7 . —32 1225. 120.    119. -1 1 3 b = -12. 1224.

                                                        ï65' -ï65' ïïë•

1227. r) 2 tg a. 1228. a) —(cos x + sin x); 6) 2 sin a; B) cos ot; r) 1; A) cos ot. p 1

1231. a) tg—; 6) cœ 2 + B) — ctg 2a; r) 1 + sin 2a • 1234. a) —cos 4⁰ ;

1

6) sin² 12 ⁰ ; B) —cos 20 ⁰ ; r) cos 10 ⁰ . 1244. a) 2 1; 6) 1 1248. (0; 0), (—2; —4), (3; —1,5). 1250. a) cos 5 ⁰ ; 6) •.[5 cos 70⁰; B) cos 50⁰; r) sin 48 ⁰ .

1251. A) cos x; e) sin a; cos y; a) sin p. 1254.6) 4 cos 30⁰ — cos 30⁰ — — ;

             x — 45⁰    x + 45⁰

e) 4 sin  2   cos   2 . 1255. B) sin (60⁰ — x) sin (60⁰ + x); r) sin (x +

+ 45 ⁰ ) sin (x 45 ⁰ ). 1256. e) sin 2a + sin 2b; cos 2m + —cos 2n.

2

1258. a) ctg 2x; 6) —tg 2x; B) —ctg i; r) tg 1260. a) x = Itn, X + 21tn,

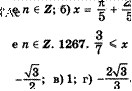21t

—n, x = 21tn, l'Ae n Z; B) x = —

2

< x < 1. 1274. a) (m + n)² ; 6) (x - y)² . 1277. a) 2

6) 1286. a) 203 ⁰ ; 6) 95 ⁰ ; B) -140⁰ ; r) 350⁰ . 1287. a) O;

1 — m2.

6) O; e) —1. 1289. a) ctg⁶ ot; 6) —sin² a; B) 2; r) sin a — cos a. 1291. a)

2

3m — rn³

6) . 1292. n² + 2, n(n² + 3). 1297. a) 1; B) 3; r) 2,5. 1303. a)

                             ctg ot ctg — 1. ctg a ctg p + 1 sin (a + P).

6)1307. a)                            6)      '

                                    ctg + ctg p    ctg p — ctg a sin (a — P)

cos (a — P) u sin ot sin 201. 1328. 1. 1329. cos B) 1321. a) 2 cos cos 2a; 6)

cos (ot + P)

1337. a) 120; 6) 5040. 1339. 24. 1342. 24. 1344. a) 28; 6) 42. 1345. 48 CIIOc06aMH. 1346. P6 • P4 — 1 = 17 279. 1348. 2664. 1349. = 25 npn n = 4;

6) a = 121 npn n = 5. 1350. a) x = 7; 6) x = 7. 1352. 1*1pu a < 1. 1353.

Ответы                                                                                                                           433

1355. = 720. 1356. 1680. 1359. 151 200. 1360.95 040. 1361. а) 280; 6) 720; в) 10. 1362. а)24; 6) 24; в) 12; г) 12. 1363. А} + А? + А? = 259. 1364. = З;

6. 1365. 1. 1366. 3 ¹² = 531 441. 1367. + 246; 6)8. 1370. С: = 15.

1371. = 45. 1372. - 12 = 54. 1373.  = 24 1374. с14 + +  15; 1 + с?- 27. 1376. а) 2 ⁸ ; 6) 2 ¹⁰ . 1377. с 10 + + + = 502. 1378. а) 6; 6) 4. 1379. = 220.

1380. а) п = 6; б) п = 7; в) х = 10; г) х = 11. 1381. 17 человек. 1382. п = 1; 2; з; 4; 5. 1386. 102. 1388. в) З; г) б. 1390. а) -; 6) З; в) 0,3; г) 0,7.

1391.

19 1392. а) 75; 6) 15; в) 0' 1393. с; :            1395.        1396. - 1397. 14 •

14 = зд• 1394. а) ИД; 1398. 10

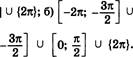
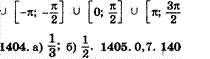1399. а) О; 6) О. 1400.        • 1403.               -7t] И [0; л] {2л}•, 6)

U {2n}; в) —2r,

23

                                                   —12'    24 • 1407. а) ТД;

16      - с:       19 1408. а) З; б) З; в) О; г) О• 1409. 121 • 1410. 1

1411. 0,28. 1413. [-0,3; 1). 1415.        1416.        1417.     1418. 0,5894.

1419. а) 0,912; 6) 0,998. 1420. 0,98. 1421.          1422.           1423.

1424. 1; 4; 7. 1425.(3•, 0), (3; -2). 1426. а) а; 6) 5. 1427. 600. 1428. 10!. 1429. 360. 1430. 13! • 5!. 1431. 6! • 10!. 1432. а) 120; 6) 240. 1433. 27.

1434. 64. 1435. 243. 1436. АК. 1437.           -        1438. а) 3Р5 = 360;

 Р, - 144. 1439. 1440. А? • А 4.³ 1440. 8!. 1441. СК. 1442. 210 чле-

                                                                          ¯                                          10                                              11

нов. 1443    = 15. 1444.        1445. ¯          - 0,04. 1446.       1447. 0,88.

100

                                                                         45.       с}о . с:        20

1449.б)

15

11

1452.       1453.                                        1454.    8. 1455. а)  =

434                                                                                                                           Ответы

     4      4      4                                        16

        п                         Тб5; б) Р(А1 U А2) = 165' в)                        и А2 U А3) = 55'

1456. 0,6. 1457. 0,95. 1458. 1 -

Огветы к задачам повышенной трудности

1459. У казани е. Приведите равенство к виду (а + b)(a + + с) = О. Аналогичным образом преобразуйте второе равенство. 1462. а) 1; 2;

. -11 + ИП У к а з а н и е. Разделите числитель и знамена-

           2                        2

тель каждой дроби на х; б) З; 3• 1463. а) У каз а н и е. Прибавьте к обе-

2х2 частюа уравнеютя по ² — 1'           У к а зан и е. Замените х

х + 5 на а и решите относительно х получившееся биквадратное урав-

1            1             1 нение. 1464. а) х = ab + ас + bc, если

1    1             1 любое число, если  = О. У к аз ан и е. Перенесите

все члены уравнения в левую часть и сгруппируйте попарно; б) х = а + b + с, 1 1 1  1 1 1 если ас b + C О; х — любое число, если — ас b + C

Указани е. Перенесите все члены уравнения в левую часть и представьте ее в виде суммы трех слагаемых. 1465. У к а зан и е. Представьте уравнение в виде квадратного и преобразуйте его дискриминант.

1466. а) (-4; 1 ; 6) 1]. 1467. (-6; 6); (-6; 2). 1468. а (-3; 6). 1469. а) (2; 2); 6) (1; 1), (-1; -1). 1470. (-45; 4). 1471. а) (2; 1), (-1; -2);

6) (2; 1), (1; 2), (-3; 0), (0; -3), (1; -2), (-2; 1). 1472. а)

(6- Л6;2-Л6). У к аз а н и е. Обозначьте х — у буквой и восполь-

зуйтесь монотонностью функции f(z) = 2⁵ + 62⁸ ; б) (О; О); (2 + ф; 2 + ф).

Ук аз ан и е. Вычитая из первого уравнения второе, получите уравнение (х — + ху + у² — 2х — 2у + 2) = О и докажите, что второй множитель в левой части этого уравнения принимает при любых у положительные значения. 1473. Не су:цествует. 1474. а) (6; —1); (—6; 1); б) (6; 6); (1,56 — 1,5; — 1,5); (—1,56 + 1,5; 1,5% — 1,5). Указани е. При-

ведите уравнение к целому виду и введите переменные и = х + у, v = ху.