
Дополнительные задания для самостоятельного выполнения
Самостоятельная работа
1. Вычислить значение бинома:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
![]()
ОТВЕТЫ:
1) ![]()
2) ![]()
3) ![]() 4)
4) ![]()
№1. Вычислите степени бинома:
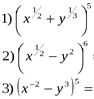
Ответы:
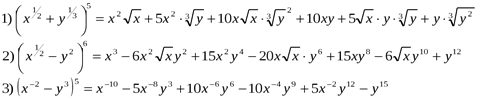
№2. Доказать, что значение выражения ![]() , где n –
натуральное число, делится на 16 без остатка.
, где n –
натуральное число, делится на 16 без остатка.
Решение.
Представим первое слагаемое выражение как ![]() и
воспользуемся формулой бинома Ньютона:
и
воспользуемся формулой бинома Ньютона:

Практическая работа № 14. Бином Ньютона
Вопросы к работе
1. Прочитать формулу бинома Ньютона.
2. Как строится треугольник Паскаля для нахождения коэффициентов бинома Ньютона?
3. По какой формуле найти s-й член бинома Ньютона?
Образцы решения заданий
Пример
1. Написать разложение по формуле бинома Ньютона и упростить ![]() .
.
Решение:
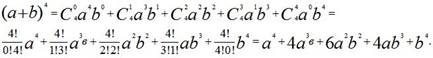
Пример
2. Найти алгебраическую сумму коэффициентов многочлена относительно x,
получаемого в разложении бинома Ньютона ![]() .
.
Решение.
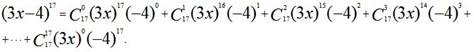
Это равенство истинно при любом значении х.
При x = 1
левая часть равна ![]() , а в правой
части получаем алгебраическую сумму коэффициентов:
, а в правой
части получаем алгебраическую сумму коэффициентов: 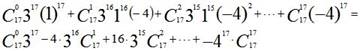
Следовательно, алгебраическая сумма коэффициентов данного многочлена равна –1.
Пример 3. Найти 13-й член разложения бинома
![]() .
.
Решение. Согласно формуле общего члена разложения бинома,
![]()
Пример
4. Найти номер члена разложения бинома ![]() , не
содержащего х.
, не
содержащего х.
Решение. Для общего члена
разложения имеем
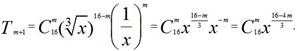
Член
разложения не зависит от x; это значит, что показатель
степени x равен 0, только тогда, когда![]() , 16
– 4m = 0, m = 4.
, 16
– 4m = 0, m = 4.
Итак, пятый член данного разложения не зависит от х.
Упражнения
1. Написать разложение по формуле бинома Ньютона и упростить:
а) ![]() ;
Ответ:
;
Ответ: ![]() .
.
б) ![]() ; Ответ:
; Ответ:![]() .
.
в)
![]() ;
Ответ:
;
Ответ: ![]() .
.
2. Найти пятый и девятый член разложения:
а)
![]() , б)
, б) ![]() .
Ответ:
.
Ответ: ![]() .
.
3. Найти два средних члена
разложения ![]() .
Ответ:
.
Ответ: ![]() .
.
4.
Найти в биномиальном разложении 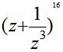 член, не
содержащий z. (Ответ:
член, не
содержащий z. (Ответ: ![]() ).
).
5. Используя треугольник Паскаля найти коэффициенты разложения:
а) ![]() ,
, ![]() .
.
Индивидуальные задания
1. Разложить по формуле бинома Ньютона и упростить. Коэффициенты разложения найти, используя треугольник Паскаля:
1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
;
4) ![]() ;
5)
;
5) ![]() ;
6)
;
6) ![]() ;
;
7) ![]() ;
8)
;
8) ![]() ;
9)
;
9)![]() ;
;
10) ![]()
2. Найти два средних члена разложения:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4)![]() ;
5)
;
5) ![]() ;
;
6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ;
10)
;
10) ![]() .
.
Задание для самоконтроля
1. Найти сумму:
1) ![]() (Ответ:
(Ответ: ![]() );
);
2)
![]() (Ответ: 0).
(Ответ: 0).
2. Доказать справедливость равенства: ![]() .
.
12. Треугольник Паскаля.
Для вычисления биномиальных коэффициентов используется специальная таблица.
Таблица 2
Вычисление биномиальных коэффициентов
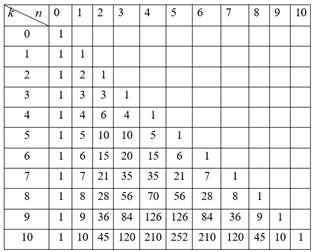
Биномиальные коэффициенты удобно выстроить в Треугольник Паскаля – равнобедренный треугольник, обладающий следующими закономерностями:
1)
в ![]() строке
треугольника записываются биномиальные коэффициенты
строке
треугольника записываются биномиальные коэффициенты ![]() -й степени
бинома;
-й степени
бинома;
2)
число ![]() располагается
в
располагается
в ![]() строке
на
строке
на ![]() месте;
месте;
3) боковые стороны треугольника состоят только из единиц;
4) каждое внутреннее число строки равно сумме двух последовательных чисел предыдущей строки, стоящих над ним слева и справа.
На
рисунке 7 представлен треугольник Паскаля, выстроенный для коэффициентов
разложения бинома ![]() -й степени.
-й степени.
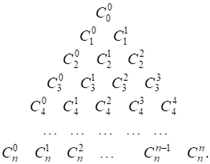
Рис. 1
Треугольник Паскаля
Например,
при ![]() треугольник
Паскаля имеет вид:
треугольник
Паскаля имеет вид:
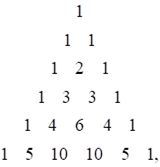
Значит, ![]() .
.
Задачи и упражнения.
12.1. Найдите
разложение бинома![]() .
.
12.2. Докажите,
что ![]() .
.
12.3. Проверьте выполнение равенства задачи 3.27 для 8 и 10 строк треугольника Паскаля.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.