
готовимся к гп
ЪЕллекх
клпсс
Г.Д. Карташёва
Алгебра
8 класс
ПРАКТИКУМ
Москва
«Интеллект-Центр»
2013
![]()
ББК 22.1я721
К27
Карташёва, Г. Д.
К27 Алгебра. 8 класс. Практикум. Готовимся к ГИА • [учебное пособие] / Г.Д. Карташёва. — Москва: Интеллект-Центр, 2013. — 96 с.
ISBN 978-5-00026-006-7
Данное пособие представляет собой практикум по решению задач, предназначенных для закрепления и систематизации знаний учащимися по алгебре за курс 8 класса. Пособие ориентировано на повышение уровня общей математической подготовки школьников. В книге дан краткий теоретический материал, который ученик должен знать после изучения темы, необходимый для выполнения упражнений, приведены опорные задачи с решениями, а также задания базового и повышенного уровня сложности для самостоятельного решения учащимися.
В конце темы даны тесты для самоконтроля и диагностики проблем в знаниях учащихся и их последующей коррекции.
Пособие написано в соответствии с программой курса алгебры 8 класса, но больше ориентировано на учебник «Алгебра, 8» (авторы — Ю. Н. Макарычева и др.). Оно также может быть использовано и при работе по другим учебникам.
Пособие адресовано ученикам 8 класса, их родителям, учителям и методистам.
удк![]()
ББК22.1я721
Генеральный директор издательства «Интеллект-Центр»
М. Б. Миндюк
Редактор Д. П. Локтионов
Художественный редактор Е. Ю. Воробьева
Подписано в печать 18.06.2013. Формат 60х84/8.
Бумага офсетная. Печать офсетная. Усл. печ. л. 12,0. Тираж 5000 экз.
Издательство «Интеллект- Центр»
125445, Москва, ул. Смольная, д. 24А
ISBN 978-5-00026-006-7 О «Интеллект-Центр», 2013
О Г.Д. Карташёва, 2012
СОДЕРЖАНИЕ
Предисловие![]()
Повторение изученного в 7
классе![]()
Проверочная
работа![]()
1. Рациональные дроби![]()
1. Рациональные
дроби и их свойства![]()
2. Сумма
и разность дробей![]()
З. Произведение и частное дробей![]()
4.
Деление дробей![]()
5.
Преобразование рациональных выражений![]()
6. Функция у =— и ее график![]()
Тест 1.
Рациональные дроби![]()
II. Квадратные корни![]()
1. Рациональные числа![]()
2. Иррациональные числа![]()
З. Квадратные корни. Арифметический квадратный корень![]()
4.
Уравнение х = а![]()
5. Функция у = 47 и ее график![]()
Тест 2. Арифметический квадратный корень![]()
6.
Свойства арифметического квадратного корня![]()
7.
Вынесение множителя за знак корня. Внесение множителя под знак корня![]()
8. Преобразование выражений,
содержащих квадратные корни ![]() Тест З. Квадратные корни
Тест З. Квадратные корни![]()
III.
Квадратные уравнения![]()
1. Неполные
квадратные уравнения![]()
2. Решение
квадратного уравнения по формулам![]()
З. Решение задач с помощью квадратных уравнений![]()
4. Теорема Виета![]()
Тест 4. Квадратные уравнения![]()
5, Дробные рациональные уравнения![]()
6. Решение задач с помощью рациональных уравнений ![]() Тест 5.
Дробные рациональные уравнения
Тест 5.
Дробные рациональные уравнения![]()
IV.
Неравенства![]()
1.
Числовые неравенства![]()
2.
Свойства числовых неравенств![]()
З. Сложение и умножение числовых неравенств![]()
4. Числовые промежутки![]()
5.
Решение неравенств с одной переменной![]()
6.
Решение систем неравенств с одной переменной![]()
Тест 6.
Неравенства![]()
V. Степень с
целым показателем. Элементы статистики![]()
1.
Определение степени с целым отрицательным показателем![]()
2.
Свойства степени с целым показателем![]()
З. Стандартный вид числа![]()
Тест 7. Степень с целым показателем. Стандартный вид числа ..
.![]()
4.
Элементы статистики![]()
5. Функции у = х- и у = х- и их свойства![]()
6.
Дисперсия и среднее квадратичное отклонение![]()
Тест 8. Итоговый тест![]()
Ответы ![]() ПРЕДИСЛОВИЕ
ПРЕДИСЛОВИЕ
Данное пособие содержит задачи по основным темам курса алгебры 8 класса и предназначено для закрепления и систематизации знаний учащимися, выработки прочных навыков по всем темам. По каждой теме дается:
опорный теоретический материал; образцы решения типовых задач по теме; задания для самоконтроля.
В конце каждой темы приводится тест, который по форме соответствует заданиям, использующимся в настоящее время как при государственной итоговой аттестации за основную школу, так и в едином государственном экзамене.
Тесты могут использоваться как учениками для самопроверки, так и учителями для контроля знаний учащихся всего масса.
Тренировочные упражнения даны на базовом и повышенном уровне для учащихся, которые хотят знать больше.
В конце даны ответы и комментарии к ним.
Пособие
ориентировано на учебник «Алгебра 8» авторов Ю.Н. Макарычева, Н.Г. Миндюк, К.И.
Нешкова, С.Б. Суворовой, а также может быть использовано при работе по другим
учебникам алгебры для 8 класса.
ПОВТОРЕНИЕ ИЗУЧЕННОГО В 7 КЛАССЕ
Для изучения первой темы 8 класса повторите тему «Выражения и их преобразования» за курс 7 класса (смотри учебник 8 класса раздел «Сведения из курса алгебры 7 класса»). Выполните после этого задания.
1. Какие из выражений:
1) 5а2х ; 5) !аз х 2 —4;
2)
—3a2 b3
—8a2b5 ; ![]() 5. 6) х2 —28х+4х
5. 6) х2 —28х+4х![]()
являются:
а) одночленами;
б) многочленами?
2. Укажите степень одночлена:
1) —603х2 , 2) —a3b4 , 4) у5.
З. Какие из многочленов, являются многочленами стандартного вида:
1) 2х5у+8хЗу—5х5у ;
2
2) —2х уз +7ху2 +3ху ;
З) —a2 b—3ab2 ?
Перед выполнением следующего задания вспомните правило раскрытия скобок, перед которыми стоит знак «+» или «—».
4. Найдите сумму или разность следующих многочленов:
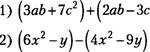 2), 3) (зу
2 -0+1)—(5у—2); 4) (-7х 2
2), 3) (зу
2 -0+1)—(5у—2); 4) (-7х 2 ![]()
5. Составьте:
а) сумму многочленов
6х —5х —8 и —2х —8х +3х+5 и преобразуйте ее
в многочлен стандартного вида; ![]()
б) разность многочленов
5у —10 и 7у —Зу+5 и преобразуйте ее в многочлен стандартного вида.
6. Решите уравнение:
а) ![]() = 17 ;
= 17 ;
6) ![]() = -6,7 .
= -6,7 .
7. Преобразуйте произведение в многочлен:
а) —2a3 (4ab2 —b3 +1) ;
6) (5х2![]()
8. Для выполнения этого задания повторите формулы сокращенного умножения. Преобразуйте выражение в многочлен стандартного вида:
|
1) (3X+2)2 , 6) (-2х+Зу)З , |
11) |
|
2 2) (бу2 -7) , 7) (a+b)2 —2ab ; |
12) (х2 +6)(х2 —6) ; |
|
3) —a-2b
|
13) (0,7х2 |
|
4) (—Х+5)2 , 9) 9. Разложите многочлен на множители. 1 ) Вынесением общего множителя за скобки: а)
3х2у—6хуЗ. б) —24х3у5 +36х2
у2 г) a(a—b)+4(a—b); д) c2 (b—5)—6(5—b) . |
14) (5х2
|
2) Способом группировки:
а) 5х—5у—ах+ау ;
б) ab—4b+ay—4y ;
в) 3ху+15у—Зх—15;
г) 60a+8ab—30a —4ab .
|
З) С помощью формул сокращенного умножения: |
|
|
|
|
а) а2 —36х2 в) х8 —81; |
д)
(a—b)2 |
|
ж) хз +27. |
|
б) аи —25
; 4) С применением нескольких способов: |
е) 8—b3 , |
|
|
|
а) a(2b—c)+4b2 —8 , |
—а —х—а; |
|
д) 16—8 +а 2 —8а. |
|
б) х2 —2ха+а2 —b2 ; 10. Решите уравнение: |
—а2 + 2ab—b2
|
|
|
1) х2 -2х=о; 3) 16х-х о 5)
(х+1)х![]()
2) уз-У=О; 4) 6х4 —24х2
= О; ![]() 2 =25у-25.
2 =25у-25.
ПРОВЕРОЧНАЯ РАБОТА
Вариант 1
Укажите степень одночлена
а) блу ; 6)
-0,8х2 у; в) ![]()
|
а |
б |
в |
|
|
|
|
|
|
|
1) 3a2 6a2 b; 2) 7х6у 4 3) (3ab 2 )2 • (—2a3 b)3 ; |
4) ——bc1 2 —b2 3 c5 2 |
|
|
З. Приведите подобные члены многочлена: 1) —а4 +3аз —5а4 +3а2 —2аз —5а2. 2) 3+3х5 -4х3 -8х5 +4х3 -2у5 -9 ; 2 З) 9х у —6ху2 —4х2у +3х2у —Злу2. 4) 4ab3 +9a2b2 —ab3 —5a2b2 —3a2b2 —5 . 4. Преобразуйте в многочлен стандартного вида: |
|
|
|
|
в) (3х2 |
(—2х 2 +6) ; |
|
б) (b2 —b+7)—(b2 5. Выполните умножение: |
г) (9т з |
|
![]() а) 3а(2а2 —8а—4) ;
а) 3а(2а2 —8а—4) ;
б) —4х2 (3х2 —3х—2)![]() .
.
|
6. Выполните умножение: |
|
|
а) (а2 +b)(a—b2 ); б) (9—х2 )(х2+9); 7. Разложите многочлен на множители: |
|
|
1) ах+ау+7х+7у; 3) 48 —9; |
5) а 2 +2ab+b2 2 |
![]() 4) (a+2b)2 -(a-2b)2.
4) (a+2b)2 -(a-2b)2.
![]() 8. Решите уравнение:
8. Решите уравнение:
2 12 З
Вариант 2
Укажите степень одночлена
|
а) —5х 2у ; |
б) 0,8х3у2 |
в) |
a2b2 . 5 |
г) |
|||||
|
а |
б |
В |
|
|
||||
|
|
|
|
|
|
||||
|
2. Какой из одночленов дан в стандартном виде |
|
|
з З. Приведите подобные члены многочлена: 1) 2а4 —4аз —7а 4 +5а2 —а з +6а2 . 2) 7+4у5 -4х3 +7у5 -2х3 -10; З) —9ху2
+5х2у —6ху2 —2х2 у+8ху2 |
2 |
![]()
![]()
![]() [1]——a2 2 —Ка З) —6х3у5 1)
(3хуЗ )2 •(—5х4 у2 )З ,
2) b.
[1]——a2 2 —Ка З) —6х3у5 1)
(3хуЗ )2 •(—5х4 у2 )З ,
2) b. ![]()
4) ![]() —a2b+8a%3 —2a 2b2
—4 .
—a2b+8a%3 —2a 2b2
—4 .
|
4. Преобразуйте в многочлен стандартного вида: |
|
|
а) (3х —4х) ; |
в) (х +4) + (—3х2 + х) ; |
|
б) (—4а2 —5а+2)—(а2 +а—5) ; 5. Выполните умножение: |
г) (a2b2
+а 2 |
|
а) -5а(-2а2 -7а+4) ; |
в) (—у2 |
|
6) 4х2 (-зх+5х2 -2) ; 6. Выполните умножение: |
г) (—2х 2 у
2 —х 2 +у2 |
![]()
|
б) (5—у2 )(у2 +5) ; 7. Разложите на множители многочлен: |
г) 5х •(4 +х)2 . |
|
|
|
1) 8ab+8b+7a+7 ; 3) 258-16; |
|
5) 4х2 —а |
—2ab—b2 . |
8. Решите уравнение:
1) ![]() = 24 ;
= 24 ;
5у+4 6—3у _ 4у—1
2) ![]()
14 21 7
![]()
1. РАЦИОЊИЬНЫЕ ДРОБИ
![]() 1. Рациональные дроби и их
свойства
1. Рациональные дроби и их
свойства ![]()
Какие из выражений:
2
![]() х З)
(а+4)(а—5) ; 5)
х З)
(а+4)(а—5) ; 5) ![]()
2) 4) (х—4): (х—9) ;
6
являются целыми, какие — дробными?
Укажите допустимые значения переменной в этих выражениях.
12. Из рациональных выражений:
![]() 7
7
1) 3х2
-7ху•, З) а(а—З)![]()
4а
![]() а
а
2)![]()
выпишите те, которые являются: а) целыми выражениями;
б) дробными выражениями.
13. ![]() Укажите
допустимые значения переменной в выражении:
Укажите
допустимые значения переменной в выражении:
4х 10 а
а)![]() в)
в)![]() д)
д)![]()
х
9
б) ![]() г)
г) ![]()
16-b2 1х1—4
14. Найдите значения выражений при заданных значениях входящих в них букв. Заполните таблицу
|
х |
|
-6 |
з |
-2 |
- 1 |
4 |
12 |
1 2 |
1 З |
|
|
36 х |
|
|
|
|
|
|
|
|
|
|
а)
|
х |
0 |
1 |
2 |
з |
5 |
1 |
8 |
9 |
10 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(6—х) |
6)
![]() 8 25 27 63 72 15. а)
Сократите дробь:
8 25 27 63 72 15. а)
Сократите дробь:![]()
![]() 1 5 7 9 З б)
Приведите дроби к знаменателю 48:
1 5 7 9 З б)
Приведите дроби к знаменателю 48:![]()
2612 8 4
16. Будут ли равны дроби:
![]() З З(а-2) а—4 (а—4)(а+5)
З З(а-2) а—4 (а—4)(а+5)
![]() а—2 а—З (а —3)(а+5)
а—2 а—З (а —3)(а+5)
17. Можно ли поставить знак
равенства между выражениями: а2 —16 (а—4)(а+4) а)![]()
а 2 —25 ' (а+5)(а—5) ' а—5
1) При каких значениях а эти равенства будут верными, а при каких нет? а2 —16
2) Как называется замена выражения на а+4 ?
З) Что такое тождественное преобразование выражения?
4) Какие тождественные преобразования выражений вы знаете?
5) Является сокращение дробей одним из примеров тождественных преобразований?
18. Сократите дробь:
8а с а(6—З)
а)в) '
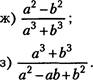
3 9х2 + 45ху
7х у
б)г)
21х2у х+5у
19. Найдите значение дроби:
![]() 158 +10ab
158 +10ab
ЗаЬ + 2b
х2 —6ху+9у
б) прих——02 , , у --о,б.
4х2 —12ху
20.
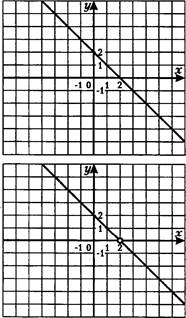 |
|||||
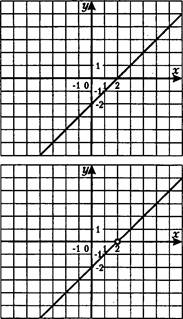 |
|||||
Рис. 1
21. Упростите выражение:
|
а) |
(-а-2)2 в) |
а—2 д) |
|
2-а |
|
(2—а)2 |
|
(а-2)2 б) |
г) |
(а -4- 2)2 е) |
|
2-а 22. Сократите дробь: |
(2—а)2 |
2 |
![]() (За
+ 3b)2 (2c-6d)2 (3х
— бу)2
(За
+ 3b)2 (2c-6d)2 (3х
— бу)2
а) б) ![]() в) г)
в) г)
c—3d 5х-1Оу (15х-5у)
23. Докажите, что значение дроби не зависит от п,где п — натуральное число:
![]() 5 +5 —571
5 +5 —571
а)
![]() б)
б)
5П+2 —9
2. Сумма и разность дробей
Сложение и вычитание дробей с одинаковыми знаменателями
![]() a—b
a—b
Пример 1. Выполним сложение дробей
ба-Љ 9а-ЗЬ ба-7Ь+9а-ЗЬ 15a-10b 5(За — 2b) За-2Ь
15ab 15ab 15ab 15аЬ 15ab ЗаЬ
Пример 2. Выполним вычитание дробей
![]()
24. Выполните сложение или вычитание:
![]()
![]() 2За— х 2х
2За— х 2х
14а
б)в)г)
5 5 ' х х 8 8 ' b b
25. Представьте в виде дроби:
|
b b-2a За За |
За—Ь 2a+6b a—5b в) |
|
ис-35 5-2с б) |
2х—3у 11у —4х 2х+8у г) |
|
бс бс |
(ху 4ху 4ху |
![]() а а 2
а а 2
26.
Упростите выражение, используя тождества: — ![]() Ь —b
Ь —b
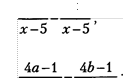
в)
![]() д) 2
'
д) 2
'
а 6 13a—6b 11a+4b
6) 2 ' ![]() а—З З—а е)
а—З З—а е)
а2 —b2 а2 —b
|
27. Преобразуйте выражение: |
|
|
а2 36 а) |
2 х 5(2х-5) в) |
|
Х2 +36 12х б) |
81— 2ab 2ab—a2 г) |
|
28. Используя тождество |
= —+— , представьте дробь в виде суммы дробей: |
|
а) х |
|
29. Представьте дробь в виде суммы двучлена и дроби. Выясните, при каких натуральных п данная дробь принимает натуральные значения.
Сложение и вычитание дробей с разными знаменателями
а с ad bc ad ± bc
|
Ь d¯ bd ¯ bd |
bd |
|
5 з 5.зх .3у2 |
15х+3у2 |
![]()
![]() Выполняется по правилу —±—
Выполняется по правилу —±—![]()
Пример
1. 2х3у4 6х4у2 6х4у4 6х4уа 6х4у4
![]()
Пример 2. ![]()
30. Представьте в виде дроби:
![]()
![]()
![]() 2ху
—1 Зу — х
2ху
—1 Зу — х
в) 2 З ![]() д) а—З—--—
д) а—З—--— ![]() 6х
6х
|
b2 а б) |
|
2а2 —1 е) |
а
31. Преобразуйте в дробь выражение:
|
|
в) |
|
|
х—1
32. Упростите выражение: |
г) |
|
|
а) |
|
|
|
х —2х х2—4' |
|
20 + З |
а—Ь а
б)![]()
33. Выполните действия:
![]() х —4х 2х
х —4х 2х
а) ![]()
х2 —16 х—4
б) ![]() аз —8
аз —8
З. Произведение и частное дробей
Умножение дробей. Возведение дроби в степень
Правило: 1)
Ь d bd
2)![]()
36х6 у2 36х6 •у 2 _ 4
Пример: 1) ![]() у 9х6 у8
• 9х6 у
у 9х6 у8
• 9х6 у
2)
 2ху
2ху
За
![]() 3)
3)
34. Выполните действие:
![]()
![]() 16х4 52 b 2
16х4 52 b 2
а) в)д) —a
25 4х
![]()
![]() 72х 2,5у5 т—п Зтп
72х 2,5у5 т—п Зтп
г) ![]()
х—З 25у6 16х4
35. Выполните умножение:
|
4 |
а |
|
а) (ба-ЗОЬ). |
2ху 2 2 |
|
(х-2)2 36. Представьте в виде дроби: |
х — бху + 9у |
|
2 ab2 а +а5 а) |
8-16 5х в) |
|
а+а a2b3 |
10ar За +12 |
|
б) |
Ь—а 4a2 b г) |
![]()
![]()
![]() г)
г)
2
![]() а2
—b2
а2
—b2

37. Выполните деление:
![]() 1 От
15т2 11х 2
1 От
15т2 11х 2
в) ——: (44ху) ; д) бп 8 8у2 х2 —6х+9 х2 —3х
28 14х
![]()
![]() 6)
6)![]() г) е)
г) е)![]()
![]() 9х3
зуа 2 +4 а 4 —16
9х3
зуа 2 +4 а 4 —16
38. Представьте выражение в виде дроби и сократите ее:
а) (х +4у) : (х2 —16у2 ) ; в) (х2 —25у2 ) : (х2 +10ху +25у2 ) ;
б) (а2 —8ab+16b2 ) : (а2-168); г) (a—4b)2 : (32b2 —28).
39. Упростите выражение:
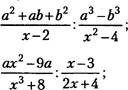 2т
+ бп
2т
+ бпа)г) : (Т2 +6тп+9п2 ); пт
6)д)
![]()
![]() 4+4а+а • 2х+ах аз +7b 49 —а2
4+4а+а • 2х+ах аз +7b 49 —а2
в) ![]()
![]() 9b2 а
—1 а -4-а+1
9b2 а
—1 а -4-а+1
15
5. Преобразование рациональных выражений
Перед выполнением упражнений надо внимательно прочитать соответствующий пункт учебника.
40. Выполните действия:
![]()
![]() а)в)
а)в)
Ь
![]() х ху—
у . х+З х—З б)
х ху—
у . х+З х—З б) ![]() г)
г) ![]() х—1 х
х—1 х ![]() х—З х+З
х—З х+З
41. Упростите выражение:
2
![]()
![]()
![]() Ь—а4х2
—9 2х—3 4—х
Ь—а4х2
—9 2х—3 4—х
а) в) 2
![]() 3х-1 1—3х
3х-1 1—3х
За1 — 6х + 9х
![]() 2ab
а2 —b2
2ab
а2 —b2![]() 4—4b+b2
4—4b+b2
да а+2 4
42. а) Являются ли тождественно равными
выражения![]()
а2 —4 2а а—2
![]() 2х х2
—4
2х х2
—4
б) Упростите выражение х—— • 2 и
найдите его значение при х — — 1 З![]()
х
6. Функция у =— и её график
х
График называется гипе лой, которая состоит из двух ветвей.
При к > 0 гипербола расположена в I и III четвертях.
При к < 0 гипербола расположена во II и IV четвертях координатной плоскости.
16
43. Функция задана
формулой у =![]()
х
Заполните таблицу и постройте график функции:
|
х |
1 |
2 |
4 |
8 |
12 |
16 |
- 1 |
-2 |
-4 |
-8 |
-12 |
— 16 |
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
10 44. Обратная пропорциональность задана формулой у = Найдите значение функции,
х соответствующее значению аргумента, равному 0,1; - 0,02, 100. Найдите значение аргумента, соответствующее значению функции, равному 0,05; 10; — 20.
45. Задайте формулой обратную пропорциональность, зная, что ее график проходит через точку:
а)
А(8; 1,25); ![]() в) 500; 0,002).
в) 500; 0,002).
46. Известно, что график функции у = проходит через точку А(— 4; -0,25). Проходит ли это график через точку:
а) 8; - 0,125); 6) С(50; - 0,02); в) 40; - 0,05)?
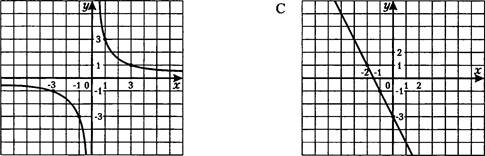
47. На рисунке построены графики функций. Задайте эти функции формулами.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
-2 -1 0 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2

48. Постройте график функции:
32
(х+1)2 -(х-1)2 '
16
(2 —х)2 —(2+
х+4
Х2 +8х+16
Тест 1. Рациональные дроби
Вариант![]()
Часть![]()
54х7
У![]()
1.
Произведение дробей ![]() можно
заменить дробью у 9х
можно
заменить дробью у 9х
1)
![]() 2)
2)![]() 3)
3)![]()
2. Частное
(Зба Ь![]() равно дроби
равно дроби
9b2 зь8 зьб
1)
![]() 2)
2)![]() 3)
3)![]()
7х2у![]()
![]()
![]() З.
Выполните действие
З.
Выполните действие ![]() (14х4у4
(14х4у4 ![]()
49х2
3)![]()
![]() 8х49х
8х49х
![]() а2 —b2
а2 —b2
4. Произведениетождественно равно
% +20b
|
а—Ь 2) |
3) |
|
5а + 5b |
5(a—b) |
5.
Функция задана формулой у =![]()
Какие из данных точек А(— 4; 2), В(4; 2), С(— 8; — 1), D(— 2; 4) принадлежат графику функции?
6.
Выполните действие ![]()
Ответ:
![]()
у—х 16х 16х
7.
![]() Упростите выражение
Упростите выражение
Х¯У У
Ответ:
![]()
Часть 2
К заданиям 8— 10 запишите решение.
12х 8х-25 1
8.
Упростите выражение 4х— и найдите его значение при х =![]()
х—2 З
9.
Постройте график
функции у =![]()
Х +2х+1
10. График функции у = — проходит через точу А. Найдите к, если А(к2;- 0,25)
х
Вариант 2
Часть 1
638![]()
1. Частное дробей можно заменить дробью
9а 9а 12
1) 2)![]() 3)
3)![]()
2. Произведение —14х2у равно
42у4
3х
1)
2)![]() 3)
3)![]()
зу
5 ![]()
З. Выполните действие 64х у![]()
4х 4уз
2)
![]() 3)
3)![]()
4. Произведение ![]() тождественно равно дроби
тождественно равно дроби
а—2 а—2
1) 2) 3) ![]()
За — 3b
-15
5.
Функция задана
формулой у = ![]()
Какие из данных точек А(З; — 5), В(— ![]() 1; 15)
принадлежат графику функции?
1; 15)
принадлежат графику функции?
6. Выполните
действие ![]()
Ответ:
![]()
а2 -Fb2 4ab
7. Упростите выражение
2ab ![]()
Ответ:
Часть 2
К
заданиям 8—10 запишите решение. ![]()
5х-16 5х
8. Упростите выражение х— и найдите его значение при х- - 0,2. х—З х—З
6х—6
9. Постройте график функции у =
![]()
10. График
функции у проходит через точку В. Найдите к, если В![]()
9
Н. КВАДРАТНЫЕ КОРНИ
Действительные числа
1. Рациональные числа
49. Верно ли,
а) —6Е М; —6е Z; —6е Q; 6) 6,76 М; 6,7Е 2;
в) 30€ М; ЗОЕ
z;30E![]()
50. Представьте в виде отношения целого числа к натуральному несколькими способами числа:
4 З
![]() 2- 0,7;-19; О.
2- 0,7;-19; О.
51. Представьте в виде дроби с наименьшим натуральным знаменателем числа:
1 ![]() 4
4
35; - 43; 5,3; -0,9; 14 ¯ ;
6 9
52. Представьте в виде бесконечной десятичной дроби число:
2 З 4 7
в)![]() д)
д)![]() ж) —
18;
ж) —
18; ![]()
3'1540 5 19 5 5 б)![]() г)
г)![]() е)
12,27;
е)
12,27;
53. Сравните рациональные числа:
7
|
а) 2,014 и 2,104; |
в) -3,27 и-з,47; |
д)- 1,176и -1— |
|
6) - 0,003 и 0,001; |
г) - и о,375; |
|
13 14
54. Укажите какое-либо число, которое:
1 а) больше — , но меньше — ![]() 8 '
8 '
![]() 1 1 б) больше но меньше — 10 ' 9
1 1 б) больше но меньше — 10 ' 9
2. Иррационаљные числа
55. Приведите пример:
а) рационального числа;
б) иррационального числа.
56. Верно ли,
а) каждое иррациональное число является действительным;
б) каждое действительное число является рациональным;
в) каждое натуральное число является рациональным;
г) любая бесконечная десятичная дробь является действительным числом?
57. Среди чисел:
1
0; 0,57;![]() 516;
516; ![]()
укажите рациональные и иррациональные.
58. Какое из чисел больше:
З
|
а) 2,(57) или 2,57; |
в) 1— или 1,4286; |
|
|
б) — 5,4(8) или — 5,48; |
г) З— и 3,142; |
|
59. Найдите расстояние между точками А и В координатной прямой,если:
![]()
60. Расположите в порядке возрастания числа:
5,62; —
4,75..., — 4,64![]()
61. Найдите приближенное значение выражения а + Ь, где а — 2,0549.. и Ь - 3,0620..., округлив предварительно а и Ь:
а) до десятых; б) до сотых; в) до тысячных.
62. Найдите
приближенное значение выражения а - Ь, где а — 58,789... и Ь - 45,234...,
округлив ![]() предварительно а и Ь:
предварительно а и Ь:
а) до десятых; б) до сотых.
З. Квадратные котм. Арифметический квадратный корень
Определение 1. Квадратным корнем из числа а называется число, квадрат которого равен а.
Определение 2. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
Обозначение арифметического квадратного корня из числа а: а
![]()
Га=ь, b2 =а, b>0, aZ0. (Гау=а, 00.
63. Докажите,
а) число 7 есть арифметический квадратный корень из 49;
б) число 0,5 есть арифметический квадратный корень из 0,25;
в) число — 6 не является арифметическим квадратным корнем из числа 36;
г) число 0,7 не является арифметическим квадратным корнем из 4,9.
64. Имеет ли смысл выражение:
![]() д)
д) ![]()
![]()
65. Найдите значение корня:
|
14 2— 25 |
![]()
![]() 6)
6) ![]() в)
в)![]() д) 3666.
д) 3666.
49
66. Найдите значение выражения:
а) при![]()
![]()
|
в) при х 0,49; 1; 36; 121. 67. Найдите значение выражения: |
|
|
|
68. Решите уравнение: |
в) 0,25-16-7 |
1
49 |
![]()
|
|
г) 56 |
е) 46-3=0; |
з) 10х-12 =13. |
69. Запишите без знака модуля:
![]() а) 1151 = 6) l-161 =
а) 1151 = 6) l-161 = ![]()
в) l01 —![]()
г) la2 1—
![]()
д) la3 , где![]()
е) la3 , где![]()
4. Уравнение
х![]()
Это уравнение имеет решения при а 0 .
Если а = 0, х имеет корень х .
![]()
![]()
![]() Если
а то х имеет два корня х —Г
Если
а то х имеет два корня х —Г![]()
![]() Примеры:
1) х2 = 25;
Примеры:
1) х2 = 25; 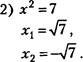
70.
![]() Имеет ли корни уравнение:
Имеет ли корни уравнение:
а) х2 = 64 ;
71. Решите уравнение:
![]()
![]()
![]() 2
=121 ; д) 60+у2 =64 ; и) 0,3х 2 ;
2
=121 ; д) 60+у2 =64 ; и) 0,3х 2 ;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1
![]()
![]() з) —4х2
з) —4х2
25'
72.
73. ![]()
ж)
2
74. Вычислите:
![]() в)
(247)2
в)
(247)2 ![]() ,
,
![]()
х
75.
Найдите значение выражения —![]()
х
![]() а) при х —-9; -4; 2; 10; 125;
а) при х —-9; -4; 2; 10; 125;
б) при х > 0;
в) при х < 0.
5. Функция у = Сх и её ирафик
Знать форму графика (смотри рис. З)
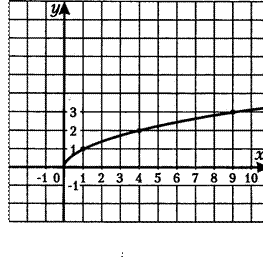
Свойства функции у = •.G
1. Если х — 0, то у — 0. Начало координат принадлежит
графику функции. ![]()
2.
З. Большему значению ар1умента
соответствует большее значение функции; график функции с увеличением х идет
вверх. 5 > 4, следовательно, > ![]()
4. График функции у —47 српюиетррнен графику функции у = х при х 20 относительно прямой у = х .
76. По графику функции у = Сх (рис. З) найдите:
а) значение Сх при х = 3,5; 6; 8,5;
б) значение х при у = 1,5; 2,5; 2,7.
77. Принадлежат ли графику функции у = точки:
а)
А(36; 6); ![]() в) C(-81; 9);
в) C(-81; 9); ![]()
78. Пересекает ли график функции у = 6 прямая:
1 ![]() в) у: 100; -100 ?
в) у: 100; -100 ?
2
79. Укажите область определения функции и постройте схематшески график:
![]()
![]()
80. Сравните:
![]() 1
1 ![]() д)Ф7 и З
д)Ф7 и З![]() З
З ![]()
![]()
81. Расположите в порядке:
а)
возрастания числа: ; ...Дб ; ..јб3 ; ; фбЗ![]()
![]()
б) убывания
числа: ![]() 5; Гб
5; Гб![]()
82. Найдите значение выражения:
![]()
![]()
83. Решите уравнение:
а) х2 =5; ![]()
![]()
в) 2х2 1
![]() г) 36= 2 . 8З
г) 36= 2 . 8З
Тест 2. Арифметический квадратный корень Вариант 1
1. Арифметическим квадратным корнем из числа а называется
1) число квадрат которого равен а;
2) неотрицательное число, квадрат которого равен а;
З) корни уравнения х = а ;
4) отрицательный корень уравнения х![]()
2. Значение выражения (—53) равно
2)- 10; 4) 75.
З. Решите
уравнение 6х![]()
2)![]()
4.
Расположите в порядке убывания числа: 0,4;![]()
![]()
![]()
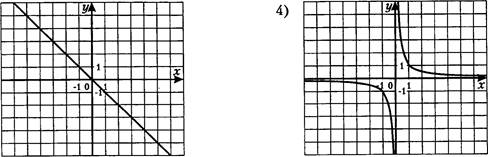
5. График функции у = изображен на рисунке
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
-1 0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)
|
252-242 |
|
25 |
6. Найдите значение выражения
Ответ:![]()
7. Укажите
все целые числа, расположенные между числами 4 и ![]()
Ответ:![]()
Вариант 2
1. Квадратным корнем из числа а называется
1) неотрицательное число, квадрат которого равен а;
2) число, квадрат которого равен а;
З) положительный корень уравнения х = а ;
4) отрицательное число, квадрат которого равен а.
2. Значение выражения (—43) равно
З. Решите уравнение 11х![]()
11
2)-1; ![]()
4. Расположите
в порядке возрастания числа: 0,7 ; .јб7![]()
![]()
2)
0,7; 467; С, ![]()
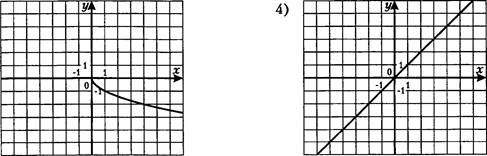
5. График функции у = —6 изображен на рисунке
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)
|
|
|
6. Найдите значение выражения
Ответ:
![]()
7. Укажрите все целые числа, расположенные между числами ИЗ
Ответ:
![]()
6. Свойства арифметического квадратного корня
Квадратный корень из произведения и дроби
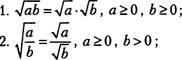
з. га.љ=г;;;
а
4.![]()
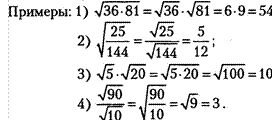
84. Найдите значение выражения:
а) 2,25-144 ;![]()
|
|
|
е)
108-48 ; з) ![]()
85. Вычислите значение выражения:
|
1 2 |
 а)
202 -162 , в)
а)
202 -162 , в)![]() ж)
ж)
6)
122 +52 , г) ![]() з)
з)
Квадратный корень из степею«

![]()
32
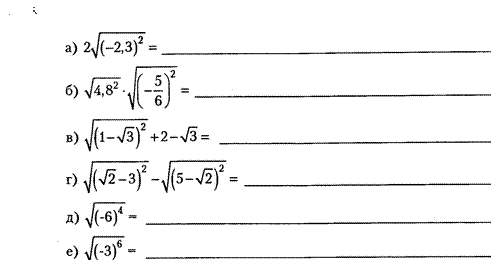
87. Упростите выражение:
![]()
при х 20; б)
-50+60-![]()
при У<О; ![]() в)
0,4467-
в)
0,4467- ![]()
при а ;
![]()
при х 21.
7. Вынесение множителя за знак корня, Внесение множителя под знак корня
![]() на 645 называют вынесением множителя за
знак корня.
на 645 называют вынесением множителя за
знак корня.
![]() называют внесением множителя под знак
корня.
называют внесением множителя под знак
корня.
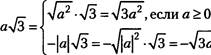 —•Љ7, если а < О
—•Љ7, если а < О
88. Вынесите множитель за знак корня:
![]() б) 4566;
б) 4566;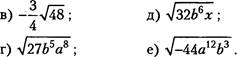
89. Внесите множитель под знак корня:
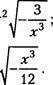
![]()
![]() 4
4 ![]() ж) 2а
ж) 2а ![]() и) —5х а
и) —5х а
б)
-100 ; г) -46 ; е) --хФТх з) —4х ![]() к) 6х2
к) 6х2
4
90. Сравните:
![]() б) и 70,
б) и 70, ![]() г) -т и 10
г) -т и 10
8. Преобразование выражений, содержащих квадратные корни
91. Упростите выражение:
![]()
![]() б)
С3(2С3+Г2) ;
б)
С3(2С3+Г2) ; ![]()
92. Сократите дробь:
|
|
|
94. Решите уравнение, предварительно упростив его правую часть:
![]()
б) х2 9+43- 9-4$)2,
2 ![]()
Тест З. Квадратњке корни
![]() Вариант
Вариант ![]()
|
а —25 2. Сократите дробь |
2) |
4) (2-46)2 ? |
|
га+5 |
|
|
1 1) а—5; 3) га-5, |
1 4) |
|
а—5 З. Найдите наименьшее среди чисел. |
Га-5 |
|
1) 54 ; 4.
Выполните действие (44— 1) 12; 2) 54 ; 5. При а выражение а1 %8 можно заменить выражением. |
4) 64.
|
|
1) —а%4 ; 2) a5b4 ; З) —а%б , 6. Внесите множитель под знак корня в выражении х |
|
![]() 1. Значение какого из следующих выражений является
иррациональным числом
1. Значение какого из следующих выражений является
иррациональным числом
![]()
|
7. Решите уравнение х |
|
|
|
|
2) -.дсз; |
3) -646; |
К заданиям 8—10 запишите решение.
8. Выполните действия![]()
![]()
![]()
10. Найдите значение дроби х2 +3ху + у2
при х=2+ЈД и ![]()
![]()
Вариант 2
1. Значение какого из следующих выражений является рациональным числом
![]() 150
150
2. Сократите
дробь![]()
![]()
|
З. Найдите наибольшее среди чисел. 3) 347 4. выполните действия (6-ф)2 -аз.т |
|
|
1) 25; 2) 13; 5. При а выражение a12b4 можно заменить выражением: |
4)- 1. |
|
1 |
10 2 |
![]() З)
—а%2 ,
З)
—а%2 , ![]()
|
5 |
6. Внесите
множитель под знак корня в выражении х2 ![]()
![]()
7. Решите уравнение 2х2 =16.
![]()
К заданиям 8—10 запишите решение.
![]() 1
1
8. Выполните действия
![]()
![]()
х2 —3xy+Y2
10. Найдите значение дроби при ![]() х—у—10
х—у—10
![]()
ПИ. КВАДРАТНЫЕ УРАВНЕНИЯ
1. Неполные квадратные уравнения
Определение. Квадратным уравнением называется уравнение вида ах +bx+c=O , где х переменная, а, Ь и с — некоторые числа, причем а О .
Числа а, Ь, с — коэффициенты квадратного уравнения.
Число а называют первым коэффициентом (старшим), число Ь — вторым коэффициентом (средним), число с — свободным членом.
Примеры: 1) 2х2 —3х+5=0, а = 2, Ь = —3, с = 5;
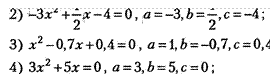 1
1
5) —4х2 +6 = 0, а = —4, = 0, с = 6 ;
7) х2 +4х а = 1, Ь с=О.
Если коэффициент а = 1 , то уравнение имеет вид х +bx + с = 0 , такое уравнение называют приведенным квадратным уравнением.
Уравнения З, 7 — приведенные квадратные уравнения.
Если в квадратном уравнении хотя бы один из коэффициентов Ь или с равен то такое уравнение называют неполным квадратным уравнением.
Так уравнения 4—7 — неполные квадратные уравнения.
Неполные квадратные уравнения имеют вид: 1) ах2 +bx = 0, с![]()
2) ах2 +с = 0,![]()
З) ах2 = 0, Ь = с = 0.
Перед решением неполных квадратных уравнений внимательно прочитайте пункт «Неполные квадратные уравнения».
95. Какие из уравнений:
|
а) 5,2х 2 -3х+2=0 ; |
в) 3х—х2 —1=0; |
д) 5х 2 |
|
6) 48х3 — 2 +9=0; |
г) —4х2 —13 = 0; |
е) 3х+4 = 0. |
являются квадратными?
96. Выпишите коэффициенты квадратного уравнения:
2)
х2 —4х—3=0; ![]()
3)
-х2 -7х+1=0;
![]() 4) +9х=о;
4) +9х=о; ![]()
6) 8х2![]()
Какие из данных уравнений являются приведенными квадратными уравнениями и какие неполными квадратными уравнениями?
97. Найдите корни уравнения:
|
а) 25х2 -16=0; |
в) 0,1х2
—10=0 |
16 |
|
98. Решите уравнение: |
г) 5х2 +125=0 |
|
|
а) 5х2 —8х ; |
в) 10х2 +4х=0; |
д) 7у2 |
|
б) —5х2 +7х=0; 99. Решите уравнение: |
г) 4а2 —5а |
е) 3У+4у |
![]()
![]() а) 5х2 —4х+9 = 3х2 +2х+9
; ж)
(5х+2) 2
а) 5х2 —4х+9 = 3х2 +2х+9
; ж)
(5х+2) 2![]()
б)
(х+3)(х—З)=9;![]() з) (—х+5) 2
з) (—х+5) 2![]()
![]() и)
х2 +6х+9=0.
и)
х2 +6х+9=0.
2. Решение квадратного уравнения по формулам
Решение уравнения ах +bx+c где а * 0, b 0, с .
1) 4х2 —4х+1=0 ,
(2х-1)2 ,
1
Ответ: х =![]()
2
![]() ¯ 4х + 4 ¯ 4 ¯ 21
¯ 4х + 4 ¯ 4 ¯ 21 ![]() (х-2)2 =25,
(х-2)2 =25,
х—2=5 или х—2=—5, х = 7 или х=—З Ответ: — З; 7.
Решение уравнения (1) ах +bx+c=O в общем виде.
Умножим обе части уравнения на 4а , т.к. а 0.
4а х +4abx+4ac=0.
(2ах)2 +2ах .b+b2 —b2 +4ас = 0 .
(2) (2ax+b)2 —4ас .
Далее все зависит от числа b2 —4ас .
1) b2 —4ас=0 , тогда (2ax+b)2 = 0, 2ax+b=O , х = ——.
Уравнение имеет один корень.
2) b2 —4ас >0 , то уравнение (2), а значит и (1) имеет два корня.
З) b2 —4ас < 0 , то уравнение (2) не имеет корней, а значит и уравнение (1).
Обозначим число b2 —4ас = D . ![]()
Уравнение (2) принимает вид:
(2ax+b)2 ![]() b2 —4ас .
b2 —4ас .
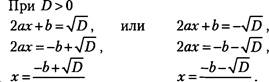
2а
Объединим записи этих корней
![]() D = b2 —4ас
называют дискриминантом.
D = b2 —4ас
называют дискриминантом.
Пример. 3х2-7х+4=0
![]()
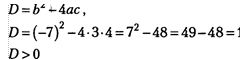
Уравнение имеет два корня
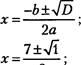
6
6 6
![]()
4
Ответ: 1; —![]()
З
100. Вычислите дискриминант квадратного уравнения и укажите число его корней:
а) 5х2 +8х—4 ;
101. Решите уравнение:
а)
х2 +5х—24![]()
б) 3у2 7![]()
в) (х+1)2 =7х-зх2.
г) х2 —(2х—3)(1—х)=З;
![]()
7
г) —х2 —5х+6 = О;
![]() 2у+5
2у+5
е) 10 2
ж) lx2 +4х—8 —4![]()
з) х2 —3lxl-4=0;
![]()
![]()
д) 5х+х2 —6=0;
е) х2 -12х+36=0.
х
2 —5х—6— = 0;
х
2 ![]()
![]()
Вторая формула корней квадратного уравнения ах +bx+c = 0 , Ь — четное число
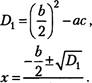
а
Пример. 5х2 +14х—3![]()
Ь = 14 — четное число, — ![]() 2 2
2 2
![]()
5
-7-8 —7+8
![]()
5 5
1
х
![]()
1
Ответ: — З; — ![]() 5
5
102. Решите уравнение:
в) х2 +18х+65 = О;
г) (х2 ![]() —14х+16) ;
—14х+16) ;
д) 1х2 —x—141 =ix2 —5х+61 ;
![]()
![]()
к) (Х+2)2 —2(х+2)—15=0;
![]()
![]()
н) (-2х2![]()
![]() 1—х
1—х
п)
16 4 2
103. При каких значения а уравнение:
а) (а—1)х2 +2(2а +1)х+4а +3 имеет один корень,
б) (а+6)х2 +2ar+1 имеет единственное решение?
З. Решение задач с помощью квадратных уравненй
Перед решением задач внимательно прочитайте пункт учебника с таким названием.
104. Одно из натуральных чисел на 4 меньше другого. Найдите эти числа, если их произведение равно 525.
105. Длина прямоугольника на 7 см больше ширины, а его площадь равна 60 см2. Найдите стороны прямоугольника.
106. Найдите длины сторон прямоугольника, периметр которого равен 32 см, а площадь равна 55 см2.
107. От
квадратного листа фанеры отрезали прямоугольную полосу шириной 2 дм, в
результате площадь оставшейся части листа составила 24 дм . Найдите
первоначальную площадь листа. ![]()
4. Теорема Виета х +px+q=0
D
= р2 —4q ![]()
При D >0 уравнение имеет два корня, которые обладают свойством 2 Это
![]()
теорема Виета.
![]()
Для уравнения ах +bx+c = О теорема Виета
имеет вид а при D![]()
![]()
а
Пример. Найдите сумму и произведение корней уравнения 5х —12х+ 7 = 0 . Решение. D = 144 —140 = 4, 4 , уравнение имеет два корня х1 и х2.
12 7
По теореме Виета х1 +х2 =![]()
5 5
108. Найдите сумму и произведение корней уравнения:
а) 2х2 —х—З![]()
б) —х+2+Х2![]()
в) х2 -7х+10=0.
109. Найдите подбором корни уравнения:
|
6) Ё -11х-12=0; в) х2 +4х—12=0; |
д) х2
е) В +13х+12=0. |
110. Не вычисляя корней х1 и х2 уравнения х —6х+8 = О , найдите:
![]() 6) +хтХ1 ;
6) +хтХ1 ; ![]() 4 4
4 4 ![]()
111. При каких значениях а уравнение
( 2а —6а+8)х
+ а ![]()
имеет более двух корней?
112. Один
корень квадратного уравнения х —6x+c=0 равен: а) 3+3 ; б) 2+3 ![]() Найдите другой
корень и значение с.
Найдите другой
корень и значение с.
113. Составьте квадратное уравнение, если его корни равны:
б)![]()
114. Решите уравнение:
а) (х—3)2![]()
![]() (х— 1)2 2х—1
(х— 1)2 2х—1
12 з 4
Тест 4. Квадратные
Вариант 1
1.
7
2. Сколько корней имеет уравнение 7х2-25х-12=0?
З. Решите уравнение 6х2 +31х +5 = 0 .
1 1
![]()
4. Если х1 =—6, х2 =З — корни уравнения х +px+q = О , то
1 5. Составьте квадратное уравнение, зная, что числа и З его корни. з
![]() 1) х2 —8х—1=0 ; 2)
3х2 -8х-3=0; 3) 3х2 +8х-3=0;
1) х2 —8х—1=0 ; 2)
3х2 -8х-3=0; 3) 3х2 +8х-3=0;
6.
Определите значения у, при которых верно равенство у2 _ 9у-2 ![]() 7
7
2 2 2
![]()
![]() 7 7
7 7
Для заданий 7—10 запишите решение
7. ![]() Решите
уравнение: х +6 = 5х .
Решите
уравнение: х +6 = 5х .
![]()
7
1
![]()
6
4) р = ![]() •
• ![]() —18
—18
4) х2![]()
2
![]()
7
![]()
8.
Решите уравнение: х 2 — ![]() 2
2
![]()
![]()
9. Решите уравнение: х2 +47—12 = 0
![]()
![]()
10.Разность корней уравнения х +12x+q = О равна 4. Найдите корни уравнения и q.
![]()
![]()
Вариант 2
1. Из чисел —4; 0; 2 корнями уравнения 3х +10х—8 являются
22
2. Сколько корней имеет уравнение 3х2-25х+12=07
З. Решите уравнение 3х +14х—5=0.
![]() З)
З)![]()
ЗЗ
4. Если х1 =—8;х2 = 2 — корни уравнения х +px+q = 0 , то
![]()
2
5. Составьте
квадратное уравнение, зная, что числа 4 и![]() его корни.
его корни.
1) Ё -10х-8=0; 2) 3х2
-10х-8=0;![]() +10х—8=0 •
+10х—8=0 •![]()
у2 +10у 2У+5
6.
Определите значения у, при которых верно равенство ![]()
10 2
2
![]()
![]()
4) p=6;q=16.
4) 3х2 +10х+8=0![]()
Для заданий 7—10 запишите решение
7.
Решите уравнение: х +8 = 6х . ![]()
![]()
![]()
8.
Решите уравнение: х 2 —![]()
![]()
![]()
9. Решите уравнение: х 2 —47-6=0.
![]()
![]()
10. Разность корней уравнения х +18x+q=O равна 6. Найдите корни и q.
![]()
![]()
5. Дробные рациональные
Решение дробных рациональных уравнений
При решении дробных рациональных уравнений поступают следующим образом:
1) находят общий знаменатель дробей, входящих в уравнение;
2) умножают обе части уравнения на общий знаменатель; З) решают получившееся целое уравнение;
4) исключают из его корней те, которые обращают в нуль общий знаменатель.
![]() 2х 144 Пример.
2х 144 Пример.
х +6 х2 —36
Общий знаменатель (х+ 6) (х —6) .
Умножив обе части уравнения на общий знаменатель, получим целое уравнение.
![]()
![]()
![]()
![]()
![]() 2х(х—6) — 144 = х2 —36 , отсюда
2х(х—6) — 144 = х2 —36 , отсюда
![]() 2х2
2х2
![]() Если
х то (6—6)(6+6) = 0
Если
х то (6—6)(6+6) = 0
Если
Корнем исходного уравнения является число 18.
Ответ: 18
115. Найдите корни уравнения:
![]()
![]()
![]()
![]()
![]()
![]() х 7х+35 2х-3 1 4х-6 а)в) д)
х-5 х2 -25 хх +2х
х 7х+35 2х-3 1 4х-6 а)в) д)
х-5 х2 -25 хх +2х
![]()
![]() Хх
+2х—8 7 х 2 32
Хх
+2х—8 7 х 2 32
![]()
![]()
![]()
![]() 6)г) е)
6)г) е)
116. Решите уравнение:
х _9
![]()
![]()
![]()
![]()
![]()
![]() а)—0;
в)д)ж) х-з х2+9
а)—0;
в)д)ж) х-з х2+9
2
![]()
![]()
![]()
![]() х 3х
6)г)е)з) х -4 lxl-3
х 3х
6)г)е)з) х -4 lxl-3
х 117. При каких значениях
переменной равны дроби — и ![]()
118. Решите уравнение:
![]()
![]() х—З
х—З
а)= —2 , введя новую переменную х +4х+9 х—З
х
—х+З х![]()
6)![]() =5, обозначив х —х+1
за t, т.е. х —x+1=t; х —Х+1 х
=5, обозначив х —х+1
за t, т.е. х —x+1=t; х —Х+1 х![]()
5 8
в) ![]() = 2 , обозначив х(х+4) = х2 +4х
= t.
= 2 , обозначив х(х+4) = х2 +4х
= t.
6. Решение задач с помощью рациональных уравнений
Пример. Скорость течения реки равно 2 км. Теплоход затратил на 50 км пути по течению реки и 8 км против течения З часа. Какова собственная скорость теплохода?
Решение.
Пусть собственная скорость теплохода х км/ч. Далее оформим решение задачи в виде таблицы
|
Движение |
Ско сть в км ч |
П ть в км |
В емя в часах |
|
По течению |
|
50 |
50 |
|
Против течения |
|
8 |
8 |
Из условия задачи следует, что на весь путь теплоход затратил З часа, следовательно,
50 8
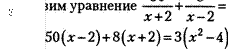 (х+2)(х—2);
(х+2)(х—2);
50х-100+8х+16=3х2-12;
![]()
29+25 29-25
4
Если х = 18, то
4
![]()
![]() —, то (х+2)(х—2)
—, то (х+2)(х—2)
4
По смыслу задачи х > 2 , поэтому х=— не подходит
Ответ: 18 км/ч.
![]() Решите задачу.
Решите задачу.
а) Две машинистки, работая совместно, могут перепечатать рукопись за 8 часов. Сколько времени потребовалось бы каждой машинистке на выполнение этой работы, если одной для этого потребуется на 12 часов меньше, чем другой?
б) Расстояние из А в В длиной 60 км мотоциклист проехал по проселочной дороге, а обратно возвращался по шоссе, сократив путь на 5 км и увеличив скорость на 10 км/ч. С какой скоростью ехал мотоциклист из А в В, если известно, что на путь по проселочной дороге он затратил на 6 минут больше, чем на путь по шоссе.
120. Решите задачу.
Расстояние между пристанями А и В равно 36 км. Из А в В по течению реки отправился плот, а через З часа вслед за ним отправился катер, который, прибыв в пункт В, тотчас повернул обратно и возвратился в А. К этому времени плот прошел 24 км. Найдите скорость катера в неподвижной воде, если скорость течения реки равна З км/ч.
Тест 5. Дробные рациональные
Вариант 1
2
1. Корнями уравнения являются числа:
![]()
2. Равносильными являются уравнения:
2
х 36
![]() и х2 =36;
и х2 =36;
5![]()
2)![]() и х+1=6;
и х+1=6;
4) ![]()
З. Значение функции у = равно 0 при х, равном:
![]()
4. Решите уравнение:
2
У 4
а)![]()
б) ![]()
5. Решите задачу.
Велосипедист проехал 5 км по лесной дороге и 7 км по шоссе, затратив на весь путь 1 час. По шоссе он ехал со скоростью на 4 км/ч большей, чем по лесу. С какой скоростью велосипедист ехал по лесной дороге?
Вариант 2
1. Корнями уравнения являются числа: х-з х-з
![]()
2. Равносильными являются уравнения:
х2 —9
1) ![]() =0 их +3х=0; х +3х
=0 их +3х=0; х +3х
2) ![]() и В +25=0;
и В +25=0;
2
![]() и х-7=0.
и х-7=0.
З. Значение функции у = равно О при х, равном:
![]()
4. Решите уравнение:
2
У 36
а)![]()
б) ![]()
5. Решите задачу.
Пешеход прошел по шоссе З км, а по проселочной дороге 6 км, затратив на весь путь 2 часа. С какой скоростью шел пешеход по проселочной дороге, если известно, что по шоссе он шел со скоростью на 2 км/ч больше, чем по проселку?
IV. НЕРАВЕНСТВА
1. Числовые неравенства
Определение. Число а больше числа Ь, если разность а—Ь — положительное число; число а меньше числа Ь, если разность а—Ь — отрицательное число; число а равно числу Ь, если разность а—Ь равна 0.
На координатной прялкой большее число изображается точкой, лежащей правее, а меньшее — точкой, лежащей левее.
Пример. Сравните а и Ь, если
![]() , следовательно, а ;
, следовательно, а ;
, следовательно, а > Ь ;
в) b+a = 1+ b2 , следовательно, а = —b+ 1+b2 , вьщелим а —Ь = —2b+ 1+b2 = b2 — % + 1 = .
(b—1)2
20, следовательно, 0 , значит а Ь![]()
121. Сравните а и Ь, если:
![]() г)
a=b+2,7; ж) a+1=2b и b>1;
г)
a=b+2,7; ж) a+1=2b и b>1;
д) а—З=Ь—с,с<З; 3) а +2=Ь+С И с 22 ;
![]() и) b+a=2+b2 .
и) b+a=2+b2 .
|
122. Сравните числа:
|
в) 323-325 и 3242 , |
|
13 12 6) |
г) 742 -272 и 732 -262 . |
123. Сравните выражения:
а) (а—1)(а+2) и (а+4)(а—З);
б) а2 +25 и 10а ;
в) 8+5 и 2b+3;
г) а4 +1 и 2alal;
д) (а—2)2 и 4(1—а).
124. Докажите, что при любом значении переменной верно неравенство:
а) (х—4)2 >Х(х—8);
![]()
Ь 1
![]()
г) а4 +1628а+2а З.
2. Свойства числовых неравенств
Теорема 1.
Если а , то b<a и если а , то Ба.
Суть этой теоремы в том, что если в верном неравенстве поменять местами левую и правую части, то надо поменять и знак неравенства, тогда оно будет верным.
Примеры: 1) 5, тогда 5> 2;
2) —3<—1, тогда —1>—3;
![]()
Теорема 2.
Если a<b и b<C, то а<с. Если а >Ь и b>c , то а >с.
Примеры: 1) 2<7 и 7<10 , то 2<10 ;
![]()
Теорема З.
Если а и с — любое число, то а+с < b+C
Если а и с — любое число, то а+с > ь +с .
Суть теоремы: если к обеим частям верного неравенства прибавить одно и то же число, то получится верное числовое неравенство.
Следствие.
Если a<b+c, то а—с<Ь и если a+c>b, то а >Ь—с. Слагаемые в неравенстве можно переносить из одной части в другую, изменив при этом знак у слагаемого.
Примеры: 1) 2<7,то 2—3<7—3, т.е. —1<4 ;
2)
8>—З,то 8+5>—З+5,т.е. 13>2. ![]()
Теорема 4.
Если а и
с ![]() , то ас < Ьс . Если а >Ь и с
, то ас < Ьс . Если а >Ь и с ![]() , то ас >Ьс .
, то ас >Ьс .
Если а и
![]() , то ас .
, то ас .
Если а и ![]() , то ас < Ьс .
, то ас < Ьс .
Словами эту теорему можно сформулировать так: если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство; если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
Примеры: 1) 3<10 и —>0,то —<5;
2) 6>4 и —2<0,то —12<—8 или —3<—2.
Следствие.
![]() 1
1
Если а и Ь положительные числа и а < Ь , то —>— или а
> Ь , то —<—![]()
![]() 1
1
Примеры: 1) 2<3 то —>— ![]() 2 3 '
2 3 '
|
|
|
З) —>—, то —<2.
125. Известно, что а < Ь . Сравните:
а) а +1,2 и Ь +1,2 ;
б) а—4,З и Ь—4,З;
в) —3а и -3b;
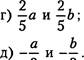
з З
126. Какими числами (положительными или отрицательными) являются числа а и Ь, если верны неравенства:
а) а—5>Ь—5 и Ь>З;
6) а-1О>Ь-1О и «-13;
1
в) 9a>9b и
b>— ![]() 3 '
3 '
2 г) —3a>—3b и b<——.
5
127. Известно, что а > Ь . Используя свойства неравенств, запишите верное неравенство, которое получится, если:
а) к обеим частям этого неравенства прибавить число 10;
б) из обеих частей этого неравенства вычесть число 8;
З
в) обе части этого неравенства умножить на число ![]()
2
г) обе части этого неравенства
разделить на — ![]() 3 '
3 '
д) обе части этого неравенства умножить на —1 .
128. Каков знак числа а, если известно, что:
а) ба < За ; б) 9а > 4а ; в) —4а < 4а ; г) —14а < —2а ?
129. Известно, что c . Объясните, на основании каких свойств можно утверждать, что верно неравенство:
г)
—0,01с +0,7 > —0,01d + О, 7 ; ![]()
З З
130. На координатной прямой отмечены числа.
![]()
Расположите в порядке возрастания числа —
а
![]()
З. Сложение и умножение числовых неравенств
Теорема 5.
Если a<b и ![]() , то
a+c<b+d .
, то
a+c<b+d .
![]()
Если а >Ь
и ![]() a+c>b+d .
a+c>b+d .
Без символики теорему можно сформулировать так: неравенства одного знака можно почленно складывать, получим неравенство того же знака.
Примеры: 1) 2<7 и —3<—1, тогда 2—3<7—1 , т.е. —1<6;
![]()
|
Теорема 6. Если а
<Ь и Если а >Ь и |
и а, Ь, с, d—
положительные числа, то ас < bd |
Теорему можно сформулировать так: неравенства одного знака с положительными членами можно почленно перемножать, получим верное неравенство с тем же знаком.
Примеры:
|
|
10>2 |
|
|
23>3 |
Следствие. Неравенства с положительными левой и правой частями можно возводить в любую натуральную степень, получим верное неравенство того же знака, т.е. если а > Ь или а < Ь а и Ь — положительные числа, то ап > или ап < . Это следствие можно сформулировать иначе.
Если
а , то а273+1![]() 2n+i
2n+i
Если а , то а273+1![]() 27i+i , где а и Ь —
любые.
27i+i , где а и Ь —
любые.
Если а <Ь и а ![]()
Если а >Ь и а БО, то а >b 2k![]()
Примеры: 1) 2<3 , то 23 < 33 , т.е. 8< 27
44
11 1
2) —>—, то , Т.е. — ![]() 216 81
216 81
3) ![]() -3<2, то
(-3)3 , т.е.-27<8 но (—3)4 < 24 неверно
-3<2, то
(-3)3 , т.е.-27<8 но (—3)4 < 24 неверно
131. Сложите почленно неравенства:
а) 14>—6 и 10>7;
![]()
132. Перемножьте почленно неравенства:
![]() 1
1
б) 6<12 и
—<—![]()
Двойные неравенства
Неравенства вида:
1) Ь<а<с; 2) Ь Да'с•,
![]()
называются двойными.
Чаще используются неравенства ( 1 ) и (2).
Неравенства (1) и (З) называются строгими, а (2) и (4) нестрогими. Все рассмотренные свойства верны и для двойных неравенств.
133. Пусть
5 <а<б и ![]() 15 . Оцените:
15 . Оцените:
а
а)
a+b; ![]() в) ab;
в) ab; ![]()
134. Известно,
что 1,4 ![]() < 1,5 и 2,2 < 2,3. Оцените:
< 1,5 и 2,2 < 2,3. Оцените:
а) 45+45; б) .ЈЗ-Ф ; г) Ф6; д) -3“.
135. Известны границы длин основания Ь и боковой стороны а равнобедренного треугольника, выраженные в сантиметрах 2,6 ' а 2,8 и 4,1' Ь 4,3 . Оцените, в каких границах периметр этого треугольника.
136. Если 3< х <9 и 4 < у < 12 , то оцените значение выражения— и выберите верный ответ:
У
137. Известно, что ![]() 5' уд 7.
Оцените значение выражения х—2у и укажите верный
5' уд 7.
Оцените значение выражения х—2у и укажите верный
ответ:
2)
-10'х— 2у —8 ; ![]()
138. Используя неравенство о среднем арифметическом и среднем геометрическом ab , 2 где а 0, Ь 20 , докажите:
а) (аз ![]() ;
;
б) ![]()
139. Используя неравенство а 2 , где а > 0 , докажите неравенство
а
1 1
![]() 22.
22.
Ilorpeumocfb H TOYHOCTb![]()
IIycTb x a.
![]() Ix—al — a6c0J1i0THæq
norpe111HocTb.
Ix—al — a6c0J1i0THæq
norpe111HocTb.
A6COJIK)THOVf norpe11.1HocTbK) 11PH6JIHXeHHOro 31--1aqeHHA Ha3b1BaiOT MOAYJ1b pa3HOCTH TOYHOro H 11PH6JIHXeHHOro 3HaqeHHA.
MHCJIO
h Ha3b1BaK)T TOYHOCTbkO 11PH6JIH%CeHHOro 3HaqeHHfl, ecJIH X —al h![]()
IIH111yr: x = a c ![]() h HJIH x =a±h .
h HJIH x =a±h .
HepaBeHcTB0 Ix—al S h MOXHO aaMeHHTb HepaBeHCTBOM —h x —a S h HJIH a—h x a +h .
OTHOCHTeJ1bHOii norpe111HOCTbi0 11PH6JIH%CeHHOro 3HayeHHA Haa3b1BaeTCA OTH0111eHne
|
|
|
|
|
a |
a6COJHOTHOi norpe11.1HocTH K
MOAYJIÆO 11PH6JIHXeHHOro 3HaqeHHH, T.e.![]()
a
![]() OueHKa
OTHOCHTeJ1bHOii norpe111HOCTH — a
OueHKa
OTHOCHTeJ1bHOii norpe111HOCTH — a
FlpHMep:
17,26![]()
140. Hai%ÅHTe a6COJ1iOTHYK) norpe111HOCTb 11PH6JIH%CeHHOro 3HayeHHA, 110J1yyeHHoro B pe3YJ1bTaTe 0KpyrJ1eHnn:
a) qmcna 7,85 no emHHH11;
6) MHCJ1a 234 no neCATKOB;
B) tmc..na 0,653 no neCATb1X;
r) MHCJ1a 0,298 AO COTb1X.
2
141. IIPH Bb1110JIHeHHH BblYHCJ1eHHi mp06b 3a.MeHHJIH neCATHYHOi ap06bi0 0,67. KaK0Ba 3 a6c0JH0THax norpe111HOCTb 3Toro 11PH6JIH)KeHHH?
142. B KaKHX rpaHHIIax 3aK.moqeHO MHCJIO y, eCJIH:
![]()
![]()
143.
OKpyrmrre MHCJIO
3,625 no meCATb1X. ![]() OTHocwreJ1bHYO norpe111HOCTb 11PM6JIHxeHHA, nonyyeHHoro OKpyrJ1eHHH.
OTHocwreJ1bHYO norpe111HOCTb 11PM6JIHxeHHA, nonyyeHHoro OKpyrJ1eHHH.
144. Ha Kop06Ke KOH4)eT YKæaH0, HTO OHa AOJIXHa xpaHHTcn Ter„mepaType 170 ± 20 C . YAOBJ1eTBOPAeT JIH 3TOMY YCJIOBVffO Tewreparypa B03myxa, paBHan:
a) ITC, 6) 220C; B) 16,5 00, r) 13,5 0C.
Пересечение и объединение множеств
Определение 1.
Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.
Определение 2.
Объединением двух множеств называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств.
Пример. Пусть А — множество натуральных делителей числа 24, а В — множество делителей числа 20. Выпишем эти множества А ={1; 2; З; 4; 6; 8; 12; 24} , В = {1; 2; 4; 5; 10; 20} .
С = А оВ — пересечение множеств А и В
![]()
D = А ив — объединение множеств А и В. D 2; З; 4; 5; 6; 8; 10; 12; 20; 24} .
145. Пусть Х — множество четных натуральных чисел, не превосходящж 16, а У — множество двузначных натуральных чисел, не превосходящих 16. Задайте множества Х и У перечислением элементов и найдите их пересечение и объединение.
146. Задайте путем перечисления элементов множество А двузначных чисел, являющихся квадратами натуральных чисел, и множество В двузначных чисел, кратных 15. Найдите пересечение и объединение этих множеств.
147. Найдите пересечение и объединение:
а) множества цифр, используемых в записи чисел 12543 и 5361;
б) множеств букв, используемых в записи слов «алгебра» и «биология»;
в) множество составных чисел, не превосходящих 30, и множества двузначных чисел, кратных 10.
148. На рисунке изображены углы
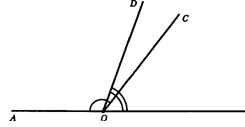
Какая фигура является:
а) пересечением углов АОС и DOB;
б) объединением углов АОС и DOB?
149. С помощью кругов Эйлера проиллюстрируйте соотношение между множеством чисел, кратных 5, и множеством чисел, кратных 15.
Какое множество изображает общая часть этих кругов?
4. I-IHCJIOBb1e 11POMe*YTKH
BHHMaTeJ1bHO 11POMVfTaTb IIYHKT.
YMeTb MHTaTb HepaBeHcTBa H 3a11HCb1BaTb MHCJIOBb1MH 11POMeXYTKaMVf H 31--1aTb reoMeTPHqecKYK) HHTepnpeTaumo.
|
HepaBeHcTB0 |
MHCJIOBOMf 11POMeXYTOK |
reoMeTpvrqecKan HHTe 11 eTa11H% |
|
|
(— 5; 4) — HHTePBaJ1 0T — 5 mo 4 |
|
|
|
|
|
|
|
— 110JIYHHTePBaJ1 0T — 5 mo 4, BK.noqan — 5 |
—UUUZUUUUUUUZ.—» |
|
-5<xs4 |
— 110JIYHHTepBaJ1 0T — 5 mo 4, BKJIK)qan 4 |
|
|
|
(8 — OTKPb1Tb1Mf MHCJIOBOÜ JIYY 0T 8 no +00 |
|
|
x 28 |
— MHCJIOBOMI 0T 8 mo +00 |
|
|
|
( —00; 9) — OTKPb1Tb1Mf MHCJIOBOM 0T — 9 |
|
|
|
(—00; 9] — MHCJIOBOMI 0T — 00 no 9 |
|
MHOXeCTBO
meiCTBHTeJ1bHb1X MHCeJ1 H306paxaeTcq Bceä KOOPÅHHaTHOif ![]() Ero HUb1BaoT KOOPÅHHaTHOi
11PHMOi H 0603HaqaK)T TaK: (-00; + 00).
Ero HUb1BaoT KOOPÅHHaTHOi
11PHMOi H 0603HaqaK)T TaK: (-00; + 00).
150. P1306pa3HTe Ha KOOPÅHHaTHOMf IIPAMOMI npoMexyroK H Ha.30BHTe ero:
![]() B) [0; 10];
B) [0; 10];
151. Vf306pa3MTe Ha KOOPÅHHaTHOü IIPHMOMI MHOXeCTBO MHCeJ1, YAOBneTBOPAk01UHX HepaBeHcTBy:
![]()
![]()
![]() m)
—2,5sx S 12 ; 3) 9<xS15;
m)
—2,5sx S 12 ; 3) 9<xS15;
e)
—3 < x < 2,5 ; ![]()
152. FIPHHaÅJ1eXHT JIH
a) HHTePBaJIY (— 6; 7,5) MHCJIO: — 7; — 6; — 5; — 3,9; 0; 5; 6) 0Tpe3KY [—10; 0] MHCJIO: — 12; — 10; — 8; — 1,5; 0; 1?
153. Kmcvre uejlble MHCJ1a 11PHHau.nexaT npoMexyTKy:
![]()
154. Mc110J1b3YA KoopÅHHaTHYK) IIPAMYK), HaVUIHTe nepeceqeHHe H 06%eÅHHeHme IIPOMOKYTKOB:
|
a) (2; 9) H (5; 12); 6) [-10; 10] H 12] ; B) [—7;6) H (—4; 8]; |
r) (5; +00) H (8; +00);
e)
(7; +00) H —oo;l |
5. Решение неравенств с одной переменной
Определение.
Решением неравенства с одной переменной называется значение переменной (число), которое обращает его в верное числовое неравенство.
Пример. Рассмотрим неравенство 6х—3 > 10 .
Число 5 является решением данного неравенства, так как ![]() 10
верно, а число 2 не является решением, так как 6 • 2—3 > 10 неверно.
10
верно, а число 2 не является решением, так как 6 • 2—3 > 10 неверно.
Решить неравенство — значит найти все его решения или доказать, что решений нет.
Неравенства, имеющие одни и те же решения, называются равносильными. Неравенства, не имеющие решений, считают таюке равносильными.
При решении неравенств используют свойства, которые сохраняют равносильность:
1) Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.
2) Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство; если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Например, неравенство 15+3х>0 равносильно неравенству 3х > —15 , а неравенство 3х > —15 разделив обе его части на З, можно заменить равносильным х > —5 .
Решением неравенства х >—5 является любое число, больше — 5, а значит и неравенство 15 + 3х > 0 имеет такое же множество решений.
Пример решения неравенства.
Рассмотрим неравенство 18х < 15х—21.
Перенесем 15х с противоположным знаком в левую часть неравенства: 18х — 15х < —21 .
Приведем подобные члены: 3х < —21.
Разделим обе части неравенства на З: х < —7 .
Множество решений неравенства х состоит из всех чисел, меньших — 7.
Это множество представляет собой открытый числовой луч (![]()
Ответ: —7)
При решении неравенств мы заменяем заданное неравенство равносильным ему неравенством вида ах > Ь или ах <b , где а и Ь — некоторые числа.
Неравенства ах >b или ах <Ь называют линейными неравенствами с одной переменной.
Решите неравенства:
![]()
Ответ: (1,5; +00)
![]()
Ответ: (— 2; +00)
З) < 6 ; при любом значении х данное неравенство равносильно 0 <6 верно.
Значит решением 0 • х < 6 является любое число. Ответ: (— о.; +00)
4) можно заменить числовым 0>5, которое неверно, значит у неравенства нет решений или его множество решений — пустое множество. Ответ: решений нет.
![]() 155. Является ли решением неравенства бу
> З(у —2) +18 значение у, равное:
155. Является ли решением неравенства бу
> З(у —2) +18 значение у, равное:
в) 1,5;
156. Укажите
три каких-либо решения неравенства 4х < 3х — 7![]()
157. Решите неравенство и изобразите множество его решений на координатной прямой:
а)
2x<19•, ![]()
б) 6х2—4 ; е) -18х <-27 ;
![]() в)
—15х ;
в)
—15х ;
|
158. Решите неравенство: |
|
|
|
|
|
|
и) |
2 н) 2х-9 |
|
б) (6-3)х4; |
е) зЛ(5-2х) > 10(5-2х) ; |
|
2 о) 2х+5 |
|
|
ж) |
л) |
(х-5)2 п) |
![]()
![]()
![]()
![]() г) —х > —8,5;
г) —х > —8,5;
46-10 3х-124х + 16
![]() Х2 +36(Х+2)2 г)
Х2 +36(Х+2)2 г)![]() м)
м)![]() р)
р)
гз-Ф2х-52х+9
159. При каки значениях переменной имеет смысл выражение:
|
12х—1 З |
|
|
|
|
25 |
![]() в) д)
в) д)
|
9—5а |
|
15 |
![]() г) е)
-(15-зх) ?
г) е)
-(15-зх) ? ![]()
160. Найдите область определения функции:
10
|
1 2(х-5)- (6Х+15) з |
![]() а)
у: ;
а)
у: ; ![]()
161. Решите неравенство относительно r.
б)
3•(2а+х)<1—ах; д) ![]()
2 З 6
в)
(а—1)х+а<З+2х; ![]()
162. Найдите множество значений а, при которых уравнение:
а) х +2х+4а+З=О не имеет корней;
б) (а+6)х2 +2х+1 имеет два корня;
в) (а—1)х2 —2ах+а+2=0 не имеет корней.
6. Решение систем неравенств с одной переменной
Внимательно прочитать пункт учебника с таким заголовком.
Определение.
Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.
Решить систему — значит найти все её решения или доказать, что решений нет.
Чтобы решить систему неравенств, надо решить каждое неравенство, входящее в систему и найти пересечение множеств решений этих неравенств.
4х-26<0,
163. Какие из чисел — З; 0; 4; 5; 6 являются решениями системы неравенств
2х—1<5 ? 164. Является ли число 5 решением системы неравенств:
5х > —8х + 9, 2х-6>-14, а) б) 2х-5>0; 3х-10<8 ?
165. Решите систему неравенств:
а) ![]() б)
б) ![]()
166. Решите двойное неравенство:
8—х 4—х 1
16 З 2
167. Решите неравенство:
![]()
![]() в)
в) ![]() ж) х—2
ж) х—2
|
б) |
3х—1 г) 22 ; |
х) 2х-3 до; |
з) (х—5) |
168. Найдите область определения функции:
![]()
169. При каких значениях у имеет смысл выражение:
|
2 |
![]() В)
В) ![]()
170. При каких значениях а выполняется равенство:
![]() =
За-10 ; 6) l5-4al = 5-4а ; в) 118-9al -1; г)
=
За-10 ; 6) l5-4al = 5-4а ; в) 118-9al -1; г)
а)
18—9а
Тест 6. Неравенства
Вариант 1
1. На координатной прямой отмечены числа х; З; у.
![]()
Укажите верное неравенство
|
1) З-у>О •, 2) х-3>0; 2. Если а то |
3) x-Y<O • |
4) 3—х <0. |
|
1) a+6<b+6; З. Сравните значения выражений 4b2 +1 и 4b . |
З) a+6=b+6; |
4) а +6'Ь+6. |
|
1) 4b2 +1>4b ; 2) 4b2 +1 ; |
3) 4b2 +1<4b; |
4) 4b2 +124b. |
4. Укажите число, удовлетворяющее неравенству 3х —8 > 9 .
5. Решением неравенства 5х—20 < 1 является множество
![]() 3) 4,2)
3) 4,2) ![]()
4—х < 6,
6. Укажите число, удовлетворяющее системе неравенств
4х-3<0 :
7. Пересечением числовых промежутков (—8; 3] и [—5; 6) является промежуток
![]()
8. Каждому неравенству сопоставьте соответствующий числовой промежуток.
![]()
![]() 4)
4)![]()
Запишите в таблицу под каждой буквой соответствующий номер
|
|
|
в |
|
|
|
|
9. Решите неравенство —(4х+1) 5(х+4) .
10.
Решите систему неравенств 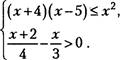
5—х i 1. Решите двойное неравенство —2 < <З .
6
12. Докажите
неравенство (а— 2) (а —6) < (а —3) (а —5) . ![]()
13.
Укажите наибольшее целое решение неравенства (4 —Л)х > 40 —807![]()
Вариант 2
1. На координатной прямой отмечены числа 5; х; у.
![]()
Укюките верное неравенство
|
2. Если а >Ь, то |
3) x-Y<O |
|
|
З) а—12<Ь—12 и a+4<b+4; |
|
2) а-12<Ь-12 и а+4>Ь+4; |
4) а—12>Ь—12 и a+4<b+4. |
![]() З.
Сравните значения выражений 6b и 9b2 +1
З.
Сравните значения выражений 6b и 9b2 +1
|
1) 6b>9b2 +1; 2) 6b=9b2 +1; 3) 6b29b 2 +1 ; 4. Укажите число, удовлетворяющее неравенству 5х +8 > —9 3) - 3,4; 5. Решением неравенства 6х+ 20 > 2 является множество |
4) 6b'9b 2 +1. |
![]()
6. Укажите число, удовлетворяющее системе неравенств
5х-4>17.
|
1) 4,2; |
4) 14; |
7. Объединением числовых промежутков [—9; З) и [—6; 7) является промежуток
![]()
8. Каждому неравенству сопоставьте соответствующий числовой промежуток
![]()
![]() 2)
[5; +00).
2)
[5; +00).![]()
Запишите в таблицу под каждой буквой соответствующий номер
|
|
|
в |
|
|
|
|
9. Решите неравенство 1,4х—5 —2(2,6—О,5х) .
10.
Решите систему неравенств 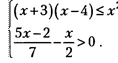
11.
Решите двойное неравенство —3![]()
12
12. ![]() Докажите
неравенство (а —4) > (а —5) (а —2) .
Докажите
неравенство (а —4) > (а —5) (а —2) .
13.
Укажите наименьшее целое решение неравенства ![]() — 5) х <
48 — 10“5
— 5) х <
48 — 10“5
V. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ. ЭЛЕМЕНТЫ СТАТИСТИКИ
1. Определение степени с целым отрицателышм показателем
Определение. а ![]() , где а и п — целое отрицательное число.
, где а и п — целое отрицательное число.
![]()
Примеры: 1) 6-2 62 - 36'
![]()
(-2) 16
3) 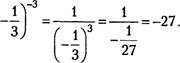
![]() Замечание: 1) 01 = 02 —
Замечание: 1) 01 = 02 —
не существует
, где п — натуральное
![]() —
и а взаимно обратные.
—
и а взаимно обратные.
-3
![]() 27
27
32
243
171. Вычислите:
![]()
![]() а) 5-2
а) 5-2![]() г) (—1) 10 ,
г) (—1) 10 ,
![]() д)
д)
-7
в)
(—1)![]() е) и) 0,01 -3
е) и) 0,01 -3![]()
172. Найдите значение выражения:
![]() а) -10-5 ,
а) -10-5 ,![]()
б) —0,25-3 ,![]()
173. Вычислите:
О![]()
![]() а)
8-12-1 , в) 6-2 —3-2
а)
8-12-1 , в) 6-2 —3-2 ![]() д)
0,5-3 + Ж) (1,4)
д)
0,5-3 + Ж) (1,4)![]()
б)
—8-8-2 ; г) 1,40 ![]() е) 10. - 3)
360 +0,
е) 10. - 3)
360 +0,![]()
174. Представьте в виде дроби выражение:
![]()
![]() б)
ху-2 + ху-1 , г) (х-1 —2у-1
б)
ху-2 + ху-1 , г) (х-1 —2у-1 ![]() +2у-1 е) (a+b)-
+2у-1 е) (a+b)- ![]()
2. Свойства степени с целым показателем
Для любых а 0, Ь * 0 и любых целых т и п ![]() т+п
. 2) ат : ап т—п .
т+п
. 2) ат : ап т—п .
З) (ат у![]()
4) (ab)n![]()
5)![]()
![]() Примеры: 1) а -16
•а14 _ -16+14
Примеры: 1) а -16
•а14 _ -16+14
![]() —5+3)
—5+3)
![]() 4
4 ![]()
3)
(2a2b-3 ) = 24 (а2 •(b-3)4![]()
175. Найдите значение выражения:
|
а) 4-4 .46 , |
г) 211 . 213 |
ж) (2-3 |
|
6) 2-5 .23 ; |
|
-2 з) (53 ) • 54; |
|
в) 109 .10-5 10 176. Вычислите: |
|
и) 3-5 |
![]()
![]() -17
16. 9-4 .275 ,
-17
16. 9-4 .275 ,
г)
б)![]() д) 125-5 :
д) 125-5 : ![]()
1254
в) 8-3![]()
177. Упростите выражение:
-2
![]() а)
1,5х зу12 • 6х4 у-10
а)
1,5х зу12 • 6х4 у-10 ![]() г)
г)
-1
5 2-4
б) х-4 у 5 •30ху д)
6
—З -1
![]()
![]() з
з
-3 -43х в) (0,25х у2 х-
У
З. Стандартный вид числа
Определение. Стандартным видом числа называют его запись в виде а• 10п , где 1 'а < 10 и п — целое число.
Число п называется порядком числа.
Примеры: 1) 125000 = 1,25-105 ,
![]()
|
а) 1,3-108 , в) 2,7-10-4 |
|
|
|
|
6) 4,8-103 , г) 7,6-10-1 , 179. Запишите в стандартном виде число: |
|
е)
8,75-10 5 |
|
|
а) 63 000 ; в) 75 |
; |
д) 0,00345 ; |
ж) 47-104 ; |
|
6) 3195 000 ; г) 52,44 ; |
|
е) 0,0000047 ; |
з) 0,83-107 . |
178. ![]() Укажите порядок
числа, представленного в стандартном виде:
Укажите порядок
числа, представленного в стандартном виде:
180. Выразите:
а) т в граммах;
б) 2,8• 10-4 км в сантиметрах;
![]() в) кг в тоннах;
в) кг в тоннах;
г) см в метрах;
д) 3,65• 109 см в километрах;
е) ![]() гв тоннах.
гв тоннах.
181. Выполните умножение и результат представьте в стандартном виде:
а) (4,25-10 ) (2,4-10 )![]()
![]()
в) (5,63-10- ) (4,2-10-2).
66
Тест 7. Степень с це.лым показателем. Стандартный вид числа
Вариант 1
1. Вычислите 4- ![]()
1) 2)![]()
2. Запишитев виде степени с основанием а.
![]() а
а
3) а-14 ![]()
З. Вычислите![]()
![]() 25 25
25 25
1)![]() 2)
2)![]()
4. Возведите в степень
1)
у-13 ![]() 3) у40 ;
3) у40 ;
5. Запишите в стандартном виде число 40300.
1)
40,3-103 ; 2) 4,03-104 ; ![]() 4)
0,403-105
4)
0,403-105
6. Для каждого числа укажите его порядок, вписав в таблицу под каждой буквой соот ветствующий номер ответа.
А) 8300 Б) 0,083 В) 8,3 Г) 0,0083

7. Вычислите
![]()
35 18
8. Вычислите.
![]()
9. Найдите значение выражения 2,3 • 10-5 (6-104 Результат представьте в стандартном виде.
Вариант 2
1. Вычислите 2- ![]()
2.
Запишите ![]() в виде степени с основанием у.
в виде степени с основанием у.
2) у-15![]()
З.
Вычислите —2— ![]()
![]() 125 125
125 125
1) 2)![]()
125
|
4. Возведите в степень |
а |
|
|
-11. |
|
и |
![]()
![]() 2) а,
2) а,
5. Запишите в стандартном виде число 2402.
1)
240,2-101 ; 2) 24,02-102 ; 3)
2,402-103 ; 4) 0,2402-10-4![]()
6. Для каждого числа укажите его порядок, вписав в таблицу под каждой буквой соот ветствующий номер ответа.
А) 950 Б) 0,95 В) 9,5 г 0,0095

7. Вычислите
![]()
7 16 .3 13
8.
Вычислите![]()
21-15
9. Найдите значение выражеения 8,7 • 10-7 (3-104) Результат представьте в стандартном виде.
4. Элементы статистики
Из 7 класса надо знать статистические характеристики: среднее арифметическое, размах, мода, медиана.
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда (ряд, где числа записаны в порядке возрастания) чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине. Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Пример. Рассмотрим числовой ряд 30; 32; 36; 40; 41; 42; 49; 50.
30-4-32-4-36 + 40 + 41 + 42 + 49 50
1) = 40 — среднее арифметическое данного ряда
8
2) 50—30 = 20 — размах ряда
40+41
3)
![]() = 40,5 — медиана ряда
= 40,5 — медиана ряда
2
4) моды нет
182. Можно ли считать выборку представительной, если при изучении времени, которое затрачивают на выполнение уроков восьмиклассники:
а) опрашивали только мальчиков;
б) опрос проводили только по средам;
в) опрашивали только учащихся гимназий?
183. Ряд данных о количестве акций одинаковой стоимости, приобретенных сотрудниками фирмы представлен в виде таблицы частот.
|
Число акций |
Частота |
|
2 |
20 |
|
5 |
10 |
|
10 |
7 |
|
20 |
2 |
|
25 |
4 |
|
100 |
2 |
Найдите для этого ряда данных среднее арифметическое, размах и моду.
184. В фермерском хозяйстве площади, отведенные под посевы зерновых, распределены следующим образом:
пшеница — 60 %; овес — 17 %; просо — 13 %; гречиха — 10 96.
Постройте круговую диаграмму, иллюстрирующую распределение площадей, отведенных под зерновые в данном фермерском хозяйстве.
5. Функции у
=х-![]() х- и их свойства
х- и их свойства
1 1 -2 1
![]()
х х2
1 1 1) Свойства функции у = х-![]()
х
Область определения: х — любое число, кроме 0.
Область значений: у — любое число, кроме О. Если х>О, то у ; если х , то у <0.
Графиком является гипербола, расположенная в первой и третьей четвертях координатной
плоскости.
Противоположным значениям аргумента соответствуют противоположные значения функции.
При х функция убывает и при х функция убывает.
-2 1 2)
Свойства функции у = х![]()
х
Область определения функции: х — любое число, кроме 0.
Область значений функции: у >0 , т.е. УЕ (0; +00) ![]()
График расположен выше оси х в первой и второй координатных четвертях.
Любым противоположным значениям аргумента соответствуют одно и то же значение функции.
При х у возрастает и при х ![]() у возрастает.
у возрастает.
185. Постройте график функции:
х, если х 0, х- , еслих>О;
х , если —1' х ' 1, х- , еслих<—1,х>1.
1 -2
186.
Известно, что точки А а; и B(0,64;b) принадлежат графику
функции у = х ![]() 256
256
![]() Найдите а и Ь.
Найдите а и Ь.
6. Дисперсия и среднее квадратичное отњлонение
Определение. Дисперсией ряда чисел называется среднее арифметическое квадратов отклонений от среднего арифметического этого ряда.
Пример. Рассмотрим числовой ряд 7; 4; 5; 10; 6; 5; 10; 15.
7+4+5+10 +6+5+10+15
Среднее арифметическое этого ряда равно
8
Для каждого члена ряда найдем его отличие (его отклонение) от среднего арифмети-
ческого:
![]() 5-7,75=-2,75; 10-7,75 =
2,25 ;
5-7,75=-2,75; 10-7,75 =
2,25 ;
6-7,75=-1,75; 5-7,75=-2,75; 10-7,75 = 2,25 ; 15-7,75=7,25. Найдем сумму отклонений:
![]()
Сумиа отклонений для любого ряда равна О и не может характеризовать разброс данных ряда.
Составим ряд квадратов отклонений и вычислим среднее арифметическое этого ряда.
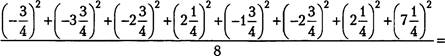
9 225 121 81 49 121 81 841 -16 16 16 16 16 16 16 16
|
9+225+121+81+49+121+81+841 |
1528 |
120 |
|
16-8 |
128 |
128 |
= 11,9375 — это и есть дисперсия.
187. Для ряда чисел 4; 6; 9; 10; 7; 2 найдите:
а) среднее арифметическое;
б) отклонение каждого члена ряда от среднего арифметического;
в) дисперсию ряда.
Тест 8. Итоговый тест
Вариант 1
1. Решите уравнение 2х2-5х+2=0.
![]()
2. Какое из уравнений имеет иррациональные корни?
З. Сократите дробь ![]()
|
|
|
3) |
|
|
64 — а 4. Представьте в виде дроби |
16—2а |
|
|
|
а —2а+1 |
а—1 |
|
|
![]()
![]() 1)
1) ![]() 3 2) ' 3)
3 2) ' 3)
![]()
2(а—1) 2(а—1) 2(а-1)
220
5.
Вычислите ![]()
8,8
2) 25;
6. Внесите множитель под знак корня -!фТа .
![]()
7. На каком чертеже, изображен график функции у = ?
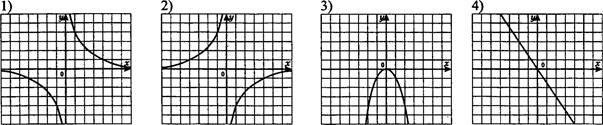
8. Изготовитель гарантирует, что каждый кусок обоев имеет длину м. Длина первого куска 9,7 м, длина второго куска 10,11 м. Какой из кусков имеет гарантируемую длину?
1 ) только первый; 2) только второй; З) имеют оба; 4) не имеет ни один.
9.
![]() Решите систему неравенств6х+4 > 2(5—4х),
Решите систему неравенств6х+4 > 2(5—4х),
3х-5<5Х+5.
![]()
![]() +00
+00 ![]() 3)
3)![]()
7
10. Решите уравнение
![]() З) 4)
корней нет.
З) 4)
корней нет.
![]() а
а
11. Упростите выражение а—х
12. Постройте график функции у =
Ё -10х+25
13. Решите задачу.
Две машинистки должны были
напечатать по 60 страниц каждая. Одна машинистка за 1 час печатает на 2
страницы меньше, поэтому закончила работу на 1 час позже. Сколько страниц в час
печатала первая машинистка?
Вариант 2
1. Решите уравнение 2х -х-з=о.
|
1) 2. Какое из уравнений имеет рациональные корни? |
3) |
|
1) Х2 +2х+2=0; +2х-6=0; х2 —8х+16 З. Сократить дробь 8-2х |
|
|
4—х 1) а2 —16 8-2а 4. Представьте в виде дроби |
3) |
![]()
![]()
![]() (а+4)(а—З)(а+4)(З—а)
(а+4)(а—З)(а+4)(З—а)
![]()
![]() 1)
1) ![]() 2) 3)
2) 3)
|
5. Вычислите |
|
|
|
|
3) 16; |
4) 32. |
6. Внесите
множитель под знак корня —5..,тТ![]()
![]()
7. На
каком чертеже изображен графин функции у =![]()
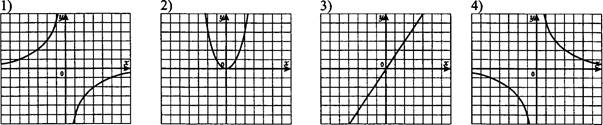
8. Изготовитель
гарантирует, что каждый моток провода имеет длину ![]() м. Длина первого 4,92
м, а второго 5,01 м. Какой моток имеет гарантируемую длину?
м. Длина первого 4,92
м, а второго 5,01 м. Какой моток имеет гарантируемую длину?
1 ) только первый; 2) только второй; З) имеют оба; 4) не имеет ни один.
5х-18дз(Х+2),
9. Решите систему неравенств
4х-8>3х-12.
![]() 2) 12); 3)
12] ;
2) 12); 3)
12] ; ![]()
х +4х 4х+25
10. Решите уравнение х—5 х-5
![]() 4)
корней нет.
4)
корней нет.
11. Упростите
выражение ![]()
Х +4х-4- 4
12. Постройте график функции у =
![]()
13. Решите задачу.
Рабочий и ученик должны изготовить по 40 деталей.
Рабочий изготавливал за 1 час на З детали больше, чем ученик, поэтому весь
заказ он выполнил на З часа раньше. Сколько деталей выпускал за 1 час ученик?
Ответы
Повторение изученного в 7 классе
![]() 1.
1. ![]()
2. ![]()
з. 2)
4.
1) 5ab+4c2 , 2)
2х2 +8у ; ![]() 4) —12х 2 +1.
4) —12х 2 +1.
5. а) 4х3 —13х2 —З; б) —2y2 + Зу— 15 .
6.
![]() 2) 0,5.
2) 0,5.
7.
а) —ба%2 +
2а%З —![]() 6) 15х3 +20х 2 -6х-8.
6) 15х3 +20х 2 -6х-8.
8.
![]() 1) 9х2 +12х+4 ; 8) 4ab ;
1) 9х2 +12х+4 ; 8) 4ab ;
2)
36у4 -84у2 +49; 9) —168 + 26ab+
2b2 ; ![]()
З) —а2 —ab+4b2 , 10) -18х2 -54 ;
16
4) х2 -10х+25 ; 11) т -25;
9. 1)
2)
![]() З) —3Х+9).
З) —3Х+9).
4)
б) (x—a—b)(x—a+b); г) (p—a+b)(p+a—b); 10. ![]()
|
а |
б |
в |
г |
|
2 |
з |
5 |
|
Проверочная работа Вариант 1 ![]() 1.
1.
![]() 2. 2
2. 2
з. 1) —ба4 -4- 2аз —2а2. З)
8х2у—9ху2![]()
2) -5х5 -2у5—6; 4) 3ab3 +a2b2 —5 .
4. а) а2 + а +2 ; В) Х2 +5,5х+6 ;
6)
16; г) 12тз —13n2![]()
5. а) баз —24а2 —12а ; в) 1,5у3 -3,75у2 +9у ;
б)
—12х4 +12х3 +8х2![]() г) —3а%З +3a%+3ab3
.
г) —3а%З +3a%+3ab3
.
6. а) аз +ab—a2b2 —b3 , в) а4 —4а +4а2.
б)
81—х4![]() г) Заз +12а2 +12а
.
г) Заз +12а2 +12а
.
![]() 7.
7.![]()
4) 8ab ;
![]() 2 4
2 4
8. ![]() 2)
-3,5 3)
2)
-3,5 3) ![]()
19
Вариант 2
|
а |
б |
в |
|
|
З |
5 |
4 |
|
1.
2. З.
З. 1) —5а4 —5аз +11а2. З) —7ху2 +3х2у ;
2)
11у5 -6х3 -З; 4) —a3
b3 —2a2 b2 —5a 2b—4 ![]()
4. а) х2 —х—5; в) -2х2 -2,5х+4 ;
б) —5а2 —ба+7 ; г) 9a2b2
+8 +4b2![]()
5. а) 10аз +358 -20а ; в) -2,5у3 +3,75у 2 -шу •
6) 20х4 -12х3
-8х2 , г) 10х3 уз +5х3 у—5ху![]()
6. а) 9у2 —х4 в) х4 —6х3 +9х2.
6) 25-у4 ; г) 5х3 +40х2 +80х .
7.
![]() 5) (2х—а—Ь)(2х+а+Ь).
5) (2х—а—Ь)(2х+а+Ь).
2) (х+1)2 (х—1) ; 4) 120;
8.
![]() 4) 6; 12.
4) 6; 12.
I. Рациональные дроби
12. ![]()
13. а) х — любое число, кроме — 8; в) х — любое число, кроме 0; д) а — любое число.
б) b — любое число, к оме — 4 и 4;
|
|
-9 |
|
|
-2 |
- 1 |
4 |
12 |
1 2 |
1 |
|
|
36 |
4 |
6 |
12 |
18 |
36 |
|
|
-72 |
108 |
не существует |
14. а)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
32 |
9 |
|
з43 |
|
З |
32 |
|
6)
2 5 1 7 9 24 40 28 54 36
15.
а)![]() б)
б)![]()
16.
1) Да при с![]() 2) нет; З) Да при —5; а
.
2) нет; З) Да при —5; а
.
17.
а) Да при а 4; б) Да при а![]()
1) Верные при всех а, кроме: а) 4; б) ±5. 2) Тождественным преобразованием.
З) Замены его на тождественно равное при всех допустимых значениях переменных.
4) Умножение и деление дроби на одно и тоже выражение, отличное от 0. 5) да.
2а а а+5 a—b
18.
![]() в)
в) ![]() ж) 2
ж) 2
З 5 ' а—5 а2 —ab+b
х 1
![]() г)
9х; е)з) a+b.
г)
9х; е)з) a+b.
Зу
![]() 19.
19. ![]() б) х
Зу
б) х
Зу![]()
20. у=х—2
при х * 2; 4)![]()
б) 2—а;
![]() 22. б)
4(с—
22. б)
4(с—![]()
![]() 25(Зх-у)
25(Зх-у)
![]()
![]() 23. а)б)
23. а)б)
5П (25-1)
![]() За + х
За + х
24.
![]() а)б)
а)б)
25.
![]() а)б)
а)б)
26. а) —х—а;
![]()
![]()
![]()
![]()
![]() б)г) а—З
б)г) а—З
![]()
![]()
![]() 27. а)б) 2
27. а)б) 2
![]() а—б (х —6) 2а Ь
а—б (х —6) 2а Ь
![]()
![]()
![]() 28.б)
28.б)
2а2 ба
29.
|
|
б) |
г) |
а2 +5а—1 |
|
31. |
2а2 —b2 а) ' a(a+b) |
в) |
|
12х
![]() 6х— 2 б) ' г)
6х— 2 б) ' г)
х(х—2)
|
х(х—2)(х+2) |
х(х—2)2 |
32. а) ' б)
![]() 33. а) б)
33. а) б)
16—х
13х
![]() в)
в)
5х
![]() 90х
90х
б) 3х2 ; г)
24а(а+2) 2ху(х+Зу)
35. а) ' б)'
|
|
9mn |
32xy3 |
2(з-х) |
|
|
|
3x |
г) |
е) 2(а+2). |
|
|
38. |
|
a+4b |
|
2(4b+a) |
|
39. |
a—b |
|
|
|
36.
![]()
![]()
![]()
![]()
![]()
![]() а)
а) ![]() б)
б) ![]() 16
16 ![]() 4ab
4ab
37.
а)![]() в)
в)![]()
![]() 2(х+3)
2(х+3) ![]() б) г) тп(т+Зп) '
б) г) тп(т+Зп) '
х —2x+4
40. а)![]()
![]() a—b
a—b
![]() а)
а)![]()
42. а)
да,являются при а # О, а # ;![]() 2; -3,3 .
2; -3,3 .
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
16 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
45. к
= ху![]()
![]()
![]() 10
10
46.
—1#1.
Проходит. Не проходит. Не проходит.
|
|
|
|
|
|
|
|
„-2x+3 |
У = 2x |
47.
![]()
![]()
![]() 32
32
32 ![]()
2•2х х
Тест 1. Рационалыне дроби
Вариант ![]() Вариант
2
Вариант
2
1. 2 1. 2 2. 2
6. 6.
х(х—2)
х¯У 7. 2(a—b) 7.
У
4х(х—2). 7 (х—4)2 49
![]() 8.
8.
х—5 12
26
![]() х—1
х—1
2 6
Смещенная влево на 1 гипербола у =![]() Смещенная вправо на 1
гипербола у = —
Смещенная вправо на 1
гипербола у = —![]()
х х К 1 1 1 К 1 К 1
10.![]() 10.
10.![]()
|
|
а) Неверно; б) Неверно; |
в) Верно. |
|
50. |
0,7- 10 - зо
—5_ 19 38 |
|
![]() II.
Квадратные корни
II.
Квадратные корни
|
1 ¯2 5 |
|
|
51. |
14 ¯ — ¯ , |
|
1 1 10 |
10 6 6 9 9 |
|
52. а) — 0,666... |
е) 12,27 |
|
б) — 0,41666... — 12 |
ж) —18=-18,000... |
|
в) |
з) —0,3125000... |
|
7 |
16 |
|
-2,111... - ; |
|
|
|
40 |
|
д) —— = —0,2666...= —0, 2(6) ; |
к) |
|
15 |
11 |
|
53. |
, т.к. —1— 40 |
|
|
|
|
8 |
1 з 14 |
![]() 1 2
1 2
![]()
![]() 17 18 1 17 1
17 18 1 17 1
![]() следовательно, 144 144
следовательно, 144 144
56. а) Верно; б) нет; в) верно; г) верно.
57.
Рациональные: 0; —; 0,57; ![]() 516 .
516 .
58.
![]() 1,4286;
1,4286; ![]()
8
4
![]() г) 3,142 ; е) —4(16) <
—4—
г) 3,142 ; е) —4(16) <
—4— ![]() 25
25
2 59. ![]() 6) АВ=2-
6) АВ=2-![]()
60. — 4,75...,- -4,64...; 3(6); 5,62.
61.![]()
б) Аналогично a+b 5,11.
в) a+b z 5,117.
62.
а) ![]() 58,8 ;
58,8 ; ![]() -45,2; a-b=
-45,2; a-b= ![]() = 13 6
= 13 6![]()
б) Аналогично а —Ь 13,56 .
63. а) = 7 верно, так как 7 > 0 и 72 = 49 ;
б) верно, так как 0,5>0 и = 0,25 ;
в) •Ј5б = —6 неверно, так как —6 < 0 ;
г) = неверно, так как = 0,49 # 4,9 ;
![]() Имеет смысл в пунктах
б; в; г; д. Не имеет смысла в пунктах а, е.
Имеет смысл в пунктах
б; в; г; д. Не имеет смысла в пунктах а, е.
2 8
![]() 65. в)
65. в)
![]() д) 60.
д) 60.
66.
б) Вычисляем аналогично: 8; 11.
|
в |
х |
0,04 |
,49 |
1 |
36 |
121 |
|
|
|
— 0,16 |
- 0,21 |
|
|
110 |
Если х =0,04 , то![]()
67. а) 13,9; 6) 75;
68.
![]() д) 144; ж) решений нет;
д) 144; ж) решений нет;
1 9
6) 0,09; г)![]()
2516
69. а) 15;
6) 16; 2.
70.
имеет: а,![]() не имеет: г
не имеет: г![]()
![]()
71.
![]()
![]()
![]()
![]() а) ±11 ; и) ±10;
а) ±11 ; и) ±10;
ж) ±10;
з) решений нет;
72. а) а 20;б) х 20;
|
73. |
|
в) -45; |
д) 1,25; |
|
|
|
г) 2,1; |
е) 27; |
|
|
|
|
|
10 |
125 |
|
|
|
|
|
|
|
|
х |
3,5 |
|
8,5 |
|
|
|
|
|
![]()
![]() 74. а) 1,64; 6)
38; в) 76;
74. а) 1,64; 6)
38; в) 76;
75. а)
76. а)0
|
77. |
а) Принадлежит; |
б) не принадлежит; |
в) не принадлежит; |
г) принадлежит. |
|
78. |
а) Пересекает; |
б) пересекает; |
в) пересекает; |
г) не пересекает. |
79.
![]() д)
д) ![]()
б) х — любое число г) х 22
80. 3 2 .
81. 82.
83. 6) 25;
Тест 2. Арифметический квадратный корењ
Вариант 1
![]()
Вариант 2

|
и. |
а) 18; |
в) 0,022; |
д) 720; |
ж) 6,5; |
|
|
б) |
35 |
е) 72; |
|
|
85. |
а) 12; 6) 13; |
|
д) 12; |
|
86. а) 4,6;
е) 27.
87. а) —2x ; в) —1,6а;
Г)![]() (х—1)[2] —х
+3
(х—1)[2] —х
+3 ![]() = 2 .
= 2 .
88.
![]() д) 41b3 1•..G
д) 41b3 1•..G![]()
![]() 89.
89.
90.
91.
92.
2 4
93. в) 845+20; д) 60-2; ж) ![]() а—4 х(б-гу)
а—4 х(б-гу)
б) г)
З
2
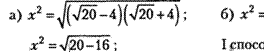 ( 9+43- 9-4$)
( 9+43- 9-4$)

95. ![]()
96.
97. а) ±0,8 ;
![]()
98. а) 0; 1,6;
6) о; 1,4; 99.![]()
в) решений нет;
100. а) два корня;
б) корней нет;
101. 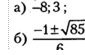
в) 0,25; 1;
2
7 102.![]()
|
|
а |
|
|
|
1 |
6 |
- 10 |
7 |
|
2 |
1 |
-4 |
-3 |
|
|
|
|
|
|
4 |
1 |
9 |
|
|
5 |
5 |
|
|
|
6 |
8 |
|
|
III. Квадратные уравнения
Приведенные в пунктах 2 и 4. ![]() Неполные в пунктах 4;
5; 6.
Неполные в пунктах 4;
5; 6.
|
г) решений нет; |
е) решений нет. |
|
в) — 0,4; 0; |
1 7 |
|
г) о; 1,25; д) решений нет; е) 0,5; 2,5; |
е) - 0,75; О. ж) решений нет;
|
|
в) два корня; |
д) два корня; |
|
г) два корня; |
е) один корень. |
е) -15; 15;
![]()
![]()
п) Ф;4Ф .
8
|
3' д) уравнение распадается на два: х — х— 14 = х —5х+6 или х —х—14=-( 2-5х+6) . |
![]() в) -13; -5;
в) -13; -5;![]()
Ответ: -1; 4; 5.
![]()
ж)![]()
103. а) При а = —0,8; а = 1 ;
![]() 21; 25. 105. 5; 12. 106. 5;
11.
21; 25. 105. 5; 12. 106. 5;
11.
107. 36.
1 з 108.![]()
2 2 109.![]()
з)![]()
44
и) корней
нет;![]()
б) при а = —6;
а = —2; а = З![]()
б) корней нет; в) Х1 +Х2 = 7 ; Х1 •Х2 = 10 ![]()
![]() 12;- 1.
12;- 1.
110.
![]() Сумма корней х1 +х2 = 6 ; произведение х1 •х2 = 8 .
Сумма корней х1 +х2 = 6 ; произведение х1 •х2 = 8 .
г) 272.
111.
Более двух корней возможно при а —ба+8=0 ; at = 2 ; а2 = 4![]()
Если а = 2 , то уравнение принимает вид 0 а
х![]() ; 0=0 верно при любом значении х.
; 0=0 верно при любом значении х.
З
Если а = 4 , то уравнение принимает
вид 0 х2 +12x+10-12-16=0; 12x-18=0 ; х =![]()
2
Ответ: при а = 2 .
![]() 112.
112. ![]()
из.В) Х2 +11x+30=0 ;
|
б) х2 |
2 8 х |
или 3x2 —2x—8=0; |
г) х2 —11x+30=0 . |
з з
![]()
![]() б) Уравнение можно заменить системой х =
1 или х = 2;
б) Уравнение можно заменить системой х =
1 или х = 2;
Ответ: 2.
4
Тест 4. квадратные уравнения
Вариант 1
|
|
2 |
з |
4 |
5 |
6 |
|
7 |
8 |
9 |
|
|
4 |
2 |
2 |
З |
2 |
2 |
|
|
4 |
|
|
|
|
|
|
|
|
Вариант 2 |
|
|
|
||
|
1 |
2 |
з |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
|
з |
з |
2 |
З |
2 |
1 |
|
|
5 |
|
|
![]() 115.
115. ![]()
116. ![]()
б) решений нет; г) решений нет;
|
117. 6. |
|
|
|
118. |
|
|
|
119. а) 12; 24; 120. 15 км/ч |
6) 100 |
|
Тест 5. Дробные рациональные уравнения
Вариант 1 Вариант 2
1. 2
2. 4 2. 2
![]() 5. 10
5. 10 ![]()
IV. Неравенства
121. ![]()
![]()
![]() ;
9>8 , следовательно, 4 > Л;
;
9>8 , следовательно, 4 > Л;
ж) Заменим а +1 = 2b на равенство а —Ь = Ь —1 . По условию Ь > 1 , следовательно, b—1>0, a—b>0, а >Ь;
![]()
и) Равенство Ь+с = 2+b2 заменим на 2+b2 —Ь ; а —Ь = b 2 —2b +1+1 ; a—b=(b—1)2+1; 20; +1>0; a—b>O; а >Ь.
13 12
122. ![]()
![]() в) ¯
12 3242 ¯1; 3242 -1<3242 ;
323-325 <3242 ,
в) ¯
12 3242 ¯1; 3242 -1<3242 ;
323-325 <3242 ,
= 47-101;
;
47-101>47-99 ; 742 -272 > 732 -262 .
123. а) Составим и упростим разность
(а —1)(а+2)—(а+4)(а—З) = а2 —а +2а —2—а2 + За —4а+12 = 10 ; 10>0 ;
![]()
в) b2 +5> 2b+3 ;
г) а4 +1—2alal = а4 —2alal+1;
При а 20, lal=a, а4 —2alal+1=a4 ![]() —1)
20.
—1)
20.
ПРИ а < О, = —а , а4 —2alal+1=a4 ![]() =
а4 +2а 2 +1 = (а2 +1) > 0.
=
а4 +2а 2 +1 = (а2 +1) > 0.
Следовательно, а —2alal+1>0 при любом значении а. а 4 +12 2alal .
д) (а—2)2 24(1—а).
![]() Ь 1 2b-b2
-1
Ь 1 2b-b2
-1 ![]() (Ь2-2Ь+1) —(b—1)2 124. в)
(Ь2-2Ь+1) —(b—1)2 124. в)![]()
В -4-1 2 ¯ 2 (b2 +1) 2(b2 +1) 2(b2 +1)
(Ь-1)2 20; -(b-1)2 до;
Ь2 +1>0; 2(b2![]()
![]() -(b-1)2 Ь 1 следовательно,__ ДО; '
— при любом значении Ь.
-(b-1)2 Ь 1 следовательно,__ ДО; '
— при любом значении Ь.
2(b2 +1)
г) а4 +16—8а—2аЗ ![]()
—
(а —8) = ![]() +2а +4) = (а —2)2 (а2 +2а+4) ;
+2а +4) = (а —2)2 (а2 +2а+4) ;
(а —2)2 20; а2 +2а+4 ; следовательно, (а —2)2 (а2 +2а+4)20 , а4 +16—8а —2аз 20,
а4 +162 8а+2а при любом значении а. а
125.
а) а +1,2 < Ь
+1,2; ![]() д)
д)![]()
З З
![]()
126. а) а и Ь > З , следовательно, а и Ь > О ;
б) а >Ь и а< —13. Следовательно, Ь < а ; а < —13, —13<0 , следовательно, Ь < 0 и а < 0 ;
![]()
г) a<0•, b<0.
127.![]()
б) a—8>b—8;
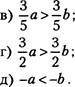
128.
а) а<0;![]()
129. а) При умножении обеих частей неравенства на отрицательное число знак неравенства
меняется.
б) Делим на положительное число, следовательно, знак неравенства не меняется.
в) Умножаем на положительное число и прибавляем одно и тоже число.
г) Умножаем обе части неравенства на отрицательное число — 0,01 и прибавляем 0,7.
д) Умножили на — 1 и прибавили 2.
![]() е) Делим на — З и
прибавляем — 4.
е) Делим на — З и
прибавляем — 4.
130. d, Ь, а, с — положительные,
![]() 1
1
d < Ь , следовательно, Ь < а
, следовательно, — > — ; а < с , следовательно, — > —![]()
![]() 1
1
Итак, — > — > — > —![]()
d b а с
Ответ: — c' a' b' d
131.
а) 24>1; ![]()
|
132. |
а) 60>12; |
б) —<6. |
|
133. |
а) 15<a+b<21; |
в) 50 < ab < 90; |
|
|
б) —10<a—b<—4; |
1 1 1 г) 5<а<6, |
15 Ь 10
134.
в) ![]() •$. Неравенства с
положительными членами можно перемножать, следовательно, 1,4• 2,2 < Уб <
1,5-2,3 , т.е. 3,08 < 3,45 .
•$. Неравенства с
положительными членами можно перемножать, следовательно, 1,4• 2,2 < Уб <
1,5-2,3 , т.е. 3,08 < 3,45 .
г) фб=ЈГ5 = 2$. Умножрп,4 второе неравенство почленно на 2,
получим ![]() итак,
итак, ![]() < 4,6.
< 4,6.
д) Умножим первое неравенство почленно на — З, получим —4,2
> ![]() > —4,5 или
> —4,5 или ![]() < -4,2.
< -4,2.
135. Рд—2а+Ь. Умножим первое неравенство почленно на 2 и сложив со вторым, получим
![]()
136. 2. 137. 1.
138.
а) Используя неравенство 2 Б, а 2 0, Ь 2 0 ; запишем ![]()
2 2 2
![]() з .
з .
Два последних неравенства почленно перемножим,
2 2
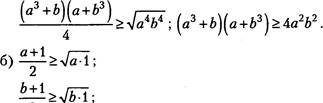
2
![]() ab•1 .
ab•1 .
2
![]() (а +1) (Ь +1) (ab+1)
(а +1) (Ь +1) (ab+1) ![]()
![]() 1
1
139. По свойству а+—22 при а , запишем два неравенства а +1+ 22, где а +1>0.
а
1
Аналогично b2 + 1+ 2 , где b2 +1 > 0. Неравенства одного знака можно складывать.
![]() 1 1
1 1
Сложив почленно неравенства,
полу-шм а +1+![]() 24, перенесем 2
24, перенесем 2
1 1
вправо и приведем подобные
слагаемые, получим а +b2 +![]() 22.
22.
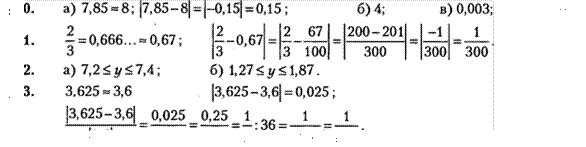
![]() • 16} .
• 16} .
60; 64; 75; 81; 90} .
148.
![]() а)
ZAOCoZDOB=ZDOC; 6) ZAOCuZDOB=ZAOB.
а)
ZAOCoZDOB=ZDOC; 6) ZAOCuZDOB=ZAOB.
149. {5; 10; 15; 20; 25; 30; 35; 40; 45; 50; ...} ,
{15; 30; 45; 60; 75; 90; 105;...} ,
Пересечение {15; 30; 45; 60; ...} ;
Объединение {5; 10; 15;20; 25; 30; 35; 40; 45; 50; 55; 60; ...}
Общая часть — множество чисел, кратных 15. 152. а) Принадлежат: — 5; — 3,9; 0; 5.
![]() б) Принадлежат: —
10; — 8; — 1,5; 0. 153. а) - 13; - 12; - 11; - 10; -9;
б) Принадлежат: —
10; — 8; — 1,5; 0. 153. а) - 13; - 12; - 11; - 10; -9;
154.
155.
156. Любое число, меньшее — 7.
157.
; 9,5) ; в)
(4; +00) ;![]()
б)
![]() 8,5) ;
8,5) ; ![]() —1,6) .
—1,6) .
|
158. |
|
-26-4); |
|
|
б) х > —33—9 или (—33—9; +00); |
|
![]() е)
(2,5; +00)
е)
(2,5; +00)![]()
-3<-2;
2x<1; х Ответ: —о.о;![]()
![]() 4—5x —1 ; —5x —5 . Ответ:
4—5x —1 ; —5x —5 . Ответ: ![]() 1) ;
1) ;
л) 3x—12>0 ; х >4. Ответ: (4;
+x)![]()
м) 2x—5<0;
2x < 5; х < 2,5. Ответ: ——2 5)![]()
н) 2x—9>0;
х >4,5; х+З#0 х #—3 . Ответ: ![]()
о) 2x+5<0; х < —2,5 ; х+4=о х
=—4. Ответ: ![]() -2,5);
-2,5);
п) х—5=О; х = 5; 4x+16<0; х <
—4. Ответ:![]() 4)u{5};
4)u{5};
р) х+2=0; х —-2 ; 2x+9>0 х >—4,5. Ответ: (—4,5; + 00 )
159.![]() -се; 1,8) ;
-се; 1,8) ;
д) —4x+3 > 0; 12x—1—12x+9 ; верно при любом значении х.
Ответ: ( оо;![]()
е) ![]() —15+3x20; 3x215; х 25 . Ответ: [5;
+сю)
—15+3x20; 3x215; х 25 . Ответ: [5;
+сю)
1 160.
![]() в)
в)
1) Если а , то —З; неверно, решений нет;
2) ![]() если а >
0, то х '
если а >
0, то х '
![]() З) если а < 0 , то х >
З) если а < 0 , то х >
Ответ: при а = 0 решений нет; при а > О хе —т,
— при а < 0 хе ![]()
![]()
![]() б) ба+Зх<1—ах ; 3x+ar<1—6a ;
(а+З)х<1—6а
б) ба+Зх<1—ах ; 3x+ar<1—6a ;
(а+З)х<1—6а
1) Если а+З=0, т.е. то 19 верно при любом значении х;
2) если а+З>О, т.е. а > —З, то х <
З) если
а+З<0 , т.е. ![]() то х >
то х >
Ответ. при а=--З,
хе ![]() ;
при а < —З
;
при а < —З![]()
![]() в) При а решений нет; д) При а = 9 при а >3, хе —о; —1)
в) При а решений нет; д) При а = 9 при а >3, хе —о; —1)![]() при
а > 9
при
а > 9
при а<З, ХЕ (—1; +00) при а <9
г) При а = —2 решений нет; е) При т = 1 решений нет;
![]() при а >—2 хе при
т >1 хе (т+1;+оо)
при а >—2 хе при
т >1 хе (т+1;+оо)![]()
при а <—2 хепри т хе —о; т +1).
162. а) Квадратное уравнение не имеет корней при D<O. D=4—4(4a+3) ; 4—4(4а+З) ;
1
1—(4а+З)<0; 1—4а—З<0; —4а<2; а >——. Ответ: при ае
—— ; + 00 ![]() 2
2
б) Имеет два корня при
![]() = -4а-2О;
= -4а-2О;
![]() — 20 > О;
— 20 > О;
в) Если а—1=0, т.е. а=1, то уравнение принимает вид
—2х+1+2—-о, -2х+3=0 ![]() х = 1,5 — одно решение.
х = 1,5 — одно решение.
Квадратное уравнение не имеет корней при 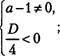 D
D
D — = а2 —(а—1)(а+2) = а2 —а2 +а—2а+2 ; 4
![]() Ответ:
при ае (2; +00) •
Ответ:
при ае (2; +00) •
163.![]()
|
164. |
а) Является. |
б) Является. |
|
165. |
4]; |
б) (1; +00). |
|
166. |
а) [-24; 24); |
6) (1; 16). |
167. а) Неравенство равносильно двум системам

ХЕ 1] Решений нет.
![]() Ответ: (—4; 1]
Ответ: (—4; 1]
б) Решается аналогично а). Сводится к решению двух систем
в) 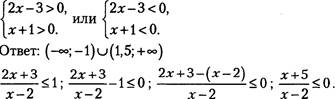
Далее смотри решение а). Ответ: [—5; 2) .
г) Аналогично в) Ответ: ( — 00) .
![]() х-5=о х-320 д) или
х-5=о х-320 д) или
х-5>0; Ответ: [5; +00) .
или
|
х = 1,5 2х-3>0; Ответ: [1,5; +00) . |
х 1,5; х 1,5 |
ж)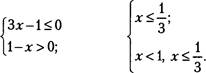
|
Ответ:
|
|
168.
![]()
![]() В) [4; -4-00)
В) [4; -4-00)![]()
169.
а) [2; 14]; ![]()
|
170. |
|
6) |
2); |
|
Тест 6. Неравенства
Вариант ![]()
|
|
2 |
|
4 |
5 |
6 |
7 |
|
8 |
|
|
З |
1 |
4 |
4 |
З |
З |
2 |
|
|
в |
|
2 |
З |
4 |
|||||||
![]() 10. [-20;
6). 11. (-13; 17) .
10. [-20;
6). 11. (-13; 17) .
12. Составим и упростим разность
![]() = а2 -2а-6а+12-а2 +5а+За-15=-З •, -З < О;
= а2 -2а-6а+12-а2 +5а+За-15=-З •, -З < О;
(а—2)(а—6)—(а—3)(а—5) (а—2)(а—6)< (а—З)(а—5) при любом значении а.
13.
4—а < 0 , следовательно, х <![]() х <4—Ф7. Ответ: —
1.
х <4—Ф7. Ответ: —
1.
Вариант 2
|
|
2 |
|
4 |
5 |
6 |
7 |
8 |
|
|
|
З |
1 |
4 |
1 |
2 |
4 |
2 |
|
|
в |
|
З |
4 |
1 |
|||||||
9. [-0,5; +![]()
12. Составим и упростим разность
![]() 2>0 ;
2>0 ;
13. 0, следовательно, х > ![]() х
> ЏА —5 . Ответ: 0.
х
> ЏА —5 . Ответ: 0.
У. Степень с целым показателем. Элементы статистики
171. а) ' 25
б)![]()
64
172. а) - 0,00001;
173.
а) ![]() б)
б)![]()
174. а)
a3b2
![]()
175. а) 16; 6) 0,25; в) 0,01;
176. а) 0,2;
в)![]()
177.
а) 9ху2![]()
б) 36х-2у- ![]() 178.
178.![]()
179. а) 6,3-107 ;
6) 3,195-106 ;
180.![]()
6) 2,8-10 см —28 см;
181. а) 1,02-106 ;
д) 25;
27 е)![]()
64 в) 6,25;
г) — 128;
в)![]()
12
г)![]()
![]() (ab2 +1) (1—a 2 b)
(ab2 +1) (1—a 2 b)
в)
г)
г) 0,25;
д) 0,2;
32
г) 2187;
д)![]()
125
в) 4х6у-14![]()
г) 3a-1 b6 ;
в) 7,5-107 ;
![]()
в) 9,73.ш-4 т;
г) 6,25-103 м; 6) 7,322-102 ;
![]()
и) 1003 = 106 =1000000.
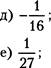 625
625
ж) 1001;
з) 101.
з) 0,04; ![]()
![]()
2187
з) 0,04;
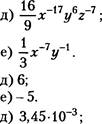 ж) 4,7-105 ;
ж) 4,7-105 ;
е) 4,7-10-6 з) 8,3-106 .
д) 3,65-104 км;
е) 7,85-1010 т.
в) 2,3646-10-4 .
Тест 7. Степень с целым показателем. Стандартный вид числа
Вариант 1
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 1, 38-10 |
|
|
|
|
|
||||||||
Вариант 2
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2,61.ш-2 |
|
|
|
|
|
||||||||
182. нет
183. Примерно 11 акций, 98 акций, 2 акции.
185. а)
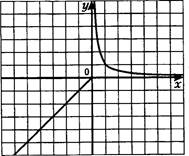 б)
б) 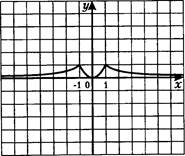
25
|
186. |
а) а=±16; |
|
|
187. |
19 а) |
68 б) |
Тест 8. Итоговый Вариант 1

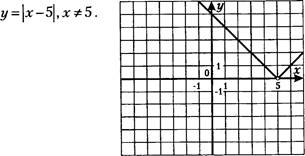
![]() 10.
10.
![]() Вариант 2
Вариант 2
|
|
|
|
|
|
|
|
|
|
10 |
11 |
|
|
|
|
|
|
|
|
|
|
|
х— 2у |
12. у =
[х + 21, х * —2 . 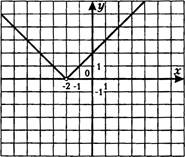
13.![]()
3aMe7
Для заметок
![]()
Отпечатано с готовых диапозитивов в фю1иале ГУП МО «КГ» «Воскресенская типография»
140200, г. Воскресенск Московской области, ул. Вовальная, д. 30 E-mail: vosprint@mail.ru тел.: 8 (49644) 2-4542 Заказ N2 989
[1] 2) ХЗ +Х —Х— 1; 4) (3a+b)2 (b—3a)2,
[2] х2 -2 9+443 9-443+( 9-4$) 2
х -2;
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.