Algebraik kasrlar. Kasrlarni qisqartisrish

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                   

                                    Zarafshon

Sana :

Fan :  Algebra

Sinf :

 

         Mavzu:  Algebraik kasr. Kasrlarni qisqartirish.

 

Darsning shiori:

                A`lo mamlakatning a`lo farzandi.

                Bilib qo`yki seni Vatan kutadi.

                                                                    (G`. G`ulom)

 

Darsning maqsadi:

a)     Tarbiyaviy: O`quvchilarni o`zaro hamkorlik, hurmat, faollik, ishchanlik, tartiblilik va madaniyatlilikka o`rgatish;

b)    Ta`limiy maqsad: Algebraik kasr. Kasrlar ustida asosiy amallarni, bajarish va ularni qisqartirishni o`rgatish, algebraik ifodalarni ko`paytuvchilarga ajratishning har xil yo`llarini egallash va ularni qo`llay olish to`g`risida bilim, ko`nikma, malaka hosil qilish;

c)     Rivojlantiruvchi: Tafakkur, xotira, idrok mashqi qiziqishini rivojlantirish, muloqot madaniyatiga o`rgatish;

d)    Kasbga yo`llovchi: Tadbirkor, vositachi, hisobchi kasblarining ayrim qirralari bilan tanishtirish;

e)     Milliy va mafkuraviy : Milliy qadriyatlar , san`at, ulug` mutafakkirlarni matematika rivojiga qo`shgan hissalaridan g`ururlanish, vatanni sevish va o`z yurtidan g`ururlanish tuyg`usini shakllantirishdan iborat.

 

Dars jihozi: Darslik , dars uchun zarur ko`rgazmali qurollar, testlar, tarqatma materiallar, kompyuter, plakatlar, doska, bo`r.

Dars usuli: Interfaol.

Dars tipi: Yangi bilim va tushunchalarni hosil qilish.

 

                    

                   Darsning bosqichlari va vaqt taqsimoti:

 

1	Tashkiliy qism	2 daqiqa
2	Yangi mavzuni yoritish a) Tayyorgarlik b) Guruglarda ishlash d) Xulosa	15 daqiqa 10 daqiqa 3 daqiqa
3	Yangi mavzuni mustahkamlash	10 daqiqa
4	Darsga yakun yasash va baholash	3 daqiqa
5	Uyga vazifa	2 daqiqa

 

Tashkiliy qism: O`quvchilar bilan salomlashish. Davomatni tekshirish. Zarur va ko`rgazmali qurollarni va jihozlarni darsga hozirlash. O`quvchilarni guruhlarga ajratish.

O`tilganlarni takrorlash va yangi mavzuga hozirlik ko`rish.

 

O`qituvchi: O`quvchilar har bir guruhga o`tilgan mavzu yuzasidan savol beraman, bir o`quvchi og`zaki ta`rifni aytadi, guruhdagi qolgan o`quvchilar esa misol yozadi.

 

I-guruhga savol: Bir had deb nimaga aytiladi?

Javob: Son va harfiy ko`paytuvchilar ko`paytmasidan iborat algebraic ifoda bir had deyiladi.

Misol: 4abc,   -3ab

II-guruhga savol: Ko`p had deb nimaga aytiladi?

Javob: Bir nechta bir hadlarning algebraik yig`indisi ko`p had deyiladi.

Misol: 2a³ +3ab+b²,         2a³-ab

III-guruhga savol: Ayirmaning kvadrati nimaga teng?

Javob: Ikki son ayirmasining kvadrati birinchi son kvadrati ayiruv birinchi son bilan ikkinchi son ko`paytmasining ikkilangani, qo`shuv ikkinchi son kvadratiga teng.

Misol: (x-y)²= x²-2xy+y²

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

O`qituvchi: O`quvchilar kompyuter ekraniga qarang ekranda misollar paydo bo`ladi. Albatta har bir guruh uchun.

I.                 1. (x+y)² =

2. (90-1)²=

   II.    1. (y-6)²=

           2. (40+1)²=

   III.    1. (m-2)²=

            2. (100-1)² =

 

O`qituvchi: Javobi esa kompyuter ekranidagi gullar bargiga yozilgan. To`g`ri noto`g`riligini tekshiring va guruh boshliqlari natijalarni e`lon qiling.

       

            

                                      Javoblar: 

I.                 1. (x+y)² =x²+2x+1        2. (90-1)²= 90²-2*90+1²=7921

   II.    1. (y-6)²=y²-12x+36     2. (40+1)²= 40²+2*40+1²=1681

   III.    1. (m-2)²= m²-4m+4      

            2. (100-1)² = 100²-2*100+1=9801

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

O`qituvchi: O`quvchilar gullar qanchalik tabiat va tabobat uchun foydali ekanligini bilasiz va gullar insonlarga estetik zavq va quvonch bag`ishlaydi.

        O`quvchilar endi men sizlardan  matematik diktant olaman xuddi ona tilidagidek ,og`zaki aytaman sizlar esa yozib misolni yechasizlar.

I-guruhga savol:  Ko`paytuvchilarga ajrating.

         1. X²-36=

II-guruhga savol:      4a²-9=

III-guruhga savol:     81a²-16b²=

Javoblar :

1)   X²-36= (x-6) (x+6)     

    2) 4a²-9= (2a-3) (2a+3)

    3) 81a²-16b²= (9a-4b) (9a+4b)

 

O`qituvchi: O`quvchilar bugun o`tilgan mavzular yuzasidan savol-javob va misollarni yechishda har bir guruh yaxshi natijalar ko`rsatdi, albatta bundan xursand bo`ldim.

O`quvchilar bugungi darsimizning maqsadi, algebraik kasr, kasrlarni qisqartirish haqida ma`lumot berishdan iborat.

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1-masala. Katerning turg`un suvdagi tezligi soatiga a kilometrga, daryo oqimining tezligi soatiga b kilometrga teng. Katerning daryo oqimi bo`yicha harakat tezligi uning daryo oqimiga qarshi harakat tezligidan necha marta ortiq?

        - Katerning daryo oqimi bo`yicha tezligi soatiga (a+b) kilometrga teng; oqimga qarshi tezligi soatiga (a-b) kilometrga teng. Shuning uchun daryo oqimi bo`yicha harakat tezligi oqimga qarshi harakat tezligidan.

 

 

 

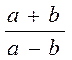marta ortiq bo`ladi.

 

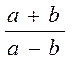                      Ifoda algebraic kasr deyiladi. Bu kasrning surati a+b,

 

maxraji esa a-b.

        Umuman ,surat va maxraji algebraik ifodalar bo`lgan kasr algebraik kasr deyiladi.

        Algebraik kasrlarga doir yana bir necha misollar keltiramiz:

 

             

 

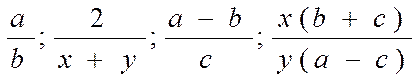
Agar algebraik kasrga kiruvchi harflar o`rniga biror sonlar qo`yilsa, u holda zarur hisoblashlar bajarilgandan keyin shu algebraic kasrning son qiymati hosil bo`ladi.

        Masalan, a=10,  b=8 bo`lganda                 algebraic kasrning son

 

qiymati 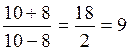         ga teng bo`ladi.

 

            algebraik kasrda a va b o`rniga o`zaro teng bo`lmagan

 

(a ≠   b) istalgan sonlarni qo`yish mumkin, chunki a=b bo`lganda kasrning maxraji nolga aylanadi, nolga bo`lish esa mumkin emas.

        Bundan keyin algebraic kasrga kiruvchi harflar yo`l qo`yiladigan qiymatlarnigina, ya`ni shu kasrning maxraji nolga teng bo`lmaydigan qiymatlarnigina qabul qiladi.

        Masalan,                  kasr uchun joiz qiymatlar a ning a=0   va    a=1 dan boshqa barcha qiymatlari bo`ladi.

Kasrning asosiy xosssasini bunday yozish mumkin:

 

                             

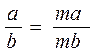
bu yerda       (b ≠ 0)      ,     (m ≠ 0)           .

        Bu xossa kasrning surat va maxrajini bir xil algebraik ifodaga ko`paytirilsa yoki bo`linsa, unga teng kasr hosil bo`lishini bildiradi, masalan:

 

 

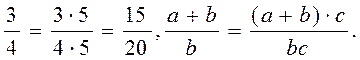
        Kasrning asosiy xossasidan foydalanib, algebraik kasrni surat va maxrajga bir vaqtda kiruvchi umumiy ko`paytuvchiga qisqartirish mumkin, masalan:

 

 

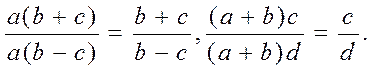
        Kasrlarni soddalashtirish uchun avval ularning surat va maxrajining umumiy ko`paytuvchisini ajratib olish kerakligiga doir misollar keltiramiz.

        2-masala.   Kasrlarni qisqartiring:

1) 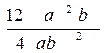                   2)

 

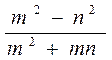
1)  12a²b  va   4ab² birhadlar 4 ab umumiy ko`paytuvchiga ega. Kasrning surat va maxrajini 4ab gab o`lamiz:

 

           

 

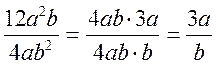
2).m²-n² va m²+mn ko`phadlar m+n umumiy ko`paytuvchiga ega, chunki m²-n²=(m+n) (m-n), m²+mn=m(m+n). Kasrning surat va maxrajini m+n ga bo`lamiz:

 

   

 

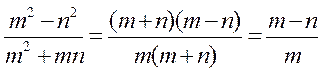Shunday qilib , kasrlarni qisqartirish uchun bu kasrlarning surat va maxrajini ularning umumiy ko`paytuvchisiga bo`lish kerak.

        Agar  kasrning surat yoki maxrajidagi ishorani qarama-qarshisiga o`zgartirilsa, u holda berilgan kasrga qarama-qarshi kasr hosil bo`lishini ta`kidlab o`tamiz:

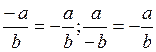
Masalan,                  .

 

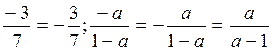3-masala. 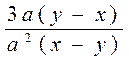                         kasrni qisqartiring.

 

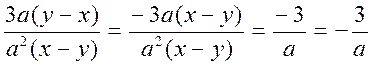
                     Mustahkamlash uchun mashqlar:

452. Surati x va y sonlarning ko`paytmasiga, maxraji esa ularning yig`indisiga teng algebraik kasrni yozing.

Javob:

453. Surati p va q sonlarning ayirmasiga, maxraji esa ularning ko`paytmasiga teng bo`lgan algebraik kasrni yozing.

Javob:

454. Surati a va b sonlar kvadratlarining ayirmasiga, maxraji esa shu sonlar ayirmasining kvadratiga teng bo`lgan algebraik kasrni yozing.

Javob:

455. Surati c va d sonlar kublarining yig`indisiga, maxraji esa shu sonlar ko`paytmasining ikkilanganiga teng bo`lgan algebraik kasrni yozing.

Javob: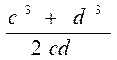

 

O`qituvchi: O`quvchilar yangi mavzuni  mustahkamlash uchun “To`g`ri soz tuzish” o`yinini o`tkazamiz. Bu o`yinda  “MATEMATIKA” so`zi hosil bo`lishi kerak. Agar misollarda xatoliklar bo`lsa harflar tushib qoladi va so`z to`g`ri emas deb hisoblanadi.

 

456 –misol.

I.       bunda  b=1,5                    J: 5

 

II.    bunda a=16,  b=-3             J: 1,9

 

III.      bunda  a=3,   b=-4         J: 4

 

 

457-misol.  I.  1) S=νt formuladan ν ni toping.     Javob: V=

                   II.   2) Р=   formuladan V ni toping  

                                                                               Javob: V=                               

                         

                     III.      3) Р= 2(a+b) formuladan a  ni toping.

                                                                              Javob:    

 

460-misol.  Berilgan ikki kasrning tengligini ko`rsating.

I.  1) 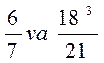                  Yechish: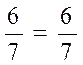 

 

II.   3)                Yechish    

 

III.   5) 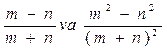   Yechish: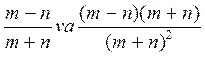   

                                                                   

 

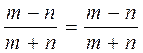
O`qituvchi: O`quvchilar qiziqarli savol javob o`yinini o`tkazamiz.

1) Al-Xorazmiy asos solgan fan.                  ( Algebra)

2) Eng kichik tup son.                                   (ikki)

3) Konstututsiya qabul qilingan sana.           (1992-yil 8-dekabr)

4) Birning ikkiga bo`linmasi.                        (yarim)

5) 2008 –yil qanday yil deb e`lon qilindi.      (Yoshlar yili)

6) Yoyiq burchak necha gradusga teng .        (180⁰)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

O`qituvchi: O`quvchilar bugungi darsdan maqsadimiz algebraik kasrlar, kasrlar ustida asosiy amallarni bajarish va ularni qisqartirishni o`rganish, algebraik ifodalarni ko`paytuvchilarga ajratishning har xil yo`llarini egallash va ularni qo`llay olishga o`rgatishdan iborat edi. Darsimiz davomida yechilgan misollardan ayon bo`ldiki, ko`zlagan maqsadimizga erishdik.

        Aziz o`quvchilar sizlardan albatta, kelajakda yurtimiz, vatanimiz ravnaqi yo`lida o`z bilimini ayamaydigan ajoyib tadbirkorlar, bank xodimlari va muhandislar chiqadi degan umiddaman.

 

Uyga vazifa:  458-misol va 456-misolning 1, 3 lari.

 

        Dars so`ngida o`quvchilar baholandi va baholar kundalikka qo`yildi.

 

 

 

 

 

 

 

Sana : ______

Fan :  Algebra

Sinf : ______

 

         Mavzu:  Algebraik kasr. Kasrlarni qisqartirish.

 

Darsning shiori:

                A`lo mamlakatning a`lo farzandi.

                Bilib qo`yki seni Vatan kutadi.

                                                                    (G`. G`ulom)

 

Darsning maqsadi:

f)      Tarbiyaviy: O`quvchilarni o`zaro hamkorlik, hurmat, faollik, ishchanlik, tartiblilik va madaniyatlilikka o`rgatish;

g)    Ta`limiy maqsad: Algebraik kasr. Kasrlar ustida asosiy amallarni, bajarish va ularni qisqartirishni o`rgatish, algebraik ifodalarni ko`paytuvchilarga ajratishning har xil yo`llarini egallash va ularni qo`llay olish to`g`risida bilim, ko`nikma, malaka hosil qilish;

h)    Rivojlantiruvchi: Tafakkur, xotira, idrok mashqi qiziqishini rivojlantirish, muloqot madaniyatiga o`rgatish;

i)       Kasbga yo`llovchi: Tadbirkor, vositachi, hisobchi kasblarining ayrim qirralari bilan tanishtirish;

j)       Milliy va mafkuraviy : Milliy qadriyatlar , san`at, ulug` mutafakkirlarni matematika rivojiga qo`shgan hissalaridan g`ururlanish, vatanni sevish va o`z yurtidan g`ururlanish tuyg`usini shakllantirishdan iborat.

 

Dars jihozi: Darslik , dars uchun zarur ko`rgazmali qurollar, testlar, tarqatma materiallar, kompyuter, plakatlar, doska, bo`r.

Dars usuli: Interfaol.

Dars tipi: Yangi bilim va tushunchalarni hosil qilish.

 

                   

                   Darsning bosqichlari va vaqt taqsimoti:

 

1	Tashkiliy qism	2 daqiqa
2	Yangi mavzuni yoritish a) Tayyorgarlik b) Guruglarda ishlash d) Xulosa	15 daqiqa 10 daqiqa 3 daqiqa
3	Yangi mavzuni mustahkamlash	10 daqiqa
4	Darsga yakun yasash va baholash	3 daqiqa
5	Uyga vazifa	2 daqiqa

 

Tashkiliy qism: O`quvchilar bilan salomlashish. Davomatni tekshirish. Zarur va ko`rgazmali qurollarni va jihozlarni darsga hozirlash. O`quvchilarni guruhlarga ajratish.

O`tilganlarni takrorlash va yangi mavzuga hozirlik ko`rish.

 

O`qituvchi: O`quvchilar har bir guruhga o`tilgan mavzu yuzasidan savol beraman, bir o`quvchi og`zaki ta`rifni aytadi, guruhdagi qolgan o`quvchilar esa misol yozadi.

 

I-guruhga savol: Bir had deb nimaga aytiladi?

Javob: Son va harfiy ko`paytuvchilar ko`paytmasidan iborat algebraic ifoda bir had deyiladi.

Misol: 4abc,   -3ab

II-guruhga savol: Ko`p had deb nimaga aytiladi?

Javob: Bir nechta bir hadlarning algebraik yig`indisi ko`p had deyiladi.

Misol: 2a³ +3ab+b²,         2a³-ab

III-guruhga savol: Ayirmaning kvadrati nimaga teng?

Javob: Ikki son ayirmasining kvadrati birinchi son kvadrati ayiruv birinchi son bilan ikkinchi son ko`paytmasining ikkilangani, qo`shuv ikkinchi son kvadratiga teng.

Misol: (x-y)²= x²-2xy+y²

 

O`qituvchi: O`quvchilar kompyuter ekraniga qarang ekranda misollar paydo bo`ladi. Albatta har bir guruh uchun.

II.             1. (x+y)² =

2. (90-1)²=

   II.    1. (y-6)²=

           2. (40+1)²=

   III.    1. (m-2)²=

            2. (100-1)² =

 

O`qituvchi: Javobi esa kompyuter ekranidagi gullar bargiga yozilgan. To`g`ri noto`g`riligini tekshiring va guruh boshliqlari natijalarni e`lon qiling.

       

            

                                      Javoblar: 

II.             1. (x+y)² =x²+2x+1        2. (90-1)²= 90²-2*90+1²=7921

   II.    1. (y-6)²=y²-12x+36     2. (40+1)²= 40²+2*40+1²=1681

   III.    1. (m-2)²= m²-4m+4      

            2. (100-1)² = 100²-2*100+1=9801

 

O`qituvchi: O`quvchilar gullar qanchalik tabiat va tabobat uchun foydali ekanligini bilasiz va gullar insonlarga estetik zavq va quvonch bag`ishlaydi.

        O`quvchilar endi men sizlardan  matematik diktant olaman xuddi ona tilidagidek ,og`zaki aytaman sizlar esa yozib misolni yechasizlar.

I-guruhga savol:  Ko`paytuvchilarga ajrating.

         1. X²-36=

II-guruhga savol:      4a²-9=

III-guruhga savol:     81a²-16b²=

Javoblar :

2)   X²-36= (x-6) (x+6)      

    2) 4a²-9= (2a-3) (2a+3)

    3) 81a²-16b²= (9a-4b) (9a+4b)

 

O`qituvchi: O`quvchilar bugun o`tilgan mavzular yuzasidan savol-javob va misollarni yechishda har bir guruh yaxshi natijalar ko`rsatdi, albatta bundan xursand bo`ldim.

O`quvchilar bugungi darsimizning maqsadi, algebraik kasr, kasrlarni qisqartirish haqida ma`lumot berishdan iborat.

       

1-masala. Katerning turg`un suvdagi tezligi soatiga a kilometrga, daryo oqimining tezligi soatiga b kilometrga teng. Katerning daryo oqimi bo`yicha harakat tezligi uning daryo oqimiga qarshi harakat tezligidan necha marta ortiq?

        - Katerning daryo oqimi bo`yicha tezligi soatiga (a+b) kilometrga teng; oqimga qarshi tezligi soatiga (a-b) kilometrga teng. Shuning uchun daryo oqimi bo`yicha harakat tezligi oqimga qarshi harakat tezligidan.

 

 

 

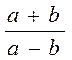marta ortiq bo`ladi.

 

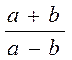                      Ifoda algebraic kasr deyiladi. Bu kasrning surati a+b,

 

maxraji esa a-b.

        Umuman ,surat va maxraji algebraik ifodalar bo`lgan kasr algebraik kasr deyiladi.

        Algebraik kasrlarga doir yana bir necha misollar keltiramiz:

 

             

 

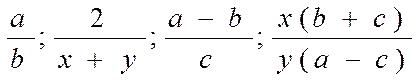
Agar algebraik kasrga kiruvchi harflar o`rniga biror sonlar qo`yilsa, u holda zarur hisoblashlar bajarilgandan keyin shu algebraic kasrning son qiymati hosil bo`ladi.

        Masalan, a=10,  b=8 bo`lganda                 algebraic kasrning son

 

qiymati 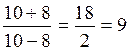         ga teng bo`ladi.

 

            algebraik kasrda a va b o`rniga o`zaro teng bo`lmagan

 

(a ≠   b) istalgan sonlarni qo`yish mumkin, chunki a=b bo`lganda kasrning maxraji nolga aylanadi, nolga bo`lish esa mumkin emas.

        Bundan keyin algebraic kasrga kiruvchi harflar yo`l qo`yiladigan qiymatlarnigina, ya`ni shu kasrning maxraji nolga teng bo`lmaydigan qiymatlarnigina qabul qiladi.

        Masalan,                  kasr uchun joiz qiymatlar a ning a=0   va    a=1 dan boshqa barcha qiymatlari bo`ladi.

Kasrning asosiy xosssasini bunday yozish mumkin:

 

                             

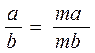
bu yerda       (b ≠ 0)      ,     (m ≠ 0)           .

        Bu xossa kasrning surat va maxrajini bir xil algebraik ifodaga ko`paytirilsa yoki bo`linsa, unga teng kasr hosil bo`lishini bildiradi, masalan:

 

 

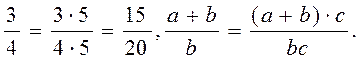
        Kasrning asosiy xossasidan foydalanib, algebraik kasrni surat va maxrajga bir vaqtda kiruvchi umumiy ko`paytuvchiga qisqartirish mumkin, masalan:

 

 

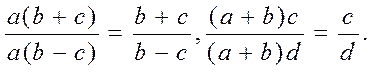
        Kasrlarni soddalashtirish uchun avval ularning surat va maxrajining umumiy ko`paytuvchisini ajratib olish kerakligiga doir misollar keltiramiz.

        2-masala.   Kasrlarni qisqartiring:

1) 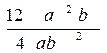                   2)

 

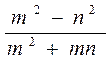
2)  12a²b  va   4ab² birhadlar 4 ab umumiy ko`paytuvchiga ega. Kasrning surat va maxrajini 4ab gab o`lamiz:

 

           

 

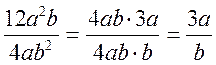
2).m²-n² va m²+mn ko`phadlar m+n umumiy ko`paytuvchiga ega, chunki m²-n²=(m+n) (m-n), m²+mn=m(m+n). Kasrning surat va maxrajini m+n ga bo`lamiz:

 

   

 

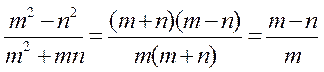Shunday qilib , kasrlarni qisqartirish uchun bu kasrlarning surat va maxrajini ularning umumiy ko`paytuvchisiga bo`lish kerak.

        Agar  kasrning surat yoki maxrajidagi ishorani qarama-qarshisiga o`zgartirilsa, u holda berilgan kasrga qarama-qarshi kasr hosil bo`lishini ta`kidlab o`tamiz:

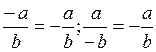
Masalan,                  .

 

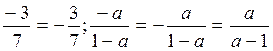3-masala. 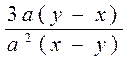                         kasrni qisqartiring.

 

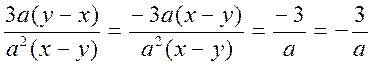
                     Mustahkamlash uchun mashqlar:

452. Surati x va y sonlarning ko`paytmasiga, maxraji esa ularning yig`indisiga teng algebraik kasrni yozing.

Javob:

453. Surati p va q sonlarning ayirmasiga, maxraji esa ularning ko`paytmasiga teng bo`lgan algebraik kasrni yozing.

Javob:

454. Surati a va b sonlar kvadratlarining ayirmasiga, maxraji esa shu sonlar ayirmasining kvadratiga teng bo`lgan algebraik kasrni yozing.

Javob:

455. Surati c va d sonlar kublarining yig`indisiga, maxraji esa shu sonlar ko`paytmasining ikkilanganiga teng bo`lgan algebraik kasrni yozing.

Javob: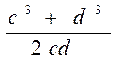

O`qituvchi: O`quvchilar yangi mavzuni  mustahkamlash uchun “To`g`ri soz tuzish” o`yinini o`tkazamiz. Bu o`yinda  “MATEMATIKA” so`zi hosil bo`lishi kerak. Agar misollarda xatoliklar bo`lsa harflar tushib qoladi va so`z to`g`ri emas deb hisoblanadi.

 

456 –misol.

I.       bunda  b=1,5                    J: 5

 

II.    bunda a=16,  b=-3             J: 1,9

 

III.      bunda  a=3,   b=-4         J: 4

 

457-misol.  I.  1) S=νt formuladan ν ni toping.     Javob: V=

                   II.   2) Р=   formuladan V ni toping 

                                                                               Javob: V=                               

                         

                     III.      3) Р= 2(a+b) formuladan a  ni toping.

                                                                              Javob:    

460-misol.  Berilgan ikki kasrning tengligini ko`rsating.

I.  1) 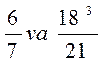                  Yechish: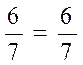 

 

II.   3)                Yechish    

 

III.   5) 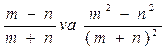   Yechish: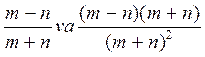   

                                                                   

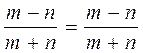
O`qituvchi: O`quvchilar qiziqarli savol javob o`yinini o`tkazamiz.

1) Al-Xorazmiy asos solgan fan.                  ( Algebra)

2) Eng kichik tup son.                                   (ikki)

3) Konstututsiya qabul qilingan sana.           (1992-yil 8-dekabr)

4) Birning ikkiga bo`linmasi.                        (yarim)

5) 2019 –yil qanday yil deb e`lon qilindi.     

6) Yoyiq burchak necha gradusga teng .        (180⁰)

O`qituvchi: O`quvchilar bugungi darsdan maqsadimiz algebraik kasrlar, kasrlar ustida asosiy amallarni bajarish va ularni qisqartirishni o`rganish, algebraik ifodalarni ko`paytuvchilarga ajratishning har xil yo`llarini egallash va ularni qo`llay olishga o`rgatishdan iborat edi. Darsimiz davomida yechilgan misollardan ayon bo`ldiki, ko`zlagan maqsadimizga erishdik.

        Aziz o`quvchilar sizlardan albatta, kelajakda yurtimiz, vatanimiz ravnaqi yo`lida o`z bilimini ayamaydigan ajoyib tadbirkorlar, bank xodimlari va muhandislar chiqadi degan umiddaman.

 

Uyga vazifa:  458-misol va 456-misolning 1, 3 lari.

 

        Dars so`ngida o`quvchilar baholandi va baholar kundalikka qo`yildi.