Answers - Worksheet A

1                         9, 13, 17, 21, 25         b 4, 9, 16, 25, 36          c 2, 4, 8, 16, 32            d  ,  ,  ,  ,  

           e −1, 4, 21, 56, 115      f       ,  , 0, − , −       g  ,  ,  ,  ,          h 16, 8, 4, 2, 1

           d  × 2ⁿ                                   e 33 − 11n                                f (n − 1)³

           g n² + 3                                   h   ⁿ                                   i 2ⁿ − 1

2                         1n+

4                a u₃ = c + 3 = 11  ∴ c = 8

b      u₆ = 8 + 3⁴ = 89

5                a u₄ = 4(8 + k) = 32 + 4k             u₆ = 6(12 + k) = 72 + 6k            ∴ 72 + 6k = 2(32 + 4k) − 2

                    72 + 6k = 62 + 8k

                    k = 5

b      u_n = n(2n + 5) = 2n² + 5n     u_{n − 1} = (n − 1)[2(n − 1) + 5] = (n − 1)(2n + 3) = 2n² + n − 3

              ∴ u_n − u_{n − 1} = (2n² + 5n) − (2n² + n − 3) = 4n + 3

6                a u₁ = k − 3         u₂ = k² − 3

            ∴ k − 3 + k² − 3 = 0                  k² + k − 6 = 0                         (k + 3)(k − 2) = 0              k = −3 or 2

b      k = −3 ⇒     u₅ = (−3)⁵ − 3 = −243 − 3 = −246

                 k = 2  ⇒         u₅ = 2⁵ − 3 = 32 − 3 = 29

7                a 3, 7, 11, 15      b 2, 7, 22, 67

          c −2, 1, 7, 19                                                   d 5, 2, 5, 2

          e −1, 14, −46, 194                                            f 10, 3, 2.3, 2.23

            g 6, −1, 1 ,                                                   h 0,  ,  ,  

           d u_n+1 =  u_n,  u₁ = 120              e u_n+1 = 2u_n + 1,  u₁ = 4             f u_n+1 = 4u_n − 1,  u₁ = 1

C1         SEQUENCES AND SERIES                                              Answers - Worksheet A     page 2

9                a −3 = −4a + b   b 8 = b c 4 =  a + b

            −1 = −3a + b                              4 = 8a + b                                 3 = 4a + b     

  subtracting,  2 = a  a = − , b = 8  subtracting, 1 =  a   a = 2, b = 5    a =  , b =  

10            a u₂ = 4 + 3k       b u₂ = 2k + 5

               u₃ = 4(4 + 3k) + 3k = 16 + 15k                           u₃ = k(2k + 5) + 5 = 2k² + 5k + 5

           c u₂ = 4k − k = 3k                                             d u₂ = 2 + k

               u₃ = 4(3k) − k = 11k                                         u₃ = 2 − k(2 + k) = 2 − 2k − k²

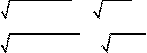           e u₂ = ⁴                                                               f u₂ = ³ 61k³ +3k³ = ³ 64k³ = 4k

k

  u₃ = ⁴ ÷ k = ⁴₂  u₃ = ³ 61k³ +64k³ = ³ 125k³ = 5k k        k

11            a u₂ =  (k + 6)    u₃ =  [k +  (k + 6)] =  (5k + 18)        b  (5k + 18) = 7          k = 2

               u₄ =  (2 + 21) = 11

12            a u₄ = 30 − 2 = 28           b u₄ =  + 2 = 5

               10 = 3u₂ − 2  ∴ u₂ = 4                                       5 =  u₂ + 2  ∴ u₂ = 4

               4 = 3u₁ − 2  ∴ u₁ = 2                                        4 =  u₁ + 2  2       

           c u₄ = 0.2 × 1.2 = 0.24                                      d u

             −0.2 = 0.2(1 − u₂)  ∴ u₂ = 2                                 1 =  = 4

               2 = 0.2(1 − u₁)  ∴ u₁ = −9                                  4 =  = 64

13            a u₅ = 2 + 4c = 30  ∴ c = 7

b      sequence is  2, 9, 16, 23, 30, …

               ∴ u_n = 7n − 5

14            a u₂ = 3(−4 − k) = −12 − 3k                    u₃ = 3[(−12 − 3k) − k] = −36 − 12k

b      −36 − 12k = 7(−12 − 3k) + 3

            9k = −45          k = −5

c      u₃ = −36 + 60 = 24  ∴ u₄ = 3(24 + 5) = 87

15            a t₂ = 1.5k + 2

               t₃ = k(1.5k + 2) + 2 = 1.5k² + 2k + 2

b      1.5k² + 2k + 2 = 12

 3k² + 4k − 20 = 0  (3k + 10)(k − 2) = 0  k = −3 , 2

Answers - Worksheet B

2                a a = 7, d = 2      b a =  , d =    c a = 17, d = −8

                        u_n = 7 + 2(n − 1) = 5 + 2n                     u_n =               +  (n − 1) = − +  n     u_n = 17 − 8(n − 1) = 25 − 8n  

3                a a = 8, d = 4, n = 30       b a = 60, d = −7, n = 30            c a = 7 , d = 1 , n = 30

               S₃₀ =  [16 + (29 × 4)]              S₃₀ =  [120 + (29 × −7)]          S₃₀ =  [14 + (29 × 1 )]

4                a S₂₀ =  (60 + 136)       b S₃₂ =  (100 + 84.5) c S₁₇ =  [28 + (−20)]

5                a S₄₈ =  [4 + (47 × 9)]   b S₃₆ =  [200 + (35 × −5)]      c S₅₅ =  [38 + (54 × 13)]

               S₂₀ =  (8 + 65)                        S₁₈ =  (3.4 + 23.8)                  S₃₂ =  [22 + (−226)]

               ∴ d = 3                                                              S₃₅ =  [46 + (34 × 7)] = 4970

b      S₄₀ =  [42 + (39 × 3)] = 3180

c      u₄₀ = 2 + (39 × 11) = 431                                                                             b S₂₅ =  [172 + (24 × −7)] = 50

11        a a + 4d = 23  (1)                                         12       a S_n = 1 + 2 + 3 + … + (n − 1) + n

                (2a + 9d) = 240  ⇒  2a + 9d = 48                        write in reverse

              2 × (1)                    ⇒  2a + 8d = 46                        S_n = n + (n − 1) + … + 3 + 2 + 1

               subtracting, d = 2                                                     adding, 2S_n = n × (n + 1)

            sub.                  a = 15                                                                                                                                       S_n =  n(n + 1)   b S₆₀ =  [30 + (59 × 2)] = 4440                                               b = S₁₀₀ − S₂₉

                                                                                              =  × 100 × 101 −  × 29 × 30

                                                                                              = 5050 − 435 = 4615

C1         SEQUENCES AND SERIES                                              Answers - Worksheet B     page 2

13            a 5 + 7 + 9 + 11 + 13                       b 15 + 12 + 9 + 6 + 3 + 0 − 3 − 6 − 9

c       15 + 19 + 23 + 27 + 31 + 35 + 39

d       4 + 4 + 3 + 3 + 2 + 2 + 1 + 1

14            a AP:  a = 4, b AP:  a = 88, c AP:  a = 19, d AP:  a = 3,   l = 61, n = 20  l = 0, n = 45  l = 127, n = 28  l = 13, n = 41

                        S₂₀ =  (4 + 61)                       S₄₅ =  (88 + 0)                        S₂₈ =  (19 + 127)        S₄₁ =  (3 + 13)                                        = 650                                                     = 1980                                                = 2044                                                    = 328

15            AP:  a = −2, l = 4n − 6                                                                            16        a AP:  a = 2, l = 160, n = 80

           S_n =  6)] = 720                                         S₈₀ =  (2 + 160) = 6480

            ∴ n(4n − 8) = 1440                                                                                                      b AP:  a = 3, l = 198, n = 66          n² − 2n − 360 = 0                                                                                                           S₆₆ =  (3 + 198) = 6633          (n + 18)(n − 20) = 0                                                                                c AP:  a = 30, l = 300, d = 6

           n > 0  ∴ n = 20                                                             30 + 6(n − 1) = 300  ∴ n = 46

                                                                                               S₄₆ =  (30 + 300) = 7590

17       a a + (9 × −11) = 101                                   18       a a = 17,  17 + 4d = 27  ∴ d = 2.5

a      = 200                                                                                                                                              b 17 + 2.5(r − 1) = 132

b      S₃₀ =  [400 + (29 × −11)] = 1215                                                  r = 47

c      S₄₇ =  (17 + 132) = 3501.5

19        a  (2a + 5d) = 213  ⇒   2a + 5d = 71    20        a S₈ = (2 × 8²) + (5 × 8) = 168   (2a + 9d) = 295  ⇒   2a + 9d = 59                          b S₇ = (2 × 7²) + (5 × 7) = 133  subtracting, 4d = −12                                                                                        u₈ = S₈ − S₇ = 35                                                 d = −3                                                                                                 c S_{n − 1} = 2(n − 1)² + 5(n − 1)  sub.                  a = 43                                                                                                                            = 2n² + n − 3

b      43 − 3(n − 1) > 0                                                                                                                 u_n = S_n − S_{n − 1}         n <  15 positive terms                                                                                           = (2n² + 5n) − (2n² + n − 3)

c      max S_n when n = 15                                                                                                                         = 4n + 3

              S₁₅ =  [86 + (14 × −3)] = 330

21       a (2k + 3) − (k + 2) = (4k − 2) − (2k + 3)     22      a 2t − (5 − t) = (6t − 3) − 2t

              k + 1 = 2k − 5                                                         3t − 5 = 4t − 3

               k = 6                                                                       t = −2

             b a = 8,  a + d = 15  ∴ d = 7                                                                 b u₅ = 7, u₆ = −4  ∴ d = −11      S₂₅ =  [16 + (24 × 7)] = 2300                                                                         a + (4 × −11) = 7  ∴ a = 51

                                                                                               S [102 + (17 × −11)] = −765

Answers - Worksheet C

1             a + 2d = −10  (1)                                      2          a a + 2d =  

             (2a + 7d) = 16  ⇒  2a + 7d = 4                                                           a + 6d = 2       2 × (1)                               ⇒  2a + 4d = −20                                                      subtracting, 4d = 1        subtracting, 3d = 24                                                                                                                                            d =                                                      d = 8                                                                                                      sub.                  a =  

            sub.                  a = −26                                                                                                b S_n = ⁿ₂ [ ¹₆ +  (n − 1)]            b −26 + 8(n − 1) > 300                                                                                                              =  n[4 + 9(n − 1)]      n >  smallest n = 42                                                                                 =  n(9n − 5)              [ k =  ]

3         a  (2a + 8d) = 126                                      4        a (5k + 3) − (7k − 1) = (4k + 1) − (5k + 3)

              9(a + 4d) = 126                                                    −2k + 4 = −k − 2

a        + 4d = 14                                                                                                                                        k = 6

b         (2a + 14d) = 277.5                                                                                              b given terms = 41, 33, 25

              a + 7d = 18.5                                                           d = −8

               subtracting, 3d = 4.5                                               smallest +ve term = 25 + (3 × −8) = 1

                                  d = 1.5                                             c consider series of +ve terms in reverse

              sub.              a = 8                                                    a = 1, d = 8

c        S₃₂ =  [16 + (31 × 1.5)] = 1000                                                     S_r = ₂^r [2 + 8(r − 1)] = r(4r − 3)

               S (4 + 120) = 1860                                    b AP:  a = 500, d = 40

                   = (2 × 1860) − 150 = 3570                                 S_n =  1)] = 10n(3n + 37)

                                                                                                                                                                                                  ∴ 20n(n + 24) = 10n(3n + 37)                                                                                                                                                                                                   n ≠ 0 ∴ 2(n + 24) = (3n + 37)

                                                                                                              n = 11  ∴ 11 years

7         a S_n = 2 + 4 + 6 + … + (2n − 2) + 2n            8         a S_n = a + (n − 1)d]

               write in reverse                                                    b Sa + d

            S_n = 2n + (2n − 2) + … + 6 + 4 + 2                                                        Sa + 5d) = 6a + 15d  adding, 2S_n = n × (2n + 2)                                                                                 Sa + 7d) = 8a + 28d

               S₆₀₁ =  (200 + 800) = 300 500                                              = 8a + 28d = S₈

               integers 200 to 800 divisible by 4                        c for +ve terms     40 − 3(n − 1) > 0

               AP:  a = 200, l = 800                                                                        n <  14 terms

               200 + 4(n − 1) = 800  ⇒  n = 151                            [80 + (13 × −3)] = 287

               S₁₅₁ =  (200 + 800) = 75 500 

              required sum = 300 500 − 75 500

                                    = 225 000

C1         SEQUENCES AND SERIES                                              Answers - Worksheet C    page 2

9          a i u₄ − u₁ = x + 3                                                                                 10        Sa + 19d) = 20a + 190d                    u₇ = u₄ + (x + 3) = 3x + 6                                                                       Sa + 29d) = 30a + 435d            ii 3d = x + 3                                                                                                                    S₃₀ − S₂₀ = 10a + 245d             d =  x + 1                                                                                               ∴ 20a + 190d = 10a + 245d     iii S₁₀ =  [2x + 9(  x + 1)]                                                                    10a = 55d

                                     = 5[2x + 3x + 9] = 25x + 45                                                     2a = 11d  b x + 19(  x + 1) = 52                                                                           ∴ a : d  =  11 : 2

            3x + 19x + 57 = 156      x =  =  or 4

11         a S₆ = 12(16 − 6) = 120                                                                       12        a i        2400 + (5 × 250) = 3650  S₅ = 10(16 − 5) = 110                                                                                                  ii AP:  a = 2400, d = 250             u₆ = S₆ − S₅ = 10                                                                                                                                    S₁₀ =  [4800 + (9 × 250)]        b S_n = 2n(16 − n) = 32n − 2n²                                                                                         = 35 250          S_{n − 1} = 2(n − 1)[16 − (n − 1)]                                                    b AP:  a = 2400, d = C

                            = 2(n − 1)(17 − n)                                                                                         [4800 + (9 × C)] = 40 000                         = −2n² + 36n − 34                                                                              C =  = 356 (nearest unit)

              u_n = S_n − S_n − ₁

                   = (32n − 2n²) − (−2n² + 36n − 34)

                   = 34 − 4n

             c u_{n − 1} = 34 − 4(n − 1) = 38 − 4n         u_n − u_{n − 1} = (34 − 4n) − (38 − 4n) = −4            u_n − u_{n − 1} constant  ∴ arithmetic series

13       a let common difference be d

            S_r = a + (a + d) + (a + 2d) + … + (l − 2d) + (l − d) + l    write in reverse

              S_r = l + (l − d) + (l − 2d) + … + (a + 2d) + (a + d) + a

                adding, 2S_r = r × (a + l)

                              S_r =  r(a + l)

           b n = 18, l = 68, S₁₈ = 153

            ∴ 153 =  (a + 68)                   a = 17 − 68 = −51

Answers - Worksheet D

                                   d = 27                                                 S₂₀ =  [6 + (19 × 4)]

               sub.              a = 13                                                       = 820

          b S₂₅ =  [26 + (24 × 27)] = 8425

3          a (2t − 5) − t = 8.6 − (2t − 5)                                        4          a S_n = (n + 1)  t = 6.2                                                                                                                                       b = S₄₀₀ − S₁₉₉

b      u₁ = 6.2, u₂ = 12.4 − 5 = 7.4                                                                                     =         × 400 × 401  × 199 × 200 a = 6.2, d = 7.4 − 6.2 = 1.2                                                                              = 80 200 − 19 900 = 60 300 u₁₆ = 6.2 + (15 × 1.2) = 24.2                                                                      c          (N + 1) = 4950

c      S₂₀ =  [12.4 + (19 × 1.2)] = 352                                                     N ² + N − 9900 = 0

                                                                                               (N + 100)(N − 99) = 0

                                                                                               N > 0  ∴ N = 99

5          a u₂ = k + 1                                                                                                                   6  a AP:  a = 3, d = 3        u₃ = k + (k + 1)² = k² + 3k + 1                                                                  500 ÷ 3 =  n = 166       b k² + 3k + 1 = 1                                                                                                                         S          [6 + (165 × 3)]

               k(k + 3) = 0                                                                     = 41 583

            k ≠ 0  ∴ k = −3                                                                                                               b AP:  a = 14, l = 99, n = 18      c u₂₅ = 1                                                                                                                                                             S₁₈ =  (14 + 99)

               u₁ = 1  ⇒  u₃ = 1                                                           = 1017

               ∴ u_n = 1 for all odd values of n

7         a S_n = a + (a + d) + (a + 2d) + …                 8        t₂ = 4 + 2k

                                    + [a + (n − 2)d] + [a + (n − 1)d]                                  t₃ = 4 − k(4 + 2k)       write in reverse                                                                                                             ∴ 4 − 4k − 2k² = 3

              S_n = [a + (n − 1)d] + [a + (n − 2)d] + …                  2k² + 4k − 1 = 0

                                    + (a + 2d) + (a + d) + a                                                                         k =    adding 2S_n = n × {a + [a + (n − 1)d]}              k > 0                              S_n = a + (n − 1)d]                                                             b S       2 + (25 × 6)] = 1924                                                              

               S 2 + (26 × 6)] = 2079

               ∴ largest n = 26

9           a = 6 + (19 × 3) = 63                                                                          10        a = 3 × 570 = 1710    b S_n =  1)] = 270                                                              b = 570 + (2 × 30) = 630  ∴ n(3n + 9) = 540                                                                                                         c = 570 + (  × 30 × 31) = 1035                n² + 3n − 180 = 0                     (n + 15)(n − 12) = 0      n > 0 ∴ n = 12

C1         SEQUENCES AND SERIES                                              Answers - Worksheet D    page 2

11        a 2 years = 8 × 3 months                                                                      12        AP:  a = 80, d = −3, n = 45        total = 3 × S₈  [AP: a = 40, d = 2]                                              S₄₅ =  [160 + (44 × −3)] = 630

                      = 3 ×  [80 + (7 × 2)]

                           = 3 × 376 = £1128     b n years = 4n × 3 months  total = 3 × S_4n

                      = 3 × ⁴₂ⁿ {80 + [(4n − 1) × 2]}

                       = 6n(80 + 8n − 2)

                       = 12n(4n + 39)

13        a a + 2d = 298,  a + 7d = 263                                        14        a AP:  a = 10, d = 6  subtracting, 5d = −35                                                                                                  S_n = ⁿ₂ [20 + 6(n − 1)]

                                   d = −7                                                      = n(3n + 7)

             b sub.              a = 312                                                                                                b S_2n = 2n[(3 × 2n) + 7]           312 − 7(n − 1) > 0                                                                                                                       = 12n² + 14n    n 45 positive terms                                                                   required sum = S_2n − S_n            c max S_n when n = 45                                                                                                     = (12n² + 14n) − (3n² + 7n)

              S₄₅ =  [624 + (44 × −7)] = 7110                                 = 9n² + 7n = n(9n + 7)

15        a u₂ = k² − 2,  u₄ = k⁴ − 4                             16      a (4k − 2) − (k + 4) = (k² − 2) − (4k − 2)

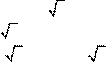            ∴ k² − 2 + k⁴ − 4 = 6                                                                                           3k − 6 = k² − 4k                       k⁴ + k² − 12 = 0                                                                                                              k² − 7k + 6 = 0                         (k² + 4)(k² − 3) = 0                                                                                 b (k − 1)(k − 6) = 0       k² = −4 [no solutions] or 3                                                                                          k = 1 or 6                      k > 0  ∴ k =    3                                                                                                                        d = 3k − 6        b u₁ =   3 − 1                                                                                                                              d > 0  ∴ k = 6

               u₃ = (   3 )³ − 3 = 3(   3 − 1) = 3u₁                           a = 10, d = 12

                                                                                              u₁₅ = 10 + (14 × 12) = 178