
January 2003PhysicsFactsheet Number
43
This Factsheet explains how charged particles, such as electrons or protons, are accelerated by two types of circular particle accelerator, the cyclotron and the synchrotron.
Circular particle accelerators bring together ideas from several different areas in physics. Reference will be made in this factsheet to ideas of centripetal forces covered in the Factsheet on uniform circular motion (19).
The cyclotron consists of:
• An evacuated chamber to minimise energy losses resulting from collisions of ions with air molecules.
• A source of charged particles that are to be accelerated – an ion source. • Two ‘dees’ across which an alternating voltage is applied that accelerates the ions when they move from one dee to the next.
• A uniform magnetic field that keeps the ions moving in a circular path and confines them to the two dees. This magnetic field is usually produced by an electromagnet.
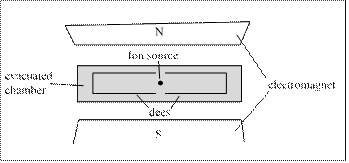
A cyclotron can be used to accelerate positively or negatively charged ions. In the following explanation the ions are considered to be positive ions.
|
F = Bqv |
B = size of magnetic field (T) q = charge on particle (C) v = speed of particle (m/s) |
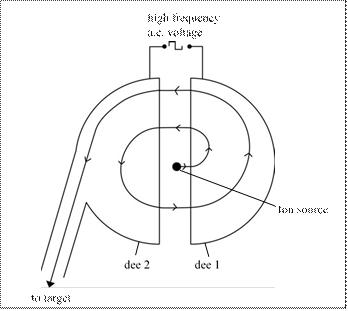
• Positive ions are released from the ion source. These positive ions are accelerated towards dee 1, which is initially given a negative potential to attract the positive ions.
• Once inside dee 1 the positive ions move at constant speed. A uniform magnetic field is applied perpendicularly to the dees by the electromagnet. This magnetic field makes the positive ions move in a circular path.
• The positive ions turn around and move towards the gap from dee 1 into dee 2.
• The alternating voltage reverses giving dee 2 a negative potential. When the positive ions cross the gap from dee 1 into dee 2 they are accelerated towards dee 2 by the negative potential.
Once inside dee 2 the positive ions have a faster speed than when they were in dee 1 - this remains constant within the dee. The above sequence of events now repeats itself. The magnetic field makes the ions move in a semi circle back to the gap between the dees at which point the alternating voltage has reversed and so the positive ions are accelerated back across the gap towards dee1, which now has a negative potential once more.
As the speed increases, the radius of the circular path followed by the ions increases but the time that the ion spends in each dee remains constant. This means that the frequency of the alternating voltage remains constant.
|
1. The constant magnetic field applied perpendicular to the dees exerts a force on the ions that makes them move in a circular path. 2. The speed inside a dee remains constant. 3. The speed of the ions increases as they move from one dee to the next. This is because they are attracted to the oppositely charge dee. 4. The ions spend an equal amount of time in each dee, as they speed up, the circular path increases in radius and they travel further in each dee. |
Exam Hint: Questions that require explanation type answers are best presented as ‘bullet points’ as shown in the explanations given about the cyclotron accelerator. They help you to order your thoughts and make it easier for the examiner to identify the important points that deserve a mark. All bullet points should remain as structured sentences as marks are also awarded on exam papers for your ‘quality of written communication.’
We will now derive an expression for the speed of the ions inside the cyclotron by applying Newton’s second law of motion, but before we do this we need to know the following:
The force exerted on a charged particle moving perpendicular through a magnetic field acts as a centripetal force, moving the particle in a circular path.
The acceleration of an object moving in a circle is given by the expression:
|
|
v = speed of object (m/s) r = radius of circular path of the object (m) |
 Further
explanation of the terms in italics and circular motion is given in The
maximum speed of the particles. For any particular ion, the maximum speed
that it can reach is limited by two factors:
Further
explanation of the terms in italics and circular motion is given in The
maximum speed of the particles. For any particular ion, the maximum speed
that it can reach is limited by two factors:
1. The radius of the cyclotron
2. The maximum magnetic field strength that can be applied.
Factsheet 19.
We are now in a position to use Newton’s second law on the ions in the cyclotron that are moving in a circle:
F = ma where : m = mass of ion (kg)
Substituting into this equation the expressions for centripetal force and acceleration that are stated above we get:
mv2
Bqv = r
Rearranging this to make speed, v, the subject of the equation:
![]() Bqr v = m
Bqr v = m
For any particular ion, its charge, q, and its mass, m, will remain constant. This equation also shows that if the magnetic field strength is constant, the speed of the particle is proportional to the radius of its circular path. As the ions move from dee to dee, their speed increases. This means that the ions move in larger and larger circles as they accelerate up to the radius of the dees themselves, at which point they cannot be accelerated anymore and they are released towards the target.
|
Typical Exam Question (a) Calculate the energy gained by a proton in a cyclotron when itmoves between the two dees if the voltage between the dees is 4.0 kV. State your answer in joules. (The charge on a proton is 1.6 × 10-19C). [2] (b) Calculate the speed of the proton after it made 500 complete cycles.Assume the mass of the proton stays constant at 1.7 × 10-27kg. [4] (c) Calculate the radius of the circular path that this proton travelsaround if the magnetic field strength used is 0.50T. [3] (d) How long will it take a proton to complete one semicircular pathinside a dee? [3] (e) What frequency of alternating voltage should be used? [2] Answer (a) The proton will gain energy equal to the electrical potential energy thatit has at the start of its transfer between the two dees. Note that the question quotes kilovolts, kV, which must be converted into volts, V, before substituting into the equation. Energy gained = charge × voltage = qV = (1.6 × 10-19)(4000) = 6.4 × 10-16J (b) The energy gained by the proton will simply be 1000 times( 500 × two crossings per cycle) the energy calculated in part (a). We then have to equate all of this gain in energy to an increase in the kinetic energy of the proton. Gain in kinetic energy = (1000)(6.4 × 10-16) = 6.4 × 10-13J Therefore, ½mv2 = 6.4 × 10-13 v2 = (2)(6.4 × 10-27-13) = 7.53 × 1014
|
(c) Knowing values of charge and mass for the proton, and havingcalculated a value for speed, we can substitute these numbers into the equation derived earlier for the speed of ions in a cyclotron. The equation has to be rearranged to make radius, r, the subject of the equation, mv (1.7 × 10-27)(2.7 × 107) r = = -19 = 0.58 m Bq (0.5)(1.6 × 10 ) (d) We can use the simple equation: speed = distance/time with time as thesubject of the equation. We have a value for speed from part (b) and the distance travelled will be half a circumference of a circle with the radius calculated in part (c).
time taken = = speed (2.7 (e) The periodic time for one complete revolution made by the particle = (2)(6.7 × 10-8) = 1.34 × 10-7 s 1 1
periodic time 1.34 × 10
|
The above equation also shows that a larger magnetic field will create a larger speed for the particles. In large cyclotrons, very powerful superconducting magnets are often used instead of electromagnets.
As particles approach very high
speeds, close to the speed of light, their mass increases. This effect is
predicted by special relativity. This means that the particles spend slightly
longer in each dee. This means that the alternating voltage reverses too soon
for the particles to be accelerated across the gap. The synchronisation of the
voltage and the ions is lost. This happens at energies of about 20 MeV,
meaning that a more sophisticated particle accelerator is needed for higher
energies.
In a synchrotron, the radius of the circular path that the particles follow is kept constant. Hence the particles travel around an evacuated chamber that is shaped into a ring. A synchrotron consists of:
• An evacuated chamber shaped into a ring.
• A source of fast moving ions, usually from a ‘pre-accelerator’ such as a linear accelerator or a smaller circular accelerator.
• Magnets around the ring that can have a varying magnetic field strength. • Accelerating cavities around the ring that increase the speed of the particles.
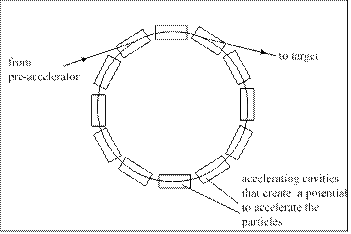
• The particles are kept moving in a circular path by magnets around the evacuated ring as shown in Fig 3.
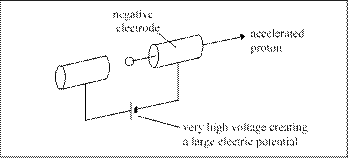 |
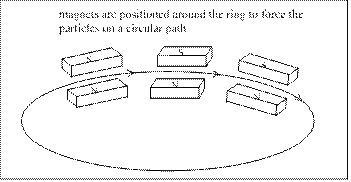
• The magnetic field strength of the magnets can be varied to make sure that the ions follow the same circular path regardless of their speed and their changing mass at higher energies.
• An electric potential is used to accelerate the particles in the accelerating cavities around the loop. Positive particles are accelerated towards a negative electrode inside the accelerating cavities as shown in Fig 4 below.
Because the magnets are around the ring, the centre of the magnet that has to be used in the cyclotron is not needed. This means that the radius of the circular path that the particles follow can be made much bigger (For example the largest synchrotron accelerator at CERN in Geneva has a circumference of 27km !)
|
The radius of the circular path of the particles must remain constant as they speed up and their mass increases at very high energies. This means that the size of the magnetic field must be varied and synchronised with the speed and mass of the particles. |
When charged particles move in a circular path, they lose kinetic energy. This energy is lost as electromagnetic radiation called ‘synchrotron radiation’. The loss of kinetic energy causes the particles to slow down unless they receive a boost of energy from the synchrotron. Therefore, just to keep the charged particles in a synchrotron moving at constant speed requires them to receive energy from the accelerator. This also means that a synchrotron can act as a source of electromagnetic radiation.
|
Charged particles moving in a circular path lose kinetic energy as electromagnetic radiation or synchrotron radiation. This would cause the particles to slow down and spiral into the centre of the accelerator unless they received constant boosts of energy from the accelerator. |
|
|
Typical Exam Question In a synchrotron, charged particles are kept moving in a circular path by magnets as they are accelerated to high energies. (a) Give two reasons why it is necessary to increase the strengthof the magnets as energy of the particles increases. (2) (b) The particles radiate electromagnetic radiation, or synchrotronradiation as they move in a their circular path. (i) Why do the particles need a constant boost of energy just tomaintain their speed? (2) (ii) How might this limit the energy that a charged particle can reach in any particular accelerator? (2) Answer (a) A stronger magnetic field is needed to change the direction of fastermoving particles. The mass of the particles increases and a stronger magnetic field is needed to change the direction of more massive particles. (b) (i) The particles lose kinetic energy as they emit electromagneticradiation. This kinetic energy is replaced, and the particle speed maintained, by a boost of energy from the accelerator (ii) Faster particles emit more energy as radiation when moving in a circle. More energy must be received from the accelerator to maintain speed. An accelerator can only provide a finite amount of energy to the particles. |
||
|
Exam Workshop This is a typical poor student’s answer to an exam question. The comments explain what is wrong with the answers and how they can be improved. The examiner’s answer is given below. The diagram below represents a cyclotron that is used to accelerate protons. The protons enter the accelerator at the centre and spiral outwards.
alternating p.d (a) Why do the protons accelerate moving from one half of thecyclotron into the opposite half? [2] The protons are attracted to the opposite dee. 1/2
(b) The largest radius of the circular path that the protons can followis equal to the radius of the cyclotron. Show that the maximum speed of a proton is equal to BqR/m. B is the magnetic field strength, q is the charge on a proton, R is the radius of the cyclotron and m is the mass of the proton. [3] mv2 Bqv = r
= m
|
(c) Calculate the maximum speed of a proton in a cyclotron ofdiameter 0.80m when the magnetic field strength is 0.60T. The charge on a proton is 1.6 × 10-19C and the mass is 1.7 × 10-27 kg.[2]
= = = 4.5 (1.7 × 10 )
(d) (i) State a difference in the path followed by a charged particle being accelerated by a synchrotron compared to the path shown above in a cyclotron. [1] The path in a synchrotron is circular 1/1 |
||||
|
( ( (c) ( |
Although this statement would probably get the mark it would have been better to make reference to the constant radius of the circle. |
||||
|
(ii) What difference in the design of the synchrotron makes this path possible? [1] The magnets 0/1 |
|||||
|
This answer is not specific enough. The student should state what it is about the magnetic field that is responsible for the circular path. |
|||||
|
Examiner’s Answers a) The opposite dee always has a negative potential. ✓ ✓ The negative potential attracts the proton, increasing its speed. b) Centripetal Force = mass × acceleration (in a circle) Bqv = mv2/r ⇒ v = Bqr/m ✓ ✓ When the speed is at a maximum, the radius of the circle = R Maximum v = BqR/m ✓
(1.7 (i) In a synchrotron, the particles follow a complete circular path ofconstant radius instead of two semi-circular paths of different radius as in a cyclotron.✓ (ii) The strength of the magnetic field can be varied.✓ |
|||||
(1) How does the speed of the particles being accelerated by a cyclotron change; (i) inside a dee and (ii) moving from one dee to the other?
(2) What keeps the particles moving in a circular path?
(3) What two factors limit the maximum speed that the particles can attain in a cyclotron?
(4) What are the limitations of a cyclotron and how does the synchrotron overcome these limitations?
(5) Why do charged particles moving in a circle lose kinetic energy?
(6) How is the energy of charged particles moving inside the circular tunnel of a synchrotron maintained?
1. (a) Calculate the energy given to a proton when it moves between 2 dees
that have a potential of 1500V across them. The charge on a proton
is 1.6 × 10-19C. [2]
(b) What would be the increase in speed of the proton of mass 1.7 ×10-27kg?
[3]
2. (a) Calculate the radius of the circular path followed by an electron travelling at a speed of 2.0 × 107 m/s when it is in a magnetic field of 0.10T, perpendicular to it motion. The charge on an electron is
1.6 × 10-19C and the mass of an electron is 9.11 × 10-31kg. [2]
(b) How long would it take this electron to travel one semi circle?[3]
Qualitative Test Answers
Answers can be found in the text
1. (a) Energy = qV = (1.6 × 10-19)(1500) = 2.4 × 10-16J
(b) Kinetic Energy = Energy gained
½mv2 = 2.4 × 10-16
2 2 × (2.4 × 10-16)
v =
1.7 × 10-27
= 2.8 × 1011
![]() v = √(2.8 x 1011) = 5.3 x 105 m/s
v = √(2.8 x 1011) = 5.3 x 105 m/s
2.
![]() (a) mv
(9.11 ×
10-31)(2
× 107) r = = -19
(a) mv
(9.11 ×
10-31)(2
× 107) r = = -19
Bq 0.1 × (1.6 × 10 )
= 1.1 × 10-3 m = 1.1mm
(b) distance speed =
time
distance (½ × circumference)
time = =
speed speed
 (½)(2π×)(1.1
107 )× 10-3) × 10-10 s
(½)(2π×)(1.1
107 )× 10-3) × 10-10 s
= = 1.8
(2
Physics Factsheets may be copied free of charge by teaching staff or students, provided that their school is a registered subscriber.
No part of these Factsheets may be reproduced, stored in a retrieval system, or transmitted, in any other form or by any other means, without the prior permission of the publisher. ISSN 1351-5136
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.