Действия с суммами нескольких слагаемых 2

6 класс

Тема.  Действия с суммами нескольких слагаемых.

Цель.   Продолжить формирование навыки применения распределительного закона при раскрытии скобок и  для вынесения общего множителя за скобки. раскрытия скобок, перед которыми стоит знак «+» или «–», заключения слагаемые в скобки, перед которыми поставим знак «+» или «–», действия с суммами нескольких слагаемых.

Ход урока.

I.    Организационный момент.

II.   Проверка домашнего задания.

III.      Актуализация опорных знаний.

1.  Как использовать распределительный закон для раскрытия скобок?

2.  Как использовать распределительный закон для вынесения общего множителя за скобки?

3.  Как раскрыть скобки, перед которыми стоит знак «+»? А вынести «+» за скобки?

4.  Как раскрыть скобки, перед которыми стоит знак «–»? А вынести «–» за скобки?

5.  Как сложить два отрицательных числа? А с разными знаками?

6.  Как вычесть два числа?

7.  Как умножить два отрицательных числа? А с разными знаками?

8.  Как разделить два отрицательных числа? А с разными знаками?

IV.       Самостоятельная работа.

1. Упростите числовое выражение:

1) ;

2) .

2. Вычислите наиболее простым способом:

1) ;

2) .

3. Найдите значение выражения:

.

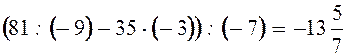1) ;              3) ;

2) ;           4) .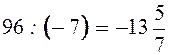

4. Вычислите:

1) (–76 + 125 – 37) – 125 + 37 = –76 + 125 – 37 – 125 + 37 = – 76;

2) – (– 79 – 39 + 81) + 81 – 39 = 79 + 39 – 81 + 81 – 39 = 79.

5. Вычислите:

1) (234 – 26) – 74 = 234 – 26 – 74 = 234 – 100 = 134;

2) – (541 – 39) + 61 = –541 + 39 + 61 = –541 + 100 = – 441.

V.  Объяснение нового материала.

Действия с суммами нескольких слагаемых.

Мы с вами уже знаем как раскрыть скобки, перед которыми стоит знак «+» или «–». Но встречаются суммы, в которых стоящие перед скобками знаки «+» и «–» обозначают действия сложения и вычитания. Как поступить в этом случае?

1) а + (b – с) = ?.    

Наводящие вопросы:

1)    Сколько слагаемых в примере?

2)    Какой знак стоит перед вторым слагаемым?

3)    А как раскрыть скобки, перед которыми стоит знак «+»?

Т.е в данном примере применимо изученное правило раскрытия скобок, перед которыми стоит знак «+». Значит:

а + (b – с) = а + b – с.

Пример 1. Раскройте скобки:

1)                                                                                                         7 + (8 – 3) = 7 + 8 – 3;   3) 6 + (– 7 – 10) = 6 – 7 – 10.

2)   –9 + (– 4 + 5) = –9 – 4 + 5;

2) а – (b – с) = ?.     

Наводящие вопросы:

1)    Сколько слагаемых в примере?

2)    Какой знак стоит перед вторым слагаемым?

3)    А как раскрыть скобки, перед которыми стоит знак «–»?

Т.е в данном примере применимо изученное правило раскрытия скобок, перед которыми стоит знак «–». Значит:

а – (b – с) = а – b + с.

Пример 2. Раскройте скобки:

1)                                                                                                         –8 – (5 – 9) = –8 – 5 + 9; 3) –7 – (– 8 – 4) = –7 + 8 + 4

2)   3 – (– 7 + 11) = 3 + 7 – 11;

При вычислении суммы нескольких слагаемых используют правила раскрытия скобок, заключения в скобки и законы сложения. Иногда складывают сначала положительные, потом отрицательные слагаемые и находят сумму полученных результатов, применяя правило сложения чисел с разными знаками.

VI.       Решение упражнений.

Уч.с.73 № 380(2ст.). Раскройте скобки и вычислите:

б) –49 – (–49 + 2) = –49 + 49 – 2 = – 2;

г) 100 – (–5 + 100) = 100 + 5 – 100 = 5;

е) (–78 + 23) + (27 + 78) = –78 + 23 + 27 + 78 = 50;

з) (105 – 48) – (62 + 105) = 105 – 48 – 62 – 105 = – 110.

Уч.с.74 № 381(1ст.). Вычислите, раскрывая скобки только в тех случаях, когда это облегчает вычисления:

а) 79 – (63 + 7) = 79 – 70 = 9;

г) 43 + (77 – 43) = 43 + 77 – 43 = 77;

ж) 93 – (68 + 93) = 93 – 68 – 93 = –68;

к) 48 – (18 + 19) = 48 – 18 – 19 = 30 – 19 = 11;

н) 52 – (32 – 41) = 52 – 32 + 41 = 20 + 41 = 61.

Уч.с.70 № 361(в). Вычислите:

в)

.

Подведение итогов урока. Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок.

Организуют обсуждение:

·         Какова была тема урока?

·         Какую задачу ставили?

·         Каким способом решали поставленную задачу?

·         Какие у вас были затруднения на уроке?

·         Нашли ли вы выход из затруднения?

·         Остались ли у вас затруднения после окончания урока?

·         Над чем необходимо продолжить работу?

VII.    Домашнее задание. § 2.11 (выучить теорию). № 379(1ст.), 380(1ст.), 381(3ст.).

1. Упростите числовое выражение:

1) ;                      2) .

2. Вычислите наиболее простым способом:

1) ;                         2) .

3. Вычислите:

1) (–76 + 125 – 37) – 125 + 37;       2) – (– 79 – 39 + 81) + 81 – 39.

4. Вычислите:

1) (234 – 26) – 74;                          2) – (541 – 39) + 61.

1. Упростите числовое выражение:

1) ;                      2) .

2. Вычислите наиболее простым способом:

1) ;                         2) .

3. Вычислите:

1) (–76 + 125 – 37) – 125 + 37;       2) – (– 79 – 39 + 81) + 81 – 39.

4. Вычислите:

1) (234 – 26) – 74;                          2) – (541 – 39) + 61.

1. Упростите числовое выражение:

1) ;                      2) .

2. Вычислите наиболее простым способом:

1) ;                         2) .

3. Вычислите:

1) (–76 + 125 – 37) – 125 + 37;       2) – (– 79 – 39 + 81) + 81 – 39.

4. Вычислите:

1) (234 – 26) – 74;                          2) – (541 – 39) + 61.

1. Упростите числовое выражение:

1) ;                      2) .

2. Вычислите наиболее простым способом:

1) ;                         2) .

3. Вычислите:

1) (–76 + 125 – 37) – 125 + 37;       2) – (– 79 – 39 + 81) + 81 – 39.

4. Вычислите:

1) (234 – 26) – 74;                          2) – (541 – 39) + 61.

1. Упростите числовое выражение:

1) ;                      2) .

2. Вычислите наиболее простым способом:

1) ;                         2) .

3. Найдите значение выражения:   .

4. Вычислите:

1) (–76 + 125 – 37) – 125 + 37;       2) – (– 79 – 39 + 81) + 81 – 39.

5. Вычислите:

1) (234 – 26) – 74;                          2) – (541 – 39) + 61.