Деление десятичных дробей

Тема.  Деление положительных десятичных дробей.

Дата: 12.03.20г.

Цель.   Проверить знания учащихся по теме «Умножения положительных десятичных дробей». Изучить правило деления десятичных дробей на натуральное число, правило деления на разрядную единицу 10; 100; 1000 и т.д.о. Сформировать навыки выполнения этих действий.

Ход урока.

I.    Организационный момент.

II.  Проверка домашнего задания.

III.      Актуализация опорных знаний.

1. Сформулируйте правило умножения десятичных дробей.

2. Сформулируйте правило умножения десятичных дробей на 10, 100, 1000 и т.д.

3. Сформулируйте правило умножения десятичных дробей на 0,1, 0,01, 0,001 и т.д.

4. Какие законы умножения знаете?

5. Как найти дробь от числа?

IV.       Повторение  по теме «Умножение положительных десятичных дробей».

V.   

1. Вычислите:

1) 54,56 × 10 = 545,6;          4) 54,56 × 0,1 = 5,456;

2) 37,57 × 100 = 3757;          5) 37,57  × 0,01 = 0,3757;

3) 89,19 × 1000 = 89190;      6) 89,19  × 0,001 = 0,08919.

.

VI.       Объяснение нового материала.

VII.    Деление на разрядную единицу 10; 100; 1000 и т.д.

1. Как умножить десятичную дробь на разрядную единицу 10, 100, 1000 и т.д?

2. По смыслу деления 36,7 : 10 = 3,67, поскольку 3,67 × 10 = 36,7

Проверь с помощью умножения следующие равенства:

1) 27,4 : 10 = 2,74;              3) 126,1 : 1000 = 0,126;

2) 3,47 : 100 = 0,0347;        4) 0,45 : 100 = 0,0045.

Сравни в каждом случае положение запятой в делимом и частном. Сопоставь это число с числом нулей в делителе.

3. Подумай, как можно сформулировать правило деления десятичной дроби на разрядную единицу 10, 100, 1000 и т.д.

Чтобы разделить десятичную дробь на разрядную единицу 10, 100, 1000 и т.д. надо в десятичной дроби перенести запятую  влево на столько знаков, сколько нулей содержит разрядная единица.

Пример 1. Чему равно частное:

1) 36,2 : 10 = 3,62;                       3) 216,7 : 1000 = 0,2167;

2) 8,54 : 100 = 0,0854;                 4) 0,13 : 100 = 0,0013.

Деление десятичных дробей на натуральное число.

Ø  Как называются компоненты при делении?

Ø  а : b = с. Что означает а : b? (найти с такое, что с × b = a)

      Как и в случае с натуральными числами, разделить десятичную дробь на натуральное число – означает найти такую дробь, при умножении которой на делитель получим делимое.

Пример 2. Вычислите:

1) 1,2 : 4 = 0,3, (Если целая часть делимого меньше делителя, то целая часть частного равна 0)поскольку 0,3 × 4 = 1,2;

2) 2,5 : 5 = 0,5 (Если целая часть делимого меньше делителя, то целая часть частного равна 0),

поскольку 0,5 × 5 = 2,5;

3) 1 : 2 = 0,5, (Если целая часть делимого меньше делителя, то целая часть частного равна 0), поскольку 0,5 × 2 = 1.

        В том случае, если деление не удается разделить устно, то выполняют деление «уголком». Письменное деление выполняется аналогично делению натуральных чисел.

Пример 3. Вычислите:

1) 32,2 : 14 = 2,3;

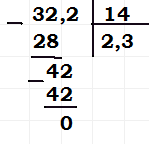Делим 32 целых на 14, в частном получаем 2 целых и  

ставим запятую, т.к. деление целой части закончено.

Остаток 4 единицы дробим в десятые и прибавляем (сносим) к ним 2 десятых, получаем 42 десятых.

Делим 42 на 14, в частном получаем 3 десятых и в остатке 0.

2) 1,781 : 13 = 0,137;         3) 7,843 : 341 = 0,023;         4) 3,1 : 5 = 0,62.

Если целая часть делимого меньше делителя, то целая часть частного равна 0.

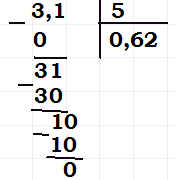
VIII.  Решение упражнений.

1. Чему равно частное:

1) 65,78 : 10 = 6,578;                   4) 12,43 : 100 = 0,1243;       

2) 87 : 10 = 8,7;                            5) 0,056 : 100 = 0,00056;    

3) 8 : 10 = 0,8;                              6) 54 : 1000 = 0,054.

2. Выполните деление:

1) 68,4 : 9 = 7,6;                           3) 27 : 5 = 5,4;

2) 39,6 : 15 = 2,64;                       4) 0,1547 : 17 = 0,0091.

IX.       Подведение итогов урока.

1. Как найти дробь от числа?

2. Сформулируйте правило умножения десятичных дробей на 10, 100, 1000 и т.д.

3. Сформулируйте правило умножения десятичных дробей на 0,1, 0,01, 0,001 и т.д.

4. Как разделить десятичную дробь на натуральное число?

X.  Домашнее задание. п. 4.6 (выучить теорию). № 818, 820, 821, 832.