Диаграммы Эйлера-Венна. Упрощение логических выражений

15-16 урок, 10 класс – практика

Учитель: Брух Т.В.

Дата:___________

Тема урока: «Диаграммы Эйлера-Венна.  Упрощение логических выражений».

Цель урока:

познакомить учащихся с решением логических задач средствами алгебры логики.

Задачи урока:

·       учить обучающихся решать логические задачи средствами алгебры логики;

·       способствовать формированию логического мышления, интереса к изучаемому материалу.

I.         Образовательные:

-         демонстрация учащимися знаний о методе решения логических задач средствами алгебры логики;

-         развитие навыков использования метода решения логических задач средствами алгебры логики при решении логических задач.

II. Развивающие:

-         развитие логического и критического мышления, способности четко формулировать свои мысли, выделять главное, существенное, рефлексировать;

-         формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в образовательной деятельности;

-         воспитание личной ответственности и ответственности перед другими обучающимся;

-         готовность и способность обучающихся к саморазвитию и личностному самоопределению.

III. Воспитательные:

-  Воспитывать у учащихся активность и стремление познавать новое;

-  Воспитывать аккуратность выполнения работы, трудолюбие, упорства достижения цели.

Ход урока.

1.Организационный момент.

Проверка готовности обучающихся к уроку. Приветствие.

2. Актуализация знаний. Проверка домашнего задания

2 задачи

Импликация, эквивалентность, предикаты (10-2 класс)

Задача 1. Петя, Вася и Маша остались дома одни. Кто-то из них ел варенье. На вопрос мамы, кто это сделал, они сказали:
а) Петя: "Я не ел. Маша тоже не ела."
б) Вася: "Маша действительно не ела. Это сделал Петя"
в) Маша: "Вася врет. Это он съел."

Выясните, кто ел варенье, если известно, что двое из них оба раза сказали правду, а третий один раз соврал, а один раз сказал правду.

Ответ. Варенье ел Вася, так как только при одном (третьем) варианте возможных значений ответ двоих - 1 и 1, а ответ одного - 0 и 1

Оказалось, что каждый из учеников был прав только в одном из двух своих утверждений.

Определите, кто из ребят, в каком задании допустил ошибку.

Задача 2. Митя, Сережа, Толя, Костя и Юра пришли в музей до открытия и встали в очередь в кассу. Митя пришел позже Сережи, Толя раньше Кости, Митя раньше Толи, Юра позже Кости. В каком порядке ребята стояли в очереди?

Задача 3. Четыре подруги — Маша, Полина, Ольга и Наташа – участвовали в соревнованиях по бегу и заняли первые четыре места. Установите, кто какое место занял, если известно, что в каждом из приведенных ниже ответов, которые дали девушки на вопрос опоздавшего к финишу корреспондента, кто какое место занял, верной является лишь половина ответа.

Наташа: “Ольга была второй, а Полина — первой”.

Маша: “Нет, Наташа. Ольга была первой, а второй была ты”.

Ольга: “Да что вы, девочки! Третьей была Маша, а Полина — четвертой”.

Задача 4. 

В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.

Один считает, что первой будет Наташа, а Маша будет второй.

Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место.

Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.

Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.

Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?

3.  Первичное усвоение новых знаний

Тема нашего урока: «Решение логических задач, используя диаграммы Эйлера-Венна». Открываем тетради, записываем число:

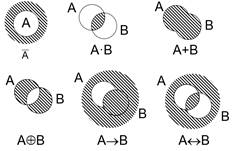
Множество – набор взаимосвязанных по какому-либо признаку или группе признаков объектов, которые можно рассматривать как единое целое.

Элементом множества называется каждый объект во множестве.

Пустое множество – множество не содержащее элементов (Æ).

Два множества А и В называются равными тогда и  только тогда, когда

Р_А(х)º Р_В(х).

Дополнением  ко множеству А относительно универсального множества I называется множество А, определяемое следующим

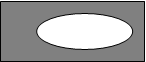Р_А(х)º Р_А(х)

Объединением множеств А и В называется множество, обозначаемое АÈВ, определяемое следующим

Р_АÈВ(х)ºР_A(х)ÚР_В(х)

Пересечением множеств А и В называется множество, обозначаемое АÇВ, определяемое следующим
 Р_АÇВ(х)ºР_A(х)× Р_В(х)

Разностью множеств А и В называется множество, обозначаемое А\В определяемое следующим

Р_А\В(х)ºР_A(х)× Р_В(х)

Симметрической разностью множеств А и В называется множество, обозначаемое АDВ определяемое следующим

АDВ=(А\В) È(В\А)

Множество А является подмножеством множества В (AÌB) тогда и только тогда, когда каждый элемент множества А является элементом множества В, т.е.

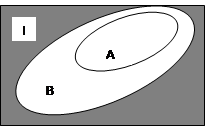AÌBÛР_А(х) ® Р_В(х)º1.

4.  Первичное закрепление

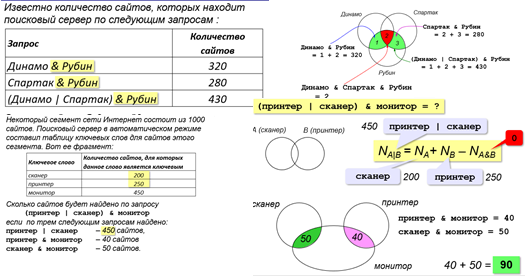
Исходя из условия задачи, сколько диаграмм Эйлера-Венна у нас дано? (три)

5. Информация о домашнем задании, инструктаж по его выполнению

Домашнее задание.

1. Три подружки — Оля, Маша и Юля — купили в магазине груши, яблоки и сливы, причем каждая девочка покупала только один вид фруктов и все покупки у них были разные. На вопрос, кто что купил, продавец ответил: “Оля купила груши. Маша точно не груши. Юля — не сливы”. Как оказалось позже, два из трех ответов были ложными и только один истинным. Кто что купил?

2. Учитель проводил диктант по теме “Определения”. Каждый, из учеников – Коля, Сережа, Ваня, Толя, Надя — ошибся в одном из пяти заданий диктанта, причем все они ошиблись в разных заданиях. По окончании работы учащиеся высказались об ошибках, сделанных их одноклассниками, следующим образом.

1-й ученик: “Коля ошибся в первом задании, а Ваня – в четвертом”.

2-й ученик: “Сережа ошибся во втором, а Ваня — в четвертом задании”.

3-й ученик: “Сережа ошибся во втором, а Коля – в третьем задании”.

4-й ученик: “Толя ошибся в первом задании, а Надя – во втором”.

5-й ученик: “Надя ошиблась в третьем задании, а Толя – в пятом”.

Оказалось, что каждый из учеников был прав только в одном из двух своих утверждений. Определите, кто из ребят, в каком задании допустил ошибку.

3.

Скачано с www.znanio.ru