Муниципальное бюджетное общеобразовательное учреждение города Ульяновска

«Средняя школа № 29»

 

 

 

 

 

 

 

 

Дополнительная общеобразовательная общеразвивающая краткосрочная программа естественно-научной направленности

 «Занимательная математика»

 

 

 

Возраст обучающихся – 12-14 лет

стартовый уровень

Срок реализации – 1 год (144 часа):

2 модуля: 1 модуль - 64 часов, 2 модуль - 80

 

 

 

Программа разработана:

Леухиной Викторией Игоревной,

педагогом дополнительного образования

 

 

 

 

 

г. Ульяновск, 2020

СОДЕРЖАНИЕ

1.    Комплекс основных характеристик дополнительной общеобразовательной общеразвивающей программы.. 3

1.1 Пояснительная записка программы.. 3

1.2 Цели и задачи программы.. 5

1.3 Содержание программы.. 6

1.4 Планируемые результаты.. 13

2.    Комплекс организационно-педагогических условий. 15

2.1 Календарный учебный график. 15

2.2 Условия реализации программы.. 23

2.3 Формы аттестации.. 23

2.4 Оценочные материалы.. 24

2.6.Список литературы.. 25

2.7.Соответствие программы нормативным документам.. 26

Приложение 1. 27

Приложение 2. 27

Приложение 3. 29

Приложение 4. 32

Приложение 5. 34

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.    Комплекс основных характеристик дополнительной общеобразовательной общеразвивающей программы

 

1.1 Пояснительная записка программы

Дополнительная       общеобразовательная           общеразвивающая программа «Занимательная математика» составлена на основе Федеральным законом «Об образовании в Российской Федерации» № 273-ФЗ от 29.12.2012 г.

Данная программа позволит учащимся расширить свои возможности и навыки в изучении математики, что положительно отразится на их успеваемости.

Особенность построения курса состоит в том, что он ориентирует педагога на деятельностный подход в обучении, на организацию разнообразной развивающей деятельности, отвечающей современным психолого- педагогическим воззрениям, на использование современных технологий.

В ходе освоения содержания курса математики в 6 классах учащиеся получают возможность развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру.

При изучении математики основное внимание уделяется формированию широкого круга практических навыков вычислений (прочные навыки выполнения действий над сравнительно небольшими числами, приёмы прикидки и оценки результатов действий, проверка результата на правдоподобие и др.).

Большое внимание уделяется накоплению учащимися опыта геометрической деятельности, развитию их пространственных представлений, глазомера, наблюдательности. Геометрические понятия возникают в естественном контексте из практической деятельности и ассоциируются со зрительным образом. Их рассмотрение не предполагает формализации, однако способствует накоплению достаточно большого объёма геометрических знаний и развитию геометрического мышления. Значительное место занимают упражнения, в которых требуется начертить, перерисовать, измерить, найти на рисунке или предмете, вырезать, разрезать, составить фигуру и др.

Программа дополнительного образования «Занимательная математика» реализуется в рамках естественно-научной направленности МБОУ СШ №29 г. Ульяновска, так как формирует представления об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.

По отношению к программам общего образования данная программа является дополнительной.

Уровень освоения программы: стартовый.

Актуальность программы «Занимательная математика» обусловлена тем, что всегда математика, занимает важное место в жизни каждого человека. Она позволит подготовить учащихся к профильному обучению на старшем этапе.

Важное место на занятиях по программе дополнительного образования «Занимательная математика»  занимает решение математических           ребусов, логических задач, кроссвордов, загадок, участие в викторинах, турнирах, применение кейс-технологий, что обеспечивает устойчивое внимание к изучаемому материалу. «Серьёзная математика» на занятиях с использованием игровых форм обучения становится интересной, понятной.

Новизна программы.

В образовательном процессе используется современные технологии и методики, предлагающие системно-деятельный подход к формированию предметных, метапредметных и личностных качеств учащихся. Программа «Занимательная математика» даёт возможность познать и расширить знания по изучаемым предметам. Новизна в программе от существующей в том, что формируются метапредметные навыки, игровая деятельность и кейс-технологии в расширении понимания и изучения математики.

Отличительные особенности программы заключаются в использовании кейс-технологий, игровой деятельности, направленные на расширение знаний и понимания математики.

Инновационность заключается в использовании специально подобранных методических материалов, технологий, методов и подходов к дистанционному обучению в современных условиях.

Адресат программы. Программа дополнительного образования «Занимательная математика» предназначена для детей среднего школьного возраста (12-14 лет).

Объём программы. Программа рассчитана на 144 часа обучения (36 недель 2 занятия в неделю по 2 академических часа). 1 модуль с 1 сентября по 31 декабря 68 часов, 2 модуль с 1 января по 31 мая 76 часов.

Формы обучения и виды занятий. Основной формой обучения является очная форма обучения; допускаются дистанционное, индивидуальное, в том числе ускоренное обучение, регламентируемые локальными актами муниципального бюджетного общеобразовательного учреждения г. Ульяновска «Средняя школа №29».

Виды занятий по программе: беседа, занятие-игра, викторины, кроссворды, кейс-технологии, практические занятия.

Формы и методы проведения занятий: групповая форма работы: объяснение, познавательная беседа, наблюдение, демонстрация иллюстраций, таблиц, решение задач, деятельность совместно с педагогом и самостоятельная работа учащихся.

Комплектование в группы свободное, по собеседованию.

Режим занятий – 2 раза в неделю по 2 академических часа.  В случае карантинных мер, при вынужденном переходе на дистанционное обучение академический час сокращается на основании Приложения 7. п.4.7 СанПин 2.2.2/2.4.1340-03 «Гигиенические требования к персональным электронно-вычислительным машинам и организации работы». Внеучебные занятия с использованием ПЭВМ рекомендуется проводить не чаще 2 раз в неделю общей продолжительностью: - для обучающихся во II-V классах не более 60 мин, для VI классов и старше - не более 90 мин» (при отсутствии информации о качестве используемых мониторов).

 

 

 

 

 

 

 

 

 

 

 

 

1.2   Цели и задачи программы

Цель: формирование и развитие интеллектуальной активности, поддержание устойчивого интереса к математике, развитие логического мышления и математической речи.

Задачи: 

Обучающие:

-     обучать основным приемам решения математических задач;

-     обобщать опыт применения алгоритмов арифметических действий для вычислений;

-     обучать правильному применению математической терминологии;

-     обучать делать выводы и обобщения, обосновывать собственные мысли;

-     повышать мотивацию и формировать устойчивый интерес к изучению математики;

-     обучать основам геометрических построений.

Развивающие:

-     развивать речь, применять терминологию для описания математических объектов и процессов окружающего мира в количественном и пространственном отношениях;

-     развивать потребность узнавать новое, проявлять интерес к занятиям математикой, стремиться использовать математические знания и умения в повседневной жизни;

-     развивать мышление: умение анализировать, обобщать, систематизировать знания и обогащать математический опыт.

Воспитательные:

-     воспитывать самостоятельность, уверенность в своих силах;

-     воспитывать ценностное отношение к знаниям, интерес к изучаемому предмету;

-     развивать коммуникативные навыки;

-     воспитывать трудолюбие, стремление добиваться поставленной цели.

 

 

 

 

 

 

 

 

 

1.3 Содержание программы

 

Программой предусмотрено формирование необходимых теоретических знаний и практических умений.

Теоретическая часть представлена в виде занятий, игр, демонстрацией наглядных пособи, обменом опыта и мнения, а также при помощи бесед и диспутов.

Практическая часть представлена в виде практического закрепления знаний, навыков, решения задач. Важным является развитие таких умений, как умение анализировать, сравнивать, применять знания в новой ситуации.

Образовательный процесс осуществляется на основе личностно-ориентированного подхода и основных дидактических принципов:

Принцип воспитания. Заключается в формировании у учащихся интереса к этому предмету, выработке у них стремления к новым знаниям, к их полному и прочному усвоению, формировании умения пользоваться полученными знаниями и расширять их за счет самостоятельного изучения.

Принцип наглядности. Вытекает из сущности процесса восприятия, осмысления и обобщения учащимися изучаемого материала. Он означает, что в обучении необходимо, следуя логике процесса усвоения знаний, на каждом этапе обучения найти его исходное начало в фактах и наблюдениях единичного или в аксиомах, научных понятиях и теориях, после чего определить закономерный переход от восприятия единичного, конкретного предмета к общему, абстрактному или, наоборот, от общего, абстрактного к единичному, конкретному.

Принцип сознательности, активности и самостоятельности. Заключается в целенаправленном активном восприятии изучаемых явлений, их осмыслении, творческой переработке и применении. Сознательность понимается в дидактике как овладение учащимися данными науки, учебным материалом, глубокое осмысление его, умение пользоваться знаниями на практике в новых условиях, превращение знаний в убеждение, в руководство к действию.

Познавательная активность есть деятельное состояние учащегося, которое характеризуется стремлением к учению, умственным напряжением и проявлением волевых усилий в процессе овладения знаниями.

Познавательная самостоятельность является высшей формой активности и сознательности учащихся в процессе учения. Поэтому осуществление в обучении сознательного и активного процесса учения формирует такое качество личности, как познавательная самостоятельность.

Принцип прочного усвоения учащимися знаний, умений и навыков. Заключается в том, что опираться на приобретенные знания, умения и навыки на последующих этапах обучения и пользоваться ими в жизни можно лишь тогда, когда они усвоены твердо, длительное время удерживаются в памяти. В процессе обучения, учащиеся не только приобретают знания, умения и навыки, но и закрепляют и совершенствуют их.

Принцип систематичности и последовательности в обучении.

Систематичность в обучении математике предполагает соблюдение определенного порядка в рассмотрении и изучении фактов и постепенное овладение основными понятиями и положениями школьного курса математики.

Последовательность в обучении математике означает, что обучение идет от простого к сложному, от представлений к понятиям, от известного к неизвестному, от знания к умению, а от него – к навыку.

Принцип дифференцированного (индивидуального) подхода к учащимся. Обусловливается особенностями индивидуального развития детей, типов высшей нервной деятельности, а также стремлением наилучшим образом развивать творческие силы и способности учащихся.

Этот принцип предполагает оптимальное приспособление учебного материала и методов обучения к индивидуальным способностям каждого школьника. Основным средством реализации принципа индивидуального подхода являются индивидуальные самостоятельные работы, предназначенные для учащихся.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Учебный план

№	Блок / Наименование темы	Количество часов			Формы аттестации/ контроля
		всего	теория	практика
	МОДУЛЬ 1
	Раздел 1. Математика – это интересно.	32	13	23
1.1	Вводное занятие. Введение в программу. Правила ТБ, ПДД. Тема 1.1.  Введение. Инструктаж по Т.Б. Теория. Цели и задачи, стоящие перед группой в процессе обучения, виды деятельности, предусмотренные программой, правила поведения на занятиях и техника безопасности. Знакомство с основными разделами математики. Практика. Рассказ, беседа, инструктаж по технике безопасности, анкетирование. Ознакомление детей с разделами программы, планом занятий. Обсуждение правил поведения в кабинете. Беседа о правилах, принятых на занятиях объединения. Диагностическое обследование с целью выявления индивидуального маршрута. Решение занимательных задач.	2	1	1	Беседа, опрос, решение задач.
1.2	Тема 1.2. Из истории математики. Теория. Математика древних народов (Древний Восток: Египет, Вавилон, Китай; Древняя Греция; Индия, страны Ислама). Западная Европа. Математика народов нашей Родины. Практика. Учить организовывать последовательность работы. Создание творческого проекта.	8	2	6	Тестирование.
1.3	Тема 1.3. Занимательная арифметика. Теория. Запись цифр и чисел у других народов. Как люди научились считать. Старинные системы записи чисел. Цифры у разных народов. Римская и арабская нумерация. Системы счисления. Открытие нуля. Мы живём в мире больших чисел. Числа великаны. Названия больших чисел. Числа – малютки. Решение задач с большими и малыми числами. Упражнения на быстрый счёт. Некоторые приёмы быстрого счёта. Возведение в квадрат двузначных чисел. Практика. Решение задач на быстрый счет. Упражнения на быстрый счет в уме. Интересные приемы устного счета. Возведение в квадрат двузначных чисел.	22	10	16	Творческая работа (проект).
	Раздел 2. Решение задач	32	9	19
2.1	Тема 2.1. Признаки делимости. Решение задач. Теория. Таблица признаков делимости чисел. Признаки делимости на 2, 4,6, 8. Признаки делимости на 13 и 19. Признаки делимости на 7 и 11. Признаки делимости по последним цифрам. Признаки делимости по сумме цифр. Практика. Решение задач с использованием признаков делимости чисел.	10	4	6	Беседа. Тестирование.
2.2	Тема 2.1. Занимательные задачи. Теория. Классификация занимательных задач. Задачи на переливания, на взвешивание, на переправы, на расстановку скобок и знаков, на перекладывание спичек. Числовые ребусы. Расшифровка ребусов. Текстовые задачи (математические игры, выигрышные ситуации). Математические софизмы. Логические задачи.   Практика. Решение задач на переливания, на взвешивание, на переправы, на расстановку скобок и знаков, на перекладывание спичек. Числовые ребусы. Расшифровка ребусов. Решение текстовых задач (математические игры, выигрышные ситуации). Математические софизмы. Логические задачи.	18	5	13	Математическая игра.
	Итого модуль 1:	64	22	42
	МОДУЛЬ 2
	Раздел 3. Комбинаторика и теория графов. Нестандартные задачи	34	10	24
3.1	Тема 3.1. Принцип Дирихле. Решение задач на принцип Дирихле. Теория. Понятие комбинаторики. Принцип Дирихле.  Практика. Решение задач на принцип Дирихле.	8	2	6	Беседа. Текущий контроль.
3.2	Тема 3.2. Понятие графа. Решение задач Теория. Понятие графа. Степени вершин и подсчет числа ребер. Применение графов к решению задач. Деревья. Применение графов к решению задач. Формула Эйлера. Практика. Решение задач. Деревья. Решение задач с помощью формулы Эйлера.	8	2	6	Устная оценка. Текущий контроль.
3.3	Тема 3.3. Нестандартные задачи. Теория. Нестандартные задачи. Восстановление знаков действий. Восстановление цифр натуральных чисел. Задачи на четные и нечетные числа. Задачи на простые и составные числа. Старинные задачи. Задачи-шутки. Задачи на составление уравнений. Задачи на логику. Задачи на проценты. Практика. Решение задач на восстановление знаков действий, восстановление цифр натуральных чисел.  Решение задач на четные и нечетные числа, на простые и составные числа. Старинные задачи, задачи – шутки, задачи на логику,  задачи на проценты.	18	6	12	Тестирование.
	Раздел 4. Загадочная и уникальная геометрия	30	6	24
	Тема 4.1. Геометрия на клетчатой бумаге. Задачи на разрезание Теория. Задачи на разрезание на клетчатой бумаге. Пентамино. Сотни фигур из 7 частей (танграм, полимино). Задачи на раскраску. Практика. Решение задач на разрезание на клетчатой бумаге, пентамино, на раскраску, танграм, полимино.	16	4	12	Опрос.
	Тема 4.2. Пространственные фигуры. Конструирование фигур Теория. Знакомство с пространственными фигурами. Конструирование фигур. Площади пространственных фигур. Объемы пространственных фигур. Геометрия в пространстве: задачи, связанные с прямоугольным параллелепипедом. Практика. Решение задач на площади пространственных фигур. Решение задач на объемы пространственных фигур. Геометрия в пространстве: задачи, связанные с прямоугольным параллелепипедом.	14	2	12	Творческая работа.
	Раздел 5. Мозговой штурм!	14	1	12
	Тема 5.1. Кроссворды и чайнворды Теория. История создания кроссворда. Правила классического кроссворда. Разновидности кроссвордов. Понятие линейного и трехмерного кроссворда. Практика. Творческая работа по составлению кроссвордов и чайнвордов.	7	1	6	Творческая работа.
	Тема 5.2. Математические викторины, игры, КВН, соревнования Теория. Математические викторины, игры, КВН. Практика. Проведение математических викторин, КВН, игр.	7	1	6	Беседа.
	Раздел 6. Подведение итогов.	2	1	1
	Теория. Подведение итогов работы объединения за   год.  Поощрение актива.       Практика. Математическая викторина.	2	1	1	Итоговая проверка.
	Итого модуль 2:	80	19	61
	Итого:	144	41	103

 

 

 

 

1.4    Планируемые результаты

Личностные результаты:

У учащихся будут сформированы:

1. Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

2. Умение контролировать процесс и результат учебной математической
деятельности;

У учащихся могут быть сформированы:

1. Критичность мышления, умение распознавать логически некорректные
высказывания, отличать гипотезу от факта;

2. Креативность мышления, инициатива, находчивость, активность при решении
задач.

Метапредметные результаты:

Регулятивные:

Учащиеся научатся:

1. Формулировать и удерживать учебную задачу;

2. Планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.

Учащиеся получат возможность научиться:

1. Предвидеть возможности получения конкретного результата при решении задач;

2. Прилагать волевые усилия и преодолевать трудности и препятствия на пути достижения целей.

Познавательные:

Учащиеся научатся:

1. Осуществлять выбор наиболее эффективных способов решения задач в
зависимости от конкретных условий;

2. Находить в различных источниках информацию и представлять ее в понятной форме;

3. Создавать и преобразовывать модели и схемы для решения задач.

Учащиеся получат возможность научиться:

1. Планировать и осуществлять деятельность, направленную на решение задачи исследовательского характера;

2. Выбирать наиболее рациональные и эффективные способы решения задач;

3. Выдвигать гипотезы при решении учебных и понимать необходимость их проверки.

Коммуникативные

Учащиеся научатся:

1. Организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками;

2. Взаимодействовать и находить общие способы работы, работать в группе, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов, слушать партнера, аргументировать и отстаивать свое мнение;

3. Аргументировать свою позицию и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности.

Учащиеся получат возможность научиться:

1. Продуктивно разрешать конфликты на основе учета интересов и позиций всех

участников, договариваться и приходить к общему решению в совместной деятельности;

2. Оказывать поддержку и содействие тем, от кого зависит достижение цели в совместной деятельности.

К концу изучаемого курса учащиеся должны знать/уметь:

Знать:

-     старинные системы записи чисел, записи цифр и чисел у других народов;

-     названия больших чисел;

-     свойства чисел натурального ряда, арифметические действия над натуральными числами и нулём и их свойства, понятие квадрата и куба числа;

-     приёмы быстрого счёта;

-     методы решения логических задач;

-     свойства простейших геометрических фигур на плоскости;

-     понятие графа;

-     площади пространственных фигур;

-     объемы пространственных фигур.

Уметь:

-     читать и записывать римские числа;

-     читать и записывать большие числа;

-     пользоваться приёмами быстрого счёта;

-     решать текстовые задачи на движение, на взвешивание, на переливание;

-     использовать различные приёмы при решении логических задач;

-     решать геометрические задачи на разрезание, задачи со спичками, геометрические головоломки, простейшие задачи на графы;

-     решать математические ребусы, кроссворды, чайнворды, софизмы, показывать математические фокусы;

-     выполнять проектные работы.

 

 

2.    Комплекс организационно-педагогических условий

 

 2.1 Календарный учебный график

Модуль 1:

№ п/п	Месяц	Число	Время проведения занятия	Форма занятия	Кол-во часов	Тема занятия	Место проведения	Форма контроля
1.				Введение новых знаний.	2	Вводное занятие. Введение в программу. Правила ТБ, ПДД.	СШ №29, каб. № 203	Беседа, опрос.
2.				Введение новых знаний. Комбинированное. Семинар.	2	Математика Древних народов («Древний Восток: Египет, Вавилон, Китай»).	СШ №29, каб. № 203	Творческий проект.
3.				Введение новых знаний. Комбинированное. Семинар.	2	Математика Древних народов («Древняя Греция, Индия. Страны Ислама».)	СШ №29, каб. № 203	Творческий проект.
4.				Введение новых знаний. Комбинированное. Семинар.	2	Западная Европа.	СШ №29, каб. № 203	Творческий проект..
5.				Введение новых знаний. Комбинированное. Семинар.	2	Математика народов нашей Родины.	СШ №29, каб. № 203	Творческий проект.
6.				Введение новых знаний. Комбинированное. Семинар.	2	«История арифметики. Счёт и числа».	СШ №29, каб. № 203	Творческий проект.
7.				Введение новых знаний. Комбинированное. Семинар.	2	«История развития чисел и счета. Системы счисления».	СШ №29, каб. № 203	Творческий проект.
8.				Введение новых знаний. Комбинированное. Семинар.	2	«История развития чисел и счета. Системы счисления».	СШ №29, каб. № 203	Творческий проект.
9.				Введение новых знаний. Комбинированное. Семинар.	2	«История развития чисел и счета. Системы счисления».	СШ №29, каб. № 203	Текущий контроль.
10.				Комбинированное. Семинар.	2	«Магические свойства чисел».	СШ №29, каб. № 203	Текущий контроль.
11.				Введение новых знаний. Комбинированное. Решение примеров.	2	«Приёмы устного счёта»	СШ №29, каб. № 203	Текущий контроль.
12.				Комбинированное. Решение примеров.	2	«Приёмы устного счёта»	СШ №29, каб. № 203	Опрос. Текущий контроль.
13.				Введение новых знаний. Комбинированное. Решение примеров.	2	«Нестандартные приёмы умножения»	СШ №29, каб. № 203	Текущий контроль.
14.				Комбинированное. Решение примеров.	2	«Нестандартные приёмы умножения»	СШ №29, каб. № 203	Тестирование.
15.				Введение новых знаний. Комбинированное. Решение примеров.	2	«Возведение в квадрат двузначных чисел».	СШ №29, каб. № 203	Текущий контроль.
16.				Комбинированное. Решение примеров.	2	«Возведение в квадрат двузначных чисел».	СШ №29, каб. № 203	Текущий контроль.
17.				Комбинированное. Решение примеров.	2	«Возведение в квадрат двузначных чисел».	СШ №29, каб. № 203	Текущий контроль.
18.				Комбинированное. Решение примеров.	2	«Возведение в квадрат двузначных чисел».	СШ №29, каб. № 203	Тестирование.
19.				Введение новых знаний. Комбинированное. Решение примеров.	2	Признаки делимости чисел.	СШ №29, каб. № 203	Текущий контроль.
20.				Введение новых знаний. Комбинированное. Решение примеров.	2	Признаки делимости чисел на 2, 4, 6, 8.	СШ №29, каб. № 203	Текущий контроль.
21.				Введение новых знаний. Комбинированное. Решение примеров.	2	Признаки делимости чисел на 13 и 19, 7 и 11.	СШ №29, каб. № 203	Текущий контроль.
22.				Введение новых знаний. Комбинированное. Решение примеров.	2	Признаки делимости чисел по последним цифрам.	СШ №29, каб. № 203	Опрос.
23.				Введение новых знаний. Комбинированное. Решение примеров.	2	Признаки делимости чисел по сумме чисел.	СШ №29, каб. № 203	Опрос. Тестирование.
24.				Введение новых знаний. Комбинированное. Решение задач.	2	Занимательные задачи.	СШ №29, каб. № 203	Текущий контроль.
25.				Комбинированное. Решение задач.	2	Решение задач на переливание.	СШ №29, каб. № 203	Текущий контроль.
26.				Комбинированное. Решение задач.	2	Решение задач на взвешивание.	СШ №29, каб. № 203	Текущий контроль.
27.				Комбинированное. Решение задач.	2	Решение задач на взвешивание.	СШ №29, каб. № 203	Опрос. Текущий контроль,
28.				Комбинированное. Решение задач.	2	Решение задач на движение.	СШ №29, каб. № 203	Текущий контроль.
29.				Комбинированное. Решение задач.	2	Задачи со спичками.	СШ №29, каб. № 203	Текущий контроль.
30.				Комбинированное. Решение ребусов.	2	Ребусы в жизни и быту.	СШ №29, каб. № 203	Текущий контроль.
31.				Комбинированное. Решение ребусов.	2	Числовые ребусы.	СШ №29, каб. № 203	Тесты, итоговый контроль.
32.				Комбинированное. Игра.	2	Игра «Мозговой штурм»	СШ №29, каб. № 203	Математическая игра.
				Итого модуль 1:	64

 

Модуль 2

№ п/п	Месяц	Число	Время проведения занятия	Форма занятия	Кол-во часов	Тема занятия	Место проведе-ния	Форма контроля
1.				Введение новых знаний. Комбинированное. Семинар.	2	Понятие комбинаторики.	СШ №29, каб. № 203	Текущий контроль.
2.				Введение новых знаний. Комбинированное. Семинар.	2	Принцип Дирихле.	СШ №29, каб. № 203	Опрос. Текущий контроль.
3.				Комбинированное. Решение задач.	2	Решение задач на принцип Дирихле.	СШ №29, каб. № 203	Текущий контроль.
4.				Комбинированное. Решение задач.	2	Решение задач на принцип Дирихле.	СШ №29, каб. № 203	Тестирование. Текущий контроль.
5.				Введение новых знаний. Комбинированное. Решение задач.	2	Знакомство с графами. Решение задач с помощью графа.	СШ №29, каб. № 203	Текущий контроль.
6.				Комбинированное. Решение задач.	2	Решение задач с помощью графа.	СШ №29, каб. № 203	Текущий контроль.
7.				Комбинированное. Решение задач.	2	Решение задач с помощью графа. Формула Эйлера.	СШ №29, каб. № 203	Текущий контроль, выставка
8.				Комбинированное. Решение задач.	2	Применение графов.	СШ №29, каб. № 203	Текущий контроль.
9.				Введение новых знаний. Комбинированное. Решение задач.	2	Нестандартные задачи.	СШ №29, каб. № 203	Текущий контроль.
10.				Комбинированное. Решение задач.	2	Решение нестандартных задач.	СШ №29, каб. № 203	Опрос. Текущий контроль, выставка
11.				Комбинированное. Решение задач.	2	Решение нестандартных задач.	СШ №29, каб. № 203	Текущий контроль.
12.				Введение новых знаний. Комбинированное. Решение задач.	2	Решение задач на чётные и нечётные, простые и составные числа.	СШ №29, каб. № 203	Текущий контроль, выставка
13.				Введение новых знаний. Комбинированное. Решение задач.	2	Решение задач на логику.	СШ №29, каб. № 203	Текущий контроль.
14.				Введение новых знаний. Комбинированное. Решение задач.	2	Решение задач с помощью уравнений.	СШ №29, каб. № 203	Текущий контроль, выставка
15.				Комбинированное. Решение задач.	2	Решение задач с помощью уравнений.	СШ №29, каб. № 203	Текущий контроль.
16.				Введение новых знаний. Комбинированное. Решение задач.	2	Решение задач на проценты.	СШ №29, каб. № 203	Опрос. Текущий контроль, выставка
17.				Комбинированное. Решение задач.	2	Решение задач на проценты.	СШ №29, каб. № 203	Текущий контроль.
18.				Комбинированное. Решение задач.	2	Решение задач на разрезание.	СШ №29, каб. № 203	Текущий контроль, выставка
19.				Комбинированное. Решение задач.	2	Решение задач на разрезание.	СШ №29, каб. № 203	Текущий контроль
20.				Комбинированное. Решение задач.	2	Решение задач на разрезание.	СШ №29, каб. № 203	Тесты, Текущий контроль, выставка
21.				Комбинированное. Игра.	2	Игра «Пентамино»	СШ №29, каб. № 203	Текущий контроль.
22.				Комбинированное. Решение задач.	2	Решение задач на разрезание	СШ №29, каб. № 203	Беседа. Текущий контроль, выставка
23.				Введение новых знаний. Комбинированное. Практическая работа.	2	Танграм своими руками.	СШ №29, каб. № 203	Текущий контроль.
24.				Комбинированное. Решение задач.	2	Решение задач на разрезание.	СШ №29, каб. № 203	Беседа. Текущий контроль, выставка
25.				Введение новых знаний. Комбинированное. Игра.	2	Логическая игра «Полимино».	СШ №29, каб. № 203	Текущий контроль.
26.				Введение новых знаний. Комбинированное. Решение задач.	2	Фигуры в пространстве. Конструирование фигур.	СШ №29, каб. № 203	Беседа. Текущий контроль, выставка
27.				Комбинированное. Решение задач.	2	Площади и объемы пространственных фигур.	СШ №29, каб. № 203	Текущий контроль.
28.				Комбинированное. Решение задач.	2	Решение задач на нахождение объема и площади поверхности  пространственных фигур.	СШ №29, каб. № 203	Текущий контроль. Выставка.
29.				Комбинированное. Решение задач.	2	Решение задач на нахождение объема и площади поверхности пространственных фигур.	СШ №29, каб. № 203	Текущий контроль.
30.				Комбинированное. Решение задач.	2	Решение задач на нахождение объема и площади поверхности пространственных фигур.	СШ №29, каб. № 203	Текущий контроль.
31.				Комбинированное. Решение задач.	2	Решение задач.	СШ №29, каб. № 203	Текущий контроль, выставка
32.				Комбинированное. Решение задач.	2	Решение задач.	СШ №29, каб. № 203	Текущий контроль.
33.				Комбинированное. Решение задач.	2	Решение задач.	СШ №29, каб. № 203	Текущий контроль.
34.				Введение новых знаний. Комбинированное. Семинар.	2	История появления кроссворда. Разновидности кроссвордов.	СШ №29, каб. № 203	Тесты. Текущий контроль. Выставка.
35.				Комбинированное. Практическая работа.	2	Создание математических кроссвордов, чайнвордов.	СШ №29, каб. № 203	Творческая работа.
36.				Комбинированное. Решение кроссвордов.	2	Решение математических кроссвордов, чайнвордов.	СШ №29, каб. № 203	Опрос. Текущий контроль.
37.				Комбинированное. Игра.	2	Математический КВН.	СШ №29, каб. № 203	Текущий контроль.
38.				Комбинированное. Игра.	2	Игра «Своя игра!»	СШ №29, каб. № 203	Текущий контроль.
39.				Комбинированное. Игра.	2	Игра «Математическое путешествие»	СШ №29, каб. № 203	Текущий контроль.
40.				Контрольное	2	Математическая викторина. Подведение итогов.	СШ №29, каб. № 203	Итоговая викторина.
				Итого модуль 2:	80
				Итого (модуль 1 + модуль 2):	144

 

 

 

2.2 Условия реализации программы

 

Для успешной реализации программы необходимо кадровое, материально-техническое, информационно-методическое обеспечение:

1.    Кадровое обеспечение.

-     квалифицированный педагог дополнительного образования, категория которого соответствует профессиональному стандарту «Педагог дополнительного образования»).

2.    Материально-техническое обеспечение.

-     помещение для проведения занятий;

-     дистанционный режим занятий – рабочее место педагога, отвечающего требованиям СанПиН 2.4.2.2821-10, СанПин 2.2.2/2.4.1340-03, охраны труда и здоровья участников образовательного процесса;

-     очный режим занятий – просторный и хорошо освещенный кабинет, оборудованный столами (партами), стульями и шкафами. Количество столов и стульев должно соответствовать количеству обучающихся;

-     компьютер стационарный или ноутбук, подключенные к сети интернет;

-     доска школьная;

-     тетради в клетку;

-     канцелярские принадлежности (ручки, карандаши, линейки, циркуль).

3.    Информационно-методическое обеспечение.

-     Разработанные видео-уроки.

-     Методическая литература для педагога, литература для учащихся.

-     Фонд методических пособий, разработок педагогов.

-     Наглядные пособия.

 

2.3 Формы аттестации

 

Способами определения результативности реализации данной программы являются организация и проведение диагностики уровня сформированности предметных знаний и умений. Выявление уровня усвоения знаний учащимися проводится посредствам проведения промежуточной и итоговой диагностики. При проведении диагностики используются такие формы организации учебного процесса как: тесты, викторины, мониторинг знаний по курсу, выполнение работы на заданную тему, презентация, наблюдение, самоанализ, групповая оценка работ, контрольное задание и т.п.

 

Способы проверки результатов. В процессе обучения детей по данной программе отслеживаются три вида результатов:

-     текущие (цель – выявление ошибок и успехов в работах обучающихся);

-     промежуточные (проверяется уровень освоения детьми программы за полугодие);

-     итоговые (определяется уровень знаний, умений, навыков по освоению программы за весь учебный год и по окончании всего курса обучения).

 

Выявление достигнутых результатов осуществляется:

-     через механизм тестирования (устный фронтальный опрос по отдельным темам пройденного материала);

-     через отчётные просмотры законченных презентаций, проектов.

Отслеживание личностного развития детей осуществляется методом наблюдения и фиксируется в рабочей тетради педагога.

 

 

Для закрепления полученных знаний и умений большое значение имеет коллективный анализ ученических работ. При этом отмечаются наиболее удачные решения, оригинальные подходы к выполнению задания, разбираются характерные ошибки. Оценивается у учащихся умение ставить и решать познавательные и практические задачи, умение самостоятельно решать задачи, примеры и анализировать их. Проверка может быть в устной форме (индивидуальный, групповой опрос), в виде зачетных самостоятельных работ, промежуточных просмотров после выполнения 2-3 работ.

Форма подведения итогов реализации программы – участие в викторине.

 

2.4 Оценочные материалы

Оценка успешности усвоения программного материала проводится в форме наблюдения за учащимися. Данные заносятся в таблицу по каждому разделу программы и оценивается в балах.

1 баллов выставляется за «неверный ответ»;

2 балла – за «не во всём верный ответ»;

3 балла – за «правильный ответ».

2.6. Список литературы

1.    Федеральный Закон Российской Федерации от 29.12.2012 г. № 273 «Об образовании в Российской Федерации» (далее – ФЗ № 273),

2.    Приказ Министерства Просвещения Российской Федерации от 09 ноября 2018 г. № 196 «Об утверждении Порядка организации и осуществления образовательной деятельности по дополнительным общеобразовательным программам»

3.    Концепция развития дополнительного образования детей от 4 сентября 2014 г. № 1726

4.    Методические рекомендации по проектированию дополнительных общеразвивающих программ. Письмо Минобрнауки России от 18.11.15 №09-3242

5.    СанПин 2.4.3172-14: «Санитарно-эпидемиологические требования к устройству, содержанию и организации режима работы образовательных организаций дополнительного образования детей», утверждённый постановлением Главного государственного санитарного врача РФ от 4 июля 2014 года № 41

6.    Гусев В.А., Орлов А.И., Розенталь А.Л. Внеклассная работа с учениками 5-6 классов. - М.: Просвещение,2005.

7.    Журналы «Математика в школе», 1980-2008.

8.    Петрова Ф.Г. Математические вечера: издательство «Удмуртия», Ижевск, 1968.

9.    П.М. Камаев. Устный счёт. М.: Чистые пруды, 2007.(Библиотека « Первого сентября», серия « Математика», №3 (15)/2007

10.              Фарков  А.В. Математические кружки в школе. 5-8 классы– М.  Айрис-пресс, 2006

11.              Фарков А.В. Математические олимпиады в школе. 5-11 классы. М.: Айрис-пресс, 2002.

12.              Фарков  А.В. Внеклассная работа по математике.5-11 классы М.: Айрис-пресс, 2008

13.              Ю.В.Щербакова. Занимательная математика на уроках и внеклассных мероприятиях. 5-8 классы. М.: Глобус.2008.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.7. Соответствие программы нормативным документам

 

Нормативно-правовое обеспечение программы. В настоящее время содержание, роль, назначение и условия реализации программ дополнительного образования закреплены в следующих нормативных документах:

•          Федеральный Закон Российской Федерации от 29.12.2012 № 273 «Об образовании в Российской Федерации» (далее – ФЗ № 273);

•          Концепция развития дополнительного образования детей от 04.09.2014 № 1726-р;

•          Письмо Минобрнауки России от 18.11.2015 № 09-3242 «Методические рекомендации по проектированию дополнительных общеразвивающих программ»;

•          Приказ Министерства просвещения Российской Федерации от 09.11.2018 № 196 «Об утверждении порядка организации и осуществления образовательной деятельности по дополнительным общеобразовательным программам»;

•          Приказ Министерства образования и науки Российской федерации от 23 авгура 2017 г. № 816 «Об утверждении порядка применения организациями, осуществляющими образовательную деятельность электронного обучения, дистанционных образовательных технологии при реализации образовательных программ»

•          СанПин 2.4.4.3172-14: «Санитарно-эпидемиологические требования к устройству, содержанию и организации режима работы образовательных организаций дополнительного образования детей» от 04.07.2014 №41; 

•          СанПин 2.2.2/2.4.1340-03 «Гигиенические требования к персональным электронно-вычислительным машинам и организации работы»;

•          СанПиН 2.4.2.2821-10 "Санитарно-эпидемиологические требования к условиям и организации обучения в образовательных учреждениях" п. 10.18;

•          Устав МБОУ СШ № 29;

•          Локальные нормативные акты.

 

 

Приложение 1

 

Выбор тем и выполнение проектных работ.

Примерные темы проектов:

-     Как люди научились считать.

-      Математика древних народов (Древний Восток: Египет, Вавилон, Китай; Древняя Греция; Индия, страны Ислама). Западная Европа. Математика народов нашей Родины.

-      История математических символов.

-      Мир чисел.

-      История создания кроссвордов.

-      Разновидности кроссвордов.

-      Пентамино.

 

Приложение 2

 

Решение числовых ребусов

Числовые ребусы – это примеры, в которых все или некоторые цифры заменены звёздочками или буквами. При этом одинаковые буквы заменяют одинаковые цифры, разные буквы - разные цифры.

Пусть дан числовой ребус:

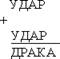Решение:

Число 8126 является решением ребуса, так как при замене буквы У на цифру 8, буквы Д на 1, буквы А на 2, буквы Р на 6 получается верный пример на сложение.

Проверьте, является ли число 5621 решением числового ребуса:

^ УДАР + УДАР = ДРАКА.

 

 

Решите числовой ребус:

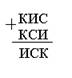
Разберем решение первого ребуса.

Сумма И+С (в разряде десятков) оканчивается на С, но И  О (см. разряд единиц). Значит, И = 9 и 1 десяток в разряде единиц запомнили (решение ниже). Теперь легко найти К в разряде сотен: К = 4. Для С остается одна возможность: С = 5.

 

 

Решите ребус:

Решение:

В ребусе буква Г обозначает цифру 1, так как при сложении двух пятизначных чисел получается шестизначное число. При этом, чтобы произошел переход через десяток в разряде десятков тысяч, буква К должна обозначать цифру 8 или 9 ( меньше 8 буква К обозначать не может, так как буква Г обозначает цифру 1). Буква К заменяется на цифру 8, если при сложении чисел произойдёт переход через десяток в разряде тысяч. Независимо от того будет ли буква К заменена на цифру 8 или 9, буква О должна обозначать цифру 0(нуль). Теперь можно выстроить последовательность замены букв цифрами: Г=1; О=0; Р=5; У=4; К=9; А=8; С=3; Д=7.

Ответ: 94539+10539=105078

 

 

 Приложение 3

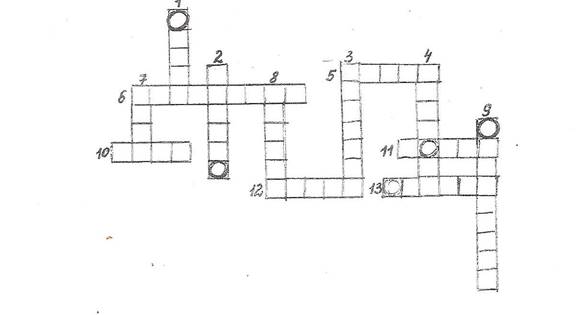Кроссворд на тему «История математики»

 

По горизонтали:

5. Русская дометрическая мера объема жидкостей = 12 л.

6. Русский химик, которому принадлежит заслуга распространения в России метрической системы мер.

10. Старинная мера длины, с 17 в. называлась «четверть аршина»

11.На Руси - волнистая линия, которую ставили над буквами, чтобы не путать их с числами.

12. Специальные знаки, с помощью которых записывают натуральные числа.

13. Единица измерения углов

 

По вертикали:

1. В старину мерная линейка, на которую, обычно, наносили деления в вершках

2. От какого греческого слова происходит слова «метр»

3. Как называются концы каждого звена ломаной

4. Мера «сыпучих» тел («хлебная мера»), которая использовалась на Руси в торговой практике и в быту.

7. Средневековая мера длины в Англии

8. Первый справа класс при записи натуральных чисел.

9. Постоянная величина при рассмотрении математических и др.процессов.

 

 

Ответы: 1. аршин, 2. метрон, 3. вершины. 4. осьмина, 5. ведро, 6. Менделеев, 7. миля, 8. единиц, 9. константа, 10. пядь, 11. титло, 12. цифры, 13. градус.

 

Из выделенных букв составляется слово КНИГА

 

 

 

																						18
																				9
																								19
								8						16
																	10	20
		13					7			17						11				22
				14
1						12			6
														5
								15
				2
																21
													4
	3

Кроссворд по теме «Делимость чисел»

 

 

 

 

По горизонтали: 1. Что является результатом сложения?  2. Числа, используемые при счете, называются …. 3.  Целое положительное число, большее, чем единица, не имеющее других делителей, кроме самого себя и единицы есть … число. 4. Числа 2, 6, 58, 90 и т.п. называются …5. Число, делящееся на данное целое число без остатка называется…… 6. Основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей. 7. Наименьшее из натуральных чисел. 8. Число, которое - в действии деления - подвергается делению. 9. Геометрические фигуры, состоящие из точек и соединяющих их отрезками. 10. Число, которое показывает, сколько раз нужно повторить слагаемым первое число (множимое), чтобы получить произведение. 11. Особенность делимости числа на 2, на 3, на 5, на 9 и на 10 называется …

По вертикали: 12. Натуральное число, большее 1, не являющееся простым. 13. Раздел математики, связанный с изучением количества комбинаций, подчиненных тем или иным условиям. 14. Результатом деления является … 15.  Число, состоящее из одной или нескольких частей (долей) единицы. 16. Величина, получаемая при вычитании из делимого произведения делителя на целое частное. 17.  Наибольшее число, на которое оба числа a и b делятся без остатка называется … общий делитель. 18. Наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания формы объектов. 19. Представление числа в виде произведения множителей. 20. Наименьшее натуральное число, которое делится на m и n без остатка есть … общее кратное. 21. Условное обозначение, предназначенное для записи какого- либо действия. 22. Числа, которые нельзя разделить на 2 без остатка.

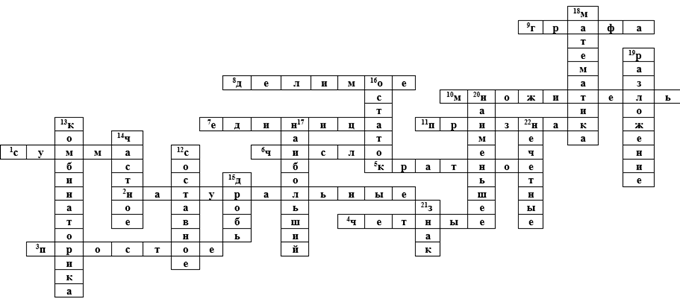Ответы:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 4

 

 

Пентамино

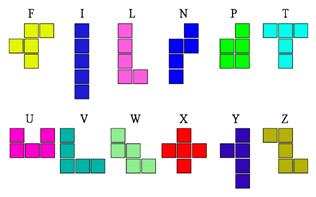
Рис. 5

Полимино, покрывающее пять клеток шахматной доски, называются пентамино. Существует 12 видов пентамино, которые можно обозначить прописными латинскими буквами, как указано на рисунке (см. рис. 5). В качестве приема, позволяющего легко запомнить эти наименования, укажем, что соответствующие буквы составляют конец латинского алфавита (TUVWXYZ) и входят в имя FiLiPiNo. Поскольку всего имеется 12 разных пентамино и каждая из этих фигур покрывает пять клеток, то вместе они покрывают 60 клеток.

Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20 (см. рис. 6).

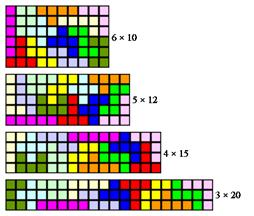
Рис. 6

Для случая 6×10 эту задачу впервые решил в 1965 году Джон Флетчер. Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника, но считая повороты и отражения его частей (иногда внутри прямоугольника образуется симметричная комбинация фигур, поворачивая которую можно получить дополнительные решения).

Для прямоугольника 5×12 существует 1010 решений, 4×15 — 368 решений, 3×20 — всего 2 решения (отличающихся вышеописанным поворотом). В частности, существует 16 способов сложить два прямоугольника 5×6, из которых можно составить как прямоугольник 6×10, так и 5×12.

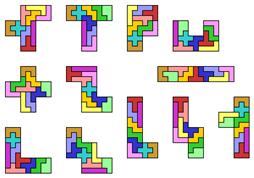
Еще одна интересная задача о пентамино - задача об утроении фигур пентамино (см. рис. 7). Эта задача была предложена профессором Калифорнийского университета Р.М.Робинсоном. Выбрав одну из 12 фигур пентамино, необходимо построить из каких-либо 9 из 11 оставшихся пентамино фигуру, подобную выбранной, но в 3 раза бо́льшей длины и ширины. Решение существует для любого из 12 пентамино, причём не единственное (от 15 решений для Х до 497 для Р). Существует вариант этой задачи, в котором для построения утроенной фигуры разрешается использовать также и саму исходную фигуру. В этом случае число решений от 20 для Х до 9144 для Р-пентамино.

 

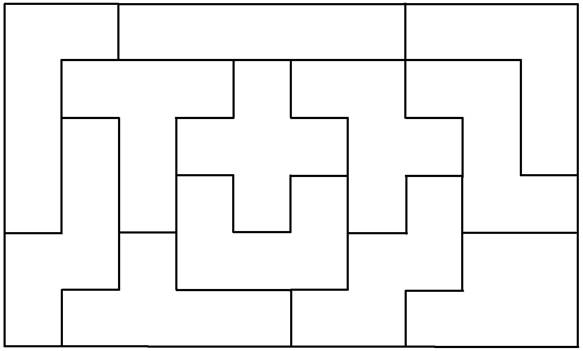Распечатайте вот этот лист и наклейте его на картон. оставьте под прессом (книги, альбомы) до высыхания. Разрежьте детальки. Игра готова.

 

 

 

 

 

 

Приложение 5

 

Танграм (от китайского «семь дощечек мастерства») — головоломка, состоящая из семи танов (плоских геометрических фигур), полученных делением квадрата на семь частей – 2 больших, 2 маленьких и 1 средний треугольник, 1 малый квадрат и параллелограмм, которые складывают определённым образом для получения другой, более сложной, фигуры.

Базовым элементом танграма является тан. Таны возможно получить при разрезании квадрата первоначально на два больших равных треугольника, далее согласно рисунка. Минимальное количество базовых фигур равное семи приводит к гениальной простоте комбинаций. Для изготовления танграма понадобится шаблон головоломки, цветной картон, ножницы. Также можно изготовить головоломку из пластиковых коробочек от компакт-дисков или фанеры.

 

 

 

 

 

 

Правила игры:

Классические правила танграма очень просты. Игра заключается в сложении из деталей головоломки геометрических фигур, букв, цифр, силуэтов животных, растений, людей, предметов – всего, что подскажет фантазия.

-     в каждую собранную фигуру должны входить все семь элементов,

-     при составлении фигур элементы не должны накладываться друг на друга,

-     элементы фигур должны соприкасаться друг с другом,

-     начинать нужно с того, чтобы найти место самого большого треугольника.

В результате игры получается плоскостное силуэтное изображение. Оно весьма условно, но образ легко угадывается по основным характерным признакам предмета: его строению и форме.

 

 

 

 

 

 

 

Скачано с www.znanio.ru