Дополнительная образовательная программа "Отдельные вопросы математики, способствующие углублению знаний учащихся"

Данная программа способствует интеллектуальному и творческому развитию учащихся, формированию уровня абстрактного и логического мышления.Особенностью курса является то, что приобретенные знания способствуют сдачи ГИА на более высоком уровне.Изучение темы не связаны жестко друг с другом, что допускает возможность перестановки изучаемых тем.основные цели и задачи, заявленные в программе, направлены на прочное и сознательное овладение учащимися системой математических знаний и умений при решении заданийДанная программа способствует интеллектуальному и творческому развитию учащихся, формированию уровня абстрактного и логического мышления.Особенностью курса является то, что приобретенные знания способствуют сдачи ГИА на более высоком уровне.Изучение темы не связаны жестко друг с другом, что допускает возможность перестановки изучаемых тем.основные цели и задачи, заявленные в программе, направлены на прочное и сознательное овладение учащимися системой математических знаний и умений при решении заданий

МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ЛИЦЕЙ №19»

ГОРОДСКОГО ОКРУГА ТОЛЬЯТТИ

«Утверждаю» Директор МОУ лицея №19 г.о. Тольятти
Д.С Кизилов « » 200 г.

Программа принята на основании Решения педагогического совета МБУ «Лицея»№19 Протокол № от ___________

ДОПОЛНИТЕЛЬНАЯ ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА

«ОТДЕЛЬНЫЕ ВОПРОСЫ МАТЕМАТИКИ, СПОСОБСТВУЮЩИЕ УГЛУБЛЕНИЮ ЗНАНИЙ УЧАЩИХСЯ»

Возраст обучающегося – 7-9 класс

Срок реализации – 6лет

Автор (составитель):

Резцова Ирина Александровна

Анищенко Светлана Геннадьевна

педагоги дополнительного

образования

Тольятти, 2019

Рецензия

На авторскую программу Резцовой И.А. Анищенко С.Г. «Отдельные вопросы математики, способствующие углублению знаний учащихся» для 7-9 класса (пропедевтический курс)

Реализуемая программа по математике состоит из пояснительной записки, требований к математической подготовке учащихся, содержания обучения и тематического планирования.

Анализ содержания программы позволяет констатировать ее соответствие программам по математике для пропедевтического изучения.

Содержание курса и методика его изучения позволяет усвоить, углубить и расширить знания методов, приемов и подходов к решению задач.

Данный курс способствует интеллектуальному и творческому развитию учащихся, формированию уровня абстрактного и логического мышления.

Особенностью курса является то, что приобретенные знания способствуют сдачи ОГЭ на более высоком уровне.

Изучаемые темы не связаны жестко друг с другом, что допускает возможность перестановки изучаемых вопросов.

Основные цели и задачи, заявляемые в программе, направлены на прочное и сознательное овладение учащимся системой математических знаний и умений при решении заданий.

Таким образом, программа удовлетворяет всем основным требованиям к программам для пропедевтического изучения математики в 7-9 классах.

Программа рекомендована к использованию.

Рецензент Утеева Роза Азербаевна доктор педагогических наук. профессор кафедры «Высшая математика и математическое образование» . Заведующая кафедрой.

Пояснительная записка

Одной из важнейших задач школы является воспитание всесторонне развитого человека, воспринимающего мир как единое целое.

В настоящее время введение дополнительных услуг широко используется образовательными учреждениями и позволяет учителям математики более детально проработать курс. Следует отметить, что занятия ДОУ должны быть направлены не только на закрепление пройденного материала, но и на расширение знаний учащихся. Дополнительные образовательные услуги призваны помочь учащимся осознать степень интереса к предмету и оценить возможности овладения им на углубленном уровне. Этот курс дает возможность подготовиться к изучению курса углубленной математики в последующих классах. В программу включена тема «задачи на построение», т.к. ее изучение позволяет обобщить геометрический материал 7-8 классов.

Цели:

o Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

o Развитие таких качеств личности, как ясность и точность мысли, логическое мышление, пространственное воображение, алгоритмическая культура, интуиция, критичность и самокритичность;

o Формирование представлений об идеях и методах математики как универсального языка науки и техники, средстве, моделирования процессов и явлений;

o Воспитание средствами математики культуры личности.

Ожидаемые результаты:

В результате внедрения предлагаемой программы для дополнительных образовательных услуг по математике будут сняты трудности в систематическом изучении этого курса и повешение усвоения учащимися в будущем основного материала, а так же поможет учащимся сдать Государственную Итоговую Аттестацию на более высоком уровне.

Программа рассчитана на 34 часа в год.

7 класс:

Глава I. Нестандартные задачи по теме множества.– 6 часов

Глава II. Свойства и признаки делимости чисел на 4, 9, 11, 25. Деление с остатком. – 8 часов

Глава III. Преобразование рациональных выражений. Квадрат суммы нескольких слагаемых. Разность n-х степеней. – 9 часов

Глава IV. Преобразование дробно-линейной функции и построение ее графиков. – 6 часов

Глава V. Задачи на построение – 5 часов

8 класс:

Глава I. Понятия равносильности уравнений и неравенств – 8 часов

Глава II. Решение дробно-рациональных уравнений и неравенств, и неравенств содержащих переменную под знаком модуля. – 10 часов

Глава III. Преобразование выражений содержащих квадратные корни. Преобразование двойных радикалов. – 8 часов

Глава IV. Выражения, симметрические относительно корней квадратного уравнения, их связь с коэффициентами. Решение задач повышенной сложности с помощью уравнений. – 4 часа

Глава V. Уравнения с параметрами – 4 часа

9 класс:

Глава I. Функции, их свойства и графики: y = [x] и y = {x}; y =-f(x), y = f(-x), y = -f(-x);

y = |f(x)| и y = f(|x|) - 8 часов

Глава II. Решение систем линейных уравнений методом Гаусса и методом Крамера. – 10 часов

Глава III. Неравенства и системы неравенств с переменными содержащими знак модуля. – 8 часов

Глава IV. Последовательности. Метод математической индукции. – 8 часов.

Календарно-тематическое планирование 7 Класс

№ п/п	Разделы, темы	Компетентности	Количество часов	Теория	Практика
I.	Нестандартные задачи по теме множества. 1. Множество и элемент множества 2. Подмножество 3. Пересечение и объединение множеств 4. Взаимно однозначное соответствие 5. Свойства числовых множеств	Иметь представление о множествах и операциях над ними, понимать и применять соответствующую символику. Уметь приводить примеры конечных и бесконечных множеств, иллюстрировать на примерах, как можно установить взаимное однозначное соответствие между некоторыми бесконечными множествами.	6	2	4
II.	Делимость чисел 1. Понятие делимости 2. Делимость суммы и произведения 3. Признаки делимости на 2,3,4,5 и 9 4. Признаки делимости на 11 5. Частное и остаток 6. Свойства деления с остатком	Уметь применять понятие делимости для решения задач повышенной сложности. Уметь проводить дедуктивные рассуждения на алгебраическом материале. Уметь подбирать пары равноостаточных чисел.	8	3	5
III.	Рациональные выражения 1.Приемы преобразования целого выражения в многочлен 2. Возведение двучлена в степень 3. Квадрат суммы нескольких слагаемых 4. Приемы разложения многочлена на множители 5. Разность n-х степеней 6. Преобразование рациональной дроби 7. Действия с рациональными дробями	Уметь выводить формулы сокращённого умножения: куба двучлена, квадрата суммы нескольких слагаемых. Знать метод неопределенных коэффициентов, формулы разности n-х степеней и суммы нечетных степеней, применять эти знания к разложению многочлена на множитель и содержательным задачам, в которых эти методы используются.	9	3	6
IV.	Функции и их графики 1. Функция. Область определения и область значений функции 2. Способы задания функции 3. Простейшие преобразования графиков функций 4. Дробно-линейная функция и ее график	Уметь применять символику, связанную с понятием функции, иметь представление о графиках кусочно-заданных функций.	6	2	4
V.	Задачи на построение	Уметь решать задачи на построение.	5	2	3

Календарно-тематическое планирование 8 класс:

№ п/п	Разделы, темы	Компетентности	Количество часов	Теория	Практика
I	Равносильность уравнений и неравенств 1. Высказывания и предложения с переменными 2. Понятие о следовании и равносильности 3. Равносильные уравнения и уравнения-следствия 4.Равносильные системы уравнений 5. Равносильные неравенства и неравенства- следствия	Уметь решать уравнения и неравенства с одной переменной, а также с двумя переменными и их системы. Уметь соотносить между множествами истинности предложений с переменными, связанных отношениями следования или равносильности.	8	2	6
II	Уравнения и неравенства с одной переменной 1. Целые уравнения и способы их решения 2. Решение дробно-рациональных уравнений 3. Решение рациональных неравенств 4. Расстояние между точками координатной прямой 5. Решение уравнений, содержащих переменную под знаком модуля 6. Решение неравенств, содержащих переменную под знаком модуля 7. Решение иррациональных уравнений 8. Решение иррациональных неравенств	Уметь решать уравнения и неравенства с переменной под знаком модуля. Уметь использовать новые по сравнению с основным курсом приемы решения уравнений (введение новой переменной, исключение из дроби целой части, группировка отдельных членов уравнения и др.), которые позволяют более рационально решать уравнения. Уметь использовать способ решения иррациональных неравенств с помощью введения новой переменной.	10	4	6
III	Квадратные и кубические корни 1. Арифметический квадратный корень. Функция 2. Свойства арифметического квадратного корня и их применение в преобразованиях 3. Преобразование двойных радикалов 4. Кубический корень и его свойства 5. Функция и ее график	Уметь преобразовывать иррациональные выражения. Иметь представление о двойных радикалах, при освобождении которых должны пользоваться разными приемами: методом подбора и методом неопределенных коэффициентов.	8	3	5
IV	Квадратные уравнения 1. Теорема Виета 2. Выражения, симметрические относительно корней квадратного уравнения, их связь с коэффициентами 3. Исследование квадратного уравнения 4. Решение задач с помощью уравнений	Уметь использовать формулу Виета там, где это целесообразно. Уметь решать «задачи на смеси», «задачи на сложные проценты»	4	2	2
V	Уравнения с параметрами 1. Что значит решить уравнение с параметром 2. Решение линейных и квадратных уравнений с параметрами 3. Решение дробно-рациональных уравнений, содержащих параметры 4. Решение задач с параметрами	Уметь решать уравнения с параметрами, записывать ответ как составную часть решения уравнения	4	2	2

Календарно-тематическое планирование 9 класс:

№ п/п	Разделы, темы	Компетентности	Количество часов	Теория	Практика
I	Функции, их свойства и графики 1. Четные и нечетные функции 2. Монотонные функции 3. Ограниченные и неограниченные функции 4. Исследование функций элементарными способами 5. Построение графиков функций 6. Графики функций 7. Графики функций 8. Графики функций	Уметь выполнять построение графиков более сложных функций и их исследования. Ознакомить с понятием разрывной функции, и ввести понятие «точка разрыва» Уметь преобразовывать графики функций вида	8	3	5
II	Уравнения с двумя переменными и их системы 1. Уравнение с двумя переменными и его степень 2. Уравнение с двумя переменными и его график 3. Графическая интерпретация решения систем уравнений 4. Способы решения систем уравнений с двумя переменными	Знать все виды кривых и их различное расположение на координатной плоскости. Уметь решать системы уравнений второй степени, которые позволяют ознакомить учащихся с различными приемами решения систем уравнений.	10	4	6
III	Неравенства с двумя переменными и их системы 1. Линейные неравенства с двумя переменными 2. Системы линейных неравенств с двумя переменными 3. Неравенства и системы неравенств высших степеней с двумя переменными 4. Неравенства и системы неравенств с переменными под знаком модуля	Уметь решать задания на геометрическую интерпретацию множества решений линейного неравенства или системы линейных неравенств с двумя переменными, а так же задания, в которых требуется охарактеризовать неравенством или системой неравенств некоторую фигуру на координатной плоскости. Уметь решать более сложные примеры неравенств с двумя переменными и их системы.	8	4	4
IV	Последовательности 1. Числовые последовательности. Способы задания последовательностей. 2. Арифметическая и геометрическая прогрессии	Уметь изображать члены последовательности на координатной прямой и на координатной плоскости.	8	3	5

Список использованной литературы

1. Ю.Н. Макарычев, Р.Г. Миндюк. Дополнительные главы к школьному учебнику . М . «Просвещение» . 2006г; 8 класс

2. Н.Я. Виленкин и др. Алгебра. Учебник для учащихся 9 класса с углублённым изучением математики. М. «Просвещение». 2003г.

3. А.О Корнеева. Геометрические построения в курсе средней школы. Сартов. «Лицей». 2003г.

4. Ю.Н. Макарычев , Н.Г. Миндюк . Дополнительные главы к школьному учебнику. М. «Просвещение» 2004г. 9 класс.

5. Н.Я. Виленкин и др. Алгебра. Учебник для учащихся 9 класса с углублённым изучением математики. М. «Просвещение». 2004г.

6. М.Х. Болдырева, Ю.П. Карпухин, Г.А. Клековкин. Факультативные занятия по математике в 9 классе, Самара 2002г.

7. Ф.Ф. Лысенко. Подготовка к итоговой аттестации. 2008,2009г.

8. М.Н. Кочагина. Сборник заданий 9 класс. М.:Эксмо 2008г. Математика ГИА.

9. Г.А. Клековин, В.А Гаранин. Задачи повышенной трудности по геометрии. Самара 2002г.

10. Е.А. Воробьва. Алгебра 9 класс. Тренировочный вариант к экзамену в новой форме. Саратов» Лицей, 2009г.

11. Г.В. Колесникова, С.С. Минаева. ЕГЭ. Математика 9 класс. Типовые тестовые задания.-М.:Издательство «Экзамен», 2007г.

12. Л.Д. Лаппо. ЕГЭ. Математика 9 класс. Практикум по выполнению типовых тестовых заданий.-М: «Экзамен»2007г.

13. Ф.Ф. Лысенко. Алгебра. Тесты для промежуточной аттестации 7-8 класс. Ростов-на-Дону: Легион, 2007-2008г.

14. Л.В. Кузницова. Алгебра. Сборник заданий для итоговой аттестации 9 класс, М. Просвещение, 2007г.

15. Т.М. Ерина. Алгебра. Экспериментальная экзаменационная работа. Практикум 8 класс.М.: «Экзамен», 2009г.

Равносильность уравнений и неравенств.

Практическая работа №1.

1. Найдите множество значений х, при которых выражение имеет смысл:

а) +	а)

2.Укажите множество натуральных значений переменной n, при которых обращается в истинное высказывание предложение:

а) n кратно 5 и не превосходит 27

а) n является делителем 32 и 36

3. Решите уравнение:

4. При каких значениях а имеет решение система уравнений:

5. Докажите, что любое число является решением неравенства:

a) 5x(x – 11) – (6x +4)(x – 1) < 7 – 53x

a) (2x – 1)(2x +1) – 4(x +1) +16 > 0

Уравнения и неравенства с одной переменной

Практическая работа №2.

1. Решите уравнения:

2.Укажите два каких-нибудь целых решения неравенств:

а)

3. Решите уравнение:

4. Решите неравенство:

5. Решите уравнение:

б)

Квадратные и кубические корни.

Практическая работа №3.

1. Решите уравнение:

а)

б)

в)

а)

б)

в)

2.Освободитесь от иррациональности в знаменателе дроби:

а)

б)

а)

б)

3. Найдите значение выражения:

а)

4. Упростите выражение:

а)

б)

а)

б)

5. Найдите значение выражения:

a) , при a= - 1,2

a) , при x = - 2

Квадратные уравнения.

Практическая работа №4.

1. Решите уравнение:

а)

2.Найдите корни уравнения и коэффициент p, если известно, что:

а) сумма квадратов корней уравнения равна 96

а) сумма квадратов корней уравнения

равна 234

3. При каких значениях a уравнение имеет единственный корень:

а)

4. Решите задачу:

а) От прямоугольного листа картона, имеющего длину 70 см. и ширину 80 см., отрезали по углам равные квадраты и из оставшейся части склеили коробку.

Найдите сторону квадрата, если известно, что основание коробки имеет площадь 20

а) Положив в банк деньги, вкладчик получил через год прибыль 240 тысяч рублей. Однако, он не стал забирать деньги из банка, а, добавив к ним еще 60 тысяч, снова оставил деньги на год. В результате спустя еще год он получил в банке 1 миллион 100 тысяч рублей. Какая сумма была положена в банк первоначально и какой процент прибыли в год давал банк?

5. Пусть и- корни уравнения . Найдите:

Множества и операции над ними.

Проверочная работа №1.

1. Запишите путем перечисления элементов множества:

а) A= а) B=

б) C= б) C=

2. Решите задачу:

3. Проверьте, верно ли высказывание «a», если:

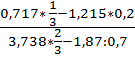а) a = а) a =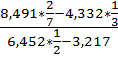

4. Найдите множество общих натуральных делителей числа:

а) 30 и 45 а) 15 и 45

5. Начертите четырехугольник и треугольник так, чтобы в пересечении их сторон оказалось:

а) 2 точки а) 3 точки

Свойства делимости.

Проверочная работа №2.

1. Найдите пересечение:

I) Множество четных чисел и множества чисел, кратных 4.

II) Множества чисел кратных 3, и множества чисел кратных 7.

2. Найдите объединение:

I) Множества чисел кратных 6, и множества чисел кратных 3.

II) Множества чисел кратных 15, и множества нечетных чисел.

3. Докажите, что:

а) 6¹⁴+ 36⁸, делится на 37 а) 25⁵⁰– 5⁹⁹, делится на 4

б) 3¹²– 9⁵ + 27³, делится на 25 б) 4¹² – 2²⁰ + 8⁶, делится на 61

4. Какие из данных чисел 7194, 18456, 36735, 17214, 781120, делятся:

а) на 6 а) на 15

5. Замените * цифрой так, чтобы:

а) число 26873* делилось на 22 а) число 187674* делилось на 33

6. Какой остаток получается при делении:

а) 3¹⁷ на 10 а) 7⁴ на 5

Рациональные выражения.

Проверочная работа №3.

1. Выполните умножение:

а) (x-1)(x⁴+x³-x²+x-1) а) (x³+2x²+3x+4)(x-1)

б) (a³-2a²-3a-5)(3a²-4a+1) б) (a⁴+2a³+3a²-4a-10)(a²-2a+5)

2. Представьте в виде многочлена:

а) (x-1)⁴ ; б) (x+1)⁵ ; в) (y-2)⁶ а) (y+2)⁴; б) (y-2)⁵; в) (x-1)⁶

3. Упростите выражение:

а) (3a+2b-1)²+(3a-2b+1)² а) (5a+b+2)²-(5a-b-2)²

4. Разложите на множители трехчлен:

а) x²+8x+12 а) x²+13x+40

б) x²-11x+28 б) x²+4x-21

5. Выполните умножение:

а) * а) *

Функции и их графики.

Проверочная работа №4.

1. Функция задана формулой f(x) = 2x – 1

а) Найдите f(-2), f(0) а) Найдите f(2), f(-2,5)

б) Найдите значение аргумента, при котором:

б) f(x) = 9 б) f(x) = -23

2. Постройте график функции, если:

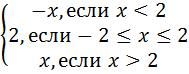а) y = а) y =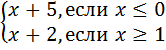

Какова область определения каждой функции?

3. Постройте график функции:

а)y = x²+2 а)y = x²-3

б)y = (x-1)² б)y = (x+2)²

в)y = (x+1)²-2 в)y = (x-2)²+1

4. Какова область определения функции:

а)y = а)y =

б)y = б)y =

в)y = в)y =

5. Используя график функции y = , постройте график функции, выполнив сдвиги этой гиперболы:

а) а)

Функции, их свойства и графики.

Практическая работа №1.

1. Известно, что f(x) = x¹⁰⁵, а g(x) = x¹⁰⁰. Сравните:

а) f(-2) и g(2) а) f(-3) и g(3)

б) f(5) и g(5) б) f(-5) и g(-5)

2. Определите характер монотонности функции:

а) y = а) y =

3. Найдите область определения функции:

а) y = а) y =

б) y = б) y =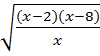

4. Проведите исследование и постройте график функции:

а) f(x) = а) f(x) =

5. Постройте график функции:

а) y = а) y =

Уравнения с двумя переменными и их системы

Практическая работа №2

1. Найдите все целые решения уравнения:

а) x² + 2xy - 3y² = 5 а) x² + 9xy + 8y² = 8

2.Докажите, что графиком уравнения является окружность:

а) x² + y² – 4x + 6y – 12 = 0 а) x² + y² – 2x – 4y – 4 = 0

3. Решите графически систему уравнений:

а) 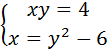а)

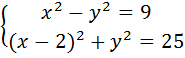
4. Решите систему:

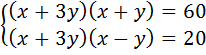а) а)

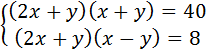
5. Найдите множество решений системы:

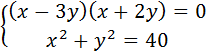а) а)

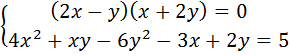
Неравенства с двумя переменными и их системы

Практическая работа №3

1. Изобразите плоскость, которую задает неравенство:

а) 4x + y – 2 < 0 а) 3x – y + 1 > 0

б) 2x + 3y + 6 ≥ 0 б) x – 2y – 2 ≤ 0

2. Выясните, какое множество точек задает на координатной плоскости система неравенств:

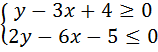а) а)

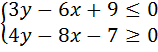
3. Решите задачу:

I) Постройте треугольник с вершинами A(4;0), B(-2;0), C(3;-2) и задайте его системой неравенств.

II) Постройте четырехугольник с вершинами A(0;5), B(4;0), C(1;-2), D(-4;-2) и задайте его системой неравенств.

4. Изобразите на координатной плоскости множество решений неравенства и укажите какие-либо 2 точки, принадлежащие этому множеству:

а) y ≤ x² – 5x а) y > 2x² + 5x - 12

5.Изобразите множество точек, координаты которых удовлетворяют системе неравенств:

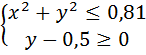а) а)

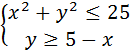
Последовательности.

Практическая работа №4.

1) Запишите первые шесть членов последовательности (b_n) заданной рекуррентным способом.

а) b₁ = 5, b_n₊₁ = b_n + 4 а) b₁ = 8, b_n₊₁ = 12 – b_n

2) Докажите, что последовательность (x_n) является возрастающей, если:

а) x_n = 6(2n-1) а) x_n=

3) Выясните, является ли последовательность (a_n) возрастающей или убывающей, если:

а) a_n = а) a_n =

4) Является ли арифметической прогрессией последовательность (a_n) заданная формулой:

а) a_n = 5n + 1 а) a_n = 3,6 - n

5) Является ли геометрической прогрессией последовательность (y_n) заданная формулой:

а) y_n = -5 * 2ⁿ⁺³ а) y_n = 2ⁿ⁺¹ * 3ⁿ⁺²

МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ

Рецензия На авторскую программу

Пояснительная записка Одной из важнейших задач школы является воспитание всесторонне развитого человека, воспринимающего мир как единое целое

Глава I . Нестандартные задачи по теме множества

Календарно-тематическое планирование 7

III . Рациональные выражения 1

Календарно-тематическое планирование 8 класс: № п / п

Решение неравенств, содержащих переменную под знаком модуля 7

V Уравнения с параметрами 1

Календарно-тематическое планирование 9 класс: № п / п

II Уравнения с двумя переменными и их системы 1

Список использованной литературы 1

Равносильность уравнений и неравенств

Уравнения и неравенства с одной переменной

Квадратные и кубические корни

Квадратные уравнения. Практическая работа №4

Множества и операции над ними

Свойства делимости. Проверочная работа №2

Рациональные выражения. Проверочная работа №3

Функции и их графики. Проверочная работа №4

Функции, их свойства и графики

Уравнения с двумя переменными и их системы

Неравенства с двумя переменными и их системы

Последовательности. Практическая работа №4

Дополнительная образовательная программа "Отдельные вопросы математики, способствующие углублению знаний учащихся"

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

06.11.2018