Дополнительные возможности электронных таблиц Microsoft Excel: поиск решения

Урок по теме “Дополнительные возможности электронных таблиц Microsoft Excel: поиск решения”

11класс

Раздел программы: “ Информационные технологии”.

Тема урока: “Дополнительные возможности электронных таблиц Excel: принятие решения”.

Тип урока:  обобщающий урок

Вид урока: урок-практикум, продолжительность 1.5 часа (сдвоенный урок - два урока по 45 минут)

Технология: проблемно-исследовательская

 

Цели урока:

1. Закрепление навыков общенаучного подхода к решению задач методом моделирования.
2. Развитие творческого, критического, операционного мышления.
3. Обучение использованию встроенных возможностей Excel для решения задач оптимизации.

 

Задачи урока:

1. Воспитательная:

-          воспитание у учащихся умения самостоятельно и творчески работать с конкретным приложением (информационная культура), критически осмысливать результаты своей деятельности.

2. Развивающая:

-          развитие творческих способностей учащихся, познавательного  интереса и положительной мотивации обучения, расширение кругозора;

3 .Образовательная:

-          закрепление и обобщение пройденного материала по теме “Компьютерное моделирование”;

-          закрепление основных навыков работы с электронными таблицами Excel;

-          обучение загрузке и применению надстройки Microsoft Excel  “поиск решения”;

 

Оборудование и дидактические материалы:

-          компьютерный класс;

-          приложение Microsoft Excel;

-          тест по теме “Компьютерное моделирование”;

-          практические задания на проверку навыков работы с приложением Excel;

-          текст задачи.

-           

План урока (время):

-          Организационный момент (1 минута).

-          Актуализация знаний (10+10 минут+1 минута на смену заданий).

-          Обсуждение теста и практической работы (5 минут)

-          Объяснение возможностей инструмента «поиск решения» (4 минуты)

-          Индивидуальная  работа за компьютером (14 минут)

-          Перемена 10 минут.

-          Формулировка задачи оптимизации (2 минуты)

-          Постановка задачи и ее обсуждение (12-15 минут)

-          Выполнение учащимися практической работы по оптимизации (20минут)

-          Подведение итогов урока, домашнее задание       ( 5 минут).

-          Упражнения для глаз (2-3 минуты)

Ход урока:

 

1. Организационный момент. Объявление темы и целей урока.

Сегодня мы повторим материал прошлых уроков, связанный с применением электронных таблиц Excel , а также обсудим проблемы, связанные с общим подходом к решению различных жизненно важных задач.

Кроме того, вы научитесь с помощью электронных таблиц Excel не только подбирать параметры для получения нужного решения, но и организовывать сам поиск решения.

2. Выполнение теста и практической работы для повторения и закрепления полученных навыков.

Учитель: на рабочих столах лежат тестовые задания, а на столах рядом с компьютерами задания на практическую работу.( Поскольку в компьютерном классе установлено всего 8 персональных компьютеров, делимся пополам – первая половина берет задания для выполнения в среде приложения Excel, вторая – тесты по компьютерному моделированию. -  это привычно и не требует пояснений со стороны учителя)  Время выполнения 10 минут (обычно учащиеся справляются быстрее). Затем подгруппы меняются местами.

Внимание: результаты практической работы сохранить в папку своего класса, имена файлов – ваши фамилии;

ответы к тестам пишем на листах, разложенных вместе с текстами тестов.

При выполнении практической работы можете совещаться, при выполнении теста нет.

(см. приложения 1 и 2)

3. Обсуждение полученных результатов.

а) по тестированию:

 вопрос 1: почему неприемлем вариант б? Ответ: потому что модель – представление, замещение одного объекта другим, а не создание представления о нем.

                        почему неприемлем вариант в? Ответ: потому что модель далеко не всегда упрощенное представление оригинала, например, современные японские роботы являются моделью человека не только в повторении некоторых внешних признаков, но и в поведении. Их устройство чрезвычайно сложное, при их создании используются достижения современной электроники и кибернетики. Модель беднее прототипа, поскольку при ее создании отбрасываются те характеристики оригинала, которые несущественны для решения поставленной задачи, либо которые по каким-либо причинам мы не можем учесть.

  вопрос 2: почему неприемлем вариант а? Ответ: непонятно, что значит детальное описание? На каком-то языке? Или это рисунок? Что значит максимальная информация? Для какой задачи она максимальна?

            почему неприемлем вариант б? Ответ: неясно, что значит “совокупность информации”

вопрос 3: почему неприемлем вариант а? Ответ: потому что в математическую модель могут быть включены не только уравнения, но и неравенства, различные другие условия.

               почему неприемлем вариант б? Ответ: математическая модель – частный случай информационной модели, но не наоборот. Например наш классный журнал – это информационная модель класса, но не математическая модель его.

вопрос 4: почему неприемлем вариант б? Ответ: потому что программа определяет набор действий для решения задачи, но далеко не всегда содержит все необходимые параметры для решения задачи, например наборы файлов с данными, библиотеки и т.д.

               почему неприемлем вариант в? Ответ: неясна форма описания компьютера – может это Price-лист? В нем  ведь тоже содержится описание различных устройств и их характеристик.

вопрос 5:

Ожидаемый ответ: нет, поскольку не заданы ограничения на параметры.

Исходя из физического смысла параметров, U>=0 и R>0. Случай сверхпроводимости не рассматриваем. Задача расчета силы тока поставлена, если указано :

          рассчитать I=U/R при U>=0 и R>0. Если ограничения на значения параметров

           U и R не выполняются, расчет по формуле не выполнять и предупредить о

          невозможности решения задачи.

Вторая задача поставлена, если указано:

          рассчитать y=a/b при b<>0. При b=0 предупредить о невозможности решения.

б) по практическому заданию:

По первой части задания у вас получилось, что надо бы заработать еще 4 пятерки и все ОК. А во по «троечкам» нечто странное – их количество стало отрицательным. В чем дело?

Ответ: задача плохо поставлена – связи между параметрами в формуле указаны, а вот ограничения на их значения – нет.

Вопрос: А была ли у вас возможность эти ограничения указать?

Ответ: нет, в окне команды “подбор параметра” такой возможности нет.

Учитель: хорошо, в Excel есть инструмент для решения и таких задач.  Он называется “поиск решения” и находится там же, где и подбор параметра: в пункте меню “Сервис”.

Если вы его там не нашли, войдите в “надстройки” и поставьте «галочку» напротив строки «поиск решения». Иногда для доустановки этого компонента требуется компакт-диск с приложениями Microsoft Office.

Давайте попробуем воспользоваться этим инструментом.

4. Использование  инструмента «поиск решения»

Учитель садится за компьютер и объясняет, каким образом применять этот инструмент с вариантами ограничений на  значения параметров:

все они – целые, количество двоек и троек мы оставим в покое, а вот четверки и пятерки допускаем варьировать. Демонстрируется возможность добавления, изменения и удаления ограничений. Подчеркивается, что при каждом из этих действий модель задачи изменяется.

В печатном виде возле каждого компьютера находится инструкция по применению надстройки «поиск решения».

Учащиеся по 2 человека садятся за компьютеры и применяют полученные инструкции.

Учитель помогает, далее расширяется количество изменяемых параметров, включая все оценки – оказывается, что одно из решений, - когда количество двоек=0, но увы, в задаче зафиксировано текущее состояние оценок по предмету, выбор учеником сделан и его знания были оценены неудовлетворительно. Так что думайте, детки, не ставьте себя сами в затруднительное положение.

До конца 1-го часа занятий учащиеся работают с моделью успеваемости.

5. Решение задачи оптимизации. Моделирование и формализация.

Начало второго урока.

Задача:

Группа туристов возвращается из похода и должна попасть в город, чтобы успеть на последнюю электричку.

Вопрос: можно ли считать, что задача поставлена?

Ответ: нет, поскольку пока только описана ситуация и поставлена цель – быстрее попасть в город.

Вопрос: в чем будет заключаться постановка задачи?

Ответы учащихся: сначала надо собрать информацию о месте нахождения группы, оценить расстояние до города, возможности передвижения – пешком или на транспорте, сколько осталось времени до отхода электрички.

Вопрос:  какие источники информации можно использовать?

Ответы: карты местности, опрос местных жителей или других туристов, компас для определения направления, расписание движения электричек, часы.

Учитель: в результате активной суеты всех членов группы туристов получены следующие данные, которые можно считать вполне достоверными:

 

В настоящий  момент группа находится в поле и расстояние до города по прямой составляет 3 км. Через город проходит хорошая дорога, известно кратчайшее расстояние от места нахождения группы до дороги  - 6 км. Скорость передвижения по полю 4 км/час, а по дороге 5 км/час. До отхода последней электрички осталось 1 час 45 минут.

 Какой маршрут выбрать группе, чтобы быстрее попасть в город?

(текст задачи в этой формулировке раздается всем учащимся)

 

Учитель: направлены ли действия группы по сбору данных на моделирование задачи достижения цели в кратчайшее время?

Ответ: да, поскольку мысленно каждый турист наверняка представляет себе модель задачи и целенаправленно собирает данные не о перспективах на погоду или урожай в данной местности,

не о фауне (здесь смех –«волка боюсь!») или флоре и т. п.

Учитель: итак, мы строим модель задачи, преобразуя ее из мысленного, интуитивного образа в некоторую форму, чтобы можно было обсуждать.

Вопрос: как называется этот процесс?

Ответ: формализация задачи – мы выделяем наиболее важные для решения задачи параметры и попытаемся установить между ними связь.

Учитель: первая часть постановки задачи уже есть – задача сформулирована и известны значения необходимых параметров. Чтобы лучше представить себе ситуацию построим графическую модель взаимного расположения объектов задачи – сделаем чертеж. Очень часто именно графическое, более наглядное, чем словесное, отображение задачи, помогает в ее решении.

 

           х  о  р  о  ш  а  я            д  о  р  о  г  а

х

       о

       р

п     о     л     е

       о

       ш

       а

       я

дорога

 

 

 

 

Очевидно, что возможны три варианта решения:

1. Идти по полю.
2. Идти сразу на дорогу кратчайшим путем, а затем по дороге до города.
3. Идти часть пути по полю, а затем по дороге.

Соотнесем наши рассуждения с чертежом

АС=6 км

АВ=3км

скорость перемещения по полю Vp=4 км/час

скорость перемещения по дороге Vd=5 км/час

Вопрос: как теперь насчет формализации задачи?

Ответ: степень формализации задачи увеличилась, мы ввели формальные обозначения из языка математики.

Вопрос: а нет ли каких-либо отклонений в нашем чертеже от реальной жизненной ситуации?

               И в какой мере допустимо пренебречь чем-то?

Ответ: да, особенно про поле – вряд ли можно двигаться точно по прямой;

            да, ведь Земля круглая. Примем эти допущения, т. к. расстояния в данной задаче невелики по сравнению с размером Земли, а насчет формы нашего пути – пусть туристы стараются не сбиваться.

Учитель: можно ли сказать, что теперь модель задачи построена?

Ответ: нет, т.к. не указана связь между параметрами. И надо ввести еще один параметр – время.

Учитель: попробуйте установить эту связь. Можете для удобства обозначить расстояние BD через х, иногда и привычная форма обозначения помогает быстрее решать.  В остальном  дальнейшая формализация для вас не должна представлять трудности.

После недолгой самостоятельной работы появилась модель задачи в следующем виде (ее записали на доске):

Время достижения города по дороге td=(AB+BC)/Vd

Время достижения города по полю tp=AC/Vp

Время достижения города по траектории ADC t=AD/Vp+DC/Vd

Расстояния: AD=(AB²+BD²)^0.5

                      DC=BC-BD.

Очевидно, что должны выполняться следующие ограничения:

                       BD>0  и  BD<BC.

Вместе с числовыми значениями параметров расстояний и скоростей эти уравнения и неравенства представляют информационную модель задачи, более точно – математическую модель.  Модель построена, задача поставлена. Наша цель – найти такое расстояние BD, при котором параметр t становится минимальным, т. е. найти наилучшее в данной ситуации решение – оптимальное.

Этап работы с компьютерной моделью:

Учитель: теперь на рабочий лист Excel разместим все необходимые данные и формулы, их связывающие. Образец внесения данных см. в приложении к заданию.

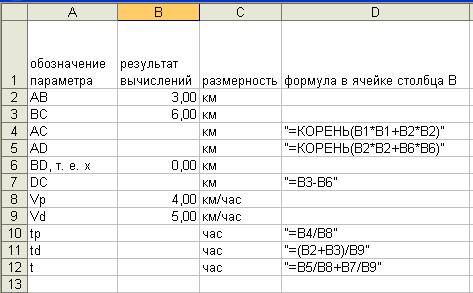
Учащиеся вводят обозначения, данные и формулы.

Учитель: Это и есть наша компьютерная модель. Можем ли мы быть уверенными, что модель полностью адекватна задаче? Как это проверить?

Ответы: для проверки адекватности можно ввести очень простые данные, чтобы даже в уме просчитать правильность результатов – предлагаем следующие значения:

AB=3, BC=4,  тогда AC должно стать равным 5. При х=0 AD=AB=3, а DC=4

Vp=1 и Vd=1, тогда будет tp = 5, td=t=7. Для единообразия результатов учитель на доске записывает предложенные данные. Подставим, получим:

	Учитель: совпал результат с ожидаемым? Можно ли считать, что мы все проверили? Ответ: этот совпал, но ведь х=0. Учитель:  ввиду ограниченности времени допустим, что этой проверки достаточно и наша модель адекватна задаче.

 

AB	3
BC	4
AC	5
AD	3
x	0
DC	4
vp	1
vd	1
tp	5
td	7
t	7

 

Теперь вводим все значения параметров в соответствии с постановкой задачи. Получаем:

 

 

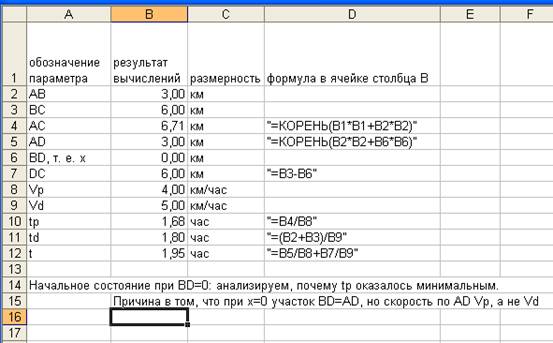
Итак, компьютерная модель разработана и даже получены первые результаты.

Теперь пытаемся минимизировать параметр t, изменяя параметр х.

Вызываем инструмент “поиск  решения” , устанавливаем режим поиска и добавляем ограничения.

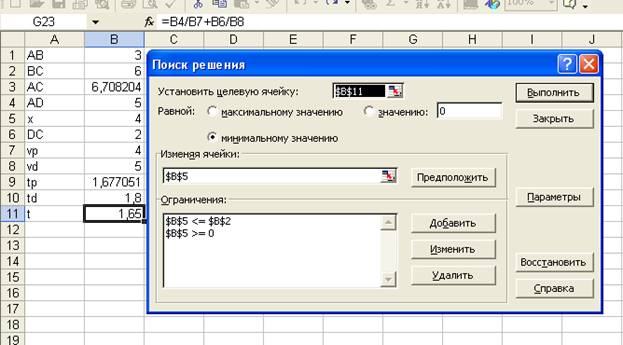
Очевидно, что полученный результат для tp грешит излишней точностью. Давайте отформатируем ячейки как числовые с точностью до 2х знаков. Когда надо было думать о форматировании ячеек?

Ответы: при внесении данных на лист Excel.

 

 

Полученный результат:

 

 

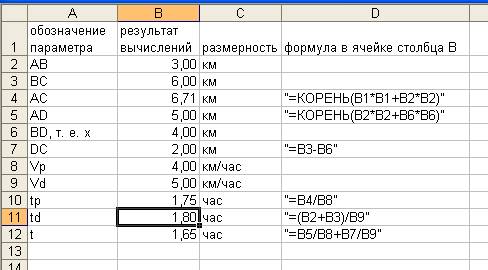
Обсуждение результата.

Учащиеся сообщают: при сравнении значений параметров видно, что сначала надо идти по полю, затем  выйти на дорогу в двух км от города.

По сравнению с движением напрямик мы выигрываем 0.1 часа, т. е. 6 мин.

Учитель предлагает провести компьютерный эксперимент, т. е. попробовать изменять расстояния и скорости, убрать ограничения на параметр х.

Результаты собраны в Приложении 3.

Учитель просит учащихся обобщить результаты работы.

Ответы: мы прошли через все этапы решения задачи с использованием компьютера – от возникновения самой идеи задачи, определения ее цели,  разработки модели через постановку задачи, перешли к компьютерной модели и проверили ее адекватность, затем получили решение с помощью такого инструмента электронных таблиц как “поиск решения”. Затем проводили различные изменения параметров задачи, т. е. компьютерный эксперимент, результаты получали очень быстро.

Учитель: вот и замечательно. А дома попробуйте записать математическую модель этой задачи, выразив параметр t как функцию х и исследуйте эту функцию.

 

Упражнения для глаз в соответствии с СанПиН (2 мин)

 

Самоанализ:

Урок основан на использовании проблемно-исследовательской технологии. Учащиеся показали хороший уровень владения техникой работы с электронными таблицами.

Вопросы моделирования изучались в 10-ом классе и мы неоднократно возвращались к ним в первом полугодии 11 класса. Результаты тестирования по теории хорошие. Правда, все же были ответы, что модель – это упрощенное представление…

 Урок прошел насыщенно, учащиеся активно работали с инструментами Excel, интересовались результатами соседей, даже соревновались, изменяя сами исходные данные ( как по скорости перемещения, так  расстояния). Для объективности скажу, что задачи оптимизации по экономике проще с точки зрения подбора параметров и выбранная мной задача о туристах привлекла меня возможностью графического построения и различных подходов к исследованию. Идея задачи позаимствована из книги :  В. В. Махрин «Учитесь работать на компьютере», М., ИНФРА-М, 2001.

При обсуждении звучали и критические замечания по отношению к реальности самой задачи, особенно насчет скорости перемещения по полю и т.п.