Дополнительный материал к рабочей программе элективного курса "Практикум по геометрии 9 класс"

Сумма углов треугольника. Внешние углы треугольника. Повторяем теорию.

Теорема.

Сумма углов треугольника равна 180⁰.

∠𝐴 + ∠𝐵 + ∠𝐶 = 180⁰

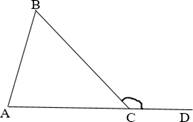Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.

∠𝐵𝐶𝐷 – внешний.

Свойство.

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

∠𝐵𝐶𝐷 = ∠𝐴 + ∠𝐵.

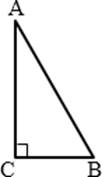Свойства прямоугольного треугольника.

1.            Сумма     двух     острых     углов    прямоугольного треугольника равна 90⁰.

∠𝐴 + ∠𝐵 = 90⁰

2.            Катет    прямоугольного   треугольника,   лежащий против угла в 30⁰, равен половине гипотенузы.

Если ∠𝐴 = 30⁰, то

𝐶𝐵 =

¹ 𝐴𝐵

2

3.            Если   катет   прямоугольного  треугольника  равен половине гипотенузы, то угол, лежащий против этого катета, равен 30⁰.

Если 𝐶𝐵 = 1 𝐴𝐵, то ∠𝐴 = 30⁰

2

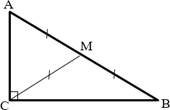
4.            Медиана     прямоугольного     треугольника,

проведенная к гипотенузе, равна половине гипотенузы.

Если CM – медиана, то

𝐶𝑀 =

¹ 𝐴𝐵.

2

Проверяем себя.

Т1. Выберите верные утверждения:

а) Внешний угол треугольника равен сумме двух внутренних углов. б) Смежные углы равны.

в) Вертикальные углы равны.

г) В тупоугольном треугольнике все углы тупые.

Ответ: в).

Т2. Выберите неверные утверждения:

а) Сумма смежных углов 180°.

б) Сумма углов треугольника 180°. в) Сумма вертикальных углов 180°.

г) Один из углов треугольника всегда не превышает 60 градусов. д) Внешний угол больше любого внутреннего угла треугольника Ответ: в), д).

Т3. Заполните пропуски:

а)    Внешний    угол    треугольника    равен                       

треугольника, не смежных с ним.

б) В остроугольном треугольнике              острые.

Ответ: а) сумме; б) все углы.

двух    углов

Решаем задачи

1.     а) В треугольнике два угла равны 26° и 63°. Найдите его третий угол. Ответ дайте в градусах.

Ответ: 91

б) Один из острых углов прямоугольного треугольника равен 34°. Найдите его другой острый угол. Ответ дайте в градусах.

Ответ:56

в) Один из острых углов прямоугольного треугольника равен 47°. В ответ запишите наименьший угол треугольника.

Ответ: 43

2.     а) В треугольнике АВС ∠B=15°, угол А в 2 раза больше. Найдите ∠С.

Ответ:135

б) В треугольнике АВС ∠B в 3 раза больше ∠А. Найдите ∠C, если ∠A=20°.

Ответ: 100.

в) В треугольнике АВС ∠А в 2 раза больше ∠B, ∠В=30°. Найдите ∠C.

Ответ: 90.

3. 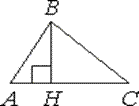            а) В остроугольном треугольнике ABC проведена высота BH, ∠BAC=46°. Найдите угол ABH. Ответ дайте в градусах.

Ответ: 44

б) В прямоугольном треугольнике ABC с прямым углом В проведена высота BH, ∠BAC=54°. Найдите угол HBС. Ответ дайте в градусах.

Ответ: 54

в) В остроугольном треугольнике ABC проведена высота BH, ∠BCA=50°.

Найдите угол HBС. Ответ дайте в градусах.

Ответ: 40

4.       а) В треугольнике ABC угол A равен 23°, угол B равен

240. Найдите внешний угол при вершине C. Ответ дайте в градусах.

Ответ: 47

б) В треугольнике ABC внешний угол при вершине C равен 124°. Найдите сумму углов А и В. Ответ дайте в градусах.

Ответ: 124

в) В треугольнике ABC внешний угол при вершине C равен 80°, угол A равен 44⁰. Найдите угол В. Ответ дайте в градусах.

Ответ: 36

5.     а) В треугольнике ABC известно, что AB = 5, BC = 10, угол A равен 90°. Найдите ∠B.

Ответ: 60

б) В треугольнике ABC известно, что AB = 17, BC = 34, угол A равен 90°.

Найдите ∠C.

Ответ: 30

в) В треугольнике ABC известно, что AC = 44, BC = 88, угол A равен 90°.

Найдите ∠C.

Ответ: 60

6. 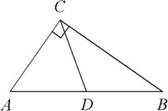          а) В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.

Ответ: 55

б) В треугольнике ABC CD — медиана, угол C равен 90°, угол А равен 56°. Найдите угол ADC. Ответ дайте в градусах.

Ответ: 68

в) В треугольнике ABC CD — медиана, угол C равен 90°, угол А равен 24°.

Найдите угол ВCD. Ответ дайте в градусах.

Ответ: 66

7. 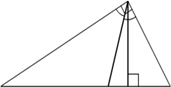           а) В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника.

Ответ дайте в градусах.

Ответ: 31

б) В прямоугольном треугольнике меньший угол равен 23⁰. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Ответ: 22

в) В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 8°. Найдите больший острый угол прямоугольного треугольника. Ответ дайте в градусах.

Ответ: 53

Задачи с развернутым ответом

1.            В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла равен 18⁰. Найдите больший острый угол данного треугольника. Ответ дайте в градусах.

Ответ: 54

2.            Сумма двух углов треугольника и внешнего угла к третьему равна 156⁰. Найдите этот третий угол. Ответ дайте в градусах.

Ответ: 102

3.             В остроугольном треугольнике DEF EH – высота, DM – биссектриса, O – точка пересечения прямых EH и DM, угол EDF равен 28⁰. Найдите угол DOE. Ответ дайте в градусах.

Ответ: 104