
В случае необходимости оказать учащимся поддержку в виде алгоритма решения задачи.
Задача 1.
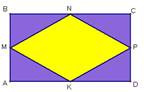
Середины сторон прямоугольника АВСD являются вершинами четырехугольника MNPK. Периметр прямоугольника равен 40 см, одна сторона в три раза больше другой. Из прямоугольника случайным образом выбирается точка. Найдите вероятность того, что она принадлежит четырехугольнику MNPK.
|
Алгоритм 1-1 |
|
|
1. |
Определите вид фигуры MNPK. |
|
2. |
Найдите стороны прямоугольника АВСD. |
|
3. |
Найдите площадь прямоугольника АВСD. |
|
4. |
Найдите площадь четырехугольника MNPK. |
|
5. |
Вычислите вероятность. |
Алгоритм 1-2
|
1. |
Определите вид фигуры MNPK. |
|
2. |
Найдите стороны
прямоугольника АВСD. |
|
3. |
Найдите площадь прямоугольника АВСD. |
|
4. |
Найдите площадь
четырехугольника MNPK. |
|
5. |
Вычислите
вероятность. |
|
6 |
Ответ: 0,5 |
Задача 2.
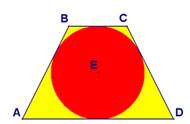
Стороны равнобедренной трапеции касаются окружности с центром в точке О. Основания трапеции равны 4 см и 16 см. Из трапеции случайным образом выбирается точка. Найдите вероятность того, что она не принадлежит кругу, ограниченному данной окружностью.
|
Алгоритм 2-1 |
|
|
1. |
Используя определение равнобедренной трапеции и свойство четырехугольника, описанного около окружности, найдите боковые стороны трапеции. |
|
2. |
Опустите высоты и рассмотрев получившиеся прямоугольные треугольники, найдите длину высоты трапеции. |
|
3. |
Найдите площадь трапеции. |
|
4. |
Найдите радиус окружности. |
|
5. |
Найдите площадь круга. |
|
6. |
Вычислите вероятность |
Алгоритм 2-2
|
1 а) Если четырехугольник описан около окружности, то суммы противоположных сторон равны. Используя это свойство, найдите сумму боковых сторон трапеции. б) Используйте определение равнобедренной трапеции и найдите каждую из боковых сторон. |
|
|
|
2. а) Опустите высоты, найдите длины отрезков, отсекаемых высотами. б) Рассмотрите один из получившихся прямоугольных треугольников и, используя теорему Пифагора, найдите высоту трапеции. |
|
|
|
Найдите
площадь трапеции по формуле |
|
|
|
|
|
|
|
5.
Найдите площадь круга по формуле |
|
|
|
6.
Вычислите вероятность попадания точки внутрь круга по формуле |
|
|
|
7. Найдите вероятность того, что она не принадлежит кругу. |
|
|
|
8.
Ответ: |
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.