Движение по траектории

 Движение по траектории

Движение по траектории реализуется аналогично выше рассмот- ренному примеру. Для реализации движения по прямой нужно увеличи- вать переменные, являющиеся узловыми точками, на определённые константы: в приведённом выше примере это переменные x2 и y2. Для задания более сложной траектории можно использовать различные па- раметрические кривые.

В случае движения на плоскости обычно изменению подвергается один параметр. Рассмотрим пример реализации движения окружности по декартову листу. Декартов лист – это плоская кривая третьего по-

рядка, удовлетворяющая уравнению в прямоугольной системе x³+y³=3·a·x·y. Параметр 3·a определяется как диагональ квадрата, сто- рона которого равна наибольшей хорде петли.

При переходе к параметрическому виду получаем:

,

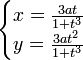где t=tg φ.

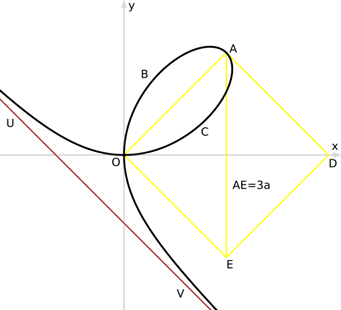Рис. 11.1. Декартов лист

Программная реализация выглядит следующим образом:

private int x1, y1, x2, y2; private double a, t, fi;

private Pen pen = new Pen(Color.DarkRed, 2);

private void Form1_Load(object sender, EventArgs e)

{

x1 = ClientSize.Width / 2; y1 = ClientSize.Height / 2; a = 150;

fi = -0.5;

t = Math.Tan(fi);

x2 = x1 + (int)((3 * a * t) / (1 + t * t * t));

y2 = y1 - (int)((3 * a * t * t) / (1 + t * t * t));

}

private void Form1_Paint(object sender, PaintEventArgs e)

{

Graphics g = e.Graphics; g.DrawEllipse(pen, x2, y2, 20, 20);

}

private void timer1_Tick(object sender, EventArgs e)

{

fi += 0.01;

t = Math.Tan(fi);

x2 = x1 + (int)((3 * a * t) / (1 + t * t * t));

y2 = y1 - (int)((3 * a * t * t) / (1 + t * t * t)); Invalidate();

}

² https://ru.wikipedia.org/wiki/Циклоидальная_кривая