
7.1. Определение Р-матрицы и псевдоплана КЗЛП
Рассмотрим задачу
![]() (7.1)
(7.1)
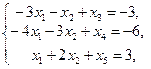 (7.2)
(7.2)
![]() ,
, ![]() .
(7.3)
.
(7.3)
Рассмотрим расширенную матрицу системы линейных уравнений (7.2):
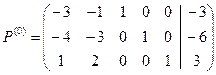
Матрица ![]() содержит
единичную подматрицу порядка 3 и, следовательно, определяет базисное решение
содержит
единичную подматрицу порядка 3 и, следовательно, определяет базисное решение
![]() ,
, ![]() .
.
системы уравнений, причем ![]() .
.
Так как элементы (n + 1 = 6)-го столбца матрицы системы ![]() не
являются неотрицательными, то она не является К-матрицей ЗЛП.
Вычислим симплекс-разности матрицы
не
являются неотрицательными, то она не является К-матрицей ЗЛП.
Вычислим симплекс-разности матрицы ![]() :
:
![]() ,
, ![]() .
.
Так как все
симплекс-разности матрицы ![]() являются неотрицательными, то
базисное решение
являются неотрицательными, то
базисное решение ![]() не являющееся допустимым решением
ЗЛП, является «лучшим», чем оптимальное решение.
не являющееся допустимым решением
ЗЛП, является «лучшим», чем оптимальное решение.
При решении задачи симплекс-методом текущее базисное решение является допустимым, но неоптимальным. Эти соображения позволяют построить метод решения определенного класса ЗЛП. В этом методе, называемом двойственным симплекс-методом, на каждой итерации обеспечивается выполнение условия оптимальности текущего базисного решения, не являющегося допустимым. Критерием окончания процесса итераций является получение допустимого решения.
Определение 7.1. Р-матрицей КЗЛП
![]() (7.4)
(7.4)
![]() ,
(7.5)
,
(7.5)
![]() ,
, ![]() .
(7.6)
.
(7.6)
будем называть расширенную матрицу системы линейных уравнений, содержащую единичную подматрицу порядка m на месте n первых столбцов, все симплекс-разности которой неотрицательны.
Очевидно, что всякая Р-матрица ЗЛП определяет некоторое базисное решение системы уравнений (7.5) (см. пример (7.1) – (7.3))
Определение 7.2. Базисное решение системы линейных уравнений (7.5), определяемое Р-матрицей, называется псевдопланом ЗЛП.
7.2. Условия перехода от одной Р-матрицы к другой
Пусть известна Р-матрица ![]() ЗЛП
(7.4) – (7.6), определяющая псевдоплан
ЗЛП
(7.4) – (7.6), определяющая псевдоплан ![]() ,
,
![]() .
.
Условия перехода от
матрицы ![]() к матрице
к матрице ![]() составляют содержание теоремы 7.1.
составляют содержание теоремы 7.1.
Теорема 7.1. Пусть ![]() и
в l -й строке матрицы
и
в l -й строке матрицы ![]() есть
хотя бы один отрицательный элемент. Тогда с помощью одного шага метода
Жордана-Гаусса можно построить новую Р-матрицу
есть
хотя бы один отрицательный элемент. Тогда с помощью одного шага метода
Жордана-Гаусса можно построить новую Р-матрицу ![]() , выбрав направляющий элемент из
условия
, выбрав направляющий элемент из
условия
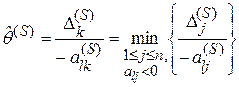 . (7.7)
. (7.7)
Замечание 1. Если в матрице ![]() нет
нет
![]() ,
то определяемый ею псевдоплан является решением ЗЛП.
,
то определяемый ею псевдоплан является решением ЗЛП.
Теорема 7.2. Пусть ![]() и
в l -й строке матрицы
и
в l -й строке матрицы ![]() нет
ни одного отрицательного элемента. Тогда множество планов Р ЗЛП (7.4)
– (7.6) пусто.
нет
ни одного отрицательного элемента. Тогда множество планов Р ЗЛП (7.4)
– (7.6) пусто.
Замечание 2. При переходе от матрицы ![]() к
матрице
к
матрице ![]() целевая функция изменяется в соответствии с формулой,
аналогичной выражению (5.6)
целевая функция изменяется в соответствии с формулой,
аналогичной выражению (5.6)
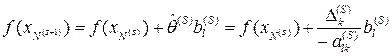 , (7.8)
, (7.8)
откуда следует, что
![]() ,
(7.9)
,
(7.9)
так как ![]() и
и
![]() .
Из неравенства (7.8) следует, что при переходе от одного псевдоплана к другому
значению целевой функции
.
Из неравенства (7.8) следует, что при переходе от одного псевдоплана к другому
значению целевой функции ![]() не возрастает.
не возрастает.
7.3. Алгоритм Р-метода
Будем считать, что известна исходная Р-матрица ![]() ЗЛП (7.4) – (7.6), определяющая
исходный псевдоплан
ЗЛП (7.4) – (7.6), определяющая
исходный псевдоплан ![]() ,
, ![]() .
.
В Р-методе
последовательно строят Р-матрицы ![]() ,
,![]() ,…,
,…,![]() , … задачи линейного
программирования, пока не получат Р-матрицу ЗЛП, определяющую ее
оптимальный план.
, … задачи линейного
программирования, пока не получат Р-матрицу ЗЛП, определяющую ее
оптимальный план.
Рассмотрим алгоритм на S-й итерации метода. В начале S-й итерации имеем Р-матрицу
![]() ЗЛП,
определяющую псевдоплан
ЗЛП,
определяющую псевдоплан
![]() ,
, ![]() .
.
Шаг 1. Найдем номер строки l из условия
![]() , (7.10)
, (7.10)
Шаг 2. Если ![]() ,
то псевдоплан
,
то псевдоплан
![]() ,
, ![]() .
.
является оптимальным опорным планом, а
![]() , (7.11)
, (7.11)
есть оптимальное значение целевой
функции ![]() , иначе переходим к шагу 3.
, иначе переходим к шагу 3.
Шаг 3. Если ![]() ,
,
![]() ,
то задача линейного программирования не имеет решения (множество планов Р
пусто), иначе переходим к шагу 4.
,
то задача линейного программирования не имеет решения (множество планов Р
пусто), иначе переходим к шагу 4.
Шаг 4. Вычисляем для столбцов ![]() матрицы
матрицы
![]() (
(![]() ,
,
![]() )
симплекс-разности
)
симплекс-разности ![]() и находим номер
и находим номер ![]() из
условия вида (7.7)
из
условия вида (7.7)
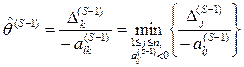 . (7.12)
. (7.12)
Направляющий элемент на S-й итерации метода есть элемент ![]() .
.
Шаг 5. Вычисляем компоненты вектора ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Шаг 6. Производим один шаг метода
Жордана-Гаусса с направляющим элементом ![]() . Вычисляем элементы Р-матрицы
. Вычисляем элементы Р-матрицы
![]() методом
Жордана-Гаусса. Присваиваем переменной алгоритма S следующее значение и переходим к шагу 1.
методом
Жордана-Гаусса. Присваиваем переменной алгоритма S следующее значение и переходим к шагу 1.
7.4. Примеры решения задач Р-методом
Пример 7.1. Решим задачу (7.1) - (7.3), рассмотренную в п.7.1:
![]() ,
,
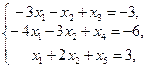
![]() ,
, ![]() .
.
Результаты решения приведены в симплекс-таблице (см. табл. 7.1)
Так как компоненты
псевдоплана ![]() являются неотрицательными, то
являются неотрицательными, то ![]() является
оптимальным опорным планом ЗЛП (7.1) - (7.3). Отметим, что все
симплекс-разности остались неотрицательными. Итак,
является
оптимальным опорным планом ЗЛП (7.1) - (7.3). Отметим, что все
симплекс-разности остались неотрицательными. Итак,
![]() и
и ![]() .
.
Таблица 7.1
|
S |
i |
|
|
|
-2 |
-4 |
0 |
0 |
0 |
k, l |
|
|
1 |
2 |
3 |
4 |
5 |
|||||
|
|
|
|
|
|
|
|||||
|
|
1 2 3 |
3 4 5 |
0 0 0 |
-3 -6 3 |
-3 -4 1 |
-1 -3 2 |
1 0 0 |
0 1 0 |
0 0 1 |
|
|
|
|
2 |
4 |
0 |
0 |
0 |
k=1 l=2 |
|||
|
|
2/4 |
4/3 |
|
|
|
|||||
|
1
|
1 2 3 |
3 1 5 |
0 -2 0 |
3/2 3/2 3/2 |
0 1 0 |
5/4 3/4 5/4 |
1 0 0 |
3/4 -1/4 1/4 |
0 0 1 |
|
|
|
|
0 |
5/2 |
0 |
1/2 |
0 |
|
|||
|
|
|
|
|
|
|
|||||
Пример 7.2. Решить задачу
![]() ,
(7.13)
,
(7.13)
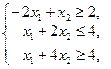 (7.14)
(7.14)
![]() ,
, ![]() .
(7.15)
.
(7.15)
Приведем рассматриваемую ЗЛП к каноническому виду, для этого преобразуем (7.14)
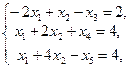
и далее окончательно имеем
![]() ,
(7.16)
,
(7.16)
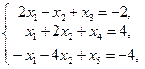 (7.17)
(7.17)
![]() ,
, ![]() .
(7.18)
.
(7.18)
Расширенная матрица системы линейных уравнений (7.17) не является Р-матрицей рассматриваемой ЗЛП, так как
![]() =(0,
0, 0)
=(0,
0, 0) ![]() + 1 = 1 >
0 ,
+ 1 = 1 >
0 , ![]() =(0,
0, 0)
=(0,
0, 0) ![]() - 2 = -2 < 0.
- 2 = -2 < 0.
Следовательно, к решению ЗЛП (7.13) – (7.15) Р-метод не применим.
Пример 7.3. Решить задачу
![]() ,
(7.19)
,
(7.19)
![]() (7.20)
(7.20)
![]() ,
, ![]() .
(7.21)
.
(7.21)
Приведем рассматриваемую ЗЛП к каноническому виду. Получим
![]() ,
(7.22)
,
(7.22)
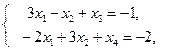 (7.23)
(7.23)
![]() ,
, ![]() .
(7.24)
.
(7.24)
Так как расширенная матрица
![]() =
= ![]()
системы линейных уравнений
рассматриваемой задачи является Р-матрицей (![]() =
6 >0;
=
6 >0; ![]() = 3 >0 ), то задачу можно решить Р -
методом. Решение задачи приведено в симплексной таблице (см. табл. 7.2).
= 3 >0 ), то задачу можно решить Р -
методом. Решение задачи приведено в симплексной таблице (см. табл. 7.2).
Так как ![]() =
-4 < 0, а все
=
-4 < 0, а все ![]() 0, то множество планов ЗЛП (7.19) –
(7.21) является пустым множеством.
0, то множество планов ЗЛП (7.19) –
(7.21) является пустым множеством.
Таблица 7.2
|
S |
i |
|
|
|
-6 |
-3 |
0 |
0 |
k, l |
|
|
1 |
2 |
3 |
4 |
|||||
|
|
|
|
|
|
|||||
|
|
1 2 |
3 4 |
0 0 |
-1 -2 |
3 -2 |
-1 3 |
1 0 |
0 1 |
|
|
|
|
6 |
3 |
0 |
0 |
k=1 l=2 |
|||
|
|
6/2 |
|
|
|
|||||
|
1
|
1 2 |
3 1 |
0 -6 |
-4 1 |
0 1 |
7/2 -3/2 |
1 0 |
3/2 -1/2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
7.5. Задача и упражнения
7.5.1. Решить следующие задачи Р-методом.
Предприятию необходимо выпустить по плану продукции А1 - 500 единиц, А2 - 300, А3 - 450. Каждый вид изделия может производиться на двух машинах. Как распределить работу машин, чтобы общие затраты времени на выполнение плана были минимальными, если задана матрица затрат. Ресурс времени каждой машины приведен справа от таблицы. Записать модель исследуемой операции в форме, допускающей использование Р-метода.
1. ![]() 2.
2.
![]() 3.
3. ![]()
4. ![]() 5.
5. ![]() 6.
6. ![]()
7. ![]() 8.
8. ![]() 9.
9. ![]()
10. ![]() 11.
11. ![]() 12.
12. ![]()
13. ![]() 14.
14. ![]() 15.
15. ![]()
16. ![]() 17.
17. ![]() 18.
18. ![]()
19. ![]() 20.
20. ![]()
7.5.2. Решить задачи из п. 7.5.1 Р-методом в случае, если предприятию необходимо выпустить по плану продукции А1 - 400 единиц, А2 - 400, А3 - 400.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.