Элементы векторной алгебры

·  ·  Элементы векторной алгебры

Отрезок, имеющий определенную длину и определенное направление, называется вектором. Вектор служит для геометрического изображения физической векторной величины.

Два вектора называются равными, если выполнены следующие три условия:

1. длины векторов равны

2. векторы коллинеарны, т.е. расположены на одной прямой или параллельных прямых

3. векторы направлены в одну сторону.

Из определения равенства векторов следует, что при параллельном переносе вектора получается вектор, равный исходному.

Над векторами определены следующие простейшие операции: сложение, вычитание и умножение вектора на число. Эти операции непосредственно связаны с соответствующими операциями над векторными величинами в механике.

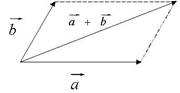Рис.1

Суммой двух векторов и называется вектор , выходящий из их общего начала, который по величине и направлению изображается диагональю параллелограмма, построенного на векторах и . (правило параллелограмма) (рис. 1).

Наряду с правилом параллелограмма используется равносильное ему правило треугольника: суммой векторов и называется вектор, который выходит из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (рис. 2).

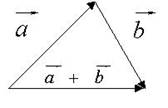
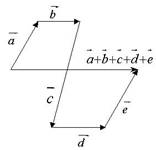
Рис.2                                      Рис.3

Сложение нескольких векторов производится при помощи последовательного применения правила треугольника.

На рис. 3 представлено построение суммы пяти векторов: , , , и .

Разностью двух векторов и называется вектор, который в сумме с вектором дает вектор . Если вектора и приведены к общему началу, то разность есть вектор, идущий из конца вектора к концу вектора (рис. 4).

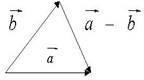
Рис.4

При умножении вектора на число l длина вектора умножается на , направление сохраняется при l >0 и заменяется противоположным при l <0.

Операции сложения векторов и умножения векторов на число подчиняются законам:

1. закон переместительности (коммутативный): , т.е. сумма не зависит от порядка слагаемых

2. закон сочетательности (ассоциативный): , т.е. чтобы прибавить сумму, можно прибавить последовательно каждое слагаемое

3. распределительный (дистрибутивный) закон: .

Отметим еще, что из определения умножения вектора на число вытекает справедливость равенств:

где l ₁ и l ₂ – числа.

Проекцией вектора на ось (направленная прямая) называется произведение длины вектора на косинус угла между ними:

Проекция суммы векторов на любую ось равна сумме проекций слагаемых векторов на эту ось:

Вектор , представленный в виде

,

где , ,…, - различные векторы, a, b,…, g - числа, называется линейной комбинацией векторов , ,…, .

Векторы , ,…, называются линейно зависимыми, если существуют такие числа a , b,…, g , не все равные нулю, что имеет место равенство

Если же таких чисел a, b,…, g нет, то векторы , ,…, называются линейно независимыми.

Заметим, два вектора линейно зависимы тогда и только тогда, когда они коллинеарны; три вектора линейно зависимы тогда и только тогда, когда они компланарны (параллельны одной и той же плоскости); четыре вектора (и более) всегда линейно зависимы.

Следовательно, наибольшее число линейно независимых векторов в пространстве равно трем, на плоскости таких векторов два, а на прямой линии – один.

Совокупность линейно независимых векторов, через которые линейно выражается любой вектор пространства, называется базисом этого пространства. Векторы, составляющие базис пространства, называются базисными.

Наибольшее число линейно независимых векторов пространства называется размерностью этого пространства.

В соответствии с этим прямую линию обычно называют одномерным пространством, плоскость является двумерным пространством, а обычное пространство – трехмерным.

Рассмотрим прямоугольную систему координат и зададим произвольную точку М трехмерного пространства (рис. 5).

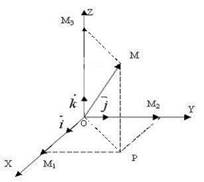
Рис.5

Вектор является радиус-вектором точки М. Из точки М проведем прямую, параллельную оси OZ, до пересечения в точке Р с плоскостью XOY и из точки Р проведем прямую параллельно оси OY до пересечения в точке М₁ с осью ОХ. Очевидно, будем иметь

.

Откладывая векторы и от точки 0, заменяя их равными им векторами

будем иметь

(1.10)

Это равенство показывает, что всякий вектор можно разложить на три слагаемых вектора, лежащих на осях координат. Векторы , и называются компонентами или составляющими данного вектора .

От точки 0 – начала координат в положительном направлении каждой оси координат отложим по вектору длины, равной единице. Обозначим три введенных попарно взаимно ортогональных единичных вектора соответственно через , , и назовем их основными векторами. Вектор , как и вектор , расположен на оси абсцисс, а поэтому имеем

где х есть число, являющееся проекцией вектора на ось абсцисс. Аналогично имеем

где y,z – проекции вектора соответственно на оси ординат и аппликат. Таким образом, равенство (1.10) перепишется в виде

(1.11)

Значение равенства (1.11) в теории векторов исключительно большое. При помощи этого равенства устанавливается связь между геометрической и алгебраической частями теории векторов. Взаимно дополняя друг друга, они создают то, чем так выгодно отличается векторная алгебра: геометрическая теория дает возможность широко использовать геометрические представления, алгебраическая часть позволяет производить все выкладки.

Вместо полной записи (1.11) часто пользуются сокращенной

Применяя предложение о том, что проекция суммы векторов на любую ось равна сумме проекций этих векторов относительно каждой оси координат, мы заключаем: при сложении векторов одноименные проекции их складываются. Запишем это так, если

то

Из правила сложения векторов вытекает правило вычитания векторов: чтобы вычесть вектор, нужно вычесть его проекции, т.е.

Аналогично, чтобы умножить вектор на число, нужно умножить все его проекции на это число.

Пример 10. Найти координаты вектора , если и .

Решение: вектор (рис. 6) равен разности между векторами и , т.е. . Так как векторы и являются радиус-векторами точек А и В соответственно, а координаты радиус-вектора точки равны соответственно координатам самой точки, то , .

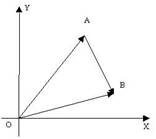
·  ·  Рис.6

Далее, применяя правило вычитания векторов, заданных своими координатами (проекциями), получим:

Отсюда следует правило: для того, чтобы найти координаты вектора, зная координаты его начальной и конечной точек, нужно из координат конечной точки вычесть соответствующие координаты начальной точки.

Пример 11. Найти координаты точки М, делящей отрезок AB в отношении l , если и .

Решение: очевидно, что . Обозначим через x, y, z координаты точки М, тогда

Далее, применяя правило умножения вектора на число и условия равенства двух векторов, заданных в координатной форме, получим:

Отсюда следует

 

·  ·  Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению их длин (модулей), умноженному на косинус угла между ними.

Скалярное произведение принято обозначать одним из трех способов:

Согласно определению имеем

Заметив, что есть проекция вектора на направление вектора , мы можем записать

Аналогично

Таким образом, скалярное произведение двух векторов равно длине одного из них, умноженной на проекцию другого вектора на первый.

Основными свойствами скалярного произведения являются следующие:

1. скалярное произведение обращается в нуль в том и только в том случае, когда векторы перпендикулярны.

2. скалярное произведение обладает свойством переместительности

3. исключительно важное значение имеет распределительный закон.

Его применение столь же велико как в арифметике, так и в алгебре. Этот закон формулируется так: для любых трех векторов , , справедливо равенство

4. скалярное произведение обладает свойством сочетательности относительно числового множителя:

Если векторы и заданы своими координатами

, , то

(1.13)

или скалярное произведение векторов равно сумме произведений одноименных проекций.

Применяя формулу 1.13 при , найдем:

С другой стороны, согласно определению скалярного произведения, получим

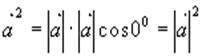
Следовательно, мы имеем следующую формулу для определения длины вектора:

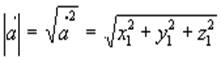(1.14)

т.е. длина вектора равна корню квадратному из скалярного квадрата вектора или из суммы квадратов его проекций.

Согласно определению скалярного произведения векторов, имеем

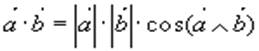
Из этой формулы получаем:

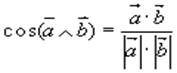
т.е. косинус угла между векторами равен их скалярному произведению, деленному на произведение их модулей.

Применяя формулы 1.13 и 1.14, получим:

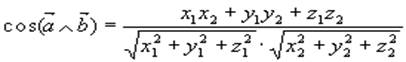(1.15)

 

·  ·  Векторное произведение векторов

Векторным произведением вектора на вектор называется третий вектор , удовлетворяющий следующим трем условиям:

1. длина вектора равна площади параллелограмма, построенного на векторах и , т.е.

2. вектор ортогонален векторам и

3. вектор направлен так, что кратчайший поворот от вектора к вектору представлялся происходящим против часовой стрелки, если смотреть из конца вектора (рис. 7).

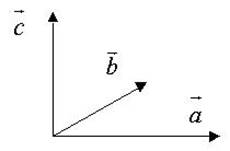
·  ·  ·  ·  Рис.7

Векторное произведение вектора на вектор обозначается одним из двух способов: или .

Векторное произведение векторов обладает следующими свойствами:

1. при перестановке сомножителей знак векторного произведения изменяется на противоположный, т.е.

2. векторное произведение обладает свойством сочетательности относительно числового множителя, т.е.

3. векторное произведение подчиняется распределительному закону, т.е.

Если векторы и заданы своими координатами и , то можно записать в символической, легко запоминаемой форме, если воспользоваться понятием определителя третьего порядка:

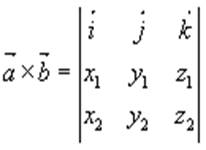(1.16)

Пример 12. Найти площадь треугольника ABC с вершинами в точках , и .

Решение: так как вектор имеет координаты , а вектор , то

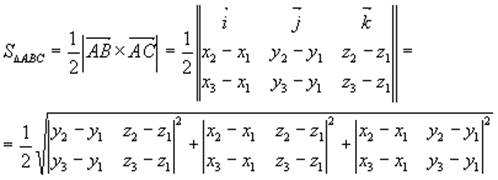
Если треугольник ABC лежит в плоскости XOY, то z₁=z₂=z₃=0 и тогда

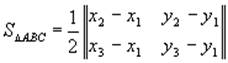(1.17)

 

·  ·  Смешанное произведение векторов

Выясним, что можно сказать о произведении трех векторов. Если мы умножим скалярно вектор на , то получим число (скаляр). При умножении этого числа на третий вектор , получим вектор, коллинеарный вектору .

Совсем иное будет дело, если вектор умножим векторно на вектор , в результате получим новый вектор . Представляется интересным исследовать произведения, как скалярное, так и векторное, этого вектора на вектор . В первом случае будем иметь векторно-скалярное произведение , а во втором случае – двойное векторное произведение . Векторно-скалярное произведение называется также смешанным произведением и обозначается или . Уясним геометрический смысл смешанного произведения векторов , , .

 

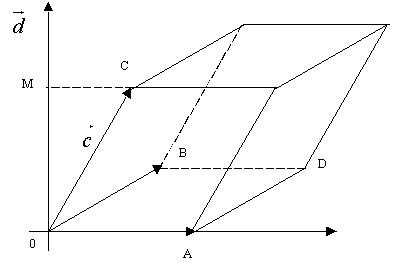
·  ·  ·  ·  ·  ·  Рис.8

Пусть рассматриваемые векторы , , некомпланарны. Векторное произведение есть вектор, по длине численно равный площади параллелограмма OADB, построенного на векторах и , и направленный перпендикулярно к плоскости параллелограмма (рис. 8). Скалярное произведение . Проекция вектора на вектор перпендикулярна к плоскости параллелограмма OADB, равна расстоянию точки С (конец вектора ) от плоскости этого параллелограмма, взятому со знаком + или -.

Построим параллелепипед на векторах , , как на ребрах. Высота этого параллелепипеда есть абсолютная величина проекции вектора , а площадь основания (параллелограмма OADB) численно равна длине вектора .

Итак, смешанное произведение по абсолютной величине равно объему параллелепипеда, построенного на векторах-сомножителях, как на ребрах.

Смешанное произведение ненулевых векторов равно нулю тогда и только тогда, когда векторы компланарны; иначе говоря, равенство есть необходимое и достаточное условие компланарности векторов , , .

Если векторы , , заданы своими проекциями , , , то смешанное произведение определяется формулой

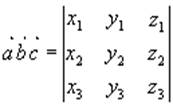(1.18)

Напомним, что объем параллелепипеда, построенного на векторах , , , и, следовательно, объем образованной ими пирамиды находятся соответственно по формулам:

;