
Эллипсометрия является высокочувствительным методом, который основан на регистрации изменения состояния поляризации света в результате его взаимодействия с исследуемой поверхностью. Этот метод позволяет производить измерение толщин и оптических параметров тонкоплёночных покрытий, как в целом, так и их отдельно взятых слоев. При этом эллипсометрия является практически единственным оптическим методом, позволяющим уверенно определять толщины пленок менее половины длины волны зондирующего излучения. Так же эллипсометрия позволяет контролировать однородность покрытий по толщине и площади. Она эффективна при исследовании как прозрачных, так и поглощающих структур.
Проведение эллипсометрических измерений возможно как в проходящем, так и в отраженном свете. В первом случае говорят о просвечивающей эллипсометрии, а во втором – об отражательной. Зачастую они удачно дополняют друг друга, но, по ряду причин, именно отражательная эллипсометрия получила широкое практическое распространение. Эллипсометрические измерения в проходящем свете возможны только для оптически прозрачных образцов, причем таких, объем которых не влияет на поляризационные характеристики светового луча. Важным преимуществом отражательной эллипсометрии является то, что отраженная волна формируется в тонком приповерхностном слое исследуемого образца. Таким образом, исследование образцов именно в отраженном свете, позволяет получить ценную информацию о свойствах приповерхностного слоя вещества.
При отражении света от
поверхности параметры эллипса поляризации меняются [7]. Это изменение
характеризуется эллипсометрическими углами ![]() и
и ![]() :
:
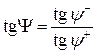 , (2.19)
, (2.19)
![]() . (2.20)
. (2.20)
Здесь верхний индекс «+» соответствует падающей волне, а «-» – отражённой.
Эллипсометрические углы связаны с
параметрами отражающей поверхности через обобщённые амплитудные коэффициенты
Френеля ![]() ,
, ![]() для p- и s-поляризации,
соответственно:
для p- и s-поляризации,
соответственно:
![]() . (2.21)
. (2.21)
Данное выражение называется основным уравнением эллипсометрии.
Задача о нахождении изменения параметров эллипса поляризации при взаимодействии поляризованного света с поверхностью называется прямой задачей эллипсометрии. Для её решения необходимо знание всех оптических и геометрических свойств поверхности и обрамляющих сред.
Аналитическое решение этой задачи для системы плоскопараллельных однородных изотропных сред имеет вид:
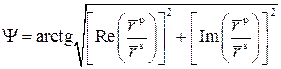 (2.22)
(2.22)
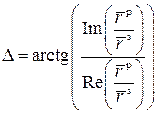 (2.23)
(2.23)
В полученных выражениях
значения коэффициентов отражения ![]() ,
, ![]() находятся из матрицы
рассеянья (2.5) по формуле (2.6) и определяются параметрами отражающей системы.
находятся из матрицы
рассеянья (2.5) по формуле (2.6) и определяются параметрами отражающей системы.
Следует обратить внимание, на то, что областью значений функции arctg(x) является интервал [-π/2; π/2], а Δ принадлежит интервалу [0; 2π]. Чтобы перейти в этот интервал значений Δ, нужно воспользоваться следующими правилами:
1.
если
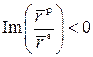 , а
, а 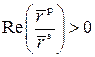 , то ∆ = ∆ +
2π;
, то ∆ = ∆ +
2π;
2.
если
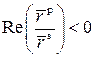 , то ∆ = ∆ +
π;
, то ∆ = ∆ +
π;
3.
в
остальных случаях (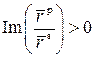 ,
,
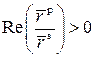 ) – ∆ = ∆.
) – ∆ = ∆.
Слои с плавным изменением оптических характеристик моделируются как совокупность плоскопараллельных однородных слоёв оптические характеристики каждого из которых задаются в соответствии с законом их изменения в моделируемом слое [188]. При этом, количество и толщины однородных слоёв выбираются исходя из толщины моделируемого слоя и требуемой точности вычислений. Для шероховатых слоёв предварительно, основываясь на геометрических и оптических свойствах элементов слоя, вводятся эффективные оптические характеристики и закон их изменения в слое [7]. В дальнейшем для таких слоёв используется та же модель, что и для слоёв с плавным изменением оптических характеристик.
Суть обратной задачи эллипсометрии (ОЗЭ) сводится к восстановлению одного или нескольких параметров, описывающих оптическую систему, по известному изменению ЭП, с использованием известных параметров системы. Ее решение в общем случае связано со значительными трудностями, так как она относится к математическому классу так называемых некорректно поставленных задач [189, 190]. Однако учет специфики исследуемых объектов и способа измерений позволяет существенно упростить этот процесс. Поэтому, существует большое число методов решения ОЗЭ, обусловленное множеством различных моделей поверхности и методов проведения эллипсометрических измерений. Так, в частности, для определения показателя преломления чистой изотропной подложки эллипсометрическим методом используется формула
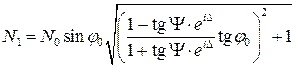 , (2.24)
, (2.24)
которая является аналитическим решением основного уравнения эллипсометрии в модели чистой поверхности [184].
Но реальные поверхности практически никогда не могут быть описаны моделью математически резкой границы раздела двух полубесконечных сред, для которой и справедливо выражение (2.24). Поэтому гораздо больший практический интерес представляют эллипсометрические исследования одно- и многослойных покрытий, а также естественных переходных (окисных, нарушенных, и пр.) слоёв существующих на поверхностях массивных материалов.
Многие
методы решения обратной задачи для тонкоплёночных покрытий основывается на
построении номограмм. При этом, как правило, предполагается, что показатель
преломления подложки известен. Одним из таких методов, является Малина-Ведама
[7]. Он предназначен для определения показателей преломления ![]() и поглощения
и поглощения ![]() , а также толщины
, а также толщины ![]() однослойных прозрачных
покрытий, нанесенных на подложку с известным показателем преломления, в рамках
так называемой однослойной модели. Эта модель является простейшей моделью однослойного
покрытия и описывает его как тонкий плоскопараллельный слой однородного
изотропного материала, разделяющего два однородных изотропных полупространства
из материалов с иными оптическими свойствами.
однослойных прозрачных
покрытий, нанесенных на подложку с известным показателем преломления, в рамках
так называемой однослойной модели. Эта модель является простейшей моделью однослойного
покрытия и описывает его как тонкий плоскопараллельный слой однородного
изотропного материала, разделяющего два однородных изотропных полупространства
из материалов с иными оптическими свойствами.
Так
как в рассматриваемом случае число неизвестных (![]() ,
, ![]() ,
, ![]() ) превышает число величин
) превышает число величин ![]() ,
, ![]() , получаемых в результате
одного измерения, метод требует выполнения, по крайней мере, двух измерений
эллипсометрических углов в различных условиях – либо при различных углах
падения, либо в различных иммерсионных средах. Тогда каждому измерению
соответствуют эллипсометрические углы
, получаемых в результате
одного измерения, метод требует выполнения, по крайней мере, двух измерений
эллипсометрических углов в различных условиях – либо при различных углах
падения, либо в различных иммерсионных средах. Тогда каждому измерению
соответствуют эллипсометрические углы ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т.д.
и т.д.
Уравнение
(2.21) для однослойной модели можно рассматривать как квадратное относительно
неизвестного фазового множителя ![]() :
:
![]() , (2.25)
, (2.25)
где
![]() ,
,
![]() ,
,
![]() .
.
Уравнение
(2.25) решается на множестве предполагаемых значений ![]() и
и ![]() для соответствующих
для соответствующих ![]() и
и ![]() . Из двух корней
уравнения (2.25) сначала следует выбрать те, которые имеют положительную
действительную и отрицательную мнимую части, а из них, в свою очередь только
те, для которых мнимая часть значения толщины плёнки вычисленная по формуле
. Из двух корней
уравнения (2.25) сначала следует выбрать те, которые имеют положительную
действительную и отрицательную мнимую части, а из них, в свою очередь только
те, для которых мнимая часть значения толщины плёнки вычисленная по формуле
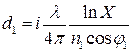 , (2.26)
, (2.26)
равна нулю. Пары
предполагаемых значений ![]() и
и
![]() , обеспечивающие выполнение
этих условий представляются в виде кривых, образованных совокупностью точек на
диаграмме в координатах
, обеспечивающие выполнение
этих условий представляются в виде кривых, образованных совокупностью точек на
диаграмме в координатах ![]() (Рис. 2.3). Точке пересечения кривых,
соответствующих различным условиям эксперимента соответствует искомое решение,
т.е. истинные значения
(Рис. 2.3). Точке пересечения кривых,
соответствующих различным условиям эксперимента соответствует искомое решение,
т.е. истинные значения ![]() ,
,
![]() ,
, ![]() .
.
Поиск решения обратной задачи эллипсометрии можно также представить как процесс минимизации некоторой функции в многомерном параметрическом пространстве, где в роли независимых переменных выступают величины, подлежащие определению [7]. Такой подход к решению обратной задачи эллипсометрии легко применить не только для однослойной модели поверхности, но и для модели с произвольным количеством слоёв.
При
наличии ![]() пар эллипсометрических
углов
пар эллипсометрических
углов ![]() ,
, ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() , полученных при
различных условиях проведения эксперимента, варьируя параметры исследуемой
системы
, полученных при
различных условиях проведения эксперимента, варьируя параметры исследуемой
системы ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() , в рамках выбранной
модели поверхности, возможно вычислить
, в рамках выбранной
модели поверхности, возможно вычислить ![]() пар эллипсометрических
углов
пар эллипсометрических
углов ![]() ,
, ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() ,
, ![]() , соответствующих этим
условиям измерения. Очевидно, что при верном подборе параметров системы функция
, соответствующих этим
условиям измерения. Очевидно, что при верном подборе параметров системы функция
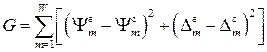 (2.27)
(2.27)
будет равна нулю или, по
крайней мере, минимальна. Таким образом, решение обратной задачи эллипсометрии
в общем случае сводится к поиску минимума указанной функции. Функция ![]() называется целевой
функцией или функцией ошибки.
называется целевой
функцией или функцией ошибки.
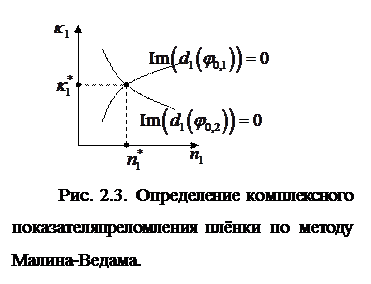 Следует
отметить, что выбор целевой функции при решении обратной задачи неоднозначен и
производится из соображений удобства и простоты вычислений. Также она должна
иметь глобальный минимум при условии равенства значений Ψ и ∆
вычисленных в рамках предполагаемых параметров модели измеренным экспериментально.
Следует
отметить, что выбор целевой функции при решении обратной задачи неоднозначен и
производится из соображений удобства и простоты вычислений. Также она должна
иметь глобальный минимум при условии равенства значений Ψ и ∆
вычисленных в рамках предполагаемых параметров модели измеренным экспериментально.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.