
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ
по дисциплине
ЕН.02 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
|
Специальность |
09.02.01 Компьютерные системы и комплексы |
|
Квалификация |
Техник по компьютерным системам |
|
Форма обучения |
очная |
|
Год набора |
2019 |
Составитель: Перетолчина Ю.Н., преподаватель
2019 г
Содержание
|
1.Паспорт фонда оценочных средств |
4 |
|
2.Контрольно-оценочные средства текущего контроля |
10 |
|
3.Контрольно-оценочные средства промежуточной аттестации |
10 |
|
4.Информационное обеспечение обучения |
11 |
|
Приложение А Контрольно-измерительный материал текущего контроля по дисциплине |
12 |
|
Приложение В Перечень вопросов для подготовки к экзамену |
26 |
|
Приложение С Типовые задания для подготовки к экзамену |
27 |
|
Приложение D Контрольно-измерительные материалы промежуточной аттестации |
30 |
1 Паспорт фонда оценочных средств
по учебной дисциплине ЕН.02 Теория вероятностей и математическая статистика по специальности 09.02.01 «Компьютерные системы и комплексы».
В результате освоения учебной дисциплины ЕН.02 Теория вероятностей и математическая статистика обучающийся должен обладать предусмотренными ФГОС по специальности СПО 09.02.01 Компьютерные системы и комплексы умениями:
У.1 вычислять вероятность событий с использованием элементов комбинаторики;
У.2использовать методы математической статистики;
знаниями:
З.1 основы теории вероятностей и математической статистики;
З.2 основные понятия теории графов;
В процессе освоения дисциплины у студентов формируются общие компетенции (ОК):
|
Код |
Наименование компетенций |
|
ОК 1. |
Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. |
|
ОК 2. |
Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. |
|
ОК 3. |
Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. |
|
ОК 4. |
Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития. |
|
ОК 5. |
Использовать информационно-коммуникационные технологии в профессиональной деятельности. |
|
ОК 6. |
Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями. |
|
ОК 7. |
Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий. |
|
ОК 8. |
Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. |
|
ОК 9. |
Ориентироваться в условиях частой смены технологий в профессиональной деятельности. |
В процессе освоения дисциплины у студентов формируются профессиональные компетенции (ПК):
|
Код |
Наименование компетенций |
|
ПК 1.2 |
Разрабатывать схемы цифровых устройств на основе интегральных схем разной степени интеграции. |
|
ПК 1.4 |
Проводить измерения параметров проектируемых устройств и определять показатели надежности. |
|
ПК 2.2 |
Производить тестирование, определение параметров и отладку микропроцессорных систем. |
Формами промежуточной аттестации по учебной дисциплине является:
в 3 семестре – дифференцированный зачет.
Перечень объектов контроля, форм контроля и показателей оценки по дисциплине приведены в таблице 1.
|
Таблица 1 – Перечень результатов обучения, контрольно-оценочных средств и показателей оценки
|
|||||
|
Результаты обучения |
Основные показатели оценки результата |
Наименование раздела (темы) |
Наименование контрольно-оценочного средства |
||
|
ПК, ОК (код)
|
(освоенные умения, усвоенные знания) |
Для текущего контроля |
Для промежуточной аттестации |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
ПК 1.2
|
У1, У2, З1, З2
|
Применение математических формул и математических методов к решению практических задач; Использование математического аппарата при разработке методов, средств и технологий в профессиональной деятельности; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1- №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ПК 1.4
|
У1, У2, З1, З2
|
Применение математических формул и математических методов к решению практических задач; Математическая обработка результатов тестирования приложений;
|
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики
|
Практические работы №1 – 8; Внеаудиторные самостоятельные работы №1- №10; Контрольные работы №1,2; Тесты №1-3. |
Тестовая зачетная работа по дисциплине |
|
|
ПК 2.2 |
У1, У2, З1, З2
|
Применение математических формул и математических методов к решению практических задач; Использование математического аппарата при разработке методов, средств и технологий в профессиональной деятельности; |
Раздел 2. Основы математической статистики
|
Практические работы №8; Внеаудиторные самостоятельные работы №8- №10; Контрольные работы №2; Тесты №3. |
Тестовая зачетная работа по дисциплине |
|
|
ОК1 |
У1, У2, З1, З2
|
Приведение примеров, подтверждающих значимость выбранной профессии; демонстрация интереса к будущей профессии через получение устойчивых результатов в процессе обучения; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1- №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК2 |
У1, У2, З1, З2
|
Успешное выполнение самостоятельной работы; Знание алгоритмов и демонстрация алгоритмического мышления; Демонстрация логического мышления обоснование выбора тех или иных математических методов и способов решения профессиональных задач; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1- №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК3 |
У1, У2, З1, З2
|
Умение решать нестандартные задачи с изменёнными данными, решение стандартных и нестандартных задач с использованием математических методов; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1- №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК4 |
У1, У2, З1, З2
|
Использование информационных систем при решении математических задач; Умение находить необходимую информацию в Интернете и других источниках; Чтение литературы профессиональной и общекультурной направленности; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1 - №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК5 |
У1, У2, З1, З2
|
Использование информационных системам при решении математических задач; Умение находить необходимую информацию в Интернете; Оформление результатов самостоятельной работы с использованием информационно- коммуникационных технологий; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1 - №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК6 |
У1, У2, З1, З2
|
Демонстрация способности к групповым методам работы; Умение выстраивать взаимоотношения с преподавателями; Демонстрация работы в малых коллективах над проектами; Взаимодействие с обучающимися и преподавателями в ходе обучения; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1 - №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК7 |
У1, У2, З1, З2
|
Умение организовывать деятельность членов команды при групповом методе работы; Демонстрация наличие качества лидера; Самоанализ и коррекция результатов собственной работы и работы членов коллектива; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1 - №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК8 |
У1, У2, З1, З2 |
Составление плана и работы над источниками литературы и сайтах Интернета; Самостоятельный, профессионально-ориентированный выбор тематики творческих работ; |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1 - №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
|
ОК9 |
У1, У2, З1, З2
|
Отслеживание изменений в области профессиональной деятельности; Осуществление поиска информации по заданию творческой работы; Анализ различных технологий в профессиональной деятельности с использованием математически обоснованных критериев. |
Раздел 1. Основы теории вероятностей Раздел 2. Основы математической статистики Раздел 3. Основные понятия теории графов |
Практические работы №1 – 10; Внеаудиторные самостоятельные работы №1 - №12; Контрольные работы №1,2,3; Тесты №1-4. |
Тестовая зачетная работа по дисциплине |
|
Контрольно-оценочные средства (далее КОС) текущего контроля включают:
1. Практические работы по дисциплине (Методические рекомендации по выполнению практических работ)
2. Внеаудиторные самостоятельные работы (Методические рекомендации по выполнению внеаудиторных самостоятельных работ)
3. Контрольно-измерительный материал (далее КИМ) (Приложение А)
3.1 КОС промежуточной аттестации 4 семестра в форме дифференцированного зачета включают:
1. Перечень вопросов для подготовки к дифференцированному зачету (Приложение В).
2. Задания для подготовки к дифференцированному зачету (Приложение С).
3. Контрольно-измерительные материалы (тесты) (Приложение D).
Условия выполнения задания на дифференцированном зачете:
1. Инструкция по выполнению:
Предлагаемая система контроля в тестовой форме.
Каждый правильно отверченный вопрос оценивается в 1 балл.
2.Деление на подгруппы не предусматривается
3.Время выполнения: 90 минут
4.Используемое оборудование:
Посадочные места по числу рабочих мест обучающихся, печатные варианты тестов, письменные принадлежности, основные математические формулы.
5. Критерии оценки:
Знания, умения обучающегося на экзамене оцениваются оценками: «отлично», «хорошо», «удовлетворительно», «неудовлетворительно».
Шкала оценки образовательных достижений
|
Процент результативности (правильных ответов) |
Оценка уровня подготовки |
|
|
балл (отметка) |
вербальный аналог |
|
|
90 ÷ 100% (36-40б.) |
5 |
отлично |
|
71 ÷ 89% (29- 35б.) |
4 |
хорошо |
|
50 ÷ 70% (20-28б.) |
3 |
удовлетворительно |
|
менее 50% |
2 |
неудовлетворительно |
Основная литература:
Основная литература:
1. Васильев А.А. Теория вероятностей и математическая статистика: [Электронный ресурс]: учебник и практикум для СПО/А.А. Васильев. – 2-е изд., испр. и доп. – М.: Издательство Юрайт, 2018. – 253с. – (Серия: Профессиональное образование).
Режим доступа: https://biblio-online.ru/viewer/teoriya-veroyatnostey-i-matematicheskaya-statistika-415807#page/2
Дополнительная литература:
1. Дадаян А.А. Математика: учебник/ А.А. Дадаян - 3-е изд.- М.: ФОРУМ: ИНФРА-М,2014-544с.
2. Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика [Электронный ресурс] : учебник / Е.С. Кочетков, С.О. Смерчинская, В.В. Соколов. – 2-е изд. – М.: ФОРУМ: ИНФРА-М, 2014. – 240 с. – (Профессиональное образование)
Режим доступа: http://znanium.com/bookread2.php?book=447828
Электронные образовательные ресурсы:
Российские ресурсы:
1. ЭБС «Издательство Лань» http://e.lanbook.com
2. Электронная библиотека ИРНИТУ http://elib.istu.edu
3. Научная электронная библиотека eLIBRARY.RU http://elibrary.ru
Приложение А
Контрольно-измерительные материалы текущего контроля по дисциплине ЕН. 02 Теория вероятностей и математическая статистика
Раздел 1.Основы теории вероятностей
Тест № 1
1. Инструкция по выполнению:
Внимательно прочитайте вопросы и предлагаемые варианты ответов. В тесте верным может быть только один вариант ответа.
Отвечайте только после того, как вы поняли вопрос и проанализировали все варианты ответа. Для экономии времени советуем пропустить задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
2. Место выполнения задания: кабинет математики аудитория №21.
3. Максимальное время выполнения тестов: 30 минут
4. Используемое оборудование:
- тесты для выполнения на бумажных носителях
- бланки ответов
5. Критерии оценки:
Количество баллов за сдачу теста переводятся в оценку по шкале:
86-100% -отлично
73-85%-хорошо
50-72%-удовлетворительно
меньше 50%- неудовлетворительно.
Задания для выполнения:
1)Какой вид имеет формула
размещения?![]()
а)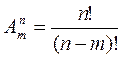 ; б)
; б)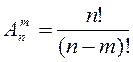 ; в)
; в)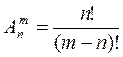 .
.
2)Какой вид имеет формула в классической теории вероятности?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3)Какой вид имеет формула сочетания?
а)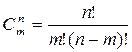 ; б)
; б)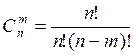 ; в)
; в)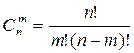 ;г)
;г)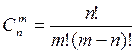
4) Посчитайте: ![]()
а)7,577; б)9,329; в)7,925; г)8,568.
5) Как обозначается вероятность?
а) n; б) P; в) q; г) m.
6) Посчитайте: ![]()
а) 70; б) 100; в) 90; г)89.
7) Как обозначается «число благоприятных событий» в классической теории вероятности?
а) n; б) p; в) m.
8) Решить задачу. Выбрать правильный вариант ответа.
В урне лежат шары двухзначные номера которых составлены из цифр1,2,3,4,5. какова вероятность вынуть шар с номером 15?
a)P=(A)=0,07; б)P=(A)=0,05; в) P=(A)=0,08; г)P=(A)=0,04;
9) Решить задачу. Выбрать правильный вариант ответа.
Сколькими способами можно составить патруль из двух полицейских, если на дежурство вышло 5?
а) 8; б) 15; в) 10; г) 11.
10) Решить задачу. Выбрать правильный вариант ответа.
В лотерее из 1.000 билетов имеются 200 выигрышных, вынимают на удачу 1 билет. Какова, вероятность того, что этот билет будет выигрышным?
а) 0,3; б) 0,2; в) 0,4.
11) Решить задачу. Выбрать правильный вариант ответа.
В соревнованиях участвуют 4 команды. Сколько вариантов размещения мест между ними возможно?
а) 21; б) 19; в) 24; г)27.
12)Раздел математики, изучающий решение задач выбора и перебора элементов в соответствие с какими-либо условиями.
а)Размещение; в)Комбинаторика;
б)Мат. ожидание; г)Дисперсия;
13)Формула ![]() соответствует:
соответствует:
а)Перестановке; в)Размещению;
б)Сочетанию;
14)Отношение числа элементарных событий, благоприятствующих событию А к общему числу равновозможных элементарных событий.
а)Комбинаторика; в)Вероятность;
б)Дисперсия; г)Мат. ожидание;
15)Сколько будет ![]()
а)3 б)6 в)24 г)120
16)В партии из 100 деталей имеются 5 бракованных. Определить вероятность того, что наугад взятая деталь окажется стандартной.
а)0,95; б)0,98; в)0,75; г)0,5.
17)В урне 4 белых и 7 черных шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара белые?
а)0,8 б)0,1 в)0,54 г)0,37
18)Вычислите: ![]()
а) 2; б)56;
в)30; г) ![]() .
.
19)Из 30 учеников спорткласса, 11 занимается футболом, 6 – волейболом, 8 – бегом, а остальные прыжками в длину. Какова вероятность того, что один произвольно выбранный ученик класса занимается игровым видом спорта?
а)![]() ; б) 0,5; в)
; б) 0,5; в)![]() ; г)
; г) ![]() .
.
20)Аня решила сварить компот из фруктов 2-ух видов. Сколько различных вариантов (по сочетанию фруктов) компотов может сварить Аня, если у нее имеется 7 видов фруктов?
а)14; б)10; в)21; г) 30.
Критерии оценки
«5» − 19 − 20 правильных ответов
«4» − 16 − 18 правильных ответов
«3» − 11 − 15 правильных ответов
«2» − менее 11 правильных ответов.
Ответы
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
б |
а |
а,в |
г |
б |
в |
в |
б |
в |
б |
в |
в |
б |
в |
г |
а |
б |
б |
а |
в |
Тест №2
1. Инструкция по выполнению
Внимательно прочитайте вопросы и предлагаемые варианты ответов. В тесте верным может быть только один вариант ответа.
Отвечайте только после того, как вы поняли вопрос и проанализировали все варианты ответа. Для экономии времени советуем пропустить задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
2. Место выполнения задания: кабинет математики аудитория №21.
3. Максимальное время выполнения тестов: 30 минут
4. Используемое оборудование:
- тесты для выполнения на бумажных носителях
- бланки ответов
5. Критерии оценки:
Количество баллов за сдачу теста переводятся в оценку по шкале:
86-100% -отлично
73-85%-хорошо
50-72%-удовлетворительно
меньше 50%- неудовлетворительно.
Задания для выполнения:
1.Раздел математики, изучающий решение задач выбора и перебора элементов в соответствие с какими-либо условиями.
а)Размещение; в)Комбинаторика;
б)Мат. ожидание; г)Дисперсия.
2.Формула ![]() соответствует:
соответствует:
а)Перестановке; б)Сочетанию; в)Размещению.
3.Всякое действие ли явление с несколькими различными исходами называется …
а)Испытанием; в)Событием;
б)Перестановкой; г)Размещением.
4.Два события называются несовместными, если появление одного из них …
а)Является больше другого; в)Не исключает появления другого.
б)Исключает появление другого;
5.События, которые в условиях испытания несовместимы.
а)Противоположные; б)Несуществующие; в)Невозможные.
6.Событие, которое непременно произойдет.
а)Полное; б)Достоверное; в)Невозможное.
7.Отношение числа элементарных событий, благоприятствующих событию А к общему числу равновозможных элементарных событий.
а)Комбинаторика; в)Вероятность;
б)Дисперсия; г)Мат. Ожидание.
8.Формула вероятности.
а)![]() б)
б)![]() в)
в)![]()
9.Сколько будет ![]()
а)3 ; б)6; в)24; г)120.
10.В партии из 100 деталей имеются 5 бракованных. Определить вероятность того, что наугад взятая деталь окажется стандартной.
а)0,95; б)0,98; в)0,75; г)0,5.
11.В урне 4 белых и 7 черных шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара белые?
а)0,8; б)0,1; в)0,54; г)0,37.
12.Какую формулу используют, когда количество испытаний велико?
а)Муавра-Лапласа; б)Бернулли; в)Комбинаторики.
13.Формула Бернулли
а)![]() б)
б)![]() в)
в)![]()
14.Монету бросают 8 раз. Какова вероятность, что 4 раза выпадет орел?
а)0,586371; б)0,273437; в)0,844653; г)0,765128.
15.В цехе 4 резервных мотора, работающих независимо друг от друга. Для каждого мотора вероятность того, что он включен в данный момент равна 0,1. Какова вероятность того, что в данный момент времени работает хотя бы один мотор?
а)0,831; б)0,765; в)0,291; г)0,545.
16.Локальная теорема Муавра-Лапласа.
а)![]() б)
б)![]() в)
в)![]()
17.Вероятность того, что сошедшая с конвейера деталь стандартная – 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей 356 окажутся стандартными.
а)0,0531; б)0,8341; в)0,0745; г)0,0136.
18.Величина, которая в результате испытания принимает только одно значение, заранее неизвестное.
а)Независимая; в)Неопределенная.
б)Случайная;
19.Случайная величина называется дискретной, если множество ее значений можно …
а)Перемножить; б)Перечислить; в)Сложить.
20.Если случайная величина может принимать все значения из промежутка (а,b), то она называется…
а)Случайной непрерывной; б)Несовместимой; в)Невозможной; г)Противоположной.
Ответы:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
в |
б |
а |
б |
а |
б |
в |
а |
г |
а |
б |
б |
а |
б |
в |
а |
а |
б |
б |
а |
Контрольная работа№1
1.Инструкция по выполнению
Решение приводится в тетрадях для контрольных работ.
2. Место выполнения задания: кабинет математики аудитория №21.
3. Максимальное время выполнения задания: 90 минут.
4. Используемое оборудование:
- плакаты с формулами Бернулли
5. Критерии оценки:
Нужно набрать баллы за выполнение заданий контрольной работы, которые переводятся в оценку согласно шкалы:
86-100% -отлично
73-85%-хорошо
50-72%-удовлетворительно
меньше 50%- неудовлетворительно.
1. Пусть проводится n = 6 независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна p = 0,1 . Найти вероятность того, что в данной серии испытаний событие A появится m = 3 раза.
2.
Стрелок делает 6 выстрелов по мишени.
Вероятность попадания при одном выстреле![]() . Найти вероятность того, что он
попал 4 раза.
. Найти вероятность того, что он
попал 4 раза.![]()
3. В результате обследования были выделены семьи, имеющие по 4 ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней:
а) одного мальчика;
б) двух мальчиков.
4. Статистика аудиторских проверок компании утверждает, что вероятность обнаружения ошибки в каждом проверяемом документе равна 0,1. Какова вероятность, что из десяти проверяемых документов девять из них не будет содержать ошибки?
5. По данным технического контроля 2% изготовленных станков нуждаются в дополнительной регулировке. Найти вероятность того, что из 6 изготовленных станков 4 нуждаются в дополнительной регулировке.
6. Производится 5 выстрелов в мишень. Вероятность попадания при каждом выстреле равна 3/4 . Найти вероятность того, что в мишени будет не менее трёх, но и не более четырёх пробоин. Найти наивероятнейшее число попаданий и соответствующую ему вероятность.
7. В каждой из восьми урн имеется 10 белых и 5 черных шаров. Из каждой урны извлекли по одному шару. Что вероятнее: появление двух черных и шести белых или трех черных и пяти белых шаров?
8. Вероятность поражения стрелком мишени равна 0,5. Найти вероятность того, что при 8 выстрелах мишень будет поражена от 5 до 7 раз.
9. Для вычислительной лаборатории приобретено девять компьютеров, причем вероятность брака для одного компьютера равна 0,1. Какова вероятность, что придется заменить более двух компьютеров.
10. В магазине 6 покупателей. Каждый может совершить покупку с вероятностью 0,4. Найти вероятность того, что не более двух человек совершат покупку.
11. Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из этих покупателей потребуется холодильник марки «Атлант», равна 0,4. Найти вероятность того, что холодильник потребуется:
а) не менее чем двум покупателям;
б) не более чем трем покупателям;
в) всем четырем покупателям.
12. Вероятность попадания стрелка в мишень при 1-м выстреле равна 0,5 .
Производится 5 выстрелов. Найти вероятность того, что стрелок промахнется не более двух раз.
13. Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет: а) менее 2 раз; б) не менее 2 раз.
14. Частица пролетает последовательно мимо 5 счетчиков. Каждый счетчик независимо от остальных отмечает ее пролёт с вероятностью 0,8. Частица считается зарегистрированной, если она отмечена не менее чем 2 счетчиками. Найти вероятность зарегистрировать частицу.
15. В телеателье имеется 7 телевизоров. Для каждого телевизора вероятность того, что в данный момент он включен, равна 0,6. Найти вероятность того, что в данный момент включены: а) четыре телевизора; б) хотя бы один телевизор; в) не менее трех телевизоров.
Раздел 2. Основы математической статистики
Тест №3
1. Инструкция по выполнению
Внимательно прочитайте вопросы и предлагаемые варианты ответов. В тесте верным может быть только один вариант ответа.
Отвечайте только после того, как вы поняли вопрос и проанализировали все варианты ответа. Для экономии времени советуем пропустить задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
2. Место выполнения задания: кабинет математики аудитория №21.
3. Максимальное время выполнения тестов: 30 минут
4. Используемое оборудование:
- тесты для выполнения на бумажных носителях
- бланки ответов
5. Критерии оценки:
Количество баллов за сдачу теста переводятся в оценку по шкале:
86-100% -отлично
73-85%-хорошо
50-72%-удовлетворительно
меньше 50%- неудовлетворительно.
Задания для выполнения:
1. Значением системы двух случайных величин является:
а) действительное число;
б) точка;
в) упорядоченная пара чисел.
2. Для системы двух случайных величин определяются:
а) математическое ожидание;
б) корреляционный момент (ковариация);
в) дисперсия;
г) коэффициент корреляции;
д) функция распределения вероятности.
3. Регрессией Y на X называется:
а) зависимость Y от X;
б) теснота связи Y и X;
в) изменение M(X/Y) при изменении Y;
г) прямая, на которой лежат точки, соответствующие значениям системы;
д) изменение M(Y/X) при изменении X.
4. Из того, что ковариация равна нулю вытекает, что
а) нет регрессии;
б) нет функциональной зависимости;
г) величины независимы;
д) нет линейной корреляции;
5. Прямая регрессии Y на X
имеет уравнение: ![]() . Какое из
перечисленных значений может принимать коэффициент корреляции?
. Какое из
перечисленных значений может принимать коэффициент корреляции?
а) 5; б) 0,5; в) – 1; г) 1; д) - 0,5.
6. Система непрерывных случайных величин имеет равномерное распределение вероятности на треугольнике с вершинами (0,0) (1,0) (0,-1). Тогда…
а) величины независимы;
б) имеется отрицательная корреляция;
в) имеется положительная корреляция;
г) имеется линейная корреляция.
7. Система непрерывных случайных величин имеет равномерное распределение вероятности на круге с центром (0,0) и радиусом 2. Тогда…
а) величины независимы; б) К>0; в) К=0;
г) величины связаны функционально.
8. Какие параметры имеет плотность нормального закона?
а) дисперсия; б) математическое ожидание ;
в) границы множества значений;
г) среднее квадратическое отклонение.
9. По критерию Пирсона проверяем гипотезу о равномерном распределении с параметрами а=1, b=3. В гистограмме – 20 столбцов. Сколько степеней свободы?
10. Гипотеза H0 : математическое ожидание М равно 20. За альтернативу можно принять…
а)![]() ;
б)
;
б)![]() ; в)
; в)![]() ;
г)
;
г)![]() ; д)
; д)![]() ;
е)
;
е)![]() .
.
Вариант 2
1. Множеством значений системы двух случайных величин является:
а) промежуток на числовой оси;
б) часть координатной плоскости;
в) числовая последовательность.
2. Статистическим аналогом закона распределения системы двух дискретных случайных величин является…
а) гистограмма; б) корреляционный момент (ковариация);
в) дисперсия; г) корреляционная таблица;
д) функция распределения вероятности.
3. Корреляцией Y и X называется:
а) зависимость Y от X;
б) теснота связи Y и X;
в) прямая, на которой лежат точки, соответствующие значениям системы;
г) изменение M(Y/X) при изменении X, обладающее свойством монотонности.
4. Из того, что нет регрессии Y на X вытекает, что…
а) K=0;
б) величины независимы;
в) нет регрессии X на Y.
5. Прямая регрессии Y на X
имеет уравнение: ![]() . Какое из перечисленных
значений может принимать коэффициент корреляции?
. Какое из перечисленных
значений может принимать коэффициент корреляции?
а) 5; б) 0,5; в) – 1; г) 1; д) - 0,5.
6. Система непрерывных случайных величин имеет равномерное распределение вероятности на треугольнике с вершинами (0,0) (1,0) (0,1). Тогда…
а) величины независимы;
б) имеется отрицательная корреляция;
в) имеется положительная корреляция;
г) имеется линейная корреляция.
7. Система непрерывных случайных величин имеет равномерное распределение вероятности на прямоугольнике с вершинами (0,0), (2,0), (2,3), (0,3). Тогда …
а) величины независимы; б) К>0; в) К=0;
г) величины связаны функционально.
8. Какие параметры имеет плотность равномерного закона?
а) дисперсия; б) математическое ожидание;
в) границы множества значений;
г) интенсивность потока событий .
9. По критерию Пирсона-Фишера проверяем гипотезу о распределении Пуассона. Параметр оцениваем по выборке. В гистограмме – 20 столбцов. Сколько степеней свободы?
10. Относительная частота равна 0,25. Гипотеза H0 для вероятности P
а)![]() ;
б)
;
б)![]() ; в)
; в)![]() ;
г)
;
г)![]() ; д)
; д)![]() .
.
Контрольная работа№2
1.Инструкция по выполнению
Решение приводится в тетрадях для контрольных работ.
2. Место выполнения задания: кабинет математики аудитория №21.
3. Максимальное время выполнения задания: 90 минут.
4. Используемое оборудование:
- плакаты с формулами числовых характеристик
5. Критерии оценки:
Нужно набрать баллы за выполнение заданий контрольной работы, которые переводятся в оценку согласно шкалы:
86-100% -отлично
73-85%-хорошо
50-72%-удовлетворительно
меньше 50%- неудовлетворительно.
Задания для выполнения:
1.Случайная выборка среди абитуриентов на вступительных экзаменах дала следующие набранные ими баллы:
12,12,14,11,11,12,14,10,12,13,11,15,10,13,11, 12,14,12,12,15.
Для данной выборки определить моду, медиану, размах выборки, объем выборки и построить таблицу распределения частот и относительных частот.
2. По заданной выборке определить моду, медиану, размах выборки, объем выборки и построить таблицу распределения частот и относительных частот:
1,0,1,3,2,3,4,0,5,3,3,2,3,0,1,0,3,5,2,4,1,2,1,0.
3. По заданной выборке определить моду, медиану, размах выборки, объем выборки и построить таблицу распределения частот и относительных частот:
200,200,201,203,202,203,204,204,205,203,203,202,203,201,201,200,205,202,204,200,300,200,200,300.
4.В группе 20 студентов, пятерым из них по 16 лет, семерым по 17 лет, четверым по 18 лет, троим по 19 лет и одному 21 год. Определить моду, медиану, размах, объем выборки возрастов и построить таблицу распределения частот и относительных частот.
5.Найдите эмпирическую функцию по данному распределению выборки:
|
|
4 |
7 |
8 |
|
|
5 |
2 |
3 |
6.Найдите эмпирическую функцию по данному распределению выборки:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
3 |
5 |
4 |
3 |
2 |
7.В результате эксперимента получена выборка объемом n=79:
2,4,2,4,3,3,0,2,0,6,1,2,3,5,2,4,3,3,5,1,0,2,4,3,2,2,7,3,1,3,3,3,1,1,2,3,1,4,3,1,7,4,3,4,2,3,2,3,6,1,4,3,1,4,5,3,4,7,4,5,3,6,4,1,3,2,4,1,3,1,0,0,4,6,4,7,4,1,3.
Построить таблицу распределения частот и полигон частот.
8.Построить гистограмму относительных частот по данному распределению выборки:
|
Частичный
интервал длиной |
Частота
|
|
[2;7) |
7 |
|
[7;12) |
10 |
|
[12;17) |
15 |
|
[17;22) |
5 |
|
[22;27) |
4 |
9.По результатам выборки:81,36,28,76,58 составить вариационный ряд и вычислить выборочную среднюю и выборочную дисперсию.
10.По выборке из задачи 7 вычислить значения числовых характеристик:
![]()
Раздел 3. Основные понятия теории графов
Тест №4
1. Инструкция по выполнению
Внимательно прочитайте вопросы и предлагаемые варианты ответов. В тесте верным может быть только один вариант ответа.
Отвечайте только после того, как вы поняли вопрос и проанализировали все варианты ответа. Для экономии времени советуем пропустить задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
2. Место выполнения задания: кабинет математики аудитория №21.
3. Максимальное время выполнения тестов: 30 минут
4. Используемое оборудование:
- тесты для выполнения на бумажных носителях
- бланки ответов
5. Критерии оценки:
Количество баллов за сдачу теста переводятся в оценку по шкале:
86-100% -отлично
73-85%-хорошо
50-72%-удовлетворительно
меньше 50%- неудовлетворительно.
Задания для выполнении:
1. На рисунке изображен :
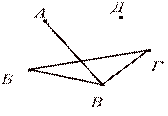
а) Полный граф; б) неполный граф; в) граф типа «дерево» г) нулевой;
2. Полный граф имеет 7 вершин, то количество ребер будет равно:
а) 14; б) 21; в) 7; г) 42.
3. Какие из указанных в графе на рисунке маршрутов являются путем?
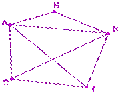 |
а) АВГВД б) АВГ в) АВДАБ г) АБВАД
4. Какие из указанных циклов являются простыми ?
а) АВГА б) АБВГБА; в) ВБАГВ; г) ДВАГВД
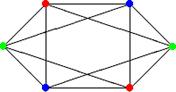
5. Хроматическое число графа на рисунке равно:
а)3; б)6; в)4; г)2.
6. Сколько ребер нужно провести чтобы достроить граф, изображенный на рисунке до полного?
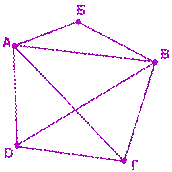
7.
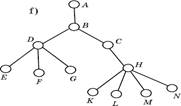 |
а) Полный граф; б) неполный граф; в) граф типа «дерево» г) нулевой;
8. Полный граф имеет 9 вершин, то количество ребер будет равно:
а) 18; б) 72; в) 9; г) 36.
9. Какие из указанных в графе на рисунке маршрутов являются путем?
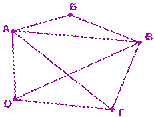
а) АВГВБ б) АВГВ в) АВДАГ г) АБВ
10. Какие из указанных циклов являются простыми ?
а) АВГДВА б) АБВГВА; в) ВБАГВ; г) ДВАГВД
11. Сколько ребер нужно провести, чтобы достроить граф, изображенный на рисунке, до полного?
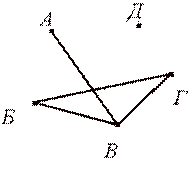
12. Назвать наименьшее число висячих вершин, дерева с 15-ю вершинами
Сформулируйте достаточные условия гамильтоновости графа.
Контрольная работа №3
1.Инструкция по выполнению
Решение приводится в тетрадях для контрольных работ.
2. Место выполнения задания: кабинет математики аудитория №21.
3. Максимальное время выполнения задания: 90 минут.
4. Используемое оборудование:
- плакаты с формулами графов
5. Критерии оценки:
Нужно набрать баллы за выполнение заданий контрольной работы, которые переводятся в оценку согласно шкалы:
86-100% -отлично
73-85%-хорошо
50-72%-удовлетворительно
меньше 50%- неудовлетворительно.
Задания для выполнении:
|
Вариант 1 |
Вариант 2 |
|
|
|
1) укажите степени вершин графа;
2) найдите длину пути из вершины V2 в вершину V5,
3) составьте маршрут длины 5, цепь и простую цепь, соединяющие вершину V2 и вершину V5.
4) Постройте простой цикл, содержащий вершину V4.
2. Найдите объединение и пересечение графов G1 и G2, дополнение для графа G1
|
Вариант 1
|
Вариант 2
|
3. Как называется вершина графа, имеющая степень, равную нулю?
4. Как называется вершина графа, имеющая степень, равную единице?
5. Как называется ребро графа, начало и конец которого совпадают?
6. Как называется граф без петель и кратных ребер, любые две
различные вершины которого соединены одним и только одним ребром?
Приложение В
Перечень вопросов для подготовки к дифференцированному зачету.
1. Предмет теории вероятностей и математической статистики.
2. Понятие случайного события. Операции над событиями. Частота и вероятность события.
3. Классическое определение вероятности. Вычисление вероятностей событий с использованием элементов комбинаторики.
4. Геометрическое определение вероятности.
5. Статистический подход к определению вероятности.
6. Теорема сложения вероятностей.
7. Условная вероятность. Теорема умножения вероятностей.
8. Формула полной вероятности. Формула Байеса.
9. Понятие дискретной случайной величины (ДСВ). Закон распределения и функция распределения дискретной случайной величины.
10. Числовые характеристики дискретных случайных величин.
11. Распределения дискретной случайной величины биномиальное, Пуассона.
12. Понятие непрерывной случайной величины (НСВ).
13. Функция распределения и плотность распределения непрерывной случайной величины.
14. Числовые характеристики непрерывных случайных величин.
15. Законы распределения непрерывной случайной величины: равномерное, нормальное и показательное распределение.
16. Генеральная совокупность и выборка. Сущность выборочного метода.
17. Дискретные и интервальные вариационные ряды. Полигон и гистограмма. Числовые характеристики выборки. Предварительная обработка статистических данных.
18. Эмпирическая функция распределения.
19. Графические представления дискретного и интервального вариационных рядов: полигон, гистограмма, кумулята
20. Точечные оценки параметров. Ошибки выборки.
21. Понятие доверительного интервала.
22. Случайные числа. Разыгрывание дискретных и непрерывных случайных величин.
23. Понятие графа и его элементов: вершина, ребро, петля, инцидентные вершины, смежные вершины, кратные и параллельные ребра, кратность и степень ребер.
24. Изолированная и висячая вершина. Нуль-граф. Полный и неполный граф. Дополнение графа. Ориентированный и неориентированный граф. Степени входа и выхода графа.
25. Способы задания графов. Матрица инцидентности и список рёбер.
26. Матрица смежности графа. Изоморфные графы.
27. Маршрут, длина маршрута, цикл, расстояние, цепь, путь.
28. Связный граф, компоненты связности.
29. Операции над графами.
30. Эйлеровые и гамильтоновые графы.
31. Цикломатическое число графа. Деревья, лес. Бинарные деревья.
32. Сети. Сетевые модели информации.
Приложение С. Типовые задания для подготовки к дифференцированному зачету.
1)Какой
вид имеет формула размещения?![]()
а)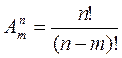 ; б)
; б)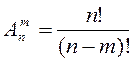 ; в)
; в)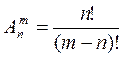 .
.
2)Какой вид имеет формула в классической теории вероятности?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3)Какой вид имеет формула сочетания?
а)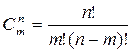 ;б)
;б)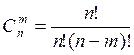 ; в)
; в)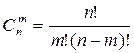 ;г)
;г)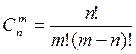
4)
Посчитайте: ![]()
а)7,577; б)9,329; в)7,925; г)8,568.
5) Как обозначается вероятность?
а) n; б) P; в) q; г) m.
6)
Посчитайте: ![]()
а) 70; б) 100; в) 90; г)89.
7) Как обозначается «число благоприятных событий» в классической теории вероятности?
а) n; б) p; в) m.
8) Решить задачу. Выбрать правильный вариант ответа.
В урне лежат шары двухзначные номера которых составлены из цифр1,2,3,4,5. какова вероятность вынуть шар с номером 15?
a)P=(A)=0,07; б)P=(A)=0,05; в) P=(A)=0,08; г)P=(A)=0,04;
9) Решить задачу. Выбрать правильный вариант ответа.
Сколькими способами можно составить патруль из двух полицейских, если на дежурство вышло 5?
а) 8; б) 15; в) 10; г) 11.
10)Решить задачу. Выбрать правильный вариант ответа.
В лотерее из 1.000 билетов имеются 200 выигрышных, вынимают на удачу 1 билет. Какова, вероятность того, что этот билет будет выигрышным?
а) 0,3; б) 0,2; в) 0,4.
11) Решить задачу. Выбрать правильный вариант ответа.
В соревнованиях участвуют 4 команды. Сколько вариантов размещения мест между ними возможно?
а) 21; б) 19; в) 24; г)27.
12)Раздел математики, изучающий решение задач выбора и перебора элементов в соответствие с какими-либо условиями.
а)Размещение; в)Комбинаторика;
б)Мат. ожидание; г)Дисперсия;
13)Формула ![]() соответствует:
соответствует:
а)Перестановке; б)Размещению; в)Сочетанию.
14)Отношение числа элементарных событий, благоприятствующих событию А к общему числу равновозможных элементарных событий.
а)Комбинаторика; в)Вероятность; б)Дисперсия; г)Мат. ожидание;
15)Сколько будет ![]()
а)3 б)6 в)24 г)120
16)В партии из 100 деталей имеются 5 бракованных. Определить вероятность того, что наугад взятая деталь окажется стандартной.
а)0,95; б)0,98; в)0,75; г)0,5.
17)В урне 4 белых и 7 черных шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара белые?
а)0,8 б)0,1 в)0,54 г)0,37
18)Вычислите: ![]()
а) 2; б)56;
в)30; г) ![]() .
.
19)Из 30 учеников спорткласса, 11 занимается футболом, 6 – волейболом, 8 – бегом, а остальные прыжками в длину. Какова вероятность того, что один произвольно выбранный ученик класса занимается игровым видом спорта?
а)![]() ; б) 0,5; в)
; б) 0,5; в)![]() ; г)
; г) ![]() .
.
20)Аня решила сварить компот из фруктов 2-ух видов. Сколько различных вариантов (по сочетанию фруктов) компотов может сварить Аня, если у нее имеется 7 видов фруктов?
а)14; б)10; в)21; г) 30.
21) Найдите формулу Бернули:
а)![]() ;
б)
;
б)![]() ; в)
; в)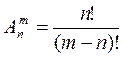
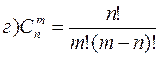
22)Чему равна сумма события и его противоположного?
а) p+q=0 ; б) p+q=1; в) p+q=2; г) p+q=3.
23) Монету подбрасывают 8 раз. Какова вероятность того, что 4 раза выпадет герб?
а) 1; б) 0,5; в) 0,34; г) 0,27.
24) Какую формулу используют, когда количество испытаний велико?
а)Муавра-Лапласа; б)Бернулли; в)Комбинаторики; г) Пуассона
25) Два события называются несовместными, если появление одного из них …
а)Является больше другого; в)Не исключает появления другого;
б)Исключает появление другого; г) Является меньше другого.
26) События, которые в условиях испытания несовместимы.
а)Противоположные; в)Невозможные;
б)Несуществующие; г) Пустые.
27)Раздел математики, изучающая решение задач выбора и перебора элементов в соответствии с каким-либо условиями.
а) размещение ; б)комбинаторика; в) математическое ожидание; г)дисперсия.
28) В партии из 100 деталей имеются 5 бракованных. Определить вероятность того что взятая наугад деталь является стандартной.
а) 0,95; б) 0,99; в) 0,85; г) 0,05.
29) Вероятность того, что день будет ясным равна 0,85. Вероятность того что день будет облачным равна?
а) 0,15; б) 0,99; в) 0,85; г) 0,05
30) Как называется произведение всех натуральных чисел от 1 до n ?
а) Математическое ожидание; б) Полигон; в) Факториал; г) Перестановка.
5 Критерии оценки
Студент, набравший 30 баллов, имеет 100 % правильных ответов. Оценка уровня подготовки выставляется согласно шкале оценки образовательных достижений.
Шкала оценки образовательных достижений
|
Процент результативности (правильных ответов) |
Оценка уровня подготовки |
|
|
балл (отметка) |
вербальный аналог |
|
|
90 ÷ 100% (29-30б.) |
5 |
отлично |
|
71 ÷ 89% (21- 28б.) |
4 |
хорошо |
|
50 ÷ 70% (15-20б.) |
3 |
удовлетворительно |
|
менее 50% |
2 |
неудовлетворительно |
Приложение D
Контрольно-измерительные материалы промежуточной аттестации
К каждому заданию теста даны три варианта ответа, из которых только один является верным. Выполните задание. В таблице ответов под номером задания (1–40) запишите номер выбранного Вами ответа.
1)Какой вид имеет формула размещения?![]()
а)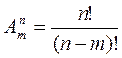 ; б)
; б)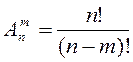 ; в)
; в)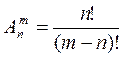 .
.
2)Какой вид имеет формула в классической теории вероятности?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Какой вид имеет формула сочетания?
а)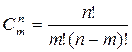 ;б)
;б)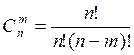 ;в)
;в)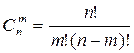 ; г)
; г)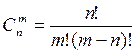 ;
;
4) Посчитайте: ![]()
а)7,577; б)9,329; в)7,925; г)8,568.
5) Как обозначается вероятность?
а) n; б) P; в) q; г) m.
6) Посчитайте: ![]()
а) 70; б) 100; в) 90; г)89.
7) По какой формуле находят Р ?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
8) Как обозначается «число благоприятных событий» в классической теории вероятности?
а) n; б) p; в) m.
9) Решить задачу. Выбрать правильный вариант ответа.
В урне лежат шары двухзначные номера которых составлены из цифр1,2,3,4,5. какова вероятность вынуть шар с номером 15?
a)P=(A)=0,07; б)P=(A)=0,05; в) P=(A)=0,08; г)P=(A)=0,04;
10) Какой вид имеет локальная формула Муавра Лапласа ?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]()
11) какой вид имеет формула Бернулли ?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г)![]() .
.
12) Решить задачу. Выбрать правильный вариант ответа.
Монету бросают 8 раз. Какова вероятность того, что 4 раза выпадет герб?
а) 0,273; б) 0,343; в) 0,478; г) 0,311.
13) Решить задачу. Выбрать правильный вариант ответа.
Сколькими способами можно составить патруль из двух полицейских, если на дежурство вышло 5?
а) 8; б) 15; в) 10; г) 11.
14) Какой вид имеет закон распределения дискретной случайной величины?
|
а) |
|
в) |
|
||||||||||||||||||||||||
|
б) |
|
|
|
15) Как вычислить вероятность этого события «выиграть две партии из четырех»?
а) ![]() ; б)
; б) ![]() ; в) нет правильного ответа.
; в) нет правильного ответа.
16) Решить задачу. Выбрать правильный вариант ответа.
Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.
а) 0,7412; б) 0,9423; в) 0.8414; г) 0,6314.
17) Какой вид имеет формула математического ожидания?
а) ![]() ; б)
; б) ![]() ;
;
в) нет правильного ответа.
18) Посчитать математическое ожидание:
|
X |
1 |
2 |
4 |
6 |
|
P |
0,2 |
0,15 |
0,35 |
0,3 |
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
г)
;
г) ![]() .
.
19) Решить задачу. Выбрать правильный вариант ответа.
В лотерее из 1.000 билетов имеются 200 выигрышных, вынимают на удачу 1 билет. Какова, вероятность того, что этот билет будет выигрышным?
а) 0,3; б) 0,2; в) 0,4.
20) Решить задачу. Выбрать правильный вариант ответа.
В соревнованиях участвуют 4 команды. Сколько вариантов размещения мест между ними возможно?
а) 21; б) 19; в) 24; г)27.
21.Раздел математики, изучающий решение задач выбора и перебора элементов в соответствие с какими-либо условиями.
а)Размещение; в)Комбинаторика;
б)Мат. ожидание; г)Дисперсия;
22.Формула ![]() соответствует:
соответствует:
а)Перестановке; в)Размещению;
б)Сочетанию;
23.Всякое действие ли явление с несколькими различными исходами называется …
а)Испытанием; в)Событием;
б)Перестановкой; г)Размещением;
24.Два события называются несовместными, если появление одного из них …
а)Является больше другого; в)Не исключает появления другого;
б)Исключает появление другого;
25.События, которые в условиях испытания несовместимы.
а)Противоположные; в)Невозможные;
б)Несуществующие;
26.Событие, которое непременно произойдет.
а)Полное; б)Достоверное; в)Невозможное;
27.Отношение числа элементарных событий, благоприятствующих событию А к общему числу равновозможных элементарных событий.
а)Комбинаторика; в)Вероятность;
б)Дисперсия; г)Мат. ожидание;
28.Формула вероятности.
а)![]() в)
в)![]()
б)![]()
29.Сколько будет ![]()
а)3 б)6 в)24 г)120
30.В партии из 100 деталей имеются 5 бракованных. Определить вероятность того, что наугад взятая деталь окажется стандартной.
а)0,95 б)0,98 в)0,75 г)0,5
31.В урне 4 белых и 7 черных шаров. Из урны одновременно вынимают 2 шара. Какова вероятность того, что оба шара белые?
а)0,8 б)0,1 в)0,54 г)0,37
32.Какую формулу используют, когда количество испытаний велико?
а)Муавра-Лапласа б)Бернулли в)Комбинаторики
33.Формула Бернулли
а)![]() в)
в)![]()
б)![]()
34.Монету бросают 8 раз. Какова вероятность, что 4 раза выпадет орел?
а)0,586371 б)0,273437 в)0,844653 г)0,765128
35.В цехе 4 резервных мотора, работающих независимо друг от друга. Для каждого мотора вероятность того, что он включен в данный момент равна 0,1. Какова вероятность того, что в данный момент времени работает хотя бы один мотор?
а)0,831 б)0,765 в)0,291 г)0,545
36.Локальная теорема Муавра-Лапласа.
а)![]() б)
б)![]() в)
в)![]()
37.Вероятность того, что сошедшая с конвейера деталь стандартная – 0,9. Найти вероятность того, что из 400 сошедших с конвейера деталей 356 окажутся стандартными.
а)0,0531 б)0,8341 в)0,0745 г)0,0136
38.Величина, которая в результате испытания принимает только одно значение, заранее неизвестное.
а)Независимая в)Неопределенная
б)Случайная;
39.Случайная величина называется дискретной, если множество ее значений можно …
а)Перемножить; б)Перечислить; в)Сложить;
40.Если случайная величина может принимать все значения из промежутка (а,b), то она называется…
а)Случайной непрерывной; б)Несовместимой; в)Невозможной; г)Противоположной;
Критерии оценки
Знания, умения обучающегося на экзамене оцениваются оценками: «отлично», «хорошо», «удовлетворительно», «неудовлетворительно».
Предлагаемая система контроля в тестовой форме, содержит сорок заданий с одним правильным вариантом ответа.
Шкала оценки образовательных достижений
|
Процент результативности (правильных ответов) |
Оценка уровня подготовки |
|
|
балл (отметка) |
вербальный аналог |
|
|
90 ÷ 100% (36-40б.) |
5 |
отлично |
|
71 ÷ 89% (29б-35б) |
4 |
хорошо |
|
50 ÷ 70% (20-28б.) |
3 |
удовлетворительно |
|
менее 50% |
2 |
неудовлетворительно |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.