Ещё раз о пользе тригонометрии. Графика PascalABC

Тригономе́трия — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613)

ВИКИПЕДИЯ

Ещё раз о пользе тригонометрии….

Создание динамических картинок на языке PascalABC.

1. Получение окружности

Вспомним  определение  тригонометрических функций   Sin α  и  Cos α:

А                                                                  Синусом острого угла  АСВ  прямоугольного треугольника АВС                                                                   называется отношение противолежащего катета АВ к гипотенузе АС                Косинусом острого угла  АСВ  прямоугольного треугольника АВС      называется отношение прилежащего катета ВС к гипотенузе АС        

В                             С

Построим систему прямоугольных (Декартовых) координат                                                                    у  

                                                                                                х                                                           О

Добавим на чертёж окружность,  центр которой совпадает с началом системы координат:                                                                          у   

                                                                                                    х                                                                   О

Выберем произвольную точку на  окружности  (для удобства и только…) в  I-ой четверти:                                                                              у

                                                                                     А

                                                                                                        х 

                                                                      О

Построим три отрезка из точки А:  радиус R,  перпендикуляры  к осям Ох и Оу,  а  точки пересечения с осями обозначим как    х1  и у1                                                 у

                                                                                                             А

                                                                                            у1

                                                                                                                                  Х                                                                                              О        х1   

              В общем случае получится прямоугольник   Ау1Ох1, в частном - квадрат с тем же названием.

Радиус R делит «прямоугольник Ау1Ох1»,  как  делит диагональ прямоугольник – на два прямоугольных треугольника.

Применим определения тригонометрических функций   Sin α  и  Cos α для нашего случая:

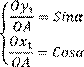
Заметим, что длины отрезков Ох1 и  Оу1 «численно» равны значениям координат точек х1 и у1, а отрезок ОА равен R  и поэтому перейдем к новому обозначению

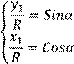
Откуда выразим координаты   х₁ и у₁      

                                                х₁ = R ∙ Cos α               (1)                                             у₁ = R ∙ Sin α                (2)

Делаем вывод:  Любая точка на окружности (мы брали произвольную точку) имеет координаты на плоскости, значения которых определяются   по формулам  (1) и (2), отличие заключается в величине острого (прямого, тупого, развернутого) угла. Меняя  размер угла и оставляя радиус неизменным, Мы  получим множество точек образующих окружность. Используемые обозначения:  х₁ и у₁ через х и у;   R через R, а угол α с помощью слова Alfa

Текст программы:

Program Krug;

Uses GraphABC, CRT;

Var  x,  y, R : integer;

Alfa  : real;

Begin

R := 40;

   Alfa  := 0 ;

While   Alfa <= 6.28  do      Begin             x := Round ( R * Cos (Alfa));            y :=Round (  R *   Sin (Alfa));

           SetPixel (x,y,clred );

Alfa:= Alfa + 0.0157;                                                                Результат исполнения программы End;  

End.                                                                                                        

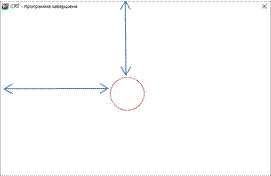
            Результат выполненной программы показан на рисунке (не тот, который мы хотели увидеть).  Проблема  в    различном представлении координат в математике и на компьютере (различие объясняется техническим устройством монитора и способом построения  изображения в нем). В математике начало системы  координат  там, где пересекаются оси, в компьютере в верхнем левом углу монитора, а Ось Оу (ось ординат) в математике  направлена вверх, на компьютере – вниз. Вот и  все различия. 

        Устраняем различие между координатами в различных системах координат добавляя в координаты компьютера поправки (смещение по осям Ох и Оу – dх и dу ), перемещая математическую систему координат в центр экрана (300; 200)   (dх = 300 pixel и dу = 200 pixel)

Текст исправленной программы:  

Program Krug;

Uses GraphABC, CRT;

Var    x,  y, R,  dx,  dy : integer; 

Alfa  :  real;                                         

Begin R := 40; dx := 300; dy:= 200;                                                                                                             Проблема устранена.

   Alfa  := 0;

While  Alfa <=  6.28   do

     Begin                                                                                                                        dy             x := dx + Round ( R * Cos (Alfa));                                                                              y := dy + Round (  R *   Sin (Alfa));                                         dx                                          SetPixel (x,y,clred );  

Alfa := Alfa + 0.0157;                                                               

End; End.

Построение эллипса,  геометрической фигуры имеющей два радиуса (вертикальный и горизонтальный)

По оси Ох

Program Elips;

Uses GraphABC, CRT;

Var    x,  y, R1,R2,  dx,  dy : integer;  

Alfa  :  real;                                         

Begin

R1 := 60; R2 := 40; dx := 300;

dy:= 200;                                                                dy:= 200;                                                               

   Alfa  := 0;

While  Alfa <=  6.28   do

     Begin                                                                Begin                                                          

            x := dx + Round ( R1 * Cos (Alfa));               x := dx + Round ( R1 * Cos (Alfa));              y := dy + Round (  R2 *   Sin (Alfa));             y := dy + Round (  R2 *   Sin (Alfa)); 

                                 SetPixel (x,y,clred );                                       SetPixel (x,y,clred );  

Alfa := Alfa + 0.0157;                                     Alfa := Alfa + 0.0157;                                     

                      End;                                                              End;

                      End.                                                              End.

Построение спирали  (изменение размера радиуса).  Количество колец спирали зависит от угла поворота Alfa ( один поворот – 6,28;   два поворота – 12,56; три поворота – 18,84 радиан и т.д. ,  можно применять  и произвольные значения – 10;  34,3  и любые другие  )

По часовой стрелке Против часовой стрелки

Program Spiral;

Uses GraphABC, CRT;

Var    x,  y,   dx,  dy : integer; Program Spiral;

Uses GraphABC, CRT;

Var    x,  y,   dx,  dy : integer;

Перейдем  к вопросу о динамических картинках:

      Перенос «математической системы координат»  из верхнего левого угла в центр экрана осуществлено использованием смещениями  dх и dу. Если заставить изменяться эти параметры и прорисовывать каждый отдельный случай получится «движение» (вводим внешний цикл со счетчиком  k и числом повторений, например 200). Будем  использовать  в новом варианте программы процедуры     CLRSCR – очистка экрана  и DELAY(m) – пауза в работе программы, для получения эффекта “24 кадра” или скорости движения (m – размер паузы в миллисекундах).

        Изменение величины смещения dх и dу зададим рекуррентными соотношениями:                                                           dх:= dх + t  и  dy:= dy + t

где t – изменение изменения координат (по сути вместе с паузой   DELAY(m)  мы получаем  скорость движения, заданное в пикселях/миллиcекунды).  

Program Krug;

Uses GraphABC, CRT;

Var  k, x,  y, R,  dx,  dy, t: integer;

Alfa  :  real;

Begin R := 40; dx := 20; dy:= 20; t:=2;

 For    k  := 0  to 200 do                  {количество разных смещений, смещения увеличиваются по порядку}       Begin

    Alfa  := 0;

While  Alfa <=  6.28  do      Begin

            x := dx + Round ( R * Cos (Alfa));            y := dy + Round (  R * Sin (Alfa));

           SetPixel (x,y,clred );

          Alfa  :=  Alfa  +  0.0157;

     End;

   DELAY (80);    CLRSCR;

   dx:= dx + t;

   dy:= dy + t;      End; End.

             Изменяя  t или делая их разными для dх и dу можно получить разные линейные  траектории . Используя тригонометрические функции Sin (k)  ИЛИ Cos (k) и обязательно округляя выражения до целого, с помощью  ROUND,  получим синусоидальную траекторию движения окружности

Убирая из программы  процедуру  CLRSCR ,  получим изображение фигуры из множества колец.

Например:

                                               По оси Оx:                                                               По оси Оy:

Убирая из программы  параметр  t  и переходя к старым значениям  dх и dу

dх := 300; dу:= 200;

На экране отобразится  «ТОРРОИД».

Program Tor;

Uses GraphABC, CRT;

Var    x,  y, x1,  y1,R,  dx,  dy, t: integer;

Alfa,k : real;

Begin R := 20; dx := 300; dy:= 200; t:=8;    k  := 0;

      while   k <= 6.28 do   {Большая окружность ( нить)}      Begin       x1:= dx+Round (  50 * Cos (k)) ;       y1:= dy+Round (  50 * Sin (k));              Alfa  := 0 ;

          while   Alfa <= 6.28 do           {Маленькие окружности (бусинки)}         Begin             x := x1 + Round ( R * Cos (Alfa));             y := y1 + Round (  R * Sin (Alfa));             alfa:= Alfa + 0.0157;

           SetPixel (x,y,clred );

        End;

   DELAY (80);     k:= k+0.0471;       End; End.

           Изменяя приращение  k,  равное 0,0471 радиан  в большую или меньшую сторону, мы изменим характер плотности прорисовки окружностей, расположенных (как бусы на нитке) на большой окружности (нити).

           Построение  цилиндра  и конуса (не по определению геометрии)  с использованием колец

(окружностей)

        Меняя законы изменения координат по осям Ох и Оу  мы расположим рисунки горизонтально или используя для обеих осей – под наклоном. Применяя знак “-“ получим инверсию (построение в обратном порядке)      

Построение  цилиндра  и конуса ( по определению в геометрии)  с использованием огибающей (окружностей)

Добавляя (изменяя ) координаты вершины конуса или центра основания мы получим наклонные тела:

    Построение произвольных «правильных фигур с количеством сторон  N

Внесём изменения в размер окружности (изменим радиус окружности), на базе которой строились правильные многоугольники:

Изменяя количество углов N можно поучить вращение правильного  N-многоугольника

Усложним задание  - создадим движение правильного многоугольника по спирали. Траектория подсвечивается точками красного цвета.

 Построим звезду.

Завершим построения движением Звезды по оси Ох

Желаю успеха!