Физика -10-дидактический материал

Приложение:

1.Задание на повторение.

Закрепление  пройденного материала.

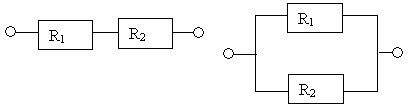
1.Что такое последовательное соединение?  (Последовательным считают, такое соединение проводников при котором , конец первого проводника соединяют с началом второго, конец второго с началом третьего и т.д.)

- Что такое параллельное соединение? (Это такое соединение при котором начало всех проводников присоединяются к одной точке электрической цепи, а их концы к другой)

2.Изображение соединений на доске выполняется учениками.

3.Сформулируйте закон Ома.

4.Помоги ученику правильно расставить формулы

На доске учениками маркером вносятся в таблицу правильные ответы.

Задание 2

Решение задач:

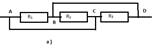
1. Найти сопротивление между точками A и D, если каждое из трех сопротивлений равно 1 Ом.

 ( Сопротивлением соединительных проводов пренебречь) 

2.Найти общее сопротивление на участке цепи, если все сопротивления равны по 2 Ом.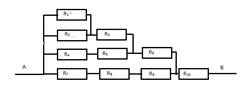

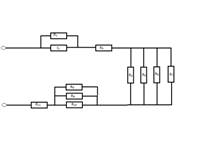
3.Найти сопротивление цепи если R₁ = 2 Ом, R₂ = 4 Ом, R₃ =1,5 Ом, R₄ = 2 Ом, R₅ = 3 Ом, R₆= 4 Ом, R₇ = 1 Ом, R₈ = R₉ = R₁₀ =7,5 Ом, R₁₁ = 1,5 Ом

Теоретическая часть задач (решение):

Каждой группе дается задание. Задание выполняется на флипчартах и презентуется у доски. Учащиеся записывают в тетради.

1.Найти сопротивление между точками A и D, если каждое из трех сопротивлений равно 1 Ом. ( Сопротивлением соединительных проводов пренебречь)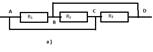  

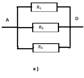
Т.к. точки А и С,  В и D   соединены проводниками, значит схему а) можно заменить на в). Общее сопротивление при этом вычисляется по формуле

Все три сопротивления одинаковы,  значит общее сопротивление вычисляется по формуле:

R=1/3 Ом = 0, 3 Ом

2.Найти общее сопротивление на участке цепи, если все сопротивления равны по 2 Ом.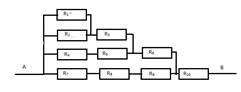

А. Найдем сопротивление R’ . Сопротивление R₁ и R₂ соединены параллельно, значит R’ ищем по формуле 

R’=1 Ом

Б. R’ и R₃ соединены последовательно и их общее сопротивление равно

R’’ =R’+R ₃ 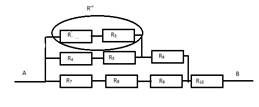 R’’= 3 Ом

В. Находим сопротивление R’’’ = R₄+ R₅ R’’’=4 Ом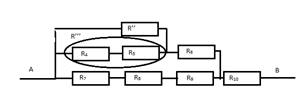

Г. Сопротивление R’’’’ определяем по формуле 

R’’’’= 1,7 Ом; R’’’’’ = R’’’’ + R₆; R’’’’’ = 3,7 Ом

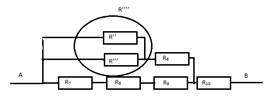
Д.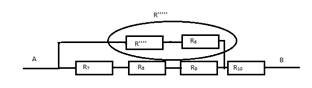 

Е. R’’’’’’ = R₇ +R₈ +R₉

R’’’’’’ = 6 Ом

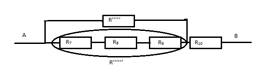
Ж. R’’’’’’’ определим по формуле 

R= 2,3 Ом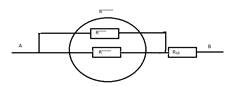

Общее сопротивление всей цепи равна  R= R’’’’’’’+ R₁₀

R = 4,3 Ом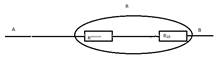

3.Найти сопротивление цепи если R₁ = 2 Ом, R₂ = 4 Ом, R₃ =1,5 Ом, R₄ = 2 Ом, R₅ = 3 Ом, R₆= 4 Ом, R₇ = 1 Ом, R₈ = R₉ = R₁₀ =7,5 Ом, R₁₁ = 1,5 Ом

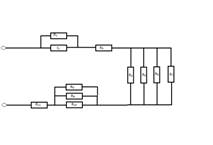
Рассмотрим соединение проводников. Оно смешанное и значит, ищем группы одинаково соединенных проводников и заменим их эквивалентной схемой.

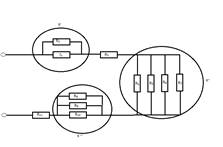Находим промежуточные сопротивления R^’, R^’’, R^’’’

R^’ = , R^’ =1,3 Ом,  =  +  +  + , R^’’ = 0,48 Ом,

Поскольку три сопротивления R₈, R₉, R₁₀ имеют одинаковое значение то сопротивление R^’’’рассчитываем по формуле

R^’’’ =  , R^’’’ = 2,5 Ом,

И наконец получили упрощенную схему

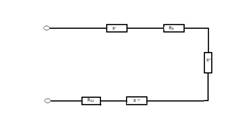
Все сопротивления соединены последовательно.

R = R’ + R₃ + R’’ + R’’’ + R₁₁, R = 7,31 Ом

4.Найти сопротивление каркаса куба, составленного из проволочек одинакового сопротивления.

В силу симметрии потенциал вершин куба 2, 3, 6 равны и вершин 4, 5, 7, значит  вершины 2,3,6 и 4,5,7 соединим проводниками, лишенными сопротивления, - «шинами». Сопротивление куба от этого не изменится. Таким образом, шины соединены друг с другом шестью проводниками: 2 – 7, 2 – 4, 3 – 5, 3 – 4, 6 – 7, 6 – 5.Общее сопротивление можно вычислить по формуле R = R’ + R’’ + R’’’

R’, R’’, R’’’ вычисляем по формулам:

R’ =  ; R’’ =  ; R’’’ =  ;

Конечное значение сопротивление ребер куба равна

R =  R₁

5.Найдите эквивалентное сопротивление бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый

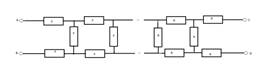
Для нахождения эквивалентного сопротивления цепи необходимо выделить общую секцию, которая бесконечно повторяется. Вполне очевидно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится, т.к. число элементов (секций) бесконечно. В силу вышесказанного, выделив повторяющуюся секцию в цепи и заменив сопротивление, остальной цепи искомым сопротивлением  R_х, получим эквивалентную схему. Найдем сопротивление цепи, предварительно записав выражение для  R_х через  R_x. Опуская промежуточные выкладки, получим: 

Или 

Учитель анализирует работу учащихся.

Теоретическая часть урока.

Смешанное соединение резисторов

Смешанное соединение резисторов. Смешанным соединением резисторов называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 1, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.

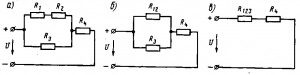
Рис. 1. Схемы смешанного соединения сопротивлений

Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R₁₂₃=R₁₂R₃/(R₁₂+R₃)=(R₁+R₂)R₃/(R₁+R₂+R₃).

При этом схема рис. 1, б заменяется эквивалентной схемой рис. 1, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:

R _эк = R₁₂₃ + R₄ = (R₁ + R₂) R₃ / (R₁ + R₂ + R₃) + R₄

Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.

Скачано с www.znanio.ru