


UO‘K: 53(075.3)
KBK 22.3ya721
F58
Muallifl ar:
N. Sh. Turdiyev – Mexanika, IV bob. “Statika va gidgodinamika”, VII bob. “O‘zgarmas tok qonunlari”, IX bob. “Turli muhitlarda elektr toki”;
K. A. Tursunmetov – V bob. “Mexanik tebranishlar va to‘lqinlar”;
A. G. Ganiyev – III bob. “Mexanikada saqlanish qonunlari”, VI bob. “Termodinamika”;
K. T. Suyarov – I bob. “Kinematika”, VII bob. “Elektrodinamika”;
J. E. Usarov – II bob. “Dinamika”, V bob. “Mexanik tebranishlar va to‘lqinlar”; A. K. Avliyoqulov – III bob. “Mexanikada saqlanish qonunlari”, VI bob. “Termodinamika”.
Taqrizchilar:
Sh. Usmanov – O‘zRFA Fizika-texnika institutining katta ilmiy xodimi, f-m.f.n.
B. Nurillayev – Nizomiy nomidagi TDPU kafedra mudiri, dotsent, pedagogika fanlari nomzodi,
Z. Sangirova – RTM bosh metodisti,
B. Saidxo‘jayeva – Toshkent viloyati, Pskent tumani 5-maktab fi zika o‘qituvchisi, O‘zbe kistonda xizmat ko‘rsatgan Xalq ta’limi xodimi.
F. Norqobilov – Toshkent shahar, Sergeli tumani, 303-maktab o‘qituvchisi,
Z. Tajibayeva – P. F. Borovskiy nomli tibbiyot kolleji o‘qituvchisi, N. Berdirasulov – Toshkent shahar, Sergeli tumani 104-maktab o‘qituvchisi,
SHARTLI BELGILAR:
–
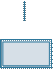 fi zik
kattaliklarga ta’rif; asosiy qonunlar;
fi zik
kattaliklarga ta’rif; asosiy qonunlar;
– muhim formulalar;
* – bu mavzular fi zikani chuqur o‘rganishga ishtiyoqi bo‘lgan o‘quvchi lar uchun mo‘ljallangan;
–
![]() o‘quvchi
tomonidan bajariladigan amaliy ish;
o‘quvchi
tomonidan bajariladigan amaliy ish;
– mavzu matnini o‘qib chiqqandan so‘ng, qo‘yilgan savoll arga javob bering;
Respublika maqsadli kitob jamg‘armasi mablag‘lari hisobidan chop etildi
|
ISBN 978-9943-4867-6-8 |
© N. Sh. Turdiyev va boshq. 2017 |
|
|
© “Niso Poligraf” nashriyoti |
|
|
(original-maket), 2017 |

![]()
Fizikada tabiatdagi jarayon va hodisalarni o‘rganishda o‘ziga xos tadqiqot metodlari mavjud.
Fizika eksperimental fan hisoblanadi. Shu bois tajriba o‘tkazish jarayoni alohida sharoitni talab qiladi. Bunda o‘rganilayotgan jarayonga tashqi ta’sir ko‘rsatilmasligiga harakat qilinadi.
Bundan tashqari, jarayonlarga tegishli fi zik parametrlar orasidagi bog‘lanishni matematik ifodalar orqali beriladi. Shunga ko‘ra fi ziklar jarayonlarning bundan keyingi borishini yoki oldin qanday bo‘lganligini juda aniq aytib berishga muvaffaq bo‘ldilar. Buyuk italyan fi zigi Galileo Galiley shunday deb yozgan edi: “Tabiat kitobi”ni tushunish uchun uning yozilgan tilini bilishing kerak. Bu til – matematikadir.
Kuzatishlardan ko‘pgina hodisalar uchun ma’lum bir qonuniyatlar mavjud ekanligi taxmin qilinadi. Bunday taxminlar ilmiy gipoteza deyiladi.
Gipotezani tekshirish uchun, olimlar tajriba (eksperiment) o‘tkazishadi. Buning uchun tabiiy sharoitga yaqinlashtirilgan maxsus sharoitlar yaratiladi.
Gipotezani shakllantirish va eksperiment o‘tkazish hamda uning natijalarini tushuntirish uchun, mazkur jarayon yoki hodisaning modeli tuziladi. Biror bir jarayonning modeli deyilganda uning ixchamlashgan, tartibga solingan, muhim jihatlari ajratib ko‘rsatilgan holati tushuniladi. Bunga misol sifatida moddiy nuqta va ideal gaz tushunchalarini misol qilib aytish mumkin.
Eksperiment o‘tkazish jarayonida tashqi ta’sirlardan to‘la qutulib bo‘lmaydi. Shunga qaramasdan, olingan natijaga ko‘ra ideal sharoitda qanday natija chiqishini aytib berish mumkin bo‘ladi. Bu ideal vaziyat ilmiy ideallashtirish deyiladi. Aynan mana shu hodisalar tashqaridan qaralganda murakkabga o‘xshasa-da, lekin ular bo‘ysunuvchi qonunlar sodda bo‘lishini ko‘rsatadi.
Fizik jarayonlar borishi haqidagi gipoteza tasdiqlansa, u fi zik qonunga aylanadi.
Mexanikaning asosiy mazmunini buyuk ingliz olimi Isaak Nyuton tomonidan shakllantirilgan uchta qonun, butun olam tortishish qonuni, elastiklik va ishqalanish kuchlariga doir qonuniyatlar tashkil etadi. Gaz jarayonlari uchun uning bosimi, hajmi va temperaturasi orasidagi bog‘lanishni ifodalaydigan qonunlar ochildi. Tinch holatda turgan zaryadlangan zarralar orasidagi o‘zaro ta’sir fransuz fi zigi Sharl Kulon tomonidan ochilgan qonunga bo‘ysunadi.
Keng qamrovli hodisalarni tushuntiradigan qonunlar to‘plami ilmiy nazariya deyiladi. Masalan, Nyuton qonunlari mexanikaning klassik nazariyasini tashkil etadi. Ingliz fi zigi D.K.Maksvell tomonidan shakllantirilgan qonunlar elektromagnitizm uchun klassik nazariya mazmunini tashkil etadi.
Ilmiy nazariya o‘z ichiga qonunlar bilan birgalikda bu qonunlarni shakllantirishda foydalanilgan fi zik kattaliklar va tushunchalarning ta’rifl arini ham oladi.
Eng muhimi, fi zik nazariyadagi barcha aniqlanadigan kattaliklar tajribada o‘lchana oladigan bo‘lishi kerak.
Barcha fi zik qonunlar va nazariyalar haqiqatga yaqin bo‘lishi kerak. Chunki nazariyani yaratishda har doim jarayon va hodisaning modelidan foydalaniladi. Shunga ko‘ra qonun va nazariyalarning qo‘llanilish chegarasi bo‘ladi, Masalan, klassik mexanika qonunlari faqat yorug‘lik tezligidan juda kichik tezlikda harakatlanadigan jismlar uchun o‘rinli bo‘ladi. Elementar zarralar tezlatgichlarida bu isbotlangan. Klassik mexanika, shuningdek, juda kichik massali zarralar (elektron) harakatini to‘g‘ri ifodalay olmaydi.
Yangidan topilgan fi zik nazariyalar avvalgilarini bekor qilmaydi, balki uni to‘ldiradi va aniqlashtiradi. Yangi fi zik nazariyaga qo‘yilgan muhim talablardan biri moslik prinsipidir. Bu degani belgilangan chegarada yangi nazariya, avvalgi nazariya bilan mos tushishi kerak.
![]() 1. Nima
sababdan fi zik nazariyadagi barcha aniqlanadigan kattalik lar tajribada
o‘lchana oladigan bo‘lishi kerak?
1. Nima
sababdan fi zik nazariyadagi barcha aniqlanadigan kattalik lar tajribada
o‘lchana oladigan bo‘lishi kerak?
2. Gipoteza qachon fi zik qonunga aylanadi?

![]()
7-sinfda siz turli mexanik harakatlar bilan tanishgansiz. Ularni birgalikda eslaylik:
1. To‘g‘ri chiziqli tekis harakat. Bunday harakatda jismning harakat trayektoriyasi to‘gri chiziqdan iborat bo‘ladi. Harakat tezligining kattaligi va yo‘nalishi o‘zgarmaydi. Bosib o‘tilgan yo‘l s = ·t formula bilan aniqlanadi.
2. To‘g‘ri chiziqli notekis harakat. Bunday harakatda jismning harakat trayektoriyasi to‘gri chiziqdan iborat bo‘ladi. Harakat tezligining kattaligi o‘zgaradi, lekin yo‘nalishi o‘zgarmaydi. Bosib o‘tilgan yo‘l s = o‘rt · t formula bilan aniqlanadi. Bunda o‘rt – jismning o‘rtacha tezligi.
3.
To‘g‘ri chiziqli tekis tezlanuvchan (sekinlanuvchan)
harakat. Bunday harakatda jism harakat trayektoriyasi to‘gri chiziqdan
iborat bo‘ladi. Harakat tezligining kattaligi bir tekisda ortib (kamayib)
boradi, ya’ni teng vaqtlar ichida bir xil kattalikka ortadi (kamayadi), lekin
yo‘nalishi o‘zgarmaydi. Bosib o‘tilgan yo‘l s = o· t ±
![]() formula bilan aniqlanadi (“+ˮ)
ishora tekis tezlanuvchan, a > 0, (“ – ˮ) ishora tekis
sekinlanuvchan (a < 0) bo‘lg anda qo‘yil adi).
formula bilan aniqlanadi (“+ˮ)
ishora tekis tezlanuvchan, a > 0, (“ – ˮ) ishora tekis
sekinlanuvchan (a < 0) bo‘lg anda qo‘yil adi).
4. Egri chiziqli tekis harakat. Egri chiziqli harakatning xususiy holi sifatida aylana bo‘ylab tekis harakatni olish mumkin. Bunday harakatda har doim tezlik yo‘nalishi uzluksiz o‘zgarib, trayektoriyaga urinma bo‘ylab yo‘nalgan bo‘ladi.Harakatning asosiy parametrlari: – chiziqli tezlik; ω – burchak tezlik; T – aylan ishlar davri; v – aylanishlar chastotasi; Syoy – yoy uzunligi; s – bosib o‘tilgan yo‘l.
Shuni ta’kidlash joizki, yuqorida keltirilgan harakatlarda jism faqat bitta harakatda qatnashgan hollar o‘rganilgan. Hayotda ko‘pincha jismlar bir vaqtning o‘zida bir nechta harakatda qatnashadi. Masalan, daryo bo‘ylab harakatlanayotgan kema, poyezd vagoni ichida yurib ketayotgan odam, uchib ketayotgan samolyotdan tashlangan yuk va h.k. Bunda daryoda harakatlanadigan kema o‘z dvigatelining tortish kuchi tufayli bir yo‘nalishda 1 tezlik bilan harakatlansa, suv uni 2 tezlik bilan oqim yo‘nalishida harakatlantiradi. Bu misollarda jismning ikkita harakatda qatnashayot ganligi ko‘rinib turibdi.
Shunday savol tug‘iladi. Kemaga o‘z dvigatelining tortish kuchi tufayli berilgan 1 tezlik daryoning oqish tezligiga bog‘liqmi? Uchib ketayotgan samolyotdan tashlangan yukning tushish vaqti samolyot tezligiga bog‘liqmi?
Tajribalar shuni ko‘rsatadiki, kemaning tezligi suvning oqish tezligiga, samo lyotdan tashlangan yukning tushish vaqti samolyot tezligiga bog‘liq emas!
Bundan shunday xulosa kelib chiqadi.
![]() Jism
qatnashayotgan harakatlar mustaqil bo‘lib, ularning harakat tezligi
(tezlanishi) bir-biriga bog‘liq emas. Bunga harakatlarning mustaqillik
prinsipi deyiladi.
Jism
qatnashayotgan harakatlar mustaqil bo‘lib, ularning harakat tezligi
(tezlanishi) bir-biriga bog‘liq emas. Bunga harakatlarning mustaqillik
prinsipi deyiladi.
Shunga ko‘ra istalgan murakkab harakatga, oddiy harakatlarning yig‘indisi deb qarash mumkin. Bu harakatlar bir-biriga ta’sir ko‘rsatmaydi. Agar ulardan biri o‘z harakatini o‘zgartirsa yoki butunlay to‘xtatsa, boshqasiga buning ta’siri bo‘lmaydi. Aynan mana shu prinsip asosida biz o‘rganayotgan jarayondagi vektor kattaliklarni alohida tashkil etuvchilarga ajratamiz. Ularni koordinata o‘qlariga proyeksiyalash ham shu prinsipga asoslangan. Tezlik vektorlarini qo‘shib natijaviy tezlikni chiqarish ham shu prinsip asosida bo‘ladi. Shunga asosan bir nechta harakatda qatnashgan jism harakati uchun quyidagilarni yozamiz:
![]()
 umum. = 1 + 2 + 3 + ... . + n,
umum. = 1 + 2 + 3 + ... . + n,
![]() umum. = 1 + 2 + 3 + ... . + n
(1.1)
umum. = 1 + 2 + 3 + ... . + n
(1.1)
![]() umum. = 1 + 2 + 3 + ... . + n
umum. = 1 + 2 + 3 + ... . + n
aumt2
= 0 + umt + 2 .
Ularga mos ravishda kattaliklarning x va y o‘qlariga bo‘lgan proyeksiyalari quyidagicha bo‘ladi:
sx = s0x + xt + ![]() , sy = s0y + yt +
, sy = s0y + yt + ![]() . (1.2)
. (1.2)
Masala yechish namunasi
Teploxodning tinch suvdagi tezligi 70 km/soat. U oqim bo‘ylab bir-biridan 36 km uzoqlikda joylashgan pristanlar oralig‘ini qancha vaqtda bosib o‘tadi? Daryo oqimining oqish tezligi 2 km/soat.
B e r i l g a n: F o r m u l a s i va y e c h i l i s h i:
s = 36 km s = · t; = tep + daryo;
tep. = 70 km/soat s = (tep + daryo) · t;
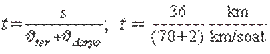 daryo. = 2 km/soat
daryo. = 2 km/soat
Bundan = 0,5 soat.
 Topish
kerak t – ? Javobi: 0,5 soat.
Topish
kerak t – ? Javobi: 0,5 soat.
1. Qanday hollarda tezlik vektori tashkil etuvchilarga ajratiladi?
![]() 2. Harakatlarning mustaqillik
prinsipi nimadan iborat?
2. Harakatlarning mustaqillik
prinsipi nimadan iborat?
3. Nima sababdan jism bir vaqtda bir necha harakatda qatnashayotgan bo‘lsa, harakatlar bir-biriga ta’sir ko‘rsatmaydi?
![]()
Biror jismni qo‘limizda ushlab turib, so‘ng uni qo‘yib yuborsak, jism tortish kuchi natijasida to‘g‘ri yer sirtiga tomon harakatlanadi. Jismning bunday harakati pastga qarab vertikal harakat deyiladi. Bunday harakatlar bilan siz 7-sinfda tanishgansiz. Bu mavzuda uni biz harakatlarning mustaqillik prinsipi nuqtayi nazaridan ko‘rib chiqamiz.
Jism vertikal harakatlanganda unga bitta yoki bir nechta kuchlar (og‘irlik kuchi, havoning qarshilik kuchi, Arximed kuchi) ta’sir qiladi. Jismning yuqoriga tik (vertikal) harakatida masalani soddalashtirish maqsadida havoning qarshilik kuchini va Arximed kuchini hisobga olmaymiz.
Jismni yuqoriga vertikal yo‘nalishda 0 boshlang‘ich tezlik bilan uloqtirib, uning harakatini kuzataylik (1.1-rasm). Agar jism faqat shu 0 tezlik bilan yuqoriga harakatlanganda u t vaqt ichida h1 = 0· t balandlikka ko‘tarilgan bo‘lar edi. Ammo yerning tortish kuchi ta’sirida shu t vaqt ichida jismning ko‘tarilish balandligi h2 = gt2/2 ga kamayadi. U holda jismning ko‘tarilishi mumkin bo‘lgan balandlik h = h1 – h2 ga teng bo‘ladi, ya’ni jismning harakat tenglamasi
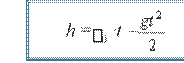 (1.3)
(1.3)
hmaxorqali ifodalanadi.
Yuqoriga vertikal otilgan jism harakati tekis sekinlanuvchan harakatdan iborat.
Jismning t vaqtdan keyingi tezligi
1.
1-rasm.
![]() (1.4)
(1.4)
ifoda yordamida aniqlanadi. Jism eng baland ko‘tarilish nuqtasiga yetganidan so‘ng to‘xtaydi ( = 0) va pastga qarab vertikal harakatini boshlaydi.
(1.4) ifodaning chap tomonini nolga tenglab, jismning ko‘tarilishi uchun ketgan vaqtini hisoblash ifodasiga ega bo‘lamiz:
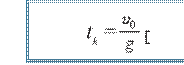 (1.5)
(1.5)
Jismning maksimal ko‘tarilish balandligi ifodasi quyidagicha bo‘ladi:
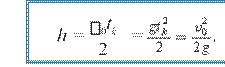 (1.6)
(1.6)
Havoning qarshiligi hisobga olinmas darajada kichik bo‘lgan sharoitda yuqoriga tik otilgan jismning ko‘tarilishi uchun ketgan vaqti uning tushish vaqtiga teng bo‘ladi, ya’ni tk = tt. Shuningdek, jism qanday tezlik bilan yuqoriga tik otilsa, u otilgan joyiga xuddi shunday tezlik bilan qaytib tushadi.
Pastga vertikal otilgan jismning harakati tekis tezlanuvchan harakatdan iborat bo‘ladi. Bunda jismning t vaqtdan keyingi tezligi
= 0 + gt (1.7) ifoda yordamida aniqlanadi. Pastga vertikal otilgan jism harakati tenglamasini quyidagicha yozamiz:
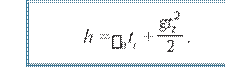 (1.8) Jismning vertikal
harakat qonuniyatlarini birinchi bo‘lib buyuk italiyan olimi G. Galiley
tajribalar asosida o‘rgandi. O‘tkazilgan tajribalar asosida jismlarning
vertikal tushishida ikkita qonuniyat borligi aniqlandi. Birinchidan, jismning
vertikal tushishi to‘g‘ri chiziqli tekis tezlanuvchan harakatdan iborat,
ikkinchidan, hamma jism erkin tushish vaqtida doimiy tezlanish bilan
harakatlanadi.
(1.8) Jismning vertikal
harakat qonuniyatlarini birinchi bo‘lib buyuk italiyan olimi G. Galiley
tajribalar asosida o‘rgandi. O‘tkazilgan tajribalar asosida jismlarning
vertikal tushishida ikkita qonuniyat borligi aniqlandi. Birinchidan, jismning
vertikal tushishi to‘g‘ri chiziqli tekis tezlanuvchan harakatdan iborat,
ikkinchidan, hamma jism erkin tushish vaqtida doimiy tezlanish bilan
harakatlanadi.
Jismning erkin tushishi tekis tezlanuvchan harakat bo‘lganligi inobatga olinsa, bu harakat uchun ham to‘g‘ri chiziqli tekis tezlanuvchan harakatning barcha tenglamalari o‘rinli bo‘ladi, faqat ularda a tezlanishni g erkin tushish tezlanishi bilan, s yo‘lni esa h balandlik bilan almashtirish kerak (1-jadval).
Erkin tushish tekis tezlanuvchan, (yuqoriga tik otilgan jism tekis sekinlanuvchan) harakatda bo‘lganligi uchun jism harakatining o‘rtacha tezligi quyidagi ifoda yordamida aniqlanadi:
o‘rt = ![]() . (1.9)
. (1.9)
Masala yechish namunasi
1. Balandligi 20 m bo‘lgan binodan tushayotgan jismning boshlang‘ich tezligi 15 m/s. Uning yerga to‘qnashish paytidagi tezligi nimaga teng?
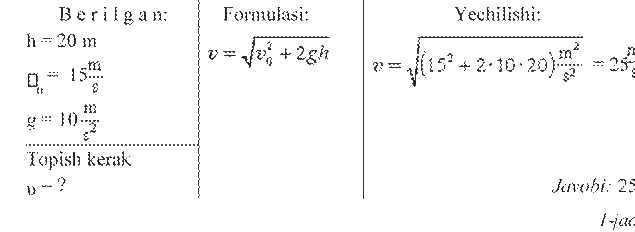
|
Tekis tezlanuvchan harakat tenglamalari |
Erkin tushishdagi harakat tenglamalari |
|
= 0 + at agar 0 = 0 bo‘lsa, = at |
= 0 + gt agar 0 = 0 bo‘lsa, = gt |
|
agar 0 = 0 bo‘lsa, s = |
h = 0t +
|
|
s
= |
h
= |
|
Agar 0= 0 bo‘lsa, = |
Agar 0= 0 bo‘lsa, = |
1. Yuqoriga vertikal
otilgan jism harakati qanday mustaqil ![]() harakat lardan
iborat?
harakat lardan
iborat?
2. Yuqoriga vertikal otilgan jism harakat tenglamasida nega tezlanish minus ishorada olingan?
3. Jism yuqoriga ko‘tarilayotganda uning tezlanishi o‘zgaradimi?
1. ![]() Yuqoriga
tik otilgan jismning ko‘tarilish vaqti bilan tushish vaqti tengligini
isbotlang.
Yuqoriga
tik otilgan jismning ko‘tarilish vaqti bilan tushish vaqti tengligini
isbotlang.
2. Jismni yuqoriga qanday tezlik bilan otsak, u otilgan joyiga xuddi shunday tezlik bilan qaytib tushishini isbotlang.
![]()
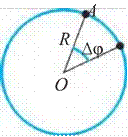 Siz 7-sinfda aylana bo‘ylab tekis harakat bilan
Siz 7-sinfda aylana bo‘ylab tekis harakat bilan
B tanishgansiz. Mazkur mavzuda aylana bo‘ylab notekis harakatni o‘rganamiz. Aylana bo‘ylab tekis harakatga tegishli fi zik kattaliklarni eslab ko‘raylik (1.2-rasm).
1. Aylana bo‘ylab tekis harakatlanayotgan moddiy
1. 2-rasm. nuqtaning vaqt birligi ichida yoy bo‘ylab bosib o‘tgan yo‘liga son jihatdan teng bo‘lgan kattalikka chiziqli
tezlik deyiladi va quyidagicha ifodalanadi.
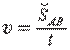 . (1.10).
. (1.10).
2. Aylana bo‘ylab tekis harakatda aylana radiusi burilish burchagining shu burilish uchun ketgan vaqtga nisbati burchak tezlik deyiladi:
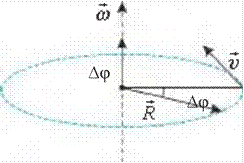
![]() . (1.11)
Burchak tezlik ham, chiziqli tezlik kabi vektor kattalik hisoblanadi. Uning
yo‘nalishi o‘ng vint (parma) qoidasiga binoan aniqlanadi. Bunda o‘ng vint
. (1.11)
Burchak tezlik ham, chiziqli tezlik kabi vektor kattalik hisoblanadi. Uning
yo‘nalishi o‘ng vint (parma) qoidasiga binoan aniqlanadi. Bunda o‘ng vint
kallagining aylanish yo‘nalishi moddiy ∆S nuqta aylanis hi bilan mos kelsa, uning uchining yo‘na lishi burchak tezlik vektori yo‘na lishi bilan mos tushadi (1.3-rasm). 1.3-rasm.
Ko‘pgina hollarda aylanma harakat qiluvchi jismlar o‘z aylanish tezligini o‘zgart iradi. Masalan, mashina joyidan qo‘zg‘alib, ma’lum bir tezlikka erishg uncha yoki tormozlanib to‘xtaguncha uning g‘ildiraklari shunday harakatlanadi.
![]() Aylana bo‘ylab
harakatlanayotgan jismning burchak tezligi vaqt davomida o‘zgarib turadigan
harakat o‘zgaruv chan aylanma harakat deyiladi.
Aylana bo‘ylab
harakatlanayotgan jismning burchak tezligi vaqt davomida o‘zgarib turadigan
harakat o‘zgaruv chan aylanma harakat deyiladi.
O‘zgaruvchan aylanma harakatlar orasida burchak tezligi ixtiyoriy teng vaqt oralig‘ida teng miqdorda o‘zgarib turadigan harakatlar ham uchraydi. Masalan, bekatga yaqinlashayotgan yoki undan uzoqlashayotgan avtobusning g‘ildiragi tekis o‘zgaruvchan aylanma harakat qiladi. Bunday harakatlarda burchak tezlikning o‘zgarish jadalligi burchak tezlanish deb ataluvchi fi zik kattalik bilan tavsifl anadi.
![]()
![]() Burchak
tezlik o‘zgarishining shu o‘zgarish uchun ketgan vaqtga nisbati bilan
o‘lchanadigan kattalikka burchak tezlanish deyiladi.
Burchak
tezlik o‘zgarishining shu o‘zgarish uchun ketgan vaqtga nisbati bilan
o‘lchanadigan kattalikka burchak tezlanish deyiladi.
.
(1.12)
Tekis o‘zgaruvchan aylanma harakatning burchak tezlanishi vaqt davomida o‘zgarmaydi, chunki uning burchak tezligi ham teng vaqt oraliqlarida teng miqdorga o‘zgaradi. Agar harakatlanayotgan moddiy nuqtaning boshlang‘ich burchak tezligi ω0, ∆t vaqt o‘tgandan keyingi burchak tezligi ω bo‘lsa, burchak tezligining o‘zgarishi ∆ω = ω – ω0 bo‘ladi. U holda (1.12) tenglama quyidagi ko‘rinishda yoziladi:
(1.13)
 Bundan burchak
tezlanishining birligi [ ε ] = kelib chiqadi. (1.13) ifodadan ixtiyoriy
vaqtdagi burchak tezlikni aniqlash formulasi kelib chiqadi:
Bundan burchak
tezlanishining birligi [ ε ] = kelib chiqadi. (1.13) ifodadan ixtiyoriy
vaqtdagi burchak tezlikni aniqlash formulasi kelib chiqadi:
![]() (1.14)
(1.14)
Burchak tezlik harakat davomida bir tekisda ortib borsa, aylanma harakat tekis tezlanuvchan bo‘ladi (ε > 0) (1.4-a rasm). Aylanma harakatning burchak tezligi aylanish jarayonida bir tekis kamayib borsa, bunday aylanma harakat tekis sekinlanuvchan deyiladi va ε < 0 bo‘ladi (1.4-b rasm).
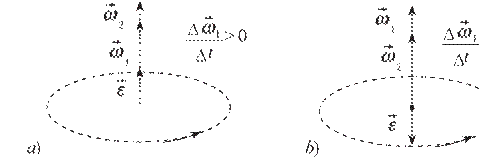
1.4-rasm.
Aylanma harakatda burchak tezlik vektor kattalik bo‘lganligi
uchun uning burchak tezlanishi ham vektor kattalikdir. Chunki, (1.13)
tenglikdagi ∆t skalyar kattalik. ω > ω0 bo‘lganda, ε >
0 bo‘lib, ![]() burchak tezlik vektori bilan bir tomonga,
ω < ω0
bo‘lganda, ε < 0 bo‘lib, burchak tezlikka teskari yo‘nalgan bo‘ladi.
burchak tezlik vektori bilan bir tomonga,
ω < ω0
bo‘lganda, ε < 0 bo‘lib, burchak tezlikka teskari yo‘nalgan bo‘ladi.
Tekis o‘zgaruvchan aylanma harakatning tenglamalarini hosil qilish uchun tekis o‘zgaruvchan to‘g‘ri chiziqli harakat tenglamalaridagi bosib o‘tgan s yo‘lni burilish burchagi φ bilan, tezlik ni burchak tezlik ω bilan va tezlanish a ni burchak tezlanish ε bilan almashtirish kifoya. Mazkur harakatlarning o‘zaro taqqoslangan tenglamalari quyidagi jadvalda keltirilgan:
![]() To‘gri
chiziqli tekis o‘zgaruvchan Tekis o‘zgaruvchan aylanma harakat harakat (a =
const)(ε = const) s = o‘rt · tφ = ωo‘rt · t
To‘gri
chiziqli tekis o‘zgaruvchan Tekis o‘zgaruvchan aylanma harakat harakat (a =
const)(ε = const) s = o‘rt · tφ = ωo‘rt · t
o‘rt = ![]() ωo‘rt =
ωo‘rt = ![]()
= 0 + a · tω = ω0 + ε · t
![]() s = 0 · t +
s = 0 · t +![]()
2 – 20 = 2a · s agar 0 = 0 bo‘lsa,
= a · t va
= ![]() agar a < 0 bo‘lsa,
agar a < 0 bo‘lsa,
= 0 – a · t s = 0 · t – ![]() 20 –
= 2a · s φ = ω0 · t +
20 –
= 2a · s φ = ω0 · t + ![]() ω2 –ω20 = 2ε · φ
ω2 –ω20 = 2ε · φ
agar ω0 = 0 bo‘lsa,
ω = ε
· t va ![]() agar ε < 0 bo‘lsa, ω
= ω0–
ε · t
agar ε < 0 bo‘lsa, ω
= ω0–
ε · t
φ = ω0 · t – ![]() ω20 –ω2 = 2ε · φ
ω20 –ω2 = 2ε · φ
Aylanma harakatda moddiy nuqtaning chiziqli tezligining son qiymati o‘zgaradigan hollar ham uchraydi. Bunday paytda moddiy nuqtaning chiziqli tezligi o‘zgarishi bilan bog‘liq tezlanish vujudga keladi. Bu tezlanish tezlikning son qiymati o‘zgarishi tufayli hosil bo‘lganligidan, uning yo‘nalishi tezlik yo‘nalishi bilan mos tushadi. Shunga ko‘ra uni urinma, ya’ni tangensial tezlanish deb ataymiz va uning ifodasi quyidagicha bo‘ladi:
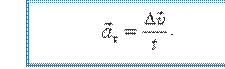 (1.15)
(1.15)
Shunday qilib, aylanma harakatlanayotgan moddiy nuqtaning chiziqli tezligi ham o‘zgarsa, uning umumiy tezlanishi
![]() =
τ + n yoki a =
=
τ + n yoki a = ![]() (1.16)
ifoda orqali aniqlanadi. Bu yerda: aτ= εR ga teng.
(1.16)
ifoda orqali aniqlanadi. Bu yerda: aτ= εR ga teng.
1.
![]() Tekis o‘zgaruvchan harakatning burchak tezlanishi deb
qanday fi zik kattalikka aytiladi? U qanday birlikda o‘lchanadi?
Tekis o‘zgaruvchan harakatning burchak tezlanishi deb
qanday fi zik kattalikka aytiladi? U qanday birlikda o‘lchanadi?
2. Burchak tezlik yo‘nalishi qanday aniqlanadi?
3. Normal yoki tangensial tezlanishi bo‘lmagan egri chiziqli harak at mavjudmi?
4. G‘ildirak tekis sekinlanuvchan harakat qilib 1 min. davomida chastotasini 300 1/min. dan 180 1/min gacha kamaytirdi. G‘ildirakning burchak tezlanishini va shu davrdagi to‘la aylanishlar sonini toping.
![]()
Kundalik turmushda harakatlanuvchi transport vositalarining harakati kuzatilsa, ularning dvigateli bir xilda ishlab tursa-da, ular turlicha tezlikda harakatlanishi kuzatiladi. Avtomobil tekis yo‘lda katta tezlik bilan qiyalikka chiqishda, botqoqli joylarda sekin yuradi. Xuddi shunday to‘qimachilikda, sanoatda ishlatiladigan dastgohlarda ham ularning turli qismlari turlicha tezlikda aylanayotganligini kuzatish mumkin. Kundalik turmushda ishlatiladigan tikuv mashunasida ham aylanma harakat va uni borib-keluvchi (ilgarilanma) harakatga aylantirib beruvchi mexanizmlar ishlatiladi (1.5-rasm).

1.5-rasm.
Bunday mexanizmlarda aylanma harakatni uzatishning friksion, tasmali va tishli g‘ildirak kabi usullari mavjud bo‘lib, mazkur mavzuda siz ular bilan tanishasiz.

 N
N
1 = 2 1 = 2
1.6-rasm. 1.7-rasm. 1.8-rasm.
Friksion usulda harakatni uzatish. Aylanma harakatni friksion usulda uzatish uchun har xil diametrli ikki g‘ildirak bir-biriga kuch bilan siqib turiladi. Ulardan biri soat strelkasining yo‘nalishi bo‘yicha aylansa, ikkinchisi ishqalanish kuchi ta’sirida harakatga kelib, soat strelkasining aylanishiga qarama-qarshi yo‘nalishida aylanadi (1.6-rasm).
Friksion uzatish usulidan, uzatiladigan quvvat uncha katta bo‘lmagan hollardagina foydalaniladi. Bu harakatda g‘ildiraklar bir-biriga nisbatan sirpanmaydi, shu sababli gildiraklar gardishlarining chiziqli tezliklarining modullari son jihatdan o‘zaro teng bo‘ladi: 1 = 2 yoki
 (1.17)
(1.17)
Harakatni tasmali uzatish. Aylanma harakatni tasmali uzatishda ikkita g‘ildirak bir-biriga tarang tortilgan tasma bilan biriktiriladi (1.7rasm). Bunda uzatish ishqalanish hisobiga amalga oshiriladi. Harakat uzatuvchi shkiv (g‘ildirak)ni yetaklovchi va harakatni qabul qiluvchi shkiv (g‘ildirak) yetaklanuvchi shkiv deyiladi. Tasmali uzatishda ham aylanayotgan g‘ildiraklarning chiziqli tezliklarining modullari o‘zaro teng: 1 = 2.
Burchak tezliklari esa g‘ildiraklarning radiuslari orqali o‘zaro quyidagi munos abatda bo‘ladi:
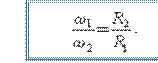 (1.18)
(1.18)
Harakatni tishli g‘ildiraklar orqali uzatish. Har xil diametri ikkita tishli g‘ildirakning tishlarini bir-biriga kiygizish orqali aylanma harakatni uzatish usuli tishli uzatish deb ataladi (1.8-rasm). Birinchi g‘ildirakdagi tishlar soni N1 bo‘lib, sekundiga ν1 marta aylansin, u bilan tishlashgan ikkinchi g‘ildirak esa N2 ta tishga ega bo‘lib, sekundiga ν2 marta aylansin. Tishlashish nuqtasida vaqt birligi ichida birinchi g‘ildirakning N1 · ν1 tishi o‘tganda, ikkinchisining N2 · ν2 tishi o‘tadi. Ikkala g‘ildirakning vaqt birligi ichida tishlashish nuqtasidan o‘tgan tishlar soni teng bo‘ladi, ya’ni:
N1 · ν1 = N2 · ν2. (1.19)
Bundan, bir-biriga tishlashgan g‘ildiraklardan har birining aylanish chastotasi uning tishlari soniga teskari proporsional bo‘ladi:
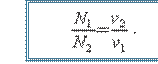 (1.20)
(1.20)
1. 9-rasmda yetaklovchi va yetaklanuvchi vallar bir tomonga va qaramaqarshi tomonga aylantiradigan holda tasmalar ulangan holatlari keltirilgan.

1.9-rasm.
![]() 1.
Aylanma harakatni friksion uzatishning qanday afzalliklari va kamchiliklari
bor?
1.
Aylanma harakatni friksion uzatishning qanday afzalliklari va kamchiliklari
bor?
2. Aylanma harakatni tasmali uzatishda ishlatiladigan mexa nizm larga misollar keltiring?
3. Aylanma harakatni tishli uzatish qanday amalga oshiriladi?
![]()
Balandligi h ga teng bo‘lgan stol ustida to‘g‘ri chiziq bo‘ylab harakatlanayotgan sharcha (zoldir)ning harakatini kuzataylik. Dastlab sharcha o‘z inersiyasi bilan stolning ustki qismida to‘g‘ri chiziqli harakat qiladi.
ySharcha stolning chetidan yerga yetib
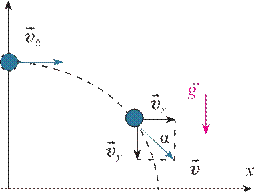 kelguncha ikkita harakatda qatnashadi.
kelguncha ikkita harakatda qatnashadi.
hYa’ni, dastlabki yo‘nalishda o‘z hara-
katini davom ettir ayotganligi hamda vertikal yo‘nal ishda harakatlanib, pastga tushayotg anligini ko‘ramiz. Sharchaning bu harakati biror balandlikdan gorizontal
0otilgan jismning harakatiga misoldir.
1. 10-rasm. Bu harakatni tavsifl ash uchun XOY koordinata sistemasini tanlab olib,
uni otilish nuqtasiga bog‘laymiz (1.10-rasm). Havoning qarshiligi hisobga olinmas darajada kichik bo‘lganda, jism gorizontal yo‘nalishda o‘zgarmas 0 tezlik bilan tekis harakat qiladi. Shuning uchun istalgan t vaqtdan keyingi gorizontal yo‘nalishdagi ko‘chishi yoki uchish uzoqligi quyidagicha hisoblanadi:
x = s = 0 · t. (1.21)
Jism tezligining x va y o‘qlardagi proyeksiyalari quyidagicha ifodalanadi:
x = 0, y = – g · t. (1.22)
Jism vertikal yo‘nalishda esa h balandlikdan boshlang‘ich tezliksiz tekis tezlanuvchan harakat qilib erkin tushadi. Shuning uchun istalgan t vaqtdan keyingi vertikal yo‘nalish bo‘yicha vaziyati quyidagicha hisoblanadi:
y
= h – ![]() . (1.23) Gorizontal otilgan
jismning XOY tekislikdagi harakat trayekt oriyas ining tenglamasi (1.21) va
(1.23) ifodalarga ko‘ra quyidagicha bo‘ladi:
. (1.23) Gorizontal otilgan
jismning XOY tekislikdagi harakat trayekt oriyas ining tenglamasi (1.21) va
(1.23) ifodalarga ko‘ra quyidagicha bo‘ladi:
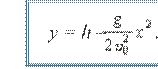 (1.24)
(1.24)
(1.24) ifoda parabola tenglamasini ifodalaydi. Demak, gorizontal otilgan jism parabola chizig‘i bo‘ylab harakat qiladi. h balandlikdan otilgan jismning uchish vaqti
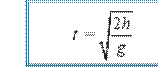 (1.25)
(1.25)
ifoda yordamida aniqlanadi. U holda jismning uchish uzoqligi
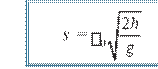 (1.26)
(1.26)
ko‘rinishni oladi.
Gorizontal otilgan jism bir vaqtning o‘zida gorizontal yo‘nalishda tekis va vertikal yo‘nalishda tekis tezlanuvchan harakat qilib, erkin tushadi. Harakatning oxiridagi (t vaqt o‘tgandan keyin) gorizontal va vertikal yo‘nalishidagi tezliklar mos ravishda x = 0 va y = g · t bo‘ladi. U holda jismning yerga tushishidagi tezligi quyidagicha aniqlanadi:
2 = 2x + y2 yoki
 (1.27)
(1.27)
Egri chiziq bo‘ylab harakatlanayotgan jismning ko‘chishi uning bosib o‘tgan yo‘liga teng bo‘lmaydi. Shuningdek, gorizontal otilgan jismning harakati davomida tezlik vektorining moduli va yo‘nalishi uzliksiz o‘zgarib turadi.
Masala yechish namunasi
1. Jism 35 m balandlikdan 30 m/s tezlik bilan gorizontal otildi. Uning yerga tushishdagi tezligini toping.
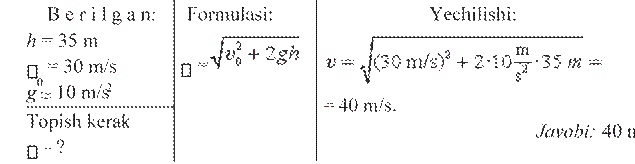
![]() 1. Gorizontal otilgan jism qanday
harakatlarda qatnashadi?
1. Gorizontal otilgan jism qanday
harakatlarda qatnashadi?
2. Gorizontal otilgan jismning trayektoriyasi qanday chiziqdan iborat?
3. Gorizontal otilgan jism tezligining gorizontal va vertikal tashkil etuvchilaridan qaysi biri jism harakati davomida o‘zgarmaydi?
4. Kundalik turmushdan mavzuga doir qo‘shimcha misollar keltira olasizmi?
5. Gorizontal yo‘nalishda boshlang‘ich 10 m/s tezlik bilan otilgan jismn ing uchish uzoqligi, otilish balandligiga teng bo‘ldi. Jism qanday balandlikdan otilgan?
![]()
 Gorizontga nisbatan
biror burchak ostida qiyalatib otilgan jism hara katini kuzatsak, uning avval
gori zontal yo‘nalishda otilgan nuqtasidan uzoqlashayotganligini hamda vertikal
yo‘nalishda ko‘tari layotganligini ko‘ramiz. Demak, gorizontga qiya otilgan jism
bir vaqtn ing
Gorizontga nisbatan
biror burchak ostida qiyalatib otilgan jism hara katini kuzatsak, uning avval
gori zontal yo‘nalishda otilgan nuqtasidan uzoqlashayotganligini hamda vertikal
yo‘nalishda ko‘tari layotganligini ko‘ramiz. Demak, gorizontga qiya otilgan jism
bir vaqtn ing
1.11-rasm. o‘zida gorizontal va vertikal yo‘nalishlar bo‘ylab harakatlanar
ekan. Gorizontal yo‘nalishda jism tekis harakatlanadi. U vertikal yo‘nalishda maksimal balandlikka ko‘tarilguncha tekis sekinlanuvchan, so‘ngra pastga qarab tekis tezlanuvchan harakat qiladi (1.11-rasm).
Gorizontga burchak ostida otilgan jismning harakat trayekto riyasi parabola ko‘rinishida bo‘ladi. Jism uchish jarayonida bir vaqtning o‘zida gorizontal va vertikal yo‘nalishlarda harakatlanayotganligi uchun jismning
0 boshlang‘ich tezligini gorizontal (ox) va vertikal (oy) tashkil etuvchilarga ajratamiz:
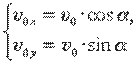 (1.28)
(1.28)
Hisoblarni soddalashtirish uchun havoning qarshiligini hisobga olmaymiz. Jismning istalgan t vaqtdan keyingi gorizontal yo‘nalishdagi ko‘chishi quyidagi
sx =0x · t = 0 · t · cosα (1.29) tenglikdan aniqlanadi.
Jismning istalgan t vaqtdagi gorizontal va vertikal yo‘nalishdagi tezligi quyidagi tengliklardan aniqlanadi:
x = x = 0 · cosα,
y = y – gt = 0 · sinα – gt. (1.30)
Gorizontga qiyalatib otilgan jismning harakati davomida tezligining gorizontal tashkil etuvchisi o‘zgarmasa-da, tezlikning vertikal tashkil etuvchisi ko‘tarilishda tekis kamayib boradi va trayektoriyaning eng yuqori nuqtasida nolga teng bo‘ladi. Demak, gorizontga burchak ostida otilgan jism trayektoriyasining eng yuqori nuqtasida minimal tezlikka ega bo‘ladi:
![]() min = 0 · cosα. (1.31)
min = 0 · cosα. (1.31)
Shundan so‘ng, jism shu nuqtadan 0xtezlik bilan gorizontal otilgan jism kabi harakat qiladi.
Jism trayektoriyasining eng yuqori ko‘tarilish nuqtasida y = 0 yoki 0sinα – gt = 0 munosabatdan ko‘tarilish vaqtini aniqlaymiz:
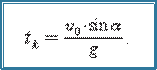 (1.32)
(1.32)
Jismning maksimal ko‘tarilish balandligi quyidagicha bo‘ladi
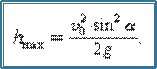 (1.33)
(1.33)
Jismning pastga qarab harakatlanish (tushish) vaqti, uning yuqoriga ko‘tarilish vaqtiga teng, ya’ni tk = tt. Bundan jismning umumiy uchish vaqti:
 (1.34)
(1.34)
Gorizontga burchak ostida otilgan jism gorizontal yo‘nalishda tekis harakat qiladi. Shu bois jismning uchish uzoqligi tezlikning faqat gorizontal tashkil etuvchisiga bog‘liq bo‘ladi. Uchish uzoqligini hisoblash uchun uchish vaqtining ifodasini sx = · t = 0x · t · cosα ifodaga qo‘yamiz va
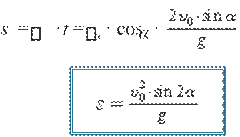 x 0x yoki
x 0x yoki
(1.35)
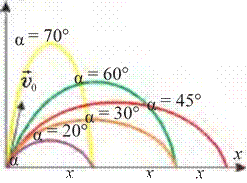
ega bo‘lamiz. Bu ifodadan ko‘rinadiki, gorizontga nisbatan burchak ostida otilgan jismning uchish uzoqligi otilish burchagiga bog‘liq. 1.12-rasmda jismning uchish uzoqligi va ko‘tarilish balandligining otilish burchagiga bog‘liqligi keltirilgan. Rasmdan ko‘rinadiki burchak ortib borishi bilan ko‘tarilish balandligi ham ortib boradi.
Jismning uchish uzoqligi dastlab otilish burchagi ortishi bilan ortadi va 45° ga teng bo‘lganda maksimal qiymatga erishadi. So‘ngra burchak ortishi bilan uchish uzoqligi kamayadi.
Gorizontga nisbatan burchak ostida otilg an jismning harakat trayektoriyasining tenglam asini keltirib chiqar amiz. Buning uchun
![]()
 y
y
y = oyt –
tenglamaga (1.29) tenglamadan t = 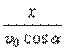 vaqtni
topib qo‘ysak, trayektoriya tenglamasi quyi da gi ko‘rinishda
vaqtni
topib qo‘ysak, trayektoriya tenglamasi quyi da gi ko‘rinishda
max1 max2 max3 ekanligi kelib chiqadi:
1.12-rasm.
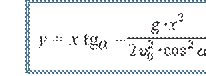 (1.36)
(1.36)
Demak, gorizontga qiya otilgan jism koordinata boshidan o‘tuvchi parabola bo‘ylab harakatlanar ekan, chunki x = 0 da y = 0 bo‘ladi. Bu tenglamadagi x2 oldidagi koeffi tsiyentning manfi y ishorali bo‘lganligi parabola shoxlarining pastga qarab yo‘nalganligini anglatadi.
Real sharoitlarda havoning qarshiligi uchish uzoqligiga kuchli ta’sir ko‘rsatadi. Masalan, 100 m/s bilan otilgan snaryad vakuumda 1000 m ga uchib borsa, havoda 700 m ga boradi. Tajribalar, otilish burchagini 30 – 40° qilib olinsa, otilgan jism eng uzoq masofaga borishini ko‘rsatadi.
Masala yechish namunasi
1. Koptok 10 m/s tezlik bilan gorizontga 30° qiyalatib otildi. U qancha balandlikka ko‘tariladi?
![]()
![]()
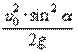
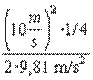 B
e r i l g a n: F o r m u l a s i: Y e c h i l i s h i: υo = 10 m/s
B
e r i l g a n: F o r m u l a s i: Y e c h i l i s h i: υo = 10 m/s
α = 30°hmax = g________________ = 9,81m/s2hmax = = 1,27 m.
Topish kerakJavobi: 1,27 m. h – ?
![]() 1.
Basketbolchi to‘pni to‘rga tushirish uchun o‘zining bo‘yini hisobga oladimi?
1.
Basketbolchi to‘pni to‘rga tushirish uchun o‘zining bo‘yini hisobga oladimi?
2. Gorizontga qiya otilgan jism havo qarshiligi hisobga olinganda qanday trayektoriya bo‘ylab harakatlanadi?
3. O‘q-yoy otish musobaqasida qatnashayotgan sportchi kamon o‘qini gorizontga nisbatan qanday burchak ostida otishi kerak?
![]() Hovlida yoki
vannada vodoprovod kraniga shlang ulab, suvni turli burchak ostida sepib
ko‘ring. Natijani tahlil qiling.
Hovlida yoki
vannada vodoprovod kraniga shlang ulab, suvni turli burchak ostida sepib
ko‘ring. Natijani tahlil qiling.
![]()
Ishning maqsadi. Jismning uchish uzoqligining otilish burchagiga bog‘liqligini tekshirish.
Kerakli asbob va jihozlar. Ballistik to‘pponcha, metall sharcha, o‘lchov lentasi, 2–3 varaq oq va qora qog‘oz (kopirovka).
1 5 Ishni bajarish tartibi.
1.
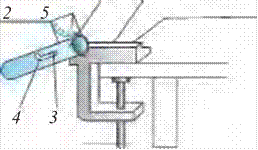 Ballistik to‘pponcha laborat or iya stoli chetiga
o‘rnatiladi (1.13-rasm).
Ballistik to‘pponcha laborat or iya stoli chetiga
o‘rnatiladi (1.13-rasm).
2. Ballistik to‘pponchaning qiyalik burchagini 30° qilib tutqich ga mahkamlanadi (Qiyalik burchagi to‘ppon chaga mahkamlangan transp ort ir yordam ida
1.13-rasm. aniqlanadi).
3. Tutqich orqaga tortiladi va uni stvol ilgagiga kiritiladi.
4. Metall sharcha stvol ichiga joylashtiriladi.
5. Tutqichni ilgakdan chiqarib yuboriladi va sharchaning tushish joyi aniqlanadi.
6. Tajriba yuqoridagidek kamida 3 marta takrorlanadi.
7. Ballistik to‘pponchaning qiyalik burchagini 45° ga qo‘yib tajribani takrorlanadi.
8. Hisoblangan kattaliklar qiymati quyidagi jadvalga yoziladi.
|
Otilish burchagi |
Tajriba |
l, uchish uzoqligi, (m) |
lo‘rt, (m) |
∆l, (m) |
Δlo‘rt, (m) |
|
30° |
1-tajriba |
|
|
|
|
|
2-tajriba |
|
|
|||
|
3-tajriba |
|
|
|||
|
45° |
1-tajriba |
|
|
|
|
|
2-tajriba |
|
|
|||
|
3-tajriba |
|
|
1.
![]() Gorizontga nisbatan qiya otilgan jism harakatining
trayekto riyasi qanday bo‘ladi?
Gorizontga nisbatan qiya otilgan jism harakatining
trayekto riyasi qanday bo‘ladi?
2. Gorizontga nisbatan qiya otilgan jismning uchish uzoqligi qanday kattaliklarga bog‘liq?
3. υ0 boshlang‘ich tezlik bilan burchak ostida otilgan jismning tushayotgan payt dagi tezligi qanday bo‘ladi va gorizont bilan qanday burchak tashkil qiladi?
4. Tajribada olingan natijalarga ko‘ra uchish uzoqligi va uchish vaqtining qiymati otilish burchagiga bog‘liqligini tahlil qiling.
1-mashq
1. Motorli qayiq daryoda manzilga yetib borish uchun 1,8 soat, qaytib kelish uchun esa 2,4 soat vaqt sarfl adi. Agar sol jo‘natilsa, manzilga qancha vaqtda yetib boradi? (Javobi: 14,4 soat).
2. Metrodagi eskalator odamni 30 s da yuqoriga olib chiqadi. Agar odam va eskalator birgalikda harakat qilsa, 10 s da ko‘tariladi. Eskalator tinch tursa odam qancha vaqtda yuqoriga chiqadi? (Javobi: 15 s).
3. Jism 80 m balandlikdan erkin tushmoqda. Tushishning oxirgi sekundidagi ko‘chishni toping. Harakat davomidagi o‘rtacha tezligini aniqlang. Jismning boshlang‘ich tezligini nolga teng deb hisoblang. (Javobi: 35 m, 20 m/s).
4. Agar vertikal yuqoriga otilgan jism yo‘lning oxirgi 1/4 qismini 3 s da bosib o‘tgan bo‘lsa, u qancha vaqt ko‘tarilgan? Uning boshlang‘ich tezligi qanday bo‘lgan? (Javobi: 60 m/s, 6 s).
5. Agar boshlang‘ich tezliksiz erkin tushayotgan jism oxirgi sekundda 75 m yo‘lni o‘tgan bo‘lsa, u qanday balandlikdan tushgan? Harakatning oxiridagi tezligi nimaga teng? (Javobi: 320 m, 80 m/s).
6. Ikki sharcha bir nuqtadan 20 m/s boshlang‘ich tezlik bilan 1 sekund vaqt intervali bilan yuqoriga vertikal otildi. Birinchi sharcha otilgandan qancha vaqt o‘tgach, sharlar uchrashadi? (Javobi: 2,5 s).
7. Maxovik aylanganda gardishidagi nuqtalar tezligi 6 m/s ulardan o‘qqa 1,5 sm yaqin masofada bo‘lgan nuqtalar tezligi esa 5,5 m/s bo‘lsa, maxovikning radiusi qancha? (Javobi: 18 sm).
8. Mexanik harakat I g‘ildirakdan II g‘ildirakka tasma orqali uzatiladi. Agar II g‘ildirakning burchak tezligi 100 πs–1, g‘ildiraklarning radiuslari mos ravishda 30 va 10 sm bo‘lsa, I g‘ildirak minutiga necha marta aylanadi? (Javobi: 300 marta).
9*. Magnitofon o‘ragichi 4 m/s tezlik bilan 40 s da tasmani o‘rab oldi. Agar o‘ragichning boshlang‘ich radiusi 2 sm, oxirgi radiusi 6 sm bo‘lsa, tasmaning qalinligini aniqlang. (Javobi: 0,063 mm).
10. h balandlikdan 0 boshlang‘ich tezlik
bilan gorizontal otilgan jism borib tushgan nuqtasiga aynan tushishi uchun uni h/3
balandlikdan qanday gorizontal tezlik bilan otish kerak? (Javobi: = ![]() 0).
0).
1. Motorli qayiqning daryo oqimi bo‘ylab suzgandagi qirg‘oqqa nisbatan tezligi 6 m/s, oqimga qarshi suzganda esa 4 m/s. Daryo oqimining tezligi (m/s) nimaga teng?
A) 0,5; B) 1; C) 2,5; D) 5.
2. Jism 15 m/s tezlik bilan vertikal pastga qarab tashlandi. U 2 s o‘tgach qanday tezlikka erishadi (m/s)?
A) 25; B) 35; C) 30; D) 45.
3. Jism qanday tezlik bilan vertikal otilsa, u 6 s dan so‘ng otilgan joyiga qaytib tushadi (m/s)?
A) 20; B) 35; C) 30; D) 40.
4. Yuqoriga tik otilgan jismning tezligi 2 s o‘tgach, ikki marta kamaydi. U qanday tezlik bilan otilgan?
A) 30; B) 40; C) 50; D) 60.
5. Massalari 100 g va 150 g bo‘lgan ikki metall sharcha bir xil tezlik bilan tik yuqoriga otildi. Ularning qaysi biri balandroq ko‘tariladi?
Havoning qarshiligini hisobga olmang.
A) massasi kichik bo‘lgan sharcha;
B) massasi katta bo‘lgan sharcha;
C) ikkalasi bir xil balandlikkacha ko‘tariladi;
D) berilgan ma’lumotlar yetarli emas.
6. Aylanma harakat 50 ta tishi bo‘lgan g‘ildirakdan 150 ta tishi bo‘lgan g‘ildirakka uzatilmoqda. Birinchi g‘idirak 2 s davomida bir marta to‘liq aylanib chiqsa, ikkinchi g‘ildirakning aylanish davri qancha?
A) 3 s; B) 7,5 s; C) 5 s; D) 6 s.
7. Egri chiziqli tekis harakatda quyidagi kattaliklarning qaysi biri o‘zgarmaydi?
A) oniy tezlik moduli; B) tezlanish moduli;
C) o‘rtacha tezlik moduli; D) tezlanish vektori.
8. Egri chiziqli tekis harakatda tezlanish vektorining yo‘nalishi qanday?
A) trayektoriyaning egrilik radiusi bo‘yicha markazga;
B) trayektoriyaga urinma;
C) harakat trayektoriyasi bo‘yicha;
D) egri chiziq radiusi bo‘yicha markazdan tashqariga.
9. 125 m balandlikdagi minoradan jism 30 m/s tezlik bilan gorizontal yo‘nalishda otildi. Jismning uchish uzoqligini aniqlang.
A) 300 m; B) 120 m; C) 240 m; D) 150 m.
10. Jism yerdan gorizontga nisbatan 30° burchak ostida 20 m/s boshlang‘ich tezlik bilan otildi. Boshlang‘ich tezlik vektorining gorizontal va vertikal tashkil etuvchilarini aniqlang (m/s).
A) 10 va 14,1; B) 17,3 va 10; C) 14,1 va 10; D) 20 va 10.
|
Ilmiy kuzatish |
Ilmiy tadqiqot metodi bo‘lib tizimli, faol, maqsadga yo‘naltirilgan bo‘ladi. |
|
Gipoteza |
Biror-bir jarayon, hodisa haqida taxminiy aytilgan fi kr. |
|
Tajriba (eksperiment) |
Gipotezaning to‘g‘riligini tekshirish uchun maxsus sharoitlarda o‘tkaziladi. |
|
Model |
Ixchamlashgan, tartibga solingan, muhim jihatlari ajratib ko‘rsatilgan holat. |
|
Ilmiy ideallashtirish |
Olingan natijaga ko‘ra ideal sharoitda qanday natija chiqishini aytib berish. |
|
Ilmiy nazariya |
Keng qamrovli hodisalarni tushuntiradigan qonunlar to‘plami. |
|
Moslik prinsipi |
Belgilangan chegarada yangi nazariyaning, oldingi nazariya bilan mos tushishi. |
|
Egri chiziqli tekis harakat |
Harakat trayektoriyasi egri chiziqdan iborat bo‘lgan, tezligining kattaligi o‘zgarmay digan, lekin yo‘nalishi trayektoriyaga urinma ravishda o‘zgara digan harakat. |
|
Harakatlarning mustaqillik prinsipi yoki superpozisiyasi |
Jism qatnashayotgan harakatlar mustaqil bo‘lib, ularning harakat tezligi (tezlanishi) bir-biriga bog‘liq emasligi. |
|
Yuqoriga qarab vertikal harakat |
Yer tortish kuchi yo‘nalishiga
qarama-qarshi harakat. Harakat tenglamasi h = 0 · t – |
|
Pastga qarab vertikal harakat |
Yer tortish kuchi
yo‘nalishidagi harakat. Harakat tenglamasi h = 0 · t + |
|
O‘zgaruvchan aylanma harakat |
Burchak tezligi vaqt davomida o‘zgarib turadigan aylanma harakat. |
|
Burchak tezlanish |
Burchak tezlik o‘zgarishining shu o‘zgarish uchun ketgan vaqtga nisbati
bilan o‘lchanadigan kattalik |
|
Aylana bo‘ylab tekis o‘zgaruvchan harakatda ixtiyoriy vaqtdagi burchak tezlikni aniqlash formulasi |
ω = ω0 + εΔt. |
|
Tangensial tezlanish |
Tezlikning son qiymati o‘zgarishi tufayli hosil bo‘ladi |
|
Egri chiziqli harakatning to‘la tezlanishi |
|
|
Friksion usulda harakatni uzatish |
Turli radiusli ikki g‘ildirak bir-biriga ta’sir (tegish) sirtlari orqali uzatiladigan harakat. |
|
Harakatni tasmali uzatish |
Harakat bir g‘ildirakdan ikkinchisiga tarang tortilgan tasma orqali uzatiladi. |
|
Harakatni tishli g‘ildiraklar orqali uzatish |
Har xil diametri ikkita tishli g‘ildirakning tishlarini bir-biriga kiyg‘izish orqali aylanma harakatni uzatish. |
|
Gorizontal otilgan jism ning uchish uzoqligi va yerga urilishdagi tezligi |
s =0 |
|
Gorizontga burchak ostida otilgan jismning minimal tezligi |
min = 0 · cosα. |
|
Gorizontga burchak ostida otilgan jismning ko‘tarilish balandligi |
|
|
Gorizontga burchak ostida otilgan jismning uchish vaqti |
t = |
|
Gorizontga burchak ostida otilgan jismning uchish uzoqligi |
|
|
Gorizontal otilgan jismning harakat trayektoriyasi tenglamasi |
y
= h – |
|
Gorizontga burchak ostida otilgan jismn ing harakat trayektoriyasi tenglamasi |
y = x · tgα – |

![]()
Bizni o‘rab turgan muhitdagi jismlarning harakati mexanika qonun lariga
bo‘ysunadi.
Jism harakatining o‘zgarish sabablarini XVI asr oxiri va XVII asr boshida ilk bor tajribalar vositasida batafsil o‘rgangan olim Galiley edi. Galiley jism harakatini o‘zgartish sababi haqida quyidagicha yozgan edi:
Agar jismga boshqa hech qanday jismlar ta’sir etmasa, jism Yerga nisbatan o‘zining tinch holatini yoki to‘g‘ri chiziqli tekis harakatini saqlaydi.
Galiley tomonidan o‘rnatilgan bu qonun mexanikaning asosiy qonunlarini tarkib toptirishda birinchi qadam bo‘ldi.
Bu qonunlarni ochish uchun Nyutonga hech qanday murakkab asbobuskunalar zarur bo‘lmagan. Buning uchun oddiy tajribalar yetarli bo‘lgan. Bundagi eng katta qiyinchilik jismlarning turli-tuman harakatlari ichidan eng muhimini, eng umumiysini ko‘ra olishdan iborat edi.
Dinamika grekcha “dynamis” so‘zidan olingan bo‘lib “kuch” degan ma’noni bildiradi. Agar biz qandaydir jismning harakatga kelganini ko‘rsak, unga ta’sir qilayotgan boshqa bir jismni ham ko‘ramiz. Boshqa jism, harakatga kelgan jismni tortishi, itarishi yoki unga masofadan turib ta’sir qilishi mumkin (masalan, magnitning temir sharga ta’siri). Yerdan biror balandlikka ko‘tarib qo‘yilgan jism qo‘yib yuborilsa pastga tushadi. Bu tajribalarning barchasida jism tezligining o‘zgarishi (ya’ni tezlan ish) har doim boshqa bir jismning ta’siri tufayli vujudga keladi. Bu ibora Nyuton mexanikasining eng muhim xulosasi hisob lanadi.
Jismlarning bir-biri bilan o‘zaro ta’sirlashish jarayoniga – o‘zaro ta’sir deyiladi. Fizikada barcha o‘zaro ta’sirlar albatta juft bo‘ladi. Ya’ni, har qanday ta’sir aks ta’sirni vujudga keltiradi.
Lekin bunday xulosaga darhol kelinmagan. Buyuk mutafakkir Aristotel jism harakatining o‘zgarishi sababini ochishga harakat qildi. Uning yozishicha, “Agar jismga itaruvchi kuch ta’sir etmay qolsa, harakatlanuvchi jism to‘xtab qoladi”. Yerga nisbatan bo‘lgan tinch holatni jismning tabiiy holati deb tushuntirgan.
O‘sha davrlarda Yerni Olamning markazi deb qarashganligi tufayli, muhim bir sabab bo‘lmasa, jism o‘zining tabiiy tinch holatiga qaytadi deb tushuntirishgan. Haqiqatan ham, tekis asfalt yo‘lda ketayotgan avtomobilning benzini tugab qolsa, dvigateli o‘chadi. Avtomobil biroz yurib to‘xtaydi. Xuddi shunday xulosani velosipedga, ko‘ldagi qayiqqa ham qo‘llash mumkin.
Olib borilgan kuzatishlar va xulosalar asosida dinamikaning birinchi qonuni topilgan edi. Uni quyidagicha ifodalanadi:
Inersial sistema deb ataluvchi shunday sanoq sistemalar mavjudki, undagi jism boshqa jismlardan yetarli darajada uzoq joylashgan bo‘lsa, tinch yoki to‘g‘ri chiziqli tekis harakatda bo‘ladi.
![]()
![]() Bu qonun
bir tomondan, inersial sanoq sistemasiga ta’rif bersa, ikkinchi tomondan,
haqiqatan ham, shunday sistemalar mavjudligini tekshirish imkoniyatini beradi.
Mexanikaning birinchi qonuni, inersial sanoq sistemasini alohida maxsus o‘ringa
qo‘yadi.
Bu qonun
bir tomondan, inersial sanoq sistemasiga ta’rif bersa, ikkinchi tomondan,
haqiqatan ham, shunday sistemalar mavjudligini tekshirish imkoniyatini beradi.
Mexanikaning birinchi qonuni, inersial sanoq sistemasini alohida maxsus o‘ringa
qo‘yadi.
Aylanayotgan qattiq jismning har bir nuqtasi tezlanish bilan harakatlanadi. Istalgan bo‘lakchaning tezlanishi jismdagi boshqa qismlarning ta’siri tufayli bo‘ladi. Boshqacha aytganda, qattiq jismni tashkil etgan bo‘lakchalar “erkin jism” bo‘la olmaydi va unga Nyutonning birinchi qonunini tatbiq etib bo‘lmaydi.
Shunday qilib, jismlarning tinch yoki to‘g‘ri chiziqli tekis harakat holatidan chiqish sababi boshqa jismlarning ta’siri ekanligini bilib oldik. Jismlarning bir-biriga bo‘lgan ta’siri kuch bilan xarakterlanadi.
Nuytonning ta’biricha, mexanikada, jismlarning bir-biriga ta’siri natijasida tezlanish olishiga sabab bo‘ladigan miqdoriy o‘lchamga kuch
deyiladi.
Bu kuchga sifat jihatidan berilgan ta’rifdir. Bu bilan mexanikada ikkita tasdiqni kiritdik:
1) jismlarda tezlanish, kuch ta’siri tufayli bo‘ladi;
2) tezlanish beruvchi kuch boshqa jismlarning ta’siri tufayli bo‘ladi.
Kuch tushunchasi ikkita jismga tegishlidir. Kuch vektor kattalik bo‘lib yo‘nalishga ega. Kuchni miqdoriy jihatdan aniqlash uchun uni o‘lchash kerak. Buning uchun uni boshqa bir etalon kuch bilan solishtiriladi.
![]() Tabiati
jihatidan qanday bo‘lishidan qat’i nazar, kuchlarning jismga bir vaqtdagi
ta’siri uning tezligini o‘zgartirmasa (ya’ni, unga tezlanish bermasa), moduli
jihatidan teng va qarama-qarshi yo‘nalgan bo‘ladi.
Tabiati
jihatidan qanday bo‘lishidan qat’i nazar, kuchlarning jismga bir vaqtdagi
ta’siri uning tezligini o‘zgartirmasa (ya’ni, unga tezlanish bermasa), moduli
jihatidan teng va qarama-qarshi yo‘nalgan bo‘ladi.
Tajribalar shuni ko‘rsatadiki, jismning olgan tezlanishi unga qo‘yilgan kuchdan tashqari jismning xossalariga ham bog‘liq. Demak, bu xossani aniqlashtirib olish zarur. Mexanikada bu xossa jism massasi bilan ta’rifl anadi.
Sizga 7-sinfdan ma’lumki, jismga qo‘yilgan kuchning jism olgan tezlanishiga nisbati o‘zgarmas kattalikdir
![]() =
const.
=
const.
![]() Jismga
tegishli
Jismga
tegishli ![]() nisbat bilan o‘lchanadigan kattalikka
inert massa deyiladi.
nisbat bilan o‘lchanadigan kattalikka
inert massa deyiladi.
Massa – jismning inertlik xossasini belgilaydi, ya’ni uning kuch ta’sirida qanchalik tezlanish olish qobiliyatini xarakterlaydi.
Massa tushunchasi kiritilganidan so‘ng, dinamikaning ikkinchi qonuni quyidagicha tavsifl anadi:
![]() Jismning olgan
tezlanishi qo‘yilgan kuchga to‘g‘ri, jismning massasida teskari proporsional
bo‘ladi:
Jismning olgan
tezlanishi qo‘yilgan kuchga to‘g‘ri, jismning massasida teskari proporsional
bo‘ladi:
(2.1)
 Bu ifoda tabiatning
shunday bir fundamental formulas iki, unga ulkan osmon jismlarin ing harakati
ham, shamol uchirg an mayda qum zarrasining haraka ti ham bo‘ysunadi.
Bu ifoda tabiatning
shunday bir fundamental formulas iki, unga ulkan osmon jismlarin ing harakati
ham, shamol uchirg an mayda qum zarrasining haraka ti ham bo‘ysunadi.
Yuqorida aytilganidek, o‘zaro
2.1-rasm. ta’sir har doim juft bo‘ladi. Masalan,
2.1-rasmda Alisher Bahodirga arqon
orqali ta’sir qilsa, Bahodir ham Alisherga aks ta’sir qiladi. Natijada Alisher ham, Bahodir ham tezlanish oladi.
Mazkur tajriba va shunga o‘xshash hodisalarni kuzatib, dinamikaning uchinchi qonuni chiqariladi:
Ta’sir har doim aks ta’sirni vujudga keltiradi. Ular son qiymati jihatidan bir-biriga teng bo‘lib, bir to‘g‘ri chiziq bo‘ylab qaramaqarshi yo‘nalgan:
![]() . (2.2)
. (2.2)
Bu kuchlar turli jismlarga qo‘yilganligidan, bir-birini muvozanatlay olmaydi. Ya’ni, o‘zaro ta’sirlashuvchi jismlar bu kuchlar ta’sirida alohidaalohida tezlanish oladi:
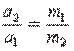 .
.
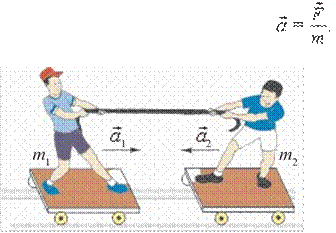
Masala yechish namunasi. F kuch ta’sirida m1 massali jism 2 m/s2 tezlanish oladi. m2 massali jism esa, shu kuch ta’sirida 5 m/s2 tezlanish oladi.
![]() Bu jismlar o‘zaro
ulansa, ular shu kuch ta’sirida qanday tezlanish bilan
Bu jismlar o‘zaro
ulansa, ular shu kuch ta’sirida qanday tezlanish bilan
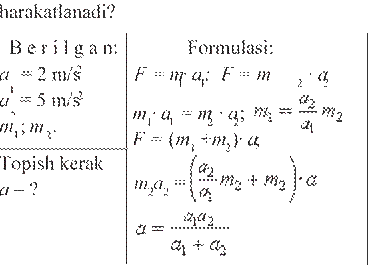 Y e c h i l i s h i:
Y e c h i l i s h i:
a = ![]() = 1,43
= 1,43![]() .
.
Javobi: 1,43 ![]() .
.
1.
Dinamika qonuni bo‘yicha Galiley aytgan fi krda qanday
xatolik bor ![]() edi?
edi?
2. Inert massa deganda nimani tushunamiz?
3. O‘zingizga ma’lum bo‘lgan o‘zaro ta’sirlarni ayting va misollar keltiring.
4. O‘zaro ta’sir natijasida nega jismlar har doim ham tezligini o‘zgartirmaydi?
![]()
Nisbiylik prinsipining ochilishiga asosiy sabablardan biri, Yerning harakati, aniqrog‘i uning o‘z o‘qi atrofi da aylanishi haqidagi gipoteza bo‘ldi. Shunday savol tug‘iladi: agar Yer o‘z o‘qi atrofi da aylanadigan bo‘lsa, nega biz uni Yer sirtida o‘tkazilgan eksperimentlarda sezmaymiz? Bu muammo ustidagi muhokamalarda qatnashgan o‘rta asrda yashab ijod qilgan Nikolay Orema (XIV asr), Olovuddin Ali al-Qushchi (XV asr)lar quyidagi xulosaga keldilar: Yerning aylanishi uning ustida o‘tkazilgan tajribalarga ta’sir qilmaydi.
Faraz qilaylik, siz sinfdoshlaringiz bilan birgalikda ulkan kemaning ichida, tashqi oynalari qoraytirilgan xonasida o‘tiribsiz. Shunda sinfdoshlardan biri hozir kema tinch turibdimi yoki harakatdami, degan savolni berdi. Tashqi palubaga chiqmasdan, buni qanday aniqlash mumkin? Bolalardan biri: “Kelinglar, tajriba o‘tkazib ko‘ramiz. Stoldagi buyumlardan birini tepadan pastga tashlab ko‘ramiz. Agar kema harakatsiz bo‘lsa, u vertikal tushadi. Harakatda bo‘lsa, tushish davrida kemaning poli oldinga ketib qolib, ozgina orqaga tushadiˮ, deb taklif qildi. Turli narsalar tashlab ko‘rilganda hammasi polga qarab tik holda aynan bir joyga tushdi. Demak, kema tinch turibdi, degan xulosaga kelindi. Tashqi palubaga chiqib qaralsa, kema bir tekisda chayqalmasdan suzib ketayotgan ekan! Demak, mexanik tajribalarni tinch turgan sinf xonasida o‘tkazilsa ham, to‘g‘ri chiziqli tekis harakatlanayotgan vagon yoki kema ichida o‘tkazilsa ham bir xil kechar ekan.
Bunga birinchi bo‘lib Galiley o‘z e’tiborini qaratgan edi. Galiley ham siz faraz qilgandek, ulkan kema ichida kuzatilayotgan mexanik jarayonlar, agar kema to‘g‘ri chiziqli tekis harakatlanayotgan bo‘lsa, xuddi tinch turganda qanday kechsa, shunday borishini yozib qoldirgan. Bunda sanoq sistemasi sifatida Yer emas, balki harakatlanayotgan vagon yoki kema olinadi.
Ti nch holatda turgan yoki nisbatan to‘g‘ri chiziqli tekis harakatlanayotgan sanoq sistemalari inersial sanoq sistemalari deyiladi.
Bir tekis oqayotgan daryoda kema oqim bo‘ylab suzib ketayotgan bo‘lsa, sanoq sistemasi sifatida qirg‘oqni yoki suvni olish mumkin. Xuddi shunday, to‘g‘ri chiziqli tekis harakatlanayotgan poyezd vagonida poyezd bo‘ylab harakatlanayotgan odam uchun sanoq sistemasi sifatida vagonni yoki Yerni olish mumkin. Odamning vagonga nisbatan tezligi , vagonning Yerga nisbatan tezligi u bo‘lsin. Agar odam vagonning harakat yo‘nalishi bilan bir xil yo‘nalishda harakatlansa, uning Yerga nisbatan tezligi u + bo‘ladi. Harakat qarama-qarshi yo‘nalishda bo‘lsa, u – bo‘ladi. Bunga Galileyning tezliklarni qo‘shish qoidasi deyiladi.
Tajribalar inersial sanoq sistemalarida soatlar bir xil davr bilan yurishini ko‘rsatdi.
Jismlarning ko‘chishi sanoq sistemalarida bir xil bo‘lmaydi. Chunki harakatlanayotgan vagon ichidagi odamning vagonga nisbatan ko‘chishi Yerga nisbatan ko‘chishidan kichik bo‘ladi. Jism massasini tinch holatda turgan vagon ichida o‘lchanganda ham, to‘g‘ri chiziqli tekis harakatlanayotgan vagonda o‘lchaganda ham bir xil chiqadi.
Shunday qilib, inersial sanoq sistemalarida vaqt, massa, tezlanish va kuch bir xil (invariant) bo‘ladi.
![]() Tinch holatda turgan sanoq sistemasida kuch F ga,
massa m ga, tezlanish a ga teng bo‘lsa, to‘g‘ri chiziqli tekis
harakatlanayotgan sistemada mos ravishda F', m' va a' bo‘ladi.
F = F'; m = m' va a = a' bo‘lganligi tufayli,
Nyutonning ikkinchi qonuni F = F' = ma yoki F' = m'a'
kabi ifodalanadi. Bundan Nyuton qonunlari barcha inersial sanoq
sistemalarida o‘rinli bo‘lishi kelib chiqadi.
Tinch holatda turgan sanoq sistemasida kuch F ga,
massa m ga, tezlanish a ga teng bo‘lsa, to‘g‘ri chiziqli tekis
harakatlanayotgan sistemada mos ravishda F', m' va a' bo‘ladi.
F = F'; m = m' va a = a' bo‘lganligi tufayli,
Nyutonning ikkinchi qonuni F = F' = ma yoki F' = m'a'
kabi ifodalanadi. Bundan Nyuton qonunlari barcha inersial sanoq
sistemalarida o‘rinli bo‘lishi kelib chiqadi.
Galileyning nisbiylik prinsipini umumiy holda quyidagicha ta’rifl ash mumkin:
Barcha inersial sanoq sistemalarida hamma mexanik jarayonl ar bir xilda kechadi.
Lekin shunday bir narsani esdan chiqarmaslik kerak. Biz bilamizki, to‘g‘ri chiziqli tekis harakat kamdan kam uchraydi. Bu degani inersial sanoq sistemalari juda kam mavjud bo‘ladi. Shunga ko‘ra har doim inersial sistemaga yaqin bo‘lgan sistemalar mavjud ekanligini esda tutishimiz kerak. Yerni biz inersial sanoq sistemasi deb qaraymiz. Xolbuki, u o‘z o‘qi atrofi da va Quyosh atrofi da aylanadi. Aylanma harakatda har doim tezlanish mavjud. Shunga qaramay Yerni inersial sanoq sistemasiga kiritamiz. Buning sababi shundaki, bu tezlanish juda kichik. Masalan, bu tezlanish ekvatorda 0,035 m/s2 ga teng bo‘lib, erkin tushish tezlanishiga nisbatan juda ham kichik. Shunga ko‘ra, uni hisobga olmasdan, harakatni tekis deb qarash mumkin. Yerning Quyosh atrofi da aylanishidagi tezlanish bundan ham kichik. Shunga ko‘ra Yerni inersial sanoq sistemasiga kiritamiz. Xuddi shunday, Yerga nisbatan to‘g‘ri chiziqli tekis harakatlanayotgan poyezdni ham inersial sanoq sistemasiga kiritsa bo‘ladi.
Yuqorida ta’kidlanganidek, to‘g‘ri chiziqli tekis harakatlanayotgan sistemalarda Nyuton qonunlari o‘rinli bo‘ladi. Agar sanoq sistemasi egri chiziqli yoki tezlanish bilan harakatlanayotgan bo‘lsa-chi? Bunday sistemalar noinersial sanoq sistemalari deyiladi. Qanday qilib noinersial sanoq sistemalarida Nyuton qonunlaridan foydalanish mumkin? Undan foydalanish uchun tezlanish hosil bo‘lish sababini eslaylik. Tezlanish hosil bo‘lish sababi – bu kuch. Demak, Nyutonning ikkinchi qonunidan foydalanish uchun jismga boshqa jismlar tomonidan ta’sir qilayotgan kuchlar bilan birgalikda inersiya kuchini kiritamiz. Inersiya kuchi jismga boshqa jismlar tomonidan emas, balki sanoq sistemasi tezlanish bilan harakatlanishi tufayli ta’sir qiladi. U holda Nyutonning ikkinchi qonuni quyidagi
![]() (2.3) ko‘rinishida bo‘ladi.
(2.3) ko‘rinishida bo‘ladi.
![]() Inersiya kuchining ifodasini topish uchun tezlanishning
absolyut qiymati
Inersiya kuchining ifodasini topish uchun tezlanishning
absolyut qiymati ![]() ab va tezlanishning nisbiy qiymati
ab va tezlanishning nisbiy qiymati ![]() nis ning ayirmasidan
foydalanamiz. U
nis ning ayirmasidan
foydalanamiz. U
holda inersiya kuchi ifodasi quyidagicha bo‘ladi:
![]() (2.4)
(2.4)
![]()
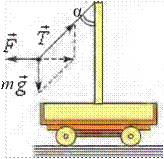 Aytilganlarni
misolda qaraylik. Kichik bir aravachada ustun o‘rnatilgan bo‘lib, unga
2.2-rasmda ko‘rsatilganidek mayatnik osilgan. Aravacha Yerga nisbatan
Aytilganlarni
misolda qaraylik. Kichik bir aravachada ustun o‘rnatilgan bo‘lib, unga
2.2-rasmda ko‘rsatilganidek mayatnik osilgan. Aravacha Yerga nisbatan ![]() ab doimiy tezlanish
bilan harakatlanmoqda. Mayatnik aravachaga nisbatan qo‘zg‘almas: anis = 0. Mayatnikka m
, m i
va
ab doimiy tezlanish
bilan harakatlanmoqda. Mayatnik aravachaga nisbatan qo‘zg‘almas: anis = 0. Mayatnikka m
, m i
va ![]() kuchlar ta’sir qiladi.
kuchlar ta’sir qiladi.
2.2-rasm. – mayatnik osilgan ipning taranglik kuchi. Lekin bu kuchlar mayatnikka tezlanish bermaydi. Nyutonning
![]() ikkinchi qonuni
bajarilishi uchun unga inersiya kuchi
ikkinchi qonuni
bajarilishi uchun unga inersiya kuchi ![]() ni kiritish kerak. U holda m
+ + i =
0.
ni kiritish kerak. U holda m
+ + i =
0.
Demak, Nyutonning ikkinchi qonuni shartli ravishda bajariladi.
Mayatnikning og‘ish burchagi  .
.
1. Inersial sanoq sistemalari deganda nimani tushunamiz?
![]() 2. Inersial sanoq sistemalarida qanday
fi zik kattaliklar bir xil bo‘ladi?
2. Inersial sanoq sistemalarida qanday
fi zik kattaliklar bir xil bo‘ladi?
3. Nyutonning uchinchi qonuni inersial sanoq sistemalari uchun o‘rinlimi?
![]()
Siz 7-sinfda Yer o‘z atrofi da doimiy tortishish maydoni hosil qilishini va shu maydon orqali jismlarni o‘ziga tortib turishini bilib olgansiz. Demak, Yerda bo‘ladigan barcha harakatlarga tortishish maydoni o‘z ta’sirini ko‘rsatadi.
Faraz qilaylik, tog‘ cho‘qqisiga chiqib, undan gorizontal yo‘nalishda 0 tezlik bilan bironta jism uloqtirildi. Jism uchib borib, A nuqtaga tushadi. Unda uning ko‘rinishi Nyuton tomonidan chizilgan 2.3-rasmga o‘xshash bo‘ladi.
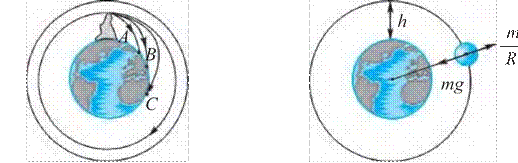
Jism tezligi oshirib borilsa, B va C nuqtalarga tushadi. Tezlikning ma’lum bir qiymatidan boshlab jism Yerga tushmasdan, Yer atrofi da aylana bo‘ylab harakatga keladi. Bu jism endi Yerning sun’iy yo‘ldoshi bo‘lib qoladi. Sun’iy yo‘ldoshning harakati, tortishish maydonidagi harakat bo‘ladi. Nima sababdan yo‘ldosh Yerga tushmaydi? Qanday tezlikda bu holat kuzatiladi? Avvalo, yo‘ldoshga ta’sir etayotgan kuchlarni olib qaraylik. Yo‘ldoshga doimo Yerning tortish kuchi ta’sir etadi. Bundan tashqari, unga havoning qarshilik kuchi ta’sir qiladi. Qarshilik kuchi kam bo‘lishi uchun uni atmosferaning eng yuqori qatlamlariga olib chiqish kerak.
2.3-rasm. 2.4-rasm.
Amalda Yer yuzasidan 300–400 km balandlikda havoning qarshiligi deyarli yo‘q. Demak, bunday balandlikda Yerning tortish kuchini yo‘ldoshiga berilgan tezlik tufayli vujudga kelgan markazdan qochma kuch kompensasiyalaydi (2.4- rasm). U holda:
 dan 2 = g (RYer + h).
dan 2 = g (RYer + h).
h balandlikni Yer radiusi Ryer ga nisbatan hisobga olmasa ham bo‘ladigan hol uchun Ryer + h ≈ Ryer va
![]() (2.5)
(2.5)
Uni hisoblash uchun Ryer ≈ 6400 km, g = 9,8 m/s2 deb olinsa, ning qiymati:
= 7,91 km/s ga teng bo‘ladi.
Bu tezlik birinchi kosmik tezlik deyiladi.
Shunday tezlik bilan harakatlangan Yerning sun’iy yo‘ldoshi
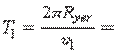 84 min 12 s da Yer atrofi ni bir marta
aylanib chiqadi.
84 min 12 s da Yer atrofi ni bir marta
aylanib chiqadi.
Amalda bir marta aylanib chiqish uchun ketgan vaqt hisoblab chiqilgan vaqtdan katta bo‘ladi. Bunga sabab yo‘ldosh orbitasining radiusi bilan Yer radiusining bir-biridan farq qilishidir.
Shunday qilib katta radiusli orbitalarda harakatlanadigan yo‘ldoshlarning tezligi Yer sirtiga yaqin orbitalarda harakatlanadigan yo‘ldoshlarning tezligidan kichik bo‘ladi.
Bunday yo‘ldoshlarning aylanish davri:
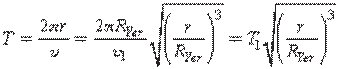 . (2.6)
. (2.6)
Bunda: T1 – Yer sirtiga yaqin orbitalarda harakatlanadigan yo‘ldoshlarn ing aylanish davri.
Istalgan balandlikda aylanayotgan yo‘ldoshning aylanish davri formulasidan foydalanib sun’iy yo‘ldosh Yerdan ma’lum balandlikdagi bir nuqtada “qimirlamasdan” turishi kerak bo‘lgan balandlikni topish mumkin. Demak, yo‘ldoshning aylanish davri 24 soatga teng bo‘lishi uchun qanday balandlikda harakatlanishi kerak? Hisoblashlar shuni ko‘rsatadiki, balandlik
h = 6,6 RYer ya’ni taxminan 42000 km ga teng bo‘lishi kerak!
Bunday orbita geostatsionar orbita deyiladi.
Bizning sayyoramizda insoniyat tarixida birinchi marta sobiq SSSRda 1957-yil 4-oktabrda Yerning sun’iy yo‘ldoshi uchirildi. Yo‘ldosh shar shaklida bo‘lib, diametri 58 sm, massasi 83,6 kg edi. Yo‘ldosh yer atrofi ni 1400 marta aylanib chiqib, umumiy holda 60 million km masofani bosib o‘tdi. 1961yil 12-aprelda inson birinchi marta kosmosga chiqdi. Birinchi kosmonavt Yuriy Alekseyevich Gagarin sobiq SSSR fuqarosi edi. Keyinchalik, 1969yil 20-iyulda amerikalik astronavtlar Neyl Armstrong va Edvin Oldrinlar birinchi bo‘lib Oyga qo‘nishdi.
Quyosh sistemasiga kiruvchi sayyoralarga borish uchun kosmik kemaga ikkinchi kosmik tezlik berilishi kerak. Uning son qiymati 11,2 km/s ga teng.
Olis yulduzlarga borish uchun esa Quyosh sistemasining tortish kuchini yengib chiqib ketish kerak. Buning uchun kosmik kema uchinchi kosmik tezlikka ega bo‘lishi kerak. Uning qiymati 16,7 km/s ga teng.
Kosmosni zabt etgan fazogirlar orasida bizning vatandoshlarimiz V. Jonibekov va o‘zbek millatiga mansub S. Sharipov ham bor.
1.
![]() Nima sababdan Yer, o‘zining atrofi da harakatlanayotgan
sun’iy yo‘ldoshni tortib olmaydi?
Nima sababdan Yer, o‘zining atrofi da harakatlanayotgan
sun’iy yo‘ldoshni tortib olmaydi?
2. Oyni ham birinchi kosmik tezlik bilan harakatlanayotgan yo‘ldosh deb qarash mumkinmi?
3. Sun’iy yo‘ldoshning yer yuzidan balandligi ortishi bilan uning tezligi qanday o‘zgaradi?
![]()
Hozirgi kunda ko‘pgina ma’muriy binolar, turarjoylar ko‘p qavatli qilib qurilgan. Yuqori qavatlarga chiqish va tushish uchun liftlardan foydalaniladi. Liftda chiqayotgan va tushayotgan odam harakatini qaraylik.
1.
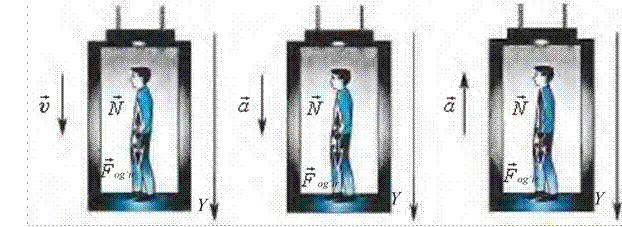
Massasi m bo‘lgan odam liftda turibdi. Lift pastga yoki
yuqoriga o‘zgarmas ![]() = const tezlik bilan harakatlanayotgan
holda (2.5-a rasm.) odamning lift poliga (tayanchga) beradigan ta’siri
(og‘irligi) P = mg bo‘ladi.
= const tezlik bilan harakatlanayotgan
holda (2.5-a rasm.) odamning lift poliga (tayanchga) beradigan ta’siri
(og‘irligi) P = mg bo‘ladi.
Boshqacha aytganda, lift o‘zgarmas tezlik bilan harakatlanganda jism og‘irligi lift tinch holatda turganda qanday bo‘lsa, shundayligicha qoladi.
a) b) d)
2. 5-rasm.
2. Lift pastga ![]() tezlanish bilan tushmoqda (2.5-b
rasm.). U holda Nyutonning ikkinchi qonuniga ko‘ra
tezlanish bilan tushmoqda (2.5-b
rasm.). U holda Nyutonning ikkinchi qonuniga ko‘ra
![]() +
m = m . (2.7)
+
m = m . (2.7)
Bunda ![]() – lift polining
reaksiya kuchi, m – jism massasi.
– lift polining
reaksiya kuchi, m – jism massasi.
![]() Nyutonning
uchinchi qonuniga ko‘ra jism og‘irligi = – . Shunga ko‘ra (2.7) ni
hisobga olib yozamiz
Nyutonning
uchinchi qonuniga ko‘ra jism og‘irligi = – . Shunga ko‘ra (2.7) ni
hisobga olib yozamiz
![]() .
.
Jismning harakat paytidagi natijaviy og‘irligi
![]() (2.8)
bo‘ladi.
(2.8)
bo‘ladi.
Bundan ko‘rinadiki, lift pastga tomon α tezlanish bilan harakatlansa, odamning og‘irligi ma ga kamayar ekan. Agar liftni ushlab turuvchi tros keskin bo‘shatilsa, lift pastga tomon a = g tezlanish bilan harakatlanadi va odamning og‘irligi
P = m(g – a) = 0 bo‘ladi.
Jismning tayanchga yoki osmaga ko‘rsatadigan kuchi nolga teng bo‘lad igan, ya’ni og‘irligi yo‘qoladigan holatga vaznsizlik deyiladi.
Demak, jism vaznsizlik holatiga o‘tishi uchun pastga tomon g = 9,81 m/s2 tezlanish bilan harakatlanishi kerak. Bundan jismlar erkin tushayotganda vaznsizlik holatida bo‘lishi kelib chiqadi. Qisman vaznsizlik holati arg‘imchoq uchayotganda, sakrashning tushish qismida, qiyalikdan inersiyasi bilan sakragan mototsiklchida kuzatiladi. Bu juda qisqa vaqt davom etadi. Yerning sun’iy yo‘ldoshlarida, orbital stansiyalarda istiqomat qiluvchi kosmonavtlar uzoq muddat vaznsizlik holatida bo‘ladi. Bunday paytda inson organizmida qon aylanishi va oziqlanish tizimi buziladi. Orbital stansiyalarda vaznsizlik holatining zararli oqibatlarini tugatish uchun maxsus choralar ko‘riladi.
3. Lift yuqoriga tomon ![]() tezlanish bilan
ko‘tarilmoqda (2.5-d rasm). Bunda odamning lift poli (tayanch)ga
ko‘rsatadigan og‘irligi
tezlanish bilan
ko‘tarilmoqda (2.5-d rasm). Bunda odamning lift poli (tayanch)ga
ko‘rsatadigan og‘irligi
![]()
![]() (2.9) ga teng bo‘ladi.
(2.9) ga teng bo‘ladi.
Bundan ko‘rinadiki, lift yuqoriga tomon tezlanish bilan ko‘tarilsa, odamning og‘irligi ma qiymatga ortadi. Bu holatga ortiqcha yuklama deyiladi.
Yuklamani, jismning harakat davridagi og‘irligining, tinch holatdagi og‘irligiga nisbati bilan topiladi:
n
= 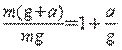 . (2.10)
. (2.10)
Bu holatda to‘la yuklama tayanchga tushadi. Lekin odam gavdasi bo‘ylab qisman yuklanishlar hosil bo‘ladi. Masalan, odam boshining og‘irligi uning bo‘yniga, bosh, bo‘yin, yelka va qo‘llarning og‘irligi esa belga va h. k. oyoqlarga tushadi. Agar liftning tezlanishi 0,3 – 1 m/s2 atrofi da bo‘lsa, inson uni sezmaydi. Lekin tovushdan tez uchuvchi samolyotlarda, raketaning ko‘tarilishida tezlanish 100 m/s2 gacha boradi. Bu holatga tushgan uchuvchilar va kosmonavtlarning aytishicha, og‘irlik ularni o‘rindiqqa mahkamlab tashlaydi, qo‘llarni ko‘tarish juda og‘irlik qiladi, qovoqni ko‘tarib, ko‘zni ochish haddan tashqari mashaqqatli bo‘ladi.
Masala yechish namunasi
Lift pastga qarab 4,5 m/s2 tezlanish bilan tushmoqda. Undagi jism og‘irligi necha marta kamayadi?
 .
.
1.
![]() Samolyotdan sakragan parashutchi: a) parashut
ochilgunga qadar erkin tushishda; b) parashut ochilgan lahzada; d) parashutda
bir
Samolyotdan sakragan parashutchi: a) parashut
ochilgunga qadar erkin tushishda; b) parashut ochilgan lahzada; d) parashutda
bir
tekisda tushayotgan paytida qanday holatda bo‘ladi?
2. Agar yuqoriga ko‘tarilayotgan yoki tushayotgan lift tormozlana boshlasa, undagi odam qanday holatda bo‘ladi?
3. Jism gorizontal yo‘nalishda tezlanuvchan harakatlansa, uning og‘irligi o‘zgaradimi?
![]()
Nyutonning ikkinchi qonunini o‘rganishda jismga faqat bitta kuch ta’sir etayotgan hol ko‘rib chiqilgan edi. Nyutonning uchinchi qonunini o‘rganishda jismlar ta’sirlashganda bir nechta kuchlar o‘zaro ta’sirlashishini ko‘rdik.
Kundalik turmushda ham jismga faqat bitta kuch ta’sir etadigan hol kuzatilmaydi. Harakatlanayotgan jismlarga tortuvchi kuchdan tashqari ishqalanish kuchi ham ta’sir qiladi. Gorizontal sirtda turgan m massali jismga Ft tortuvchi kuch ta’sir qilayotgan bo‘lsin. Bu paytda unga Fish ishqalanish kuchi ham ta’sir qiladi. Agar Ft > Fish bo‘lsa, jism harakatga keladi. Bunda jismning olgan tezlanishini aniqlash uchun qaysi kuchdan foydalanamiz? Bunda teng ta’sir etuvchi kuch tushunchasidan foydalaniladi. Teng ta’sir etuvchi kuch deyilganda jismga qo‘yilgan barcha kuchlarning geometrik yig‘indisi, ya’ni natijaviy kuch tushuniladi. Mazkur holda
![]() =
t + ishq. bo‘ladi.
=
t + ishq. bo‘ladi.
Tortuvchi kuch va ishqalanish kuchlarining vektor yig‘indisini koordinata o‘qlariga proyeksiyalar bilan almashtirib, algebraik yig‘indisi olinadi. U holda jismga ta’sir etuvchi kuchlar o‘zaro qarama-qarshi yo‘nalganligidan uning moduli
F = Ft – Fish bilan aniqlanadi.
Jismning olgan tezlanishi Nyutonning ikkinchi qonuniga ko‘ra
 (2.11)
bilan aniqlanadi.
(2.11)
bilan aniqlanadi.
Jismga bir nechta kuchlar ta’sir etadigan hol uchun ikkita masalani ko‘rib chiqaylik.
![]()
![]() 1. Qiya
tekislikka qo‘yilgan jismning muvozanat sharti va tushish tezlan ishini
qaraylik (2.6-rasm). Bun da α – qiya tekislikning qiyalak burchagi.
Qiya tekislik bilan unga qo‘yilg an taxtacha orasidagi ishqalanish koeffi
tsiyenti μ ga teng.
1. Qiya
tekislikka qo‘yilgan jismning muvozanat sharti va tushish tezlan ishini
qaraylik (2.6-rasm). Bun da α – qiya tekislikning qiyalak burchagi.
Qiya tekislik bilan unga qo‘yilg an taxtacha orasidagi ishqalanish koeffi
tsiyenti μ ga teng.
![]() Qiya tekislikda turgan
taxtachaga og‘irlik kuchi m, normal reaksiya
kuchi N→
va qiya tekislik bo‘ylab yuqoriga yo‘nalgan tinch holatdagi ishqalanish kuchi
Qiya tekislikda turgan
taxtachaga og‘irlik kuchi m, normal reaksiya
kuchi N→
va qiya tekislik bo‘ylab yuqoriga yo‘nalgan tinch holatdagi ishqalanish kuchi
ishq. ta’sir qiladi. 2.6-rasm x o‘qini qiya tekislik bo‘ylab pastga
yo‘naltiramiz, y – o‘qini tekislikka perpendikulyar yo‘naltiramiz.
Qiya
tekislikda jism muvozanatda qolishi uchun unga ta’sir qiluvchi kuchlarning teng
ta’sir etuvchisi nolga teng bo‘lishi kerak: mg→ + N→ + ![]() ishq. = 0.
ishq. = 0.
Bundan koordinata o‘qlariga bo‘lgan proyeksiyalar uchun tenglamalar sistemasini yozaylik:
1) x o‘qi
yo‘nalishi bo‘yicha mg sinα – ![]() ishq. = 0; 2) y o‘qi
yo‘nalishi bo‘yicha – mg cosα + N = 0.
ishq. = 0; 2) y o‘qi
yo‘nalishi bo‘yicha – mg cosα + N = 0.
Jism qiya tekislikda muvozanatda qolishi uchun ![]() ishq. ≥ mg
· sinα tengsizlik bajarilishi kerak.
ishq. ≥ mg
· sinα tengsizlik bajarilishi kerak.
Birinchi tenglamaga ko‘ra ![]() = mg · sinα, N
ikkinchi tenglamaga ko‘ra N = mg · cosα bo‘ladi. Bu
ifodalarni
= mg · sinα, N
ikkinchi tenglamaga ko‘ra N = mg · cosα bo‘ladi. Bu
ifodalarni ![]() ishq. = μ N tenglikni hisobga
olsak, mg sinα ≤ μmg cosα
tengsizlik bajariladi. Bundan tgα ≤ μ kelib chiqadi.
ishq. = μ N tenglikni hisobga
olsak, mg sinα ≤ μmg cosα
tengsizlik bajariladi. Bundan tgα ≤ μ kelib chiqadi.
Shunday qilib, tgα ≤ μ shart bajarilganda taxtacha qiya tekislikda muvozanatda qoladi.
Agar tgα ≥ μ bo‘lsa, jism qiya tekislik bo‘ylab pastga qarab tezlanish bilan harakatlanadi. Tezlanishni topish uchun ma = mg · sinα – μmg · cosα tenglamani tuzamiz. Tenglikning ikkala tomonini m ga qisqartirib,
![]() a = g (sinα – μcosα) (2.12) ga ega bo‘lamiz.
a = g (sinα – μcosα) (2.12) ga ega bo‘lamiz.
2. Massasi hisobga olinmas darajada kichik bo‘lgan ko‘chmas blokka m1 va m2 massali yuklar osilgan (2.7-rasm). Agar m2 > m1 bo‘lsa, yuklarning harakatlanish tezlanishi va ipning tarangligi topilsin. Blokdagi ishqalanish kuchi va ipning massasi hisobga olinmasin.
![]() Har bitta yukka ikkita kuch ta’sir qiladi: og‘irlik kuchi
va ipning taranglik kuchi.
Har bitta yukka ikkita kuch ta’sir qiladi: og‘irlik kuchi
va ipning taranglik kuchi.
Blokning va ipning massasi hamda ishqala nishni hisobga olmaslik haqidagi talab shuni anglatadiki, ipning har ikkala tomondagi tarang ligi bir xil bo‘ladi. Uni T bilan belgilab olamiz.
Yuklar uchun Nyutonning ikkinchi qonuni tenglamasini yozib olamiz:
mIp cho‘zilmas bo‘lganligidan, yuklarn ing ko‘chish
moduli va shunga muvofi q, tezlik va tezlanishlari 2.7-rasm. teng bo‘ladi. Yuklarning tezlanish modulini a bilan
belgilaymiz. U holda y o‘qini pastga yo‘naltirib, unga bo‘lgan proyeksiyalar uchun tenglamalar sistemasini yozamiz:
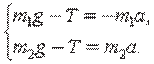
Ikkinchi tenglamadan birinchi tenglamani ayiramiz g (m2 – m1) = a (m2 + m1).
Bundan
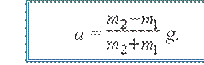 (2.13)
(2.13)
Birinchi tenglamadan ikkinchi tenglamani ayirib T = m1(g + a) ni, ikkinchidan birinchini ayirib, T = m2(g – a) ni hosil qilamiz. Bu – tezlanish bilan biri pastga, ikkinchisi yuqoriga harakatlanayotgan jismlarning og‘irligi. Yuklar tezlanish bilan harakatlanayotganligi sababli massalari turlicha bo‘lsa-da, og‘irliklari bir xil bo‘ladi. Tezlanish uchun topilgan ifodani ipning istalgan tomoni uchun yozilgan ifodasiga qo‘ysak,
![]() (2.14) ga ega bo‘lamiz. Shu ifoda bilan
har bir yukning o‘g‘irligi topiladi.
(2.14) ga ega bo‘lamiz. Shu ifoda bilan
har bir yukning o‘g‘irligi topiladi.
(2.15)
![]() 1. Jismga qo‘yilgan teng ta’sir
etuvchi kuch qanday aniqlanadi?
1. Jismga qo‘yilgan teng ta’sir
etuvchi kuch qanday aniqlanadi?
2. Kuchlarning koordinata o‘qlaridagi proyeksiyalari bilan ishlash, vektorlarni qo‘shishga nisbatan qanday afzalliklarga ega?
3. Jismga bir nechta kuch ta’sir qilganda uning muvozanatda bo‘lish sharti qanday aniqlanadi?
4. Blokdagi iplarga osilgan yuklarning og‘irligi harakat davrida nega teng bo‘lib qoladi?
2-mashq
1. Uyning tomi gorizontga nisbatan 30o ni tashkil etadi. Tom ustida yurgan odam oyoq kiyimining tagcharmi bilan tom usti orasidagi ishqalanish koeffi tsiyenti qancha bo‘lganda, u sirpanmasdan yura oladi? (Javobi: 0,58).
2. Qo‘zg‘almas blok orqali o‘tkazilgan arqonning uchlariga 50 g va 75 g li yuklar osilgan. Arqon va blok massasi hisobga olinmaydigan darajada kichik. Arqonni cho‘zilmas deb olib, yuklarning harakatlanish tezlanishini va arqonning taranglik kuchini toping. (Javobi: 1,96 m/s2; 0,6 N).
3. Arava ustida suyuqlik quyilgan idish qo‘yilgan. Arava gorizontal yo‘nalishda a tezlanish bilan harakatlanmoqda. Suyuqlik sirti barqaror holatda bo‘lganida, gorizont bilan qanday burchak tashkil qiladi? (Javobi: α = tgα).
4. O‘zgarmas kuch ta’sirida harakat boshlagan jism birinchi sekundda 0,5 m yo‘l bosdi. Agar jismning massasi 25 kg bo‘lsa, ta’sir etuvchi kuch nimaga teng? (Javobi: 25 N).
5. O‘zgarmas kuch ta’sirida harakat boshlagan 50 g massali jism 2 sekundda 1 m yo‘l bosdi. Ta’sir etuvchi kuch nimaga teng? (Javobi: 0,025 N).
6. Liftdagi suv solingan chelakda jism suzib yuribdi. Agar lift yuqoriga (pastga) a tezlanish bilan harakatlansa, jismning botish chuqurligi o‘zgaradimi?
7. Massasi M bo‘lgan silindrga ip o‘ralgan. So‘ngra silindrni pastga tashlab yuborilib, ipni yuqoriga tortib turiladi. Bunda silindrning massa markazi ipning yoyilishi davrida aynan bir xil balandlikda qoldi. Ipning taranglik kuchi nimaga teng.
8. Gorizontal joylashgan taxtachada yuk turibdi. Yuk va taxtacha orasidagi ishqalanish koeffi tsiyenti 0,1. Taxtachaga gorizontal yo‘nalishda qanday α tezlanish berilsa, uning ustidagi yuk sirpanib tushadi? (Javobi: 1 kg).
9. Qog‘oz varaq ustida to‘g‘ri silindr turibdi. Silindr balandligi 20 sm va asosining diametri 2 sm. Qog‘ozni qanday minimal tezlanish bilan tortilsa, silindr ag‘darilib tushadi. (Javobi: a = 0,1 m/s2).
10. Massasi 6 t bo‘lgan, yuk ortilmagan avtomobil 0,6 m/s2 tezlanish bilan harakatlana boshladi. Agar u o‘sha tortish kuchida joyidan 0,4 m/s2 tezlanish bilan qo‘zg‘alsa, unga ortilgan yukning massasi qancha bo‘lgan? (Javobi: 3 t).
1. Gapni to‘ldiring. Tinch holatda turgan yoki to‘g‘ri chiziqli tekis harakatlanayotgan sanoq sistemalari ... deyiladi.
A) ... nisbiy sanoq sistemalari; B) ... inersial sanoq sistemalari;
C) ... noinersial sanoq sistemalari; D) ... absolyut sanoq sistemalari.
2. Massasi 10 kg bo‘lgan jism 20 N kuch ta’sirida qanday harakat qiladi?
A) 2 m/s tezlik bilan tekis;
B) 2 m/s2 tezlanish bilan tezlanuvchan; C) 2 m/s2 tezlanish bilan sekinlanuvchan;
D) 20 m/s tezlik bilan tekis.
3. 1 m/s2 tezlanish bilan yuqoriga ko‘tarilayotgan liftda 50 kg mass ali odam turibdi. Odamning og‘irligi qanchaga teng (N)?
A) 50; B) 500; C) 450; D) 550.
4. Qo‘zg‘almas blokka arqon orqali massalari m1 va m2 bo‘lgan yuklar osilgan. Ular qanday tezlanish bilan harakatlanadi? m1 < m2 deb olinsin.
A) a = ![]() g;
B) a =
g;
B) a = 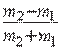 g; C) a =
g; C) a = 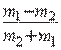 g;
D) a = 0.
g;
D) a = 0.
5. Liftning qanday harakatida undagi jismda yuklama vujudga keladi?
A) Yuqoriga o‘zgarmas tezlik bilan;
B) Pastga o‘zgarmas tezlik bilan;C) Yuqoriga o‘zgarmas tezlanish bilan;
D) Lift harakatsiz bo‘lganda.
6. Yo‘ldoshning geostatsionar orbitasi deyilganda nima tushuniladi?
A) Yo‘ldoshning Yer sirtidan minimal orbitasi;
B) Yo‘ldoshning Yer sirtidan maksimal orbitasi;
C) Yo‘ldoshning Yer sirtidan ma’lum balandlikda siljimasdan turish orbitasi;
D) Yo‘ldoshda kosmonavtlar kuzatuvlar olib boradigan orbita.
7. Dinamometr uchlariga ikkita 60 N dan bo‘lgan qarama-qarshi kuchlar qo‘yilsa, dinamometr necha nyutonni ko‘rsatadi?
A) 15; B) 30; C) 60; D) 120.
8. 3 N va 4N kuchlar bir nuqtada qo‘yilgan. Kuch yo‘nalishlari orasidagi burchak 90°. Teng ta’sir etuvchi kuch moduli qanday (N)?
A) 1; B) 5; C) 7; D) 1.
|
Dinamikaning birinchi qonuniga Galiley bergan ta’rif |
Agar jismga boshqa hech qanday jismlar ta’sir etmasa, jism Yerga nisbatan o‘zining tinch holatini yoki to‘g‘ri chiziqli tekis harakatni saqlaydi. |
|
Dinamikaning birinchi qonuni |
Inersial sistema deb ataluvchi shunday sanoq sistemalari mavjudki, undagi jism boshqa jismlardan yetarli darajada uzoq joylashgan bo‘lsa, tinch yoki to‘g‘ri chiziqli tekis harakatda bo‘ladi. |
|
Kuch |
Jismlarning bir-biriga ta’siri natijasida tezlanish olishga sabab bo‘ladigan miqdoriy o‘lchamga. |
|
Inert massa |
Jismga tegishli |
|
Dinamikaning ikkinchi qonuni |
|
|
Dinamikaning uchinchi qonuni |
Ta’sir har doim aks ta’sirini vujudga keltiradi. Ular son qiymati jihatidan bir-biriga teng bo‘lib, bir to‘g‘ri chiziq bo‘ylab qarama-qarshi yo‘nalgan: |
|
Inersial sanoq sistemalari |
Nisbatan tinch holatda turgan yoki to‘g‘ri chiziqli tekis harakatlanayotgan sanoq sistemalari. |
|
Noinersial sanoq sistemalari |
Egri chiziqli yoki tezlanish bilan harakatlanayotgan sanoq sistemalar. |
|
Inersiya kuchi |
Sanoq sistemasi tezlanish bilan harakatlanishi tufayli hosil bo‘lgan kuch. |
|
Birinchi kosmik tezlik |
Yerning sun’iy yo‘ldoshi bo‘lib qolishi uchun jism ega bo‘lishi kerak bo‘lgan tezlik – 7,91 km/s. |
|
Ikkinchi kosmik tezlik |
Quyosh sistemasiga kiruvchi sayyoralarga borish uchun kerak bo‘ladigan tezlik – 11,2 km/s. |
|
Uchinchi kosmik tezlik |
Quyosh sistemasining tortish kuchini yengib chiqib ketish uchun kerak bo‘ladigan tezlik – 16, 7 km/s. |
|
a→ tezlanish bilan vertikal harakatlanayotgan jism og‘irligi |
P→ = m ( – ) – pastga tushayotgan jism og‘irligi.
|
|
Vaznsizlik |
Jismning tayanchga yoki osmaga ko‘rsatadigan kuchi nolga teng bo‘ladigan, ya’ni og‘irligi yo‘qoladigan holat. |
|
Yuklama |
|
![]()
14-mavzu. ENERGIYA VA ISH. ENERGIYANING SAQLANISH QONUNI. JISMNING QIYA TEKISLIK BO‘YLAB
![]() Energiya – turli shakldagi harakatlar va o‘zaro
ta’sirlarning miqdoriy o‘lchovidir (u grekcha energeia – ta’sir so‘zidan
olingan). Energiya tabiatdagi harakatlarning shakliga qarab, turlicha bo‘ladi.
Masalan, mexanik, issiqlik, elektromagnit, yadro energiyalari va hokazolar.
O‘zaro ta’sir natijasida bir turdagi energiya boshqasiga aylanadi. Lekin bu
jarayonlarning barchasida, birinchi jismdan ikkinchisiga berilgan energiya
(qanday shaklda bo‘lishidan qat’iy nazar) ikkinchi jism birinchisidan olgan
energiyaga teng bo‘ladi. Nyutonning ikkinchi qonunidan ma’lumki, jismning
mexanik harakatini o‘zgartirish uchun unga boshqa jismlar tomonidan ta’sir
bo‘lmog‘i kerak. Boshqacha aytganda, bu jismlar o‘rtasida energiyalar almashuvi
ro‘y beradi. Mexanikada 3.1-rasm.
Energiya – turli shakldagi harakatlar va o‘zaro
ta’sirlarning miqdoriy o‘lchovidir (u grekcha energeia – ta’sir so‘zidan
olingan). Energiya tabiatdagi harakatlarning shakliga qarab, turlicha bo‘ladi.
Masalan, mexanik, issiqlik, elektromagnit, yadro energiyalari va hokazolar.
O‘zaro ta’sir natijasida bir turdagi energiya boshqasiga aylanadi. Lekin bu
jarayonlarning barchasida, birinchi jismdan ikkinchisiga berilgan energiya
(qanday shaklda bo‘lishidan qat’iy nazar) ikkinchi jism birinchisidan olgan
energiyaga teng bo‘ladi. Nyutonning ikkinchi qonunidan ma’lumki, jismning
mexanik harakatini o‘zgartirish uchun unga boshqa jismlar tomonidan ta’sir
bo‘lmog‘i kerak. Boshqacha aytganda, bu jismlar o‘rtasida energiyalar almashuvi
ro‘y beradi. Mexanikada 3.1-rasm.
ana shunday energiya almashuvini tavsifl ash
uchun mexanik ish tushunchasi kiritilgan va u fi zikada A harfi bilan belgilanadi.
Mexanik ish. Kuchning shu kuch ta’siri yo‘nalishida ro‘y bergan ko‘chishga skalyar ko‘paytmasiga teng bo‘lgan kattalik mexanik ish deyiladi, ya’ni
A = (F→ · s→) = F ·s · cosα. (3.1)
Bu yerda: α – kuch va ko‘chish s→ orasidagi burchak (3.1-rasm).
![]() Agar
; Fs
= F · cosα ekanligini e’tiborga olsak, (3.1) quyidagi
ko‘rinishni oladi:
Agar
; Fs
= F · cosα ekanligini e’tiborga olsak, (3.1) quyidagi
ko‘rinishni oladi:
![]() A = F · s · cosα
= Fs
· s. (3.2) bu yerda Fs – kuchning ko‘chish yo‘nalishiga proyeksiyasi.
A = F · s · cosα
= Fs
· s. (3.2) bu yerda Fs – kuchning ko‘chish yo‘nalishiga proyeksiyasi.
(3.2) ifodaga asoslanib, quyidagicha xulosa chiqarish mumkin: agar α < 2 bo‘lsa, 0 < cosα < 1 – kuchning ishi musbat, kuch va ko‘chish yo‘nalishi mos keladi; agar α > 2 bo‘lsa, –1< cosα < 0 – kuchning ishi manfi y, kuch va ko‘chish
yo‘nalishi qarama-qarshi bo‘ladi; agar α = 2 bo‘lsa, cos 90° = 0 bo‘lib, kuchning bajargan ishi nolga teng,
kuch ko‘chish yo‘nalishiga tik bo‘ladi.
Ish additiv (additiv – lotincha yig‘indi) kattalikdir (fi zikada additiv so‘zi – sistemadagi fi zik kattalik umumiy holda yaxlit hisoblanib, u shu kattalikni tashkil etuvchi qismlarning yig‘indisidan iborat degan ma’noni anglatadi).
Agar jismga bir nechta kuch ta’sir etayotgan bo‘lsa,
Fs = Fs1+ Fs2+ Fs3+…+ Fsn
bo‘ladi, unda to‘la ish, bu kuchlarning teng ta’sir etuvchisi bajaradigan ishga tengdir.
A = Fs · [∆s] = Fs1· [∆s1] + Fs2· [∆s2] + Fs3· [∆s3] + …+ Fsn[∆sn] yoki
A = A1+ A2+ A3+…+ An.
Ishning birligi. Ishning SI dagi birligi Joul (J):
[A] = [F] · [s] = 1 N · 1 m = 1 N · m = 1 J. (3.3)
Ishning SI dagi birligi sifatida 1 N kuchning jismni 1 m masofaga ko‘chirishda bajargan ishi qabul qilingan.
Og‘irlik kuchining ishi. Yer sirtida yaqin balandl iklarda jismga Yer tomonidan P = mg og‘irlik kuchi ta‘sir etadi. Yer sirtidan h balandlikdagi B nuqtadan Yer sathidan hisoblangan h2 balandlikdagi C nuqtaga o‘tishda jismning ko‘chishi h1 = h – h2 ga teng (3.2-rasm). Bunda og‘irlik kuchining bajargan ishi quyidagicha ifodalanadi:
A = Ph1 = mg(h – h2) = mgh – mgh2. (3.4)
![]() Bu yerda: P – jismning og‘irligi, m – uning
massasi, g – erkin tushish tezlanishi, h – vertikal bo‘ylab, h1 va h2 sathlar orasidagi
masofa.
Bu yerda: P – jismning og‘irligi, m – uning
massasi, g – erkin tushish tezlanishi, h – vertikal bo‘ylab, h1 va h2 sathlar orasidagi
masofa.
Og‘irlik kuchining bajargan ishi yo‘lning shakliga bog‘liq bo‘lmasdan, faqat tushish balandligiga bog‘liq. Shuning uchun ham og‘irlik kuchi ta’sirida bajariladigan ishlar trayektoriya shakliga emas, balki jismning boshlang‘ich va oxirgi holatiga bog‘liq. Bunday kuchlarga potensial yoki konservativ kuchlar deyiladi. Bu 3.2-rasm. kuchlarning maydoni esa potensial maydon deyiladi.
Jism pastga harakatlanganda og‘irlik kuchi va ko‘chish yo‘nalishi mos tushganligi sababli bajarilgan ish musbat, yuqoriga harakatlanganda esa, ular qarama-qarshi yo‘nalganligidan manfi y bo‘ladi. Shuning uchun og‘irlik kuchi ta‘sirida jism ko‘chib, yana boshlang‘ich vaziyatiga qaytgan holatdagi umumiy ish nolga teng bo‘ladi.
![]() Sistemaning
to‘la mexanik energiyasi deb, uning kinetik va potensial energiyalarining
yig‘indisiga aytiladi. Masalan Yer sirtidan h balandlikda Yerga
nisbatan
tezlik bilan harakatlanayotgan m massali jismning to‘la mexanik
energiyasi
Sistemaning
to‘la mexanik energiyasi deb, uning kinetik va potensial energiyalarining
yig‘indisiga aytiladi. Masalan Yer sirtidan h balandlikda Yerga
nisbatan
tezlik bilan harakatlanayotgan m massali jismning to‘la mexanik
energiyasi
E
= Ek
+ EP
=![]() + mgh. (3.4)
+ mgh. (3.4)
To‘la mexanik energiya jismlarning o‘zaro ta’siri vaqt o‘tishi bilan o‘zgarmaydi:
![]() E = Ek + EP = const. (3.5)
E = Ek + EP = const. (3.5)
Bunda mexanik energiyaning saqlanish qonuni deyiladi.
O‘tkazilgan ko‘plab tajribalar, nazariy xulosalar energiya saqlanish qonunining qat’iy bajarilishini ko‘rsatadi. Faqatgina tabiatda energiyaning bir turdan boshqasiga (masalan, mexanik energiyadan issiqlik energiyasiga) aylanishi ro‘y beradi. Shuning uchun ham bu qonunga energiyaning saqlanish va aylanish qonuni ham deyiladi. U tabiatning asosiy qonunlaridan bo‘lib, nafaqat makroskopik, balki mikrojismlar sistemasi uchun ham o‘rinlidir.
![]() Energiya hech
qachon yo‘qolmaydi ham, yo‘qdan paydo bo‘lmaydi ham u faqat bir turdan boshqa
turga aylanishi mumkin.
Energiya hech
qachon yo‘qolmaydi ham, yo‘qdan paydo bo‘lmaydi ham u faqat bir turdan boshqa
turga aylanishi mumkin.
Yopiq sistemada to‘la energiya saqlanadi.
Misol uchun, h balandlikdan tushayotgan jismning potensial energiyasi uning og‘irlik kuchiga bog‘liq bo‘lib, tajriba qaysi vaqtda o‘tkazilishiga mutlaqo bog‘liq emas.
Foydali ish koeffi tsiyenti. Mashina va dvigatellarning o‘ziga sarfl anayotgan energiyaning qancha qismi foydali ishga aylanishini ko‘rsatadigan kattalik kiritilgan.
Foydali ishning to‘la ishga nisbati foydali ish koeffi tsiyenti (FIK) deb ataladi va η harfi bilan belgilanadi.
Agar foydali ishni Af, to‘la ishni At bilan belgilasak, u holda FIK formulasi quyidagicha yoziladi:
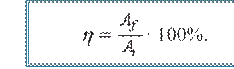 (3.6)
(3.6)
FIK birdan (100% dan) katta bo‘lmaydi. Mashina va dvigatellarda ishqalanish kuchining ishi tufayli to‘liq energiyaning bir qismi isrof bo‘ladi va shu sababli FIK har doim birdan kichik bo‘ladi.
Qiya tekislik va jism yuqoriga tortilganda bajarilgan ishni ko‘rib chiqaylik. Mexanikaning oltin qoidasiga muvofi q kuchdan necha marta yutilsa, yo‘ldan shuncha marta yutqiziladi.
Qiya tekislik ham ishdan yutuq bermaydi. Qiyalik burchagini kamaytirib yukni ko‘tarishga sarfl anadigan kuchdan yutiladi. Lekin ko‘chish masofasi ortganligi sababli bajarilgan ish o‘zgarmaydi.
![]() Uzunligi l, balandligi h bo‘lgan qiyalikda
og‘irligi P bo‘lgan yuqoriga harakatlanayotgan jismni qaraylik (3.3-
Uzunligi l, balandligi h bo‘lgan qiyalikda
og‘irligi P bo‘lgan yuqoriga harakatlanayotgan jismni qaraylik (3.3-
h rasm). Bunda jismga Fish ishqlanish kuchi, qiya tekislikka parallel bo‘lgan Ft yuqoriga tortuvchi kuch, qiya tekislikka
3.3-rasm perpendikulyar yo‘nalgan P┴ kuch va
tekislikka perpendikulyar kuchga qarama-qarshi tomonga yo‘nalgan N kuch (tekislikning reaksiya kuchi) ta‘sir etadi.
Agar ishqalanish kuchi hisobga olinmasa,
As = A1 = mgh (3.7) ga teng bo‘ladi. Lekin ishqalanish hisobga olinsa,
At = A1 + A2 (3.8) va
A2 = Fish · l = μN
· l = μmg · cosα ·![]() = μmg · ctgα (3.9)
bo‘ladi. Unda At
quyidagi ko‘rinishni oladi:
= μmg · ctgα (3.9)
bo‘ladi. Unda At
quyidagi ko‘rinishni oladi:
At = mgh + μmgh · ctgα = mgh(1 + μ · ctgα). (3.10)
Foydali ish koeffi tsiyenti:
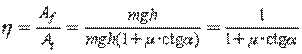 . (3.11)
. (3.11)
Yukka ta’sir etadigan tortish kuchi
![]() . (3.12)
. (3.12)
![]() 1. Mexanik ish qanday aniqlanadi?
1. Mexanik ish qanday aniqlanadi?
2. Og‘irlik kuchining ishi nimaga teng?
3. Tabiatda energiyaning saqlanish qonuni har doim bajariladimi?
4. Qiya tekislik ishdan yutuq beradimi?
![]()
Ishning maqsadi: Qiya tekislik va undan nima maqsadda foydalanilishini o‘rganish. Dinamometrda jismlar vaznini o‘lchash ko‘nikmasini shakllantirish. Foydali va to‘la ish hamda foydali ish koeffi tsiyenti haqidagi bilimlarni amalda mustahkamlash. Xatoliklarni hisoblash ko‘nikmalarini shakllantirish.
Kеrakli asboblar: uzun yupqa taxta, qisqichli shtativ, yog‘och brusok, yuklar to‘plami, dinamomеtr.
Ishning bajarilishi:
1) ![]() yupqa
taxta shtativga mahkam-
yupqa
taxta shtativga mahkam-
lanadi. So‘ngra qiya tеkislikning uzunligi l va balandligi h o‘lchab olinadi;
2) dinamomеtr yordamida yog‘och brusokning vazni P aniqlanadi;
3) brusokni qiya tеkislikka qo‘yib,
3.4-rasm. dinamomеtr yordamida qiya tеkislik
bo‘ylab F kuch bilan yuqoriga qarab bir
tеkisda (siltashsiz) tortiladi;
4) At = F · l yordamida to‘la, Af = P · h yordamida foydali ishlar hisoblanadi.
5)
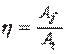 ifoda yordamida qiya tеkislikning foydali
ish koeffi tsiyеnti hisoblanadi.
ifoda yordamida qiya tеkislikning foydali
ish koeffi tsiyеnti hisoblanadi.
Tajriba kamida uch marta takrorlanadi va natijalar quyidagi jadvalga yoziladi.
|
№ |
l, (m) |
h, (m) |
F, (N) |
P, (N) |
At, (J) |
Af, (J) |
η, (%) |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
Tajribani turli xil qiya tеkisliklar (turli xil h balandliklar) uchun o‘tkazib, foydali ish koeffi tsiyеntining qiya tеkislik burchagiga bog‘liqligi haqida xulosalar chiqariladi.
1.
![]() Qiya tеkislik qanday qurilma va u qanday maqsadda
ishlatiladi?
Qiya tеkislik qanday qurilma va u qanday maqsadda
ishlatiladi?
2. Foydali va to‘la ishlar qanday aniqlanadi?
3. Foydali ishning to‘la ishdan kam bo‘lishiga sabab nima?
4. Foydali ish koeffi tsiyеntining qiya tеkislik burchagiga bog‘liql igini qanday tushuntirasiz?
![]()
To‘qnashish deb, ikki yoki undan ko‘p jismlarning juda qisqa vaqt davomidagi ta’sirlashuviga aytiladi.
To‘qnashish tabiatda juda ko‘p uchraydi. Bilyard sharlarining to‘qnashuvi, odamning yerga sakrashi, bolg‘acha bilan mixning qoqilishi, futbolchining to‘p tepishi va hokazolar to‘qnashishga misol bo‘ladi.
To‘qnashish natijasida jismlarning deformatsiyalanishiga qarab ular ikki turga: absolyut elastik va absolyut noelastik to‘qnashishlarga bo‘linadi.
Absolyut noelastik to‘qnashish. Absolyut noelastik to‘qnashish deb, ikkita deform atsiyalanadigan sharlarning to‘qnashib, birga yoki bir xil tezlik bilan harakatlanishiga aytiladi. To‘qnas huvdan so‘ng sharlar birlashib, harakat qilishi mumkin. Plastilin yoki loydan yasalgan sharchalarning to‘qnashuvi bunga misol bo‘la oladi (3.5-rasm).
m1
![]()
 2 m1 →1 m2 →2
2 m1 →1 m2 →2
|
|
m1 |
m →' 2 |
→'2 |
![]()
![]() 1
1
3.5-rasm. 3.6-rasm.
m1
massali jismning to‘qnashishdan oldingi tezligi ![]() 1, m2 massali jismning
to‘qnashishdan oldingi tezligi →
1, m2 massali jismning
to‘qnashishdan oldingi tezligi → ![]() 2 bo‘lsin. To‘qnashishdan keyingi tezl ik bo‘lsa, impulsning saqlanish
qonunini tatbiq etib quyidagini olamiz:
2 bo‘lsin. To‘qnashishdan keyingi tezl ik bo‘lsa, impulsning saqlanish
qonunini tatbiq etib quyidagini olamiz:
![]()
Bundan
(3.13)
Absolyut noelastik to‘qnashishda mexanik energiyaning saqlanish qonuni bajarilmay, uning bir qismi sharlarning ichki energiyasiga aylanadi.
Absolyut elastik to‘qnashish deb, ikkita deform atsiyalanmaydigan sharlarning to‘qnashishiga aytiladi. Bunda sharlarn ing to‘qnashishdan oldingi kinetik energiyalari, to‘qnashishdan keyin ham to‘laligicha kinetik energiyaga aylanadi.
Absolyut elastik to‘qnashishda impulsning va kinetik energiyaning saqlanish qonunlari bajariladi. m1 va m2 massali sharlarning to‘qnashishgacha tezliklari mos ravishda
→ → → →
1 va 2, to‘qnashishdan keyin esa '1 va '2 bo‘lsin. Ularning harakat yo‘nalishlarini hisobga olib o‘ng tomonga yo‘nalgan harakatni musbat, chap tomonga yo‘nalganini esa manfi y ishora bilan olamiz (3.6-rasm). Shu hol uchun impulsning va kinetik energiyaning saqlanish qonunlari quyidagicha bo‘ladi:
![]() (3.14)
(3.14)
Yuqoridagi formulalarni birgalikda yechib, '1 va '2 tezliklarni topish mumkin:
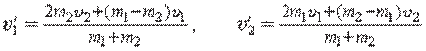 . (3.15)
. (3.15)
![]() 1. Absolyut noelastik to‘qnashish
deb qanday to‘qnashishga aytiladi?
1. Absolyut noelastik to‘qnashish
deb qanday to‘qnashishga aytiladi?
2.Absolyut noelastik to‘qnashishda energiyaning saqlanish qonuni bajariladimi?
3.Absolyut elastik to‘qnashish deb qanday to‘qnashishga aytiladi?
Masala yechish namunasi
O‘zgarmas F kuch ta’sirida vagon 5 m yo‘lni bosib o‘tdi va 2 m/s tezlik oldi. Agar vagonning massasi 400 kg va ishqalanish koeffi tsiyenti 0,01 bo‘lsa, kuch bajargan A ish aniqlansin.
![]()
![]() Y e c h i l i s h i:
Y e c h i l i s h i:
Kuchning bajargan ish: A, vagonni ko‘chirishdagi ish A0 ga va unga kinetik energiya Ek berish uchun bajarilgan ishlarning yig‘indisiga teng
A = A0 + Ek.
Bu yerda: Fishq = μP. P = mg ekanligini e’tiborga olsak, A0 = Fish ·s = μmgs. O‘z navbatida, vagon olgan kinetik energiya
Ek = ![]()
Shunday qilib, F kuch bajargan ish A = μmgs+. Berilganlardan foydalanib
A = 0,01 · 400 · 9,8 · 5 J + ![]() · 400
· 4 J = 996 J.
· 400
· 4 J = 996 J.
Javobi: A=996 J.
3-mashq
1. 0,3 m/s tezlik bilan harakatlanayotgan 20 t massali vagon 0,2 m/s tezlik bilan harakatlanayotgan 30 t massali vagonni quvib yetadi. Agar to‘qnashish noelastik bo‘lsa, ular o‘zaro urilgandan keyin vagonlarning tezligi qanday bo‘ladi? (Javobi: = 0,24 m/s).
2. Odam massasi 2 kg bo‘lgan jismni 1 m balandlikka 3 m/s2 tezlanish bilan ko‘targanda qancha ish bajaradi? (Javobi: A = 26 J).
3. Massasi 6,6 t bo‘lgan kosmik kema orbita bo‘ylab 7,8 m/s tezlik bilan harakatlanayotgan bo‘lsa, uning kinetik energiyasi nimaga teng bo‘ladi? (Javobi: Ek = 200 GJ).
4. 5 m balandlikdan erkin tushayotgan 3 kg massali jismning yer sirtidan 2 m balandlikdagi potensial va kinetik energiyalari nimaga teng? (Javobi: Ep=60 J; Ek=90 J).
5.
Koptokni yerdan qaytib 2h balandlikka ko‘tarilishi uchun uni
h balandlikdan pastga qanday boshlang‘ich tezlik 0 bilan tashlash kerak? To‘qnashish
absolyut elastik deb hisoblansin. (Javobi: 0 = ![]() ).
).
6. Massasi 1 kg bo‘lgan moddiy nuqta aylana bo‘ylab 10 m/s tezlik bilan tekis harakatlanmoqda. Davrning to‘rtdan bir ulushida, davrning yarmida, butun davrda impulsning o‘zgarishini toping. (Javobi: 14 kg·m/s; 20 kg·m/s; 0).
7. Massasi 0,5 kg bo‘lgan jism 4 m/s tezlikda yuqoriga vertikal otildi. Jism maksimal balandlikka ko‘tarilishida og‘irlik kuchining ishini, potensial energiyasining va kinetik energiyasining o‘zgarishini toping. (Javobi: 4 J;
4 J; – 4 J).
8. Massalari 1 kg va 2 kg bo‘lgan noelastik sharlar bir-biriga tomon, mos ravishda, 1 va 2 m/s tezlik bilan harakatlanmoqda. To‘qnashgandan keyin sistema kinetik energiyasining o‘zgarishini toping (Javobi: 3 J).
9. Massasi 15 t bo‘lgan trolleybus joyidan 1,4 m/s2 tezlanish bilan qo‘zg‘aldi. Qarshilik koeffi tsiyenti 0,02. Dastlabki 10 m yo‘lda tortish kuchi bajargan ishni va qarshilik kuchi bajargan ishni toping. Bunda trolleybus qancha kinetik energiya olgan? (Javobi: 240 kJ, – 30 kJ, 210 kJ).
10. Chana balandligi 2 m va asosi 5 m bo‘lgan tepalikdan tushadi va tepalik asosidan 35 m gorizontal yo‘lni bosib o‘tib to‘xtaydi. Ishqalanishni butun yo‘l davomida bir xil deb hisoblab, ishqalanish koeffi tsiyentini toping. Shunga o‘xshash usul bilan tajribada, masalan, gugurt qutisi va chizg‘ich orasidagi ishqalanish koeffi tsiyentini toping. (Javobi: 0,05).
1. ... turli shakldagi harakatlar va o‘zaro ta’sirlarning miqdoriy o‘lchovidir. Gapni to‘ldiring.
A) Energiya; B) Potensial energiya;
C) Kinetik energiya; D) Elektr energiya.
2. Energiyaning SI dagi birligi nima?
A) Vatt; B) Joul; C) Kaloriya; D) N · m.
3. … kuchning shu kuch ta’sirida ro‘y bergan ko‘chishga skalyar ko‘paytmasiga teng bo‘lgan kattalik. Gapni to‘ldiring.
A) Energiya; B) Potensial energiya;
C) Kinetik energiya; D) Mexanik ish.
4. Energiya hech qachon yo‘qolmaydi ham, yo‘qdan paydo bo‘lmaydi ham u faqat bir turdan boshqasiga aylanishi mumkin. Bu nimaning ta’rifi ?
A) Nyutonning birinchi qonuni; B) Nyutonning ikkinchi qonuni;
C) Energiyaning saqlanish qonuni; D) Nyutonning uchinchi qonuni.
5. Foydali ishning to‘la ishga nisbati nimani anglatadi?
A) Energiyani; B) Potensial energiyani;
C) Kinetik energiyani; D) FIKni.
6. Sistemaning … deb, uning kinetik va potensial energiyalarining yig‘indisiga aytiladi Gapni to‘ldiring.
A) ... energiyasi; B) ... to‘la mexanik energiyasi;
C) ... kinetik energiyasi; D) ... mexanik ishi.
7. … to‘qnashish deb, ikki yoki undan ko‘p jismlarning juda qisqa vaqt davomidagi ta’sirlashuviga aytiladi. Gapni to‘ldiring.
A) Absolyut elasti; B) Absolyut noelastik;
C) To‘qnashish; D) Ko‘chish.
8. … to‘qnashish deb, ikkita deformatsiyalanadigan sharlarning to‘qnashishiga aytiladi. Gapni to‘ldiring.
A) Absolyut elastik; B) Absolyut noelastik;
C) To‘qnashish; D) Ko‘chish.
9. ... to‘qnashish deb, ikkita deformatsiyalanmaydigan sharlarning to‘qnashishiga aytiladi. Gapni to‘ldiring.
A) Absolyut elastik; B) Absolyut noelastik;
C) To‘qnashish; D) Ko‘chish.
10. Jismning boshlang‘ich va oxirgi holatiga bog‘liq bo‘ladigan kuchlarga … kuchlar deyiladi. Nuqtalar o‘rniga to‘g‘ri javobni qo‘ying.
A) ... og‘irlik; B) ... musbat;
C) ... potensial yoki konservativ; D) ... manfi y.
|
Energiya |
Turli shakldagi harakatlar va o‘zaro ta’sirlarning miqdoriy o‘lchovi. Uning SI dagi birligi 1 J. |
|
Mexanik ish |
Kuchning shu kuch ta’sirida ro‘y bergan ko‘chishga skalyar ko‘paytmasiga teng bo‘lgan kattalik. A = F · s · cosα. |
|
Sistemaning to‘la mexanik energiyasi |
Sistemaning kinetik va potensial energiyalarining yig‘indisi. |
|
Energiyaning saqlanash qonuni |
Energiya hech qachon yo‘qolmaydi ham, yo‘qdan paydo bo‘lmaydi ham, u faqat bir turdan boshqasiga aylanadi. |
|
Foydali ish koeffi tsiyenti |
Foydali ishning to‘la ishga nisbati: |
|
To‘qnashish |
Ikki yoki undan ko‘p jismlarning juda qisqa vaqt davomidagi ta’sirlashuvi. |
|
Absolyut elastik to‘qnashish |
Ikkita deformatsiyalanmaydigan sharlarning to‘qnashishi. |
|
Absolyut noelastik to‘qnashish |
Ikkita deformatsiyalanadigan sharlarning to‘qnashib, birga yoki bir xil tezlik bilan harakatlanishi. |
![]()
Uyning shiftiga osilgan qandil misolida qo‘yilgan kuchlarni qaraylik (4.1rasm).
![]() Buning uchun, avvalo, 6-sinfda o‘rganilgan jismlarning
massa markazi haqidagi tushunchani eslaylik. Massa markazi deyilganda
jismning barcha massasi mujassam bo‘lgan xayoliy nuqta tushuniladi.
Buning uchun, avvalo, 6-sinfda o‘rganilgan jismlarning
massa markazi haqidagi tushunchani eslaylik. Massa markazi deyilganda
jismning barcha massasi mujassam bo‘lgan xayoliy nuqta tushuniladi.
Shunga ko‘ra jismga ta’sir etayotgan kuchlarni massa
markaziga nisbatan olamiz. Osib qo‘yilgan lampaga pastga yo‘nalgan og‘irlik
kuchi ![]() ta’sir qiladi. Natijada uni tutib
turuvchi ip tarang bo‘lib tortiladi. Ipda hosil bo‘lgan 4.1-rasm. taranglik
kuchi
ta’sir qiladi. Natijada uni tutib
turuvchi ip tarang bo‘lib tortiladi. Ipda hosil bo‘lgan 4.1-rasm. taranglik
kuchi ![]() va og‘irlik kuchi
va og‘irlik kuchi ![]() massa
markazidan o‘tuvchi to‘g‘ri chiziqda yotadi va yo‘nalishi jihatidan
qarama-qarshi bo‘ladi. Bu kuchlar son qiymati jihatidan teng bo‘ladi. Bu
kuchlarni vektorlarni qo‘shish qoidasiga binoan qo‘shilsa, natijaviy kuch nolga
teng bo‘ladi. Shunga ko‘ra lampa muvozanatda qo‘ladi.
massa
markazidan o‘tuvchi to‘g‘ri chiziqda yotadi va yo‘nalishi jihatidan
qarama-qarshi bo‘ladi. Bu kuchlar son qiymati jihatidan teng bo‘ladi. Bu
kuchlarni vektorlarni qo‘shish qoidasiga binoan qo‘shilsa, natijaviy kuch nolga
teng bo‘ladi. Shunga ko‘ra lampa muvozanatda qo‘ladi.
Biror-bir jism qiya tekislikda muvozanatda turgan holni ko‘raylik (4.2rasm). Bunda jismga qo‘yilgan kuchlarni massa markaziga nisbatan qaraylik. Jismga avvalo og‘irlik kuchi mg→ ta’sir qiladi.
![]() Bu kuchni
Bu kuchni ![]() 1 va F→2 tashkil etuvchilarga
ajrataylik.
1 va F→2 tashkil etuvchilarga
ajrataylik.
Bunda F→1 kuch jismni qiya tekislik bo‘ylab → pastga sirpantirishga harakat qiladi. F2-kuch qiya tekislik yuzasiga beradigan bosim kuchini hosil qiladi. Bu kuch yuza tomonidan jismga reaksiya 4.2-rasm.
kuchi N→ hosil bo‘lishiga olib keladi. Jism sirpanishiga qarama-qarshi yo‘nalishda ishqalanish kuchi F→3 ta’sir qiladi.
Bu holda ham jismga ta’sir etayotgan barcha kuchlarning vektor yig‘indisi nolga teng bo‘ladi.
F→1 + F→2 + N→1 + F→3 = 0.
Yuqoridagilardan kelib chiqib quyidagi xulosani chiqarish mumkin:
![]() Aylanish o‘qiga
ega bo‘lmagan jism yoki jismlar sistemasi muvozanatda qolishi uchun unga ta’sir
etayotgan kuchlarning vektor yig‘indisi nolga teng bo‘lishi kerak.
Aylanish o‘qiga
ega bo‘lmagan jism yoki jismlar sistemasi muvozanatda qolishi uchun unga ta’sir
etayotgan kuchlarning vektor yig‘indisi nolga teng bo‘lishi kerak.
F→1 + F→2 + F→3 + ..... + F→n = 0.
Muvozanat turlari.

4.3-rasm.
Agar biror jism muvozanatda turgan bo‘lsa, uni doimo shunday holatda qoladi deb bo‘lmaydi (4.3-rasm). Chunki real sharoitlarda unga tashqaridan tasodifi y turtkilar berilib turiladi. Bunday turtkilardan jismlarni to‘la xoli qilishning imkoni yo‘q. Muhimi shunday turtkilardan so‘ng jism muvozanatda qoladimi yoki muvozanat buziladimi shuni bilish kerak. Buning uchun tashqi turtki vositasida muvozanat vaziyatidan chetlashgan jismga ta’sir etuvchi natijaviy kuch yo‘nalishini aniqlash kerak. Hosil bo‘ladigan natijaviy kuch yo‘nalishiga ko‘ra muvozanat uch turda bo‘ladi.
1. Turg‘un muvozanat. Jismni muvozanat holatidan chetga chiqarilg anda, uni dastlabki vaziyatiga qaytaruvchi kuch hosil bo‘ladigan muvozanatga turg‘un muvozanat deyiladi (4.4-a rasm). Bunda yarim sfera ichiga qo‘yilgan sharcha muvozanat vaziyatidan chetlashtirilganda, unga ta’sir etayotgan kuchlarning teng ta’sir etuvchisi uni yana muvozanat holatiga qaytaradi.
2. Turg‘unmas muvozanat. Jismni muvozanat holatidan chetga chiqarilganda, uni dastlabki vaziyatidan uzoqlashtiruvchi kuch hosil bo‘ladigan muvozanatga turg‘unmas muvozanat deyiladi (4.4-b rasm). Bunda yarim sfera ustiga qo‘yilgan sharcha muvozanat vaziyatidan chetlashtirilganda, unga ta’sir etayotgan kuchlarning teng ta’sir etuvchisi uni muvozanat holatidan yanada chetlashtiradi.
m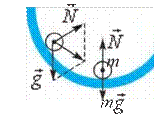
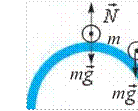
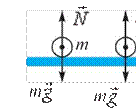
a) d)
4.4-rasm.
3. Farqsiz muvozanat. Jismni muvozanat holatidan chetga chiqarilganda, uning holatini o‘zgartiradigan hech qanday kuch hosil bo‘lmasa farqsiz muvozanat deyiladi (4.4-d rasm). Gorizontal sirt ustiga qo‘yilgan sharchaga tashqi turtki berilganda, joyidan siljiydi. Lekin unga ta’sir etayotgan kuchlarning teng ta’sir etuvchisi nolga teng bo‘ladi.
4. ![]() 5-rasmda
keltirilgan jismga o‘girlik markazidan quyida joylashgan B nuqtaga F1 kuch ta’sir
ettirilsa (F1
> Fishq.
· Fishq.
– ishqalanish kuchi), jism ilgarilanma
5-rasmda
keltirilgan jismga o‘girlik markazidan quyida joylashgan B nuqtaga F1 kuch ta’sir
ettirilsa (F1
> Fishq.
· Fishq.
– ishqalanish kuchi), jism ilgarilanma
harakatga keladi. Kuch kattaligini o‘zgartirmagan 1
holda uni A nuqtaga ko‘chirilsa, jism qiyshaya boshlaydi. Og‘irlik markazidan pastga yo‘nalgan G vektor bilan jism pastki asosi konturining chetki 4.5-rasm.
nuqtasi orasidagi masofa l kamaya boshlaydi. Kuch ta’sir ettirish davom etsa, G vektor jism asosini chegaralovchi kontur ichidan chiqadi va jism ag‘dariladi.
Shunday qilib jismning turg‘unligi (barqarorligi):
1) jism og‘irligiga;
2) jism asosi yuzining kattaligiga;
3) ag‘daruvchi kuchning og‘irlik markazidan qanchalik quyiga qo‘yilganligiga bog‘liq.
F1 = ![]() . (4.1)
. (4.1)
Masala yechish namunasi
1. Massasi 10 kg bo‘lgan jism ikkita cho‘zilmas arqonga osilgan. Ular o‘zaro 60° burchak hosil qilgan holda muvozanatda qoladi. Arqonlarning taranglik kuchlarini hisoblang.
![]()
![]()
![]() 1.
Jismlarning massa markazi joylashgan nuqta yo‘nalishida kuch ta’sir ettirilsa,
nima kuzatiladi?
1.
Jismlarning massa markazi joylashgan nuqta yo‘nalishida kuch ta’sir ettirilsa,
nima kuzatiladi?
2. Aylanish o‘qiga ega bo‘lmagan jismlarga ta’sir etayotgan kuchlar ning vektor yig‘indisi nolga teng bo‘lsa, nima kuzatiladi?
3. Muvozanat turlariga turmush va texnikadan misollar keltiring.
![]()
6-sinfda Siz oddiy mexanizmlardan richag, qo‘zg‘aluvchan va qo‘zg‘almas bloklar, chig‘iriq va lebyodka bilan tanishgansiz. Ularning ishlashiga e’tibor berilsa, barchasida aylanish o‘qlari mavjud bo‘ladi.
Bunday jismlarning muvozanatda bo‘lishi uchun ularga ta’sir etayotgan kuchlarning vektor yig‘indisi nolga teng bo‘lishi yetarli emasligi ham aytilgan edi. Bunda kuch qo‘yilgan nuqtaning, aylanish o‘qidan qanday uzoqlikda bo‘lishiga ham bog‘liq bo‘ladi.
Kuch qo‘yilgan nuqtadan, aylanish o‘qigacha bo‘lgan eng qisqa masofaga kuch yelkasi deb ataladi. Bunda, kuch va yelka har doim o‘zaro perpendikulyar bo‘ladi.
Kuchning kuch yelkasiga ko‘paytmasiga kuch momenti deyiladi:
M = F · l,
Kuch momenti birligi [M] = 1 N · m.
![]() Jism kuch momenti
ta’sirida aylanish o‘qi atrofi da buriladi. Bunda jismga ta’sir etayotgan kuch
momenti, juft kuch ta’siriga o‘xshash bo‘ladi. Juft kuch
deyilganda, yo‘nalishi qarama-qarshi, kattaliklari teng, lekin bir o‘qda
yotmaydigan kuchlar tushuniladi.
Jism kuch momenti
ta’sirida aylanish o‘qi atrofi da buriladi. Bunda jismga ta’sir etayotgan kuch
momenti, juft kuch ta’siriga o‘xshash bo‘ladi. Juft kuch
deyilganda, yo‘nalishi qarama-qarshi, kattaliklari teng, lekin bir o‘qda
yotmaydigan kuchlar tushuniladi.
Bunga misol tariqasida avtomobil rulining burilishini keltirish mumkin (4.6-rasm). 4.6-rasm. Aylanish o‘qi rulning o‘rtasida bo‘lib, unga juft F1 kuchlar ta’sir etadi.
Natijaviy kuch momenti rulni bir tomonga burovchi momentlarni o‘zaro qo‘shib topiladi:
М =
F1![]() = F1d1.
= F1d1.
![]() Agar aylanish o‘qiga ega bo‘lgan jismga bir nechta kuchlar
ta’sir etayotgan bo‘lsa, bu kuchlarning momentlarini o‘zaro qo‘shish orqali
natijaviy moment topiladi. Bunda jismni soat strelkasi yo‘nalishida
aylantiruvchi kuch momentlarini musbat ishorada, soat strelkasi yo‘nalishiga
qarama-qarshi yo‘nalishda aylantiruvchi kuch momentlarini manfi y ishorada
olinadi.
Agar aylanish o‘qiga ega bo‘lgan jismga bir nechta kuchlar
ta’sir etayotgan bo‘lsa, bu kuchlarning momentlarini o‘zaro qo‘shish orqali
natijaviy moment topiladi. Bunda jismni soat strelkasi yo‘nalishida
aylantiruvchi kuch momentlarini musbat ishorada, soat strelkasi yo‘nalishiga
qarama-qarshi yo‘nalishda aylantiruvchi kuch momentlarini manfi y ishorada
olinadi.
![]() 4.7-rasmda masshtabli
chizg‘ichning O nuqtasidan B l2 O l1 A shtativga osilib, undan turli uzoqlikda
qo‘yilgan yuklar keltirilgan. Bunda A nuqtaga osilgan yuklar og‘irligi
4.7-rasmda masshtabli
chizg‘ichning O nuqtasidan B l2 O l1 A shtativga osilib, undan turli uzoqlikda
qo‘yilgan yuklar keltirilgan. Bunda A nuqtaga osilgan yuklar og‘irligi
F1 ga, aylanish o‘qidan uzoqligi l1 ga teng bo‘lib chizg‘ichni soat strelkasi yo‘nalishida harakatlantiruvchi 4.7-rasm.
momentni hosil qiladi. В nuqtaga osilgan yuklar
og‘irligi F2 ga, aylanish o‘qidan uzoqligi l2 ga teng bo‘lib, chizg‘ichni soat strelkasi yo‘nalishiga qarama-qarshi yo‘nalishda aylantiruvchi kuch momenti hosil qiladi. Natijaviy kuch momentini topish uchun jismga ta’sir etuvchi kuch momentlarining ishorasini hisobga olib qo‘shamiz:
М = F2l2 + (– F1l1) = F2l2 – F2l2.
Bundan ko‘rinadiki, jism muvozanatda qolishi uchun M = 0 bo‘lishi kerak.
Shunga ko‘ra aylanish o‘qiga ega bo‘lgan jismlarning muvozanat sharti quyidagicha bo‘ladi:
![]() Aylanish o‘qiga
ega bo‘lgan jismga ta’sir etayotgan kuch momentlarining vektor yig‘indisi nolga
teng bo‘lganda jism muvozanatda qoladi:
Aylanish o‘qiga
ega bo‘lgan jismga ta’sir etayotgan kuch momentlarining vektor yig‘indisi nolga
teng bo‘lganda jism muvozanatda qoladi:
M→1 + M→2 + M→3 + ….. + M→n = 0. (4.2)
Bu qoida Arximed tomonidan topilgan bo‘lib, momentlar qoidasi deb yuritiladi. Momentlar qoidasiga asoslanib ishlaydigan oddiy mexanizmlarga richag, ko‘chmas va ko‘char bloklar, chig‘iriq, vint (domkrat) larning ishlash tamoyili momentlar qoidasiga asoslangandir.
Richag. Amaliyotda richagning uch turi ishlatiladi (4.8-rasm).
a) b) d)
4.8-rasm.
Ikki yelkali richagda (4.8-а rasm) tayanch richagning kuchlar qo‘yilgan nuqtalari oralig‘ida bo‘ladi.
Bir yelkali richagda (4.8-b rasm) tayanch richagning bir uchiga joylashtirilgan bo‘lib, yukni richagning ikkinchi uchiga qo‘yiladi. Tutib turuvchi kuchni tayanch va yuk qo‘yilgan nuqtalar oralig‘iga jo‘ylash tiriladi. Ularda kuchlar antiparallel yo‘nalgan bo‘ladi. Inson qo‘li, yong‘oq chaqadigan qisqich ularga misol bo‘la oladi (4.9-rasm).
Richagning uchinchi turida (4.8 d-rasm) tayanch richagning bir uchiga joylashtirilgan bo‘lib, yukni tayanch va tutib turuvchi kuch qo‘yilgan nuqtalar oralig‘iga qo‘yiladi. Ularda ham kuchlar antiparallel yo‘nalgan bo‘ladi. Zambilg‘altak, otashkurak ularga misol bo‘la oladi (4.10-rasm).
Bloklar. Turmush va texnikada bloklardan foydalan ishda ko‘char va ko‘chmas bloklar majmuasidan foydalaniladi. Majmuada bloklar o‘zaro ulanib, darajali polispast hosil qilinadi.
4.9-rasm. 4.10-rasm. 4.11-rasm.
4.11-rasmda mana shunday darajali polispast keltirilgan. Darajali polispastda osilgan yuk og‘irligi bloklarga o‘ralgan arqonlarga taqsimlanadi.
 (4.3)
(4.3)
Shunga ko‘ra polispastda yuk nechta arqonga taqsimlansa, yukni ko‘tarish uchun kerak bo‘ladigan kuch shuncha marta kam bo‘ladi.
![]() 1. Jismga
ta’sir etuvchi kuch momentlari qanday qoida asosida qo‘shiladi?
1. Jismga
ta’sir etuvchi kuch momentlari qanday qoida asosida qo‘shiladi?
2. Aylanish o‘qiga ega bo‘lgan jismning muvozanatiga doir misol lar keltiring.
3. Polistpastda ko‘chmas bloklar soni ortib borsa, uning kuchni orttirib berish kattaligi qanday o‘zgaradi?
![]()
19-mavzu. AYLANMA HARAKAT DINAMIKASI
Siz ko‘pgina jangari fi lmlarni tomosha qilganingizda, haydovchi avtomobil rulini keskin yon tomonga burganida mashina ag‘darilib ketganligini ko‘rgansiz. Sirkda motosiklchining devor bo‘ylab yurganligini ham ko‘rganlar bor.
Shunday tajriba o‘tkazib ko‘raylik. Chelak ichiga ozgina suv solib, uni vertikal tekislikda aylantiraylik. Chelak aylanish davomida yuqori nuqtadan o‘tayotganda chelakdagi suv to‘kilmasdan o‘tadi.
Yuqorida keltirilgan misollardan mashinani ag‘daruvchi, motosiklchini devorga siqib turuvchi va chelakdagi suv og‘irligini muvozanatlovchi kuch mavjudligi kelib chiqadi.
Bu kuch qanday hosil bo‘ladi va uning kattaligi nimalarga bog‘liq?
Buning uchun aylana bo‘ylab tekis harakat qilayotgan jismda markazga intilma kuch mavjud bo‘lishini eslaylik:
 (4.4)
(4.4)
Nyutonning uchinchi qonuniga ko‘ra:
Fm.i.k. = Fm.q.k
markazdan qochma kuch F→m.q.k. ham paydo bo‘ladi.
Mana shu markazdan qochma kuch keskin burilgan mashinani ag‘daradi va aylanayotgan chelakning to‘nkarilgan holatida suvning to‘kilishiga yo‘l qo‘ymaydi.
4.12-rasmda R radiusli aylana bo‘ylab harakatlanayotgan jismga ta’sir etuvchi kuchlar ko‘rsatilgan. Birinchi holatda
![]() F m.q.k markazdan
qochma kuch F→m.q.k. og‘irlik
F m.q.k markazdan
qochma kuch F→m.q.k. og‘irlik
kuchi mg→ ga qarama-qarshi yo‘nalganligi tufayli jism og‘irligi kamayadi:
P1 = mg – ![]() . (4.5)
. (4.5)
Uchinchi holatda jismning og‘irlik m.q.k kuchi va markazdan qochma kuch pastga,
4.12-rasm ya’ni bir tomonga yo‘nalgan. Shunga
ko‘ra, jism og‘irligi ortadi:
P2 = mg + ![]() .
(4.6)
.
(4.6)
Markazdan qochma kuchni aylanuvchi jismlarda hamda jism harakati davomida burilishi zarur bo‘lgan hollarda hisobga olinadi.
Xuddi shunday yo‘lning burulish qismlarida markazga intilma kuch ta’sirida vertikal holatdan og‘ish kuzatiladi. Bu holat avariyaga olib kelmasligi uchun velosipedchi yoki mototsiklchilar aylanish markazi tomon biroz og‘ib harakatlanishlari zarur (4.13 a-rasm). Avtomobilda bu kuchni muvozanatlash uchun yo‘lning bir tomonini biroz ko‘tarib quriladigan bo‘ldi (4.13 b-rasm). Tramvay va poyezdlarning relslari yo‘lning qayrilish joylarida tashqi aylanasi biroz ko‘tarilib quriladi.
![]() Fishq
Fishq 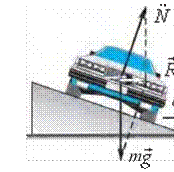
a) b)
4.13-rasm.
Masala yechish namunasi
Jism biror balandlikdan tushib, halqa bo‘ylab harakatlanadi. Halqaning radiusi qanday bo‘lganda jism halqaning T nuqtasidan tushib ketmaydi. Jismning T nuqtadagi tezligi 30 m/s.
![]()
![]() B e r i l g a n: Y
e c h i l i s h i:
B e r i l g a n: Y
e c h i l i s h i:
= 30 m/s Jism T nuqtadan tushib ketmasligi uchun Fog‘ir. = Fm.q.k g = 10 m/s2
_______________
Topish kerak;
R – ?
Javobi: 90 m.
![]() 1.
Markazdan qochma kuch ta’siriga asoslanib ishlaydigan qanday asboblarni
bilasiz?
1.
Markazdan qochma kuch ta’siriga asoslanib ishlaydigan qanday asboblarni
bilasiz?
2. Yo‘lning burilish qismlarida nima sababdan avtomobillarning yurish tezligi cheklanadi?
3. Mashina haydovchisi keskin burilish joyiga yaqinlashganda nima qilishi lozim? Nima uchun haydovchi namgarchilik bo‘lganda, yo‘lda to‘kilgan barglar ko‘p bo‘lgan vaqtda va yaxmalakda nihoyatda ehtiyot bo‘lishi kerak?
![]()
20-mavzu. SUYUQLIK VA GAZLAR HARAKATI,
OQIMNING UZLUKSIZLIK TEOREMASI.
Siz tinch holatda turgan suyuqlik va gazlarning idish devoriga bosim berishi haqida bilib olgansiz. Tabiatda va turmushda suyuqlik tinch holatdan tashqari, harakatda ham bo‘ladi. Ariq, kanal, daryolar va vodoprovod quvurlarida oqayotgan suvda qanday kuchlar vujudga keladi? Buni o‘rganish uchun ariqda oqayotgan suv yuzasi holatini bir eslab ko‘raylik. Suvi mo‘l, keng kanalda sekin oqayotgan suvning o‘rta qismi bir tekisda, taxminan bitta chiziq bo‘ylab, harakat qiladi. Buni suvda birga oqib kelayotgan cho‘plar harakatini kuzatib ishonch hosil qilish mumkin (4.14-rasm). Bunday oqim qatlamli yoki laminar oqim deyiladi. Tog‘dan tushib kelayotgan ariq suvi tez oqadi. Unga tashlangan mayda cho‘plar, barglar harakati kuzatilsa, ko‘pchilik joylarida girdob, ya’ni uyurma ko‘rinishidagi harakatlar hosil bo‘ladi (4.15-rasm.) Bunday oqimga turbulent oqim deyiladi. Demak, suyuqlik biror-bir nayda oqqanda suyuqlikning nay devorlariga ishqalanishi tufayli qatlamlarning siljishi nayning o‘rta qismida tezroq, chetki qismlarida sekinroq bo‘lar ekan.
Ishqalanishni hisobga olmagan holda, suyuqlikning ko‘ndalang kesim yuzasi o‘zgaradigan nay bo‘ylab oqishini qaraylik (4.16-rasm)
Suyuqlik nayning S1 yuzaga ega bo‘lgan qismiga 1 tezlik bilan kirib, S2 yuzali qismidan 2 tezlik bilanchiqib ketadi. Kichik bir Δt vaqt ichida S1 yuzadan m1 massali suyuqlik, S2 yuzadan m2 massali suyuqlik oqib o‘tadi. Massaning saqlanish qonuniga asosan m1 = m2. Massalar o‘rniga suyuqlik zichligi ρ va hajmi V orqali ifodasini qo‘ysak ρ1 S11Δt = ρ2 S22Δt.
Suyuqlikning siqilmasligi hisobga olinsa, ρ1 = ρ2 bo‘ladi. U holda
![]() S
S
S2
4.14-rasm. 4.15-rasm. 4.16-rasm.
S11Δt = S22Δt bo‘ladi. Tenglikning ikkala tomonini Δt ga bo‘lib yuborsak,
S11 = S22 (4.7) ga ega bo‘lamiz. Olingan natijani quyidagicha ta’rifl ash mumkin:
Turli kesim yuzali nayda oqayotgan siqilmas suyuqlik tezliklarining moduli, suyuqlik kesim yuzalariga teskari proporsional bo‘ladi. Bunga siqilmas suyuqlik uchun oqim uzluksizligi tenglamasi deyiladi.
Shunday qilib, oqim nayining keng qismida suyuqlik tezligi kichik, tor joyida esa katta bo‘ladi. Vodoprovod shlangidan suv sepayotganda suvni uzoqroqqa sepish uchun shlang uchi qisiladi.
![]() Harakatlanuvchi suyuqliklarda bosimning taqsimlanishini
qaraylik.
Harakatlanuvchi suyuqliklarda bosimning taqsimlanishini
qaraylik.
Tepa qismida ingichka o‘lchov naylari ulangan, turli yuzali nay bo‘ylab suyuqlik oqayotgan bo‘lsin (4.17-rasm). Suyuqlik statsionar oqimida har bir o‘lchov naylari bo‘ylab 4.17-rasm.
![]() suyuqlik ko‘tariladi.
Suyuqlik ustunlarining balandliklariga ko‘ra nayning devorlariga berayotgan
bosimi haqida fi kr yuritish mumkin. Tajribalar shuni ko‘rsatadiki nayning keng
qismidagi bosim, uning tor qismiga nisbatan katta bo‘ladi. Oqim uzluksizligi
tenglamasiga muvofi q nayning keng qismida oqim tezligi kichik, tor qismida
katta bo‘ladi. Bundan quyidagi xulosani olamiz:
suyuqlik ko‘tariladi.
Suyuqlik ustunlarining balandliklariga ko‘ra nayning devorlariga berayotgan
bosimi haqida fi kr yuritish mumkin. Tajribalar shuni ko‘rsatadiki nayning keng
qismidagi bosim, uning tor qismiga nisbatan katta bo‘ladi. Oqim uzluksizligi
tenglamasiga muvofi q nayning keng qismida oqim tezligi kichik, tor qismida
katta bo‘ladi. Bundan quyidagi xulosani olamiz:
Suyuqlikning oqim tezligi katta bo‘lgan joylarida uning bosimi kichik va aksincha oqim tezligi kichik bo‘lgan joylarida katta bo‘ladi.
Suyuqlik bosimining oqim tezligiga bog‘liqligining matematik ifodasini 1738-yilda D. Bernulli aniqlagan edi.
Bernulli tenglamasini suyuqlik oqimiga mexanik energiyaning saqlanish qonunini qo‘llab chiqarish mumkin.
![]() Suyuqlik oqayotgan
ko‘ndalang kesim B l1 yuzasi o‘zgaradigan
nayni gorizontga nisbatan qiya holda o‘rnataylik (4.18-rasm.)
Suyuqlik oqayotgan
ko‘ndalang kesim B l1 yuzasi o‘zgaradigan
nayni gorizontga nisbatan qiya holda o‘rnataylik (4.18-rasm.)
Nayning keng qismidagi AB yuzasidan boshlab ma’lum bir suyuqlik hajmini ajratib
qaraylik. Bu hajm oqib o‘tishi uchun t vaqt 2 kerak bo‘lsin. Suyuqlik siqilmas bo‘lganligidan shu vaqt davomida nayning tor qismidagi CD 4.18-rasm.
yuzasidan ham shuncha hajmdagi suyuqlik
oqib o‘tadi. Suyuqlikning AB yuzasini S1, undan oqib o‘tish tezligini 1 va CD yuzasini S2, undan oqib o‘tish tezligini 2 bilan belgilaylik. Bosim kuchlari F1 va F2 hamda ajratib olingan hajmdagi suyuqlik og‘irlik kuchi ta’sirida t vaqt davomida o‘ng tomonga siljiydi. Bunda bajarilgan ish
A = A1 + A2 = F1 l1 – F2l2 = p1 S11Δt + p2 S22Δt.
Suyuqlikning statsionar oqimida A1B1 va CD oraliqda (4.18-rasmda shtrixlangan yuza) gi suyuqlikning energiyasi o‘zgarmaydi, ya’ni ABB1A1 hajmni egallagan suyuqlik ko‘chib, CDD1C1 hajmni egallaydi. Energiyaning saqlanish qonuniga ko‘ra tashqi kuchlarning bajargan ishi energiya o‘zgarishiga teng:
ΔE = ΔEk + ΔEp = ![]() ρΔV
(22–21) + ρg (S2l2 h2 – S1
l1 h1).
ρΔV
(22–21) + ρg (S2l2 h2 – S1
l1 h1).
S2l2 = S1l1 = ΔV ekanligi hisobga olinib ΔV ga qisqartirilsa
![]()
![]() p1 + ρgh1 + ρ221 = p2 + ρgh2 + ρ222 . (4.8)
p1 + ρgh1 + ρ221 = p2 + ρgh2 + ρ222 . (4.8)
Bu ideal suyuqlik yoki gaz oqimi uchun Bernulli tenglamasi deyiladi.
Agar h1 = h2 bo‘lsa,
p1 + ![]() = p2 +
= p2 + ![]() bo‘ladi.
bo‘ladi.
Masala yechish namunasi
Tubida tiqin bilan berkitilgan, kichik tirqishi bo‘lgan idishga 1 m balandlikda suv quyilgan. Suv yuzasiga massasi 1 kg va yuzasi 100 sm2 bo‘lgan porshen qo‘yilgan. Idish devori va porshen oralig‘idan suv sizib o‘tmaydi. Tiqin olingan zahoti suv tirqishdan qanday tezlik bilan otilib chiqadi?
|
B e r i l g a n: |
Y e c h i l i s h i: |
|
m = 1 kg S = 100 sm2 |
Bernulli tenglamasidan foydalanamiz. Suv oqimining bosimi atmosfera bosimi po ga teng. Tirqishdan boshlab |
![]()
![]()
![]() h
= 1 mh balandlikdagi porshen tagidagi bosim po + ga teng. _______________
h
= 1 mh balandlikdagi porshen tagidagi bosim po + ga teng. _______________
Topish kerakBernulli tenglamasiga ko‘ra
= ?po + .
Bundan ≈ 4,9 m/s.
Javobi: 4,9 m/s.
1.
![]() Suyuqlikning dinamik bosimi deganda nimani tushunasiz?
Suyuqlikning dinamik bosimi deganda nimani tushunasiz?
2. Laminar va turbulent oqimlar qanday ta’rifl anadi?
3. O‘zingiz yashaydigan joyda oquvchi suvlar qanday ko‘rinishda oqishini ta’rifl ab bering.
4. Nima sababdan suyuqlik tezligi ortsa, uning bosimi kamayadi?
![]()
21-mavzu. HARAKATLANAYOTGAN GAZLAR VA
SUYUQLIKLARDA BOSIMNING TEZLIKKA
Suyuqlik tinch holatda turganiga nisbatan harakat holatida bosim o‘zgarishini ko‘rdik. Bu bosim dinamik bosimga bog‘liq deyiladi. Dinamik bosim suyuqlik yoki gazning tezligiga bog‘liq bo‘lishini kuzatish uchun quyidagicha tajriba o‘tkazaylik. Ikki varaq qog‘oz olib, tik holatda ushlaylik. So‘ngra qog‘oz orasiga pufl aylik (4.19-rasm). Shunda qog‘ozlar bir-biriga tomon intilib yaqinlashadi. Buning sababi shundaki, qog‘ozlar orasidagi havo pufl ash natijasida harakatga keladi va u joydagi bosim kamayadi. Qog‘ozlarning tashqi tomonidagi bosim, ichki qismidagidan katta bo‘lib qolganligi tufayli, qog‘ozlarni siquvchi kuch paydo bo‘ladi. Bir tomonga harakatlanayotgan ikkita kema ba’zan hech qanday sababsiz to‘qnashib ketganligi kuzatilgan. Buning sababini ham xuddi ikkita qog‘oz varag‘i orasiga pufl anganida bosimlar farqi hosil bo‘lishi bilan tushuntiriladi.
![]()
 p
p
4.20-rasm.
4.19-rasm.
1. Samolyot qanotini ko‘taruvchi kuch. Samolyotlarning parvozi ham aynan shu hodisani o‘rganish tufayli amalga oshirildi. Buni samolyot qanotining maxsus tuzilishi bilan tushuntiriladi (4.20-rasm).
![]() Samolyot qanoti “suyri” shaklida yasalib, unga kelib
urilayotgan shamol, qanotning ostki va ustki tomonidan o‘tadi. Ustki qismida
shamol o‘tishi kerak bo‘lgan yo‘l pastki qismidan ko‘proq. Shu sababli ustki
qismida shamol tezligi pastkisidan kattaroq bo‘lishi kerak. Demak, shamol
tezligi katta bo‘lgan joydagi bosim p1 shamol tezligi kichik bo‘lgan ostki qismidagi
bosim p2
dan kichik bo‘ladi. Natijada pastdan yuqoriga yo‘nalgan bosimlar farqi p = p2 – p1 hosil bo‘ladi.
Oqim turbulent bo‘lsa, bosimlar farqi katta bo‘ladi. Shu bosimlar farqi tufayli
samolyot qanotini ko‘taruvchi kuch hosil bo‘ladi. 2. Magnus effekti.
Futbol maydonida burchakdan tepilgan to‘pning burilib darvozaga
kirganini televizorda yoki stadionda kuzatganlar ko‘p. To‘pning burilishiga nima
majbur qiladi? Bunga sabab shuki, to‘pning o‘rtasiga emas, balki biroz
chetrog‘iga tepgan usta futbolchi uni to‘g‘ri harakati davomida aylanishiga
majbur qiladi.
Samolyot qanoti “suyri” shaklida yasalib, unga kelib
urilayotgan shamol, qanotning ostki va ustki tomonidan o‘tadi. Ustki qismida
shamol o‘tishi kerak bo‘lgan yo‘l pastki qismidan ko‘proq. Shu sababli ustki
qismida shamol tezligi pastkisidan kattaroq bo‘lishi kerak. Demak, shamol
tezligi katta bo‘lgan joydagi bosim p1 shamol tezligi kichik bo‘lgan ostki qismidagi
bosim p2
dan kichik bo‘ladi. Natijada pastdan yuqoriga yo‘nalgan bosimlar farqi p = p2 – p1 hosil bo‘ladi.
Oqim turbulent bo‘lsa, bosimlar farqi katta bo‘ladi. Shu bosimlar farqi tufayli
samolyot qanotini ko‘taruvchi kuch hosil bo‘ladi. 2. Magnus effekti.
Futbol maydonida burchakdan tepilgan to‘pning burilib darvozaga
kirganini televizorda yoki stadionda kuzatganlar ko‘p. To‘pning burilishiga nima
majbur qiladi? Bunga sabab shuki, to‘pning o‘rtasiga emas, balki biroz
chetrog‘iga tepgan usta futbolchi uni to‘g‘ri harakati davomida aylanishiga
majbur qiladi.
4.21-rasm. Natijada to‘pning chap va o‘ng tomonidagi havo oqimining tezligi o‘zgaradi va bosimlar farqi hosil bo‘lib, to‘pni darvoza tomonga buradi. Bunga Magnus effekti deyiladi (4.21-rasm).
3. Idishdagi tirqishdan otilib chiqayotgan suyuqlik tezligini hisoblash.
Bernulli tenglamasidan foydalanib, suyuqlik sirtidan h chuqurlikda bo‘lgan idish tirqishidan otilib chiqayotgan suyuqlik tezligini hisoblash mumkin (4.22-rasm).
![]() Idishdagi suyuqlikning ustki yuzasidagi bosim, atmosfera
bosimi po ga
teng. Suyuqlik tezligi 0 = 0. Suyuqlik
chiqadigan tirqish oldidagi bosim ham po ga teng. Tirqishdan chiquvchi suyuqlik
tezligini
bilan belgilab, bu ikkita joy uchun 4.9-formulani qo‘llaymiz:
Idishdagi suyuqlikning ustki yuzasidagi bosim, atmosfera
bosimi po ga
teng. Suyuqlik tezligi 0 = 0. Suyuqlik
chiqadigan tirqish oldidagi bosim ham po ga teng. Tirqishdan chiquvchi suyuqlik
tezligini
bilan belgilab, bu ikkita joy uchun 4.9-formulani qo‘llaymiz:
4. ![]() 22-rasm. po + = p + ρgh,
bundan
22-rasm. po + = p + ρgh,
bundan
. (4.10)
Bunga ideal suyuqlik uchun Torrichelli formulasi deyiladi.
Masala yechish namunasi
Bo‘yi 5 m bo‘lgan sisternada yerdan 50 sm balandlikda jo‘mrak o‘rnatilgan. Jo‘mrak ochilsa, undan suyuqlik qanday tezlik bilan otilib chiqadi?
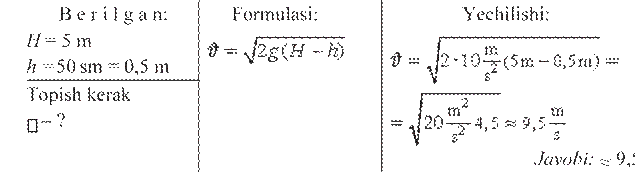
1.
![]() Uyda qog‘ozdan turli ko‘rinishdagi varrak yasang. Qaysi
varrakda ko‘taruvchi kuch katta bo‘lishini asoslashga urinib ko‘ring.
Uyda qog‘ozdan turli ko‘rinishdagi varrak yasang. Qaysi
varrakda ko‘taruvchi kuch katta bo‘lishini asoslashga urinib ko‘ring.
2. Jismoniy tarbiya darsida futbol to‘pini burchakdan tepib, burilishiga erishib ko‘ring.
![]() 1. Varrak qanday kuchlar ta’sirida
yuqoriga ko‘tariladi?
1. Varrak qanday kuchlar ta’sirida
yuqoriga ko‘tariladi?
2 4.22-rasmdagi idishdan otilib chiqayotgan suyuqlik tezligi tirqish yuzasiga bog‘liqmi?
3. Ko‘pgina avtomobillarning tashqi ko‘rinishini nega uchburchak, to‘rtburchak yoki shunga o‘xshash shaklda yasalmaydi?
4. Magnus effektidan yana qaysi joylarda foydalanish mumkin?
3-mashq
1. Arqonni osilmaydigan qilib tortish mumkinmi?
2. Massasi 1,2 · 103 kg bo‘lgan truba yerda yotibdi. Uning bir uchidan ko‘tarish uchun qanday kuch kerak? (Javobi: ≈ 6 · 103 N).
3. Massasi 1,35 t bo‘lgan avtomobil g‘ildiraklari o‘rnatilgan o‘qlar birbiridan 3 m uzoqlikda joylashgan. Avtomobilning massa markazi oldingi o‘qdan 1,2 m uzoqlikda joylashgan. Avtomobilning har bir o‘qiga qo‘yilgan kuchlarni aniqlang.
4. Kub shaklidagi jismni ag‘darish uchun uning ustki qirrasiga qanday kuch bilan ta’sir etish kerak? Bunda kubning polga ishqalanish koeffi tsiyentining minimal qiymati qanchaga teng bo‘lishi kerak? Kubning tomoni a ga, massasi M ga teng.
5. Asosi kvadratdan iborat bo‘lgan baland bo‘yli taxtacha gorizontal tekislikda turibdi. Faqat chizg‘ichdan foydalanib taxtacha va tekislik orasidagi ishqalanish koeffi tsiyentini qanday aniqlash mumkin?
6. Jismga kattaligi 100 N dan bo‘lgan uchta kuch ta’sir qilmoqda. Agar birinchi va ikkinchi kuchlar orasidagi burchak 60o, ikkinchi va uchinchi kuchlar orasidagi burchak 90o bo‘lsa, kuchlarning teng ta’sir etuvchisini toping. (Javobi: 150 N).
7. Uzunligi 10 m bo‘lgan kir quritish arqonida og‘irligi 20 N bo‘lgan kostum osilib turibdi. Kostum ilingan kiyim ilgich arqonning o‘rtasida bo‘lib, arqon mahkamlangan nuqtalardan o‘tgan gorizontal chiziqdan 10 sm pastda joylashgan. Arqonning taranglik kuchini toping. (Javobi: 500 N).
8.
![]() Vertikal devorga arqon bilan osib qo‘yilgan yashik
Vertikal devorga arqon bilan osib qo‘yilgan yashik
4.23-rasmda ko‘rsatilganidek qola oladimi?
9. Uzunligi 10 m, massasi 900 kg bo‘lgan rels ikkita parallel tross bilan ko‘tarilmoqda. Troslardan biri relsning uchiga, ikkinchisi boshqa uchidan 1 m narida joylashgan. Troslarning taranglik kuchlarini toping. (Javobi: 4 kN; 5 kN).
10. Bir jinsli og‘ir metall sterjen buklandi va bir uchidan 4.23-rasm.
erkin osib qo‘yildi. Agar bukilish burchagi 90o bo‘lsa, sterjenning osilgan uchi vertikal bilan qanday burchak tashkil qiladi? (Javobi: tgα = 1/3).
11. Daryo suvi uning qaysi joyida tez oqadi: suvning sirtqi qismidami yoki ma’lum bir chuqurlikdami; daryoning o‘rtasidami yoki qirg‘oqqa yaqin joyidami?
12. Suv keltirish tarmog‘i teshilib, undan tepaga suv otilib chiqa boshladi. Agar tirqish yuzasi 4 mm2, suvning otilib chiqish balandligi 80 sm bo‘lsa, bir sutkada qancha suv isrof bo‘ladi? (Javobi: 1380 l).
13. Suv osti kemasi 100 m chuqurlikda suzmoqda. O‘quv mashqi vaqtida unda kichik tirqish ochildi. Agar tirqishning diametri 2 sm bo‘lsa unga suv qanday tezlik bilan kiradi? Tirqish orqali bir soatda qancha suv kiradi? Kema ichidagi bosim atmosfera bosimiga teng. (Javobi: 44,3 m/s; 50 m3).
14. O‘t o‘chirish uchun ishlatiladigan suv quvuridagi suv sarfi 60 l/min. Agar quvurdan chiqqan suv yuzasi 1,5 sm2 bo‘lsa, 2 m balandlikda suv yuzasi qanchaga teng bo‘ladi?
15. Nima sababdan pishgan tuxumga qarab uzilgan o‘q uni teshib o‘tadi, lekin xom tuxumni parchalab yuboradi?
1. Massalari 2M, 3M va M bo‘lgan doira shaklidagi jismlar rasmda ko‘rsatilganidek o‘rnatilgan. Ularning og‘irlik markazi qaysi nuqtada joylashgan?
A) KL nuqtalar orasida;
B) ![]() L
nuqtasida; O
L
nuqtasida; O
C) M nuqtasida;
3M
D) LM nuqtalar orasida.
2. Rasmda keltirilgan sistema muvozanatda turibdi. F kuch R ning qancha qismiga teng.
A) ![]() 1/2;
1/2;
B) 1/4;
C) 1/8;F
D) 2.
3. Kuch yelkasi – bu….
A) richag uzunligi;
B) richagning aylanish o‘qidan oxirigacha bo‘lgan masofa;
C) kuch vektori yo‘nalishidan aylanish o‘qigacha bo‘lgan eng qisqa masofa;
D) richagga ta’sir etuvchi juft kuchlar orasidagi eng qisqa masofa.
4. Rasmda richagga ta’sir etuvchi F→1 va F→2 kuchlar keltirilgan. F→1 va F→2 kuchlarning yelkalarini ko‘rsating.
A) OA; OD; A B O C D
B)
![]() BD; СA;
BD; СA;
C) AB; СD;
D) OB; OС.
5. Rasmda keltirilgan richaglardan qaysi biri muvozanatda bo‘ladi?
A) Faqat 1; №1 №2
B) Faqat 2;
C) Faqat 3;
D) ![]() Faqat 1 va
3. 1 №3 2
Faqat 1 va
3. 1 №3 2
6. Kuch momenti qanday birlikda o‘lchanadi?
A) Nyuton metr (N · m); B) Joul (J);
С) Vatt sekund (W · s); D) Joul/sekund (J/s).
7. “Turli yuzali nayda oqayotgan siqilmas suyuqlik tezliklarining moduli, suyuqlik yuzalariga teskari proporsional bo‘ladi”. Bu tasdiqning nomi nima?
|
A) Oqim uzluksizligi tenglamasi; |
B) Torrichelli tenglamasi; |
|
C) Bernulli tenglamasi; 8. Torrichelli formulasini ko‘rsating. |
D) Magnus qoidasi. |
A) ![]()
![]() = ; B)
=
= ; B)
=
C) = ; 1 = const.
9. Bernulli tenglamasini ko‘rsating.
A) ![]()
![]() = ; B)
=
= ; B)
=
C) = ; 1 = const.
10. Bo‘yi 5 m bo‘lgan sisterna tagiga jo‘mrak o‘rnatilgan. Jo‘mrak ochilsa undan suyuqlik qanday tezlik bilan otilib chiqadi?
A) 9,5 m/s; B) 95 sm/s; C) 9,8 m/s; D) 10 m/s.
|
Turg‘un muvozanat |
Jismni muvozanat holatidan chetga chiqarilganda, uni dastlabki vaziyatiga qaytaruvchi kuch hosil bo‘ladigan muvozanat. |
|
Turg‘unmas muvozanat |
Jismni muvozanat holatidan chetga chiqarilganda, uni dastlabki vaziyatidan uzoqlashtiruvchi kuch hosil bo‘ladigan muvozanat. |
|
Farqsiz muvozanat |
Jismni muvozanat holatidan chetga chiqarilganda, uning holatini o‘zgartiradigan hech qanday kuch hosil bo‘lmaydigan muvozanat. |
|
Kuch momenti |
Kuchning kuch yelkasiga ko‘paytmasi: M = F · l |
|
Aylanish o‘qiga ega bo‘lgan jismning muvozanatda qolishi sharti |
Jismga ta’sir etayotgan kuch momentlarining vektor yig‘indisi nolga teng bo‘lganda jism muvozanatda qoladi: M→1 + M→2 + M→3 + ...... + M→n = 0. |
|
Ikki yelkali richag |
Tayanch richagning kuchlar qo‘yilgan nuqtalari oralig‘ida bo‘ladi. |
|
Bir yelkali richag |
Tayanch richagning bir uchiga joylashtirilgan bo‘lib, yuk richagning ikkinchi uchiga qo‘yiladi. |
|
Darajali polispast |
|
|
Laminar oqim |
Suyuqlikning qatlam-qatlam bo‘lib oqishi. |
|
Turbulent oqim |
Suyuqlikning uyurmali ko‘rinishdagi harakati. |
|
Oqim uzluksizligi tenglamasi |
Turli yuzali nayda oqayotgan siqilmas suyuqlik tezliklarining moduli, suyuqlik yuzalariga teskari proporsional bo‘ladi: S11 = S22. |
|
Bernulli tenglamasi |
|
|
Dinamik bosim |
Suyuqlikning harakati natijasida vujudga keladigan bosimi. |
|
Magnus effekti |
Aylanma harakat qilayotgan jism tomonlarida gaz yoki suyuqlik bosimlari farqi paydo bo‘lishi natijasida jismning harakat yo‘nalishini o‘zgarishi. |
|
Torrichelli formulasi |
= |
![]()
Turmushda uchraydigan harakatlarning ba’zilari teng vaqt oralig‘ida takrorlanib turadi. Bunday harakatlar davriy harakatlar deyiladi. Davriy harakatlar orasida jismning muvozanat vaziyati atrofi da goh bir tomonga, goh ikkinchi tomonga qiladigan harakati ko‘p uchraydi. Jismning bunday harakati tebranma harakat yoki qisqacha tebranishlar deyiladi.
Muvozanat vaziyatidan chiqarilgan jismning o‘z-o‘zidan ichki kuchlar ta’sirida qiladigan tebranishlari xususiy (erkin) tebranishlar deyiladi. Tebranayotgan jismning muvozanat vaziyatidan uzoqlashish masofasi uning siljishi (x) deyiladi. Muvozanat vaziyatdan eng katta chetlashishga tebranish amplitudasi (A) deyiladi.
Mexanik tebranishlarni kuzatish uchun prujina uchiga mahkamlangan yukning tebranishlari bilan tanishaylik (5.1-rasm). Bu rasmdagi prujinaga mahkamlangan yuk gorizontal sterjenda ishqalanishsiz harakatlana oladi, chunki sharchaning og‘irlik kuchini sterjenning reaksiya kuchi muvozanatlaydi.
Prujinaning elastiklik koeffi tsiyenti k, massasi hisobga olinmas darajada ki chik. Tizimning massasi yukda, bikrligi esa prujinada to‘plangan deb hisoblash mumkin.
![]() Agar muvozanat holatida turgan yukni o‘ng tomonga A
masofaga cho‘zib, qo‘yib yuborsak, yuk cho‘zilgan prujinada (5.1rasm) hosil
bo‘lgan elastiklik kuchi
Agar muvozanat holatida turgan yukni o‘ng tomonga A
masofaga cho‘zib, qo‘yib yuborsak, yuk cho‘zilgan prujinada (5.1rasm) hosil
bo‘lgan elastiklik kuchi
5. 1-rasm. Fel = –kA (5.1)
ta’sirida muvozanat vaziyati tomon harakat qila boshlaydi. Vaqt o‘tgan sari yukning siljishi A dan kamaya boradi, lekin yukning tezligi esa osha boradi. Yuk muvozanat vaziyatiga yetib kelgach, uning siljishi (x) nolga teng bo‘lganligi uchun elastiklik kuchi nolga teng bo‘lib qoladi. Lekin yuk inersiyasi tufayli chap tomonga qarab harakatlana boshlaydi. Prujinada hosil bo‘lgan elastiklik kuchining moduli ham orta boradi. Lekin elastiklik kuchi doim yukning siljishiga teskari yo‘nalganligi uchun, u yukni tormozlay boshlaydi. Natijada yukning harakati sekinlasha borib, nihoyat u to‘xtaydi. Endi yuk siqilgan prujinada hosil bo‘lgan elastiklik kuchi ta’sirida yana muvozanat holati tomon harakat qila boshlaydi.
Davriy ravishda tebranayotgan tizimning vaqt davomida qaysi qonun bo‘yicha o‘zgarayotganligini aniqlash uchun voronkaga qum to‘ldirib, uni ip bilan osib, tebrantirib yuboraylik. Voronkaning tebranish jarayonida uning tagidagi karton qog‘ozni bir tekis torta boshlasak, qumning qog‘ozidagi izning sinusoida shaklida ekanligiga guvoh bo‘lamiz. Bundan quyidagi xulosa kelib chiqadi: Davriy tebranayotgan jismning siljishi vaqt o‘tishi bilan sinuslar yoki kosinuslar qonuni bo‘yicha o‘zgaradi. Bunda siljishning eng katta qiymati amplituda A ga teng bo‘ladi:
x = Asin(ω0t + φ0), (5.2)
bu yerda: ω0 – tebranayotgan sistemaning parametrlariga bog‘liq bo‘lgan siklik chastotasi, φ0 – boshlang‘ich faza. (ω0t + φ0) esa tebranish boshlanganidan t vaqt o‘tgandagi tebranish fazasi.
![]() Matematikadan ma’lumki, shuning
uchun (5.2) ni
Matematikadan ma’lumki, shuning
uchun (5.2) ni
(5.3) deb ham yozish mumkin.
Vaqt davomida parametrlari sinus yoki kosinuslar qonuni bo‘yicha o‘zgaradigan tebranishlar garmonik tebranishlar deyiladi.
Demak, muvozanat vaziyatidan chiqarilgan prujinali mayatnik garmonik tebranar ekan. Sistema garmonik tebranishi uchun: 1) jism muvozanat vaziyatidan chiqarilganda unda tizimni muvozanat vaziyatiga qaytaruvchi ichki kuchlar hosil bo‘lishi; 2) tebranayotgan jism inertlikka ega bo‘lib, unga ishqalanish va qarshilik kuchlari ta’sir qilmasligi shart. Bu shartlar tebranma harakatning ro‘y berish shartlari deyiladi.
Garmonik tebranishlarning asosiy parametrlari:
a) tebranish davri T – bir marta to‘liq tebranish uchun ketgan vaqt:
![]() ; (5.4)
; (5.4)
b) tebranish chastotasi ν – 1 sekundda ro‘y beradigan tebranishlar soni:
![]() ; (5.5)
; (5.5)
Birligi [ν] = s–1 = Hz;
c) siklik chastota – 2 sekunddagi tebranishlar soni:
ω = 2. (5.6)
T
Garmonik tebranishlar tenglamasi (5.2) ni (5.5) va (5.6) larni hisobga olib quyidagi ko‘rinishlarda yozish mumkin.
x
= Asin(ω0t
+ φ0) =  = Asin(2πvt
+ φ0).
(5.7)
= Asin(2πvt
+ φ0).
(5.7)
Siljishi vaqt davomida sinus yoki kosinuslar qonuni bo‘yicha o‘zgaradigan garmonik tebranishlarni miqdor jihatidan tavsifl ovchi kattaliklarning aksa riyati (tezlik, tezlanish, kinetik va potensial energiyalari) ham garmonik o‘zgaradi. Buni quyidagi grafi k va tenglamalarda ko‘rishimiz mumkin:
![]() x
x
+xm
0x = Asin (ωt + φ0) (5.8)
– xm
+ωxm
0 = Aωcos (ωt + φ0) (5.9)
–ωxm
+ω2xma = –Aω2cos (ωt + φ0) =
0= Aω2cos [(ωt + φ0) + ] (5.10)
–ω2xm
5.2-rasm.
Masala yechish namunasi
1-masala. Nuqta garmonik tebranma harakat qilmoqda. Maksimal siljishi va tezligi mos ravishda 0,05 m va 0,12 m/s ga teng. Maksimal tezlanishini toping va siljish 0,03 m ga teng bo‘lgan momentda nuqtaning tezlik va tezlanishini toping.
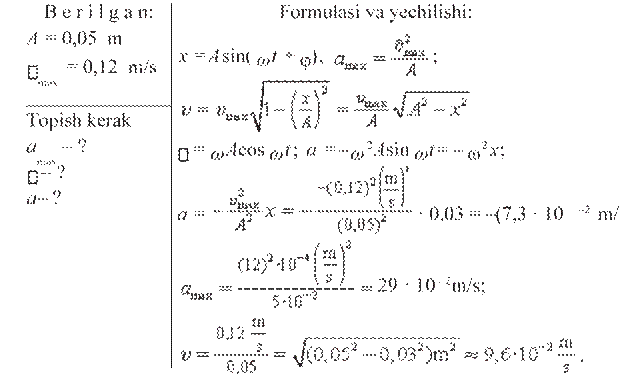
1.
![]() Davriy harakat deb qanday harakatga aytiladi? Davriy
harakatga turmushdan va texnikadan misollar keltiring.
Davriy harakat deb qanday harakatga aytiladi? Davriy
harakatga turmushdan va texnikadan misollar keltiring.
2. Garmonik tebranish harakat tenglamasini yozing.
3. Garmonik tebranishning siljishi, amplitudasi, davri, chastotasi deb nimaga aytiladi?
![]()
Davriy tebranma harakat qiladigan jism yoki jismlar sistemasi mayatnik deyiladi. Tabiatda uchraydigan aksariyat tebranma harakatlar: prujinali va matematik mayatnik larning harakatiga o‘xshash bo‘ladi.
Bikrligi k bo‘lgan prujinaga osilgan m massali yukdan iborat tizimga prujinali mayatnik deyiladi
(5. 3-rasm). Osilgan yuk ta’sirida prujina x0 masofaga x cho‘ziladi. Uning muvozanat sharti
ma = –kx0 (5.11)
![]() bilan aniqlanadi.
Prujinani biroz x ga cho‘zib, qo‘yib m yuborsak, yuk vertikal yo‘nalishda tebranma
harakatga
bilan aniqlanadi.
Prujinani biroz x ga cho‘zib, qo‘yib m yuborsak, yuk vertikal yo‘nalishda tebranma
harakatga
5.3-rasm. keladi.
Tajriba yordamida yuk siljishining vaqtga bog‘liqligi
x = Asin(ω0t + φ0)
qonun bo‘yicha o‘zgarishini aniqlagan edik. Garmonik tebranayotgan jismning tezlanishini (5.10) dan a = –ω02x ekanligini hisobga olsak, (5.10) tenglik quyidagi ko‘rinishga keladi:
![]() .
.
Bu tenglikdan
(5.12) ga ega bo‘lamiz.
Demak, garmonik tebranayotgan jismning siklik tebranish chastotasi tebranish sistemasiga kiruvchi jismlarning parametrlariga bog‘liq ekan. (5.12) prujinali mayatnikning siklik (davriy) chastotasini topish formulasi deyiladi.
![]() Tebranish davrining ta’rifi ga ko‘ra dan
Tebranish davrining ta’rifi ga ko‘ra dan
ya’ni
(5.13)
Prujinali mayatnikning tebranish davri osilgan yuk massasidan chiqarilgan kvadrat ildizga to‘g‘ri, prujina bikrligidan chiqarilgan kvadrat ildizga teskari proporsional bo‘ladi.
Prujinali mayatnikda energiya almashinishlarini qaraylik. Mayatnikning kinetik energiyasi prujinaning massasi hisobga olinmaganda,
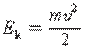 yukning kinetik energiyagasiga teng
bo‘ladi. Avvalgi mavzuda
yukning kinetik energiyagasiga teng
bo‘ladi. Avvalgi mavzuda
tezlik = Aω0cos(ω0t + φ0) ifoda bilan aniqlanishi ko‘rsatilgan edi. U holda mayatnikning kinetik energiyasi
![]() (5.14) ga teng bo‘ladi.
(5.14) ga teng bo‘ladi.
Prujinali mayatnikning potensial energiyasi prujinaning deformatsiya energiyasiga teng, ya’ni:
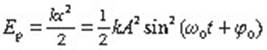 . (5.15)
. (5.15)
|
Ko‘pincha sistemaning to‘la energiyasi Et = Ek + Ep ni bilish katta |
|
|
ahamiyatga ega: Et = Ek + Ep = Agar
|
|
|
Et = |
(5.16) |
|
Et = |
(5.17) |
ekanligi kelib chiqadi.
E’tibor bering, prujinali mayatnikning to‘la energiyasi vaqtga bog‘liq bo‘lmagan doimiy kattalik ekan, ya’ni mexanik energiyaning saqlanish qonuni bajarilishi kuzatiladi.
Cho‘zilmas va vaznsiz ipga osilgan hamda muvozanat vaziyati atrofi da davriy tebranma harakat qiluvchi moddiy nuqta matematik mayatnik deyiladi.
Mayatnik turg‘un muvozanat vaziyatida bo‘lganda moddiy nuqtaning og‘irligi (P = mg) taranglik kuchi T ni muvoza natlaydi (5.4-rasm). Chunki ularning modullari teng bo‘lib, bir to‘g‘ri chiziq bo‘ylab, qarama-qarshi tomonga yo‘nalgan. Agar mayatnikni α burchakka og‘dirsak, mg va T kuchlar o‘zaro burchak tashkil qilib yo‘nalganligi uchun bir-birini muvozanatlay olmaydi. Bunday kuchlarning qo‘shilishidan mayatnikni muvozanat vaziyatiga qaytaruvchi kuch vujudga keladi.
![]() Mayatnikni qo‘yib yuborsak, mayatnik qaytaruvchi kuch
ostida muvozanat vaziyati tomon harakat qila boshlaydi. 5.4-rasmdan
Mayatnikni qo‘yib yuborsak, mayatnik qaytaruvchi kuch
ostida muvozanat vaziyati tomon harakat qila boshlaydi. 5.4-rasmdan
Fq = P sinα = mg · sinα (5.18) ekanligini ko‘ramiz.
Nyutonning ikkinchi qonuniga ko‘ra, Fq kuch moddiy nuqtaga a tezlanish beradi. Shuning uchun
–mg sinα = ma. (5.19) 5.4-rasm.
Juda kichik og‘ish burchaklarida (α ≤ 6° ÷ 8°) bo‘lganligi va Fq kuch doim siljishga qarama-qarshi yo‘nalganligi uchun (5.19) ni
ma ≈ –mg · x (5.20)
e
ko‘rinishda yozish mumkin. Agar moddiy nuqtaning (sharchaning) tebranish jarayonidagi siljishini x harfi bilan belgilasak hamda a = –ω02x munosabat e’tiborga olinsa, – mω02x = mg
(5.21)
![]() bo‘ladi. Tebranish davrining ta’rifi ga ko‘ra, bo‘lgani
uchun:
bo‘ladi. Tebranish davrining ta’rifi ga ko‘ra, bo‘lgani
uchun:
(5.22)
Matematik mayatnik tebranish davrini aniqlovchi bu formula Gyugens formulasi deb ataladi. Bundan matematik mayatnikning quyidagi qonunlari kelib chiqadi:
1) matematik mayatnikning og‘ish burchagi (α) kichik bo‘lganda tebranish davri uning tebranish amplitudasiga bog‘liq emas.
2) matematik mayatnikning tebranish davri unga osilgan yukning massasiga ham bog‘liq emas.
3) matematik mayatnikning tebranish davri uning uzunligidan chiqarilgan kvadrat ildizga to‘g‘ri proporsional va erkin tushish tezlanishidan chiqarilgan kvadrat ildizga teskari proporsional ekan.
Bunda matematik mayatnikning tebranishi x = Asin(ω0t + φ0) ifoda bilan belgilanadi.
Shuni ta’kidlash lozimki, tebranish amplitudasi yoki og‘ish
burchagi katta bo‘lganda, matematik mayatnikning tebranishi garmonik bo‘lmay
qoladi. Chunki, sinα ≈ ![]() ga teng bo‘lmaydi va
mayatnik harakat tenglamasining yechimi sinus yoki kosinus ko‘rinishida bo‘lmay
qoladi. Masala yechish namunasi
ga teng bo‘lmaydi va
mayatnik harakat tenglamasining yechimi sinus yoki kosinus ko‘rinishida bo‘lmay
qoladi. Masala yechish namunasi
1-masala. Birinchi mayatnikning tebranish davri 3 s ikkinchisiniki 4 s ga teng. Ular uzunliklari yig‘indisiga teng bo‘lgan mayatnikning tebranish davrini toping.
 s.
s.
1.
![]() Prujinali mayatnikning siklik chastotasini ikki marta
oshirish uchun uning qaysi parametrini necha marta o‘zgartirish kerak?
Prujinali mayatnikning siklik chastotasini ikki marta
oshirish uchun uning qaysi parametrini necha marta o‘zgartirish kerak?
2. Matematik mayatnik osilgan ipning og‘ish burchagi qaysi qonun bo‘yicha o‘zgaradi?
3. Qanday shart bajarilganda, matematik mayatnik tebranishlari garmonik bo‘ladi?
![]()
24-mavzu. LABORATORIYA ISHI: MATEMATIK MAYATNIK YORDAMIDA ERKIN TUSHISH TEZLANISHINI
Ishning maqsadi: Erkin tushish tezlanishini matematik mayatnik yordamida aniqlash usulini o‘rganish.
Kerakli asbob va jihozlar. Matematik mayatnik, laboratoriya universal shtativ, sekundomer, o‘lchov lentasi.
Ishni bajarish tartibi:
1. Ipni imkoni boricha uzunroq holatda mahkamlab, uning uzunligi o‘lchanadi. Shar radiusi r aniqlanadi. Olingan natija jadvalga yoziladi. l1 = (lip + r) m.
2. Sharchani muvozanat vaziyatidan uncha katta bo‘lmagan (6° – 8°) burchakka og‘dirib, u harakatga keltiriladi. Shu onda sekundomer ishga tushiriladi.
3. Matematik mayatnikning tebranishlar soni sanaladi. Mayatnik N1 = 20 marta tebranganda sekundomer to‘xtatiladi.
4. Sekundomerning ko‘rsatishi qayd etiladi va jadvalga yoziladi.
5.
T = ![]() dan tebranish davri aniqlanadi.
dan tebranish davri aniqlanadi.
6.
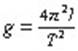 ifodaga ko‘ra erkin tushish tezlanishi
hisoblanadi.
ifodaga ko‘ra erkin tushish tezlanishi
hisoblanadi.
7. Mayatnik ipining uzunligini o‘zgartirmasdan tebranishlar soni N2 = 30 ta va N3 = 40 ta hollari uchin tajriba yuqoridagidek takrorlanadi.
8. Olingan natijalar asosida mayatnik tebranish davri va erkin tushish tezlanishining qiymatlari aniqlanib, jadvalga yoziladi.
9. Olingan natijalar asosida quyidagi jadval to‘ldiriladi.
|
li, m |
Ni |
ti, s |
ti, s |
gi, m/s2 |
|
∆g, m/s2 |
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
![]() 1. Nima
sababdan mayatnikning tebranish davri mayatnik sharcha massasiga bog‘liq
bo‘lmaydi?
1. Nima
sababdan mayatnikning tebranish davri mayatnik sharcha massasiga bog‘liq
bo‘lmaydi?
2. Nima sababdan Yerning turli geografi k kengliklarida mazkur tajriba o‘tkazilsa natija turlicha chiqadi?
3. Matematuk mayatnik sharchasining o‘lchamlari o‘zgartirilsa, uning tebranish davri qanday o‘zgaradi?
![]()
Biror muhitda sodir bo‘layotgan erkin tebranishlar so‘nuvchan bo‘ladi (5.5-rasm). Chunki tebranish davrida tebranuvchi jism muhit tomonidan ishqalanish tufayli qarshilikka uchraydi.
5.5-rasm.
Shu sababli erkin tebranishlardan amalda foydalanilmaydi.
Tebranishlar so‘nmasligi uchun ishlatilgan energiyani davriy tarzda to‘ldirib turish kerak. Buning uchun tebranuvchi sistemaga tashqi kuch vositasida davriy ta’sir ko‘rsatib turish kerak. Mana shunday tashqaridan kuch ta’sir etib turadigan qurilmaning sodda maketi 5.6-rasmda keltirilgan. Prujinaga osilgan yukni pastga tortib, qo‘yib yuborilsa, u tebranma harakat qiladi. Bu paytda prujina osilgan temir o‘zakning dastagi aylantirilsa, tebranishlar so‘nmaydi. Tashqaridan davriy ravishda ta’sir etib turadigan kuch ta’sirida sodir bo‘ladigan tizimning tebranishlariga majburiy tebranishlar deyiladi.
Bu majburiy tebranishlarni hosil qiluvchi davriy o‘zgaruvchi tashqi kuchga majburlovchi kuch deyiladi.
Majburiy tebranishlarga kundalik turmushdan ko‘plab misollar keltirish mumkin. Siz sevib tinglaydigan radiodagi, magnitofondagi, televizordagi radiokarnaylarning membranasi undan o‘tuvchi majburlovchi tok ta’sirida tebranadi. Uyingiz yoki sinfi ngiz yonidan og‘ir yuk ortgan mashinalar o‘tib qolsa deraza oynalari zirillaganini eshitasiz. Eski beton qurilmalar (fundament, ustun)ni parchalovchi, tog‘ jinslarini ko‘chiruvchi zirillab (titrab) ishlaydigan pnevmatik bolg‘alar ham davriy ravishda ta’sir etuvchi tashqi kuch ta’sirida ishlaydi. Majburiy tebranishlardan foydalanish yoki zararli hollarda yo‘qotish uchun ularni o‘rganish kerak. 5.6-rasmdagi qurilmadan foydalanib, tashqi majburlovchi kuchning tebranuvchi sistemada hosil bo‘ladigan tebranishlarga ta’sirini o‘rganamiz.
![]() Yuk (4) bog‘langan prujina (3) ning uchi
ilmoq (2) li sim uchiga osilgan. Ilmoq uchi halqa shaklida bolib, temir
o‘zak (l) ning yoy shaklida bukilgan qismida sirpanadi. Temir o‘zakni
aylantira boshlasak, yukli prujina tebrana boshlaydi.
Yuk (4) bog‘langan prujina (3) ning uchi
ilmoq (2) li sim uchiga osilgan. Ilmoq uchi halqa shaklida bolib, temir
o‘zak (l) ning yoy shaklida bukilgan qismida sirpanadi. Temir o‘zakni
aylantira boshlasak, yukli prujina tebrana boshlaydi.
O‘zak dastagini tezroq aylantirsak, yukning tebranishlari avvaliga biroz orqada qolib, keyin tenglashadi. Shunda tebranishlar barqaror bo‘ladi.
Bunda o‘zak vaqt birligi ichida necha marta aylansa, yukli prujina ham shuncha marta aylanadi. Demak, tebranuvchi siste- 5.6-rasm. mada sodir bo‘ladigan majburiy tebranishlar majburlovchi kuch chastotasiga teng bo‘lar ekan.
Majburiy tebranishlar so‘nmaydigan tebranishlardir.
Rezonans hodisasi
Endi tebranuvchi sistemada sodir bo‘layotgan tebranishlar amplitudasining majburlov chi kuchga qanday bog‘liq bo‘lishini kо‘rib chiqaylik. Buning uchun oddiyg ina tajriba o‘tkazamiz. 4–5 m uzunl ikdagi ipni xonaning bir uchidan ikkinchi uchiga biroz osiltirib tortamiz.
![]() Ularga 3–4
ta turli uzunlikdagi iplarga osilgan yuklarni bog‘laymiz (5.7-rasm).
Ularga 3–4
ta turli uzunlikdagi iplarga osilgan yuklarni bog‘laymiz (5.7-rasm).
Birinchi yuk osilgan ipning uzunligini to‘rtinchi yuk osilgan ip uzunligi bilan bir xil qilib tanlaymiz. Birinchi mayatnikni muvozanat vaziyatdan chetga chiqarib, qo‘yib yuborsak, u tebrana boshlaydi.
Uning tebranishi umumiy bog‘langan ip
5.7-rasm. orqali boshqa mayatniklarga o‘tib, ular ham asta-sekin tebranma harakatga keladi. Mayatniklarda barqaror tebranishlar vujudga kelgandan so‘ng ikkinchi, uchinchi va to‘rtinchi mayatniklar tebranishiga e’tibor bersak, to‘rtinchi mayatnik amplitudasi eng katta ekanligiga ishonch hosil qilamiz. To‘rtinchi va birinchi mayatniklar uzunligi bir xil bo‘lganligi tufayli, ularning erkin tebranishlar davri (chastotasi) o‘zaro teng bo‘lib chiqadi.
Demak, majburiy tebranishlarda majburlovchi kuch chastotasi, tebranuvchi sistemaning xususiy tebranishlari chastotasiga teng bo‘lganda tebranishlar amplitudasi eng katta bo‘ladi, ya’ni rezonans ro‘y beradi.
Tashqi majburlovchi kuch chastotasi, tebranuvchi sistemaning xususiy chastotasiga teng bo‘lganda, tebranishlar amplitudasining keskin ortib ketish hodisasiga rezonans deyiladi.
Rezonans davrida amplitudaning ortib ketishiga sabab majburlovchi kuch yo‘nalishi bilan tebranuvchi jism harakat yo‘nalishining o‘zaro mos keli- s hidir.
Rezonans hodisasidan texnikada va turmushda keng foydalaniladi. Soatlarda, barcha turdagi qo‘ng‘iroqlarda, sirenalarda, pnevmatik bolg‘alarda rezonans hodisasidan foydalaniladi.
Lekin rezonans hodisasi ba’zi hollarda zararlidir.
Masalan, daryo ustiga qurilgan osma ko‘prikdan odam o‘tayotgan paytda u tebranib turadi. Undan o‘tayotgan odamning sekin yoki tez yurishiga qarab ko‘prikning tebranishi kattalashishi yoki sekinlashishi mumkin. Agar qadam bosish chastotasi, ko‘prikning xususiy chastotasiga mos kelib qolsa, ko‘prikni tutib turuvchi tortqilar uzilib ketishi mumkin.
Rezonans zararli bo‘lgan hollarda uning oqibatini kamaytirish maqsadida tegishli choralar ko‘riladi. Korxonalarda dastgohlardagi qismlarning aylanishi natijasida rezonans bo‘lmasligi uchun bino poydevori og‘ir va katta qilib quriladi. Avtomobillardagi tebranishlarni tez so‘ndirish uchun amortizatorlar o‘rnatiladi.
Avtotebranishlar. So‘nmaydigan majburiy tebranishlarning bo‘lishi uchun tashqi davriy kuch ta’sir etib turishi kerak. Lekin sistemadagi tebranishlar tashqi davriy kuch ta’sirisiz ham so‘nmaydigan bo‘lishi mumkin. Agar erkin tebrana oladigan sistemaning ichida energiya manbayi bo‘lsa va bu manbadan tebranuvchi jismga yo‘qotgan energiyaning o‘rnini qoplash uchun zarur energiyaning kelib turishini sistemaning o‘zi rostlab tura olsa, bunday sistemada so‘nmaydigan tebranishlar yuzaga keladi.
Mayatnikli, oddiy soat bunday tipdagi sistemaning eng sodda misolidir. Bu sistema ma’lum energiya zahirasiga, ya’ni yerdan qandaydir balandlikka ko‘tarilgan yukning potensial energiyasiga yoki siqilgan prujina energiyasiga ega.
Energiya manbayidan ta’minlanishi tufayli so‘nmaydigan tebranishlar hosil qiladigan sistemalar avtotebranishli sistemalar deb ataladi. Elektr qo‘ng‘iroq, insonning yuragini va o‘pkasini ham avtotebranishli sistema deb qarash mumkin.
Sistemada tashqi davriy kuch ta’sirisiz ichki manba ta‘sirida bo‘la oladigan so‘nmas tebranishlar avtotebranishlar deb ataladi.
Majburiy tebranishlar chastotasi tashqi kuch chastotasi bilan bir xil bo‘ladi. Avtotebranishlarning chastotasi va amplitudasi sistemaning shaxsiy xususiyatlari bilan belgilanadi. Avtotebranishlar amplitudasi shu tebranishlarni yuzaga keltirgan dastlabki qisqa vaqtli ta’sir (turtki) kattaligiga bog‘liq emas.
![]() 1.
Erkin tebranishlarni so‘nmaydigan tebranishlarga aylantirish uchun nima qilish
kerak?
1.
Erkin tebranishlarni so‘nmaydigan tebranishlarga aylantirish uchun nima qilish
kerak?
2. Qanday tebranishlarga majburiy tebranishlar deyiladi?
3. Rezonans hodisasi qanday sharoitda vujudga keladi?
4. Rezonans foydali yoki zararli bo‘ladigan hollar uchun misol keltiring.
![]() Koptokni olib,
basketbolchilardek yerga urib o‘ynang. Koptokning harakati qanday harakatga
kiradi? Koptokning yerga to‘qnashish chastot asini va sapchish balandligini
o‘zgartiring. Qaysi holda koptokn ing harakati barqaror bo‘lishiga e’tibor
bering.
Koptokni olib,
basketbolchilardek yerga urib o‘ynang. Koptokning harakati qanday harakatga
kiradi? Koptokning yerga to‘qnashish chastot asini va sapchish balandligini
o‘zgartiring. Qaysi holda koptokn ing harakati barqaror bo‘lishiga e’tibor
bering.
![]()
26-mavzu. MEXANIK TO‘LQINLARNING MUHITLARDA TARQALISHI. ULTRA VA INFRATOVUSHLARDAN
Bizga ma’lumki, biror jismning muhitdagi tеbranma harakati shu jism turgan muhitga uzatiladi. Agar tеbranish havoda bo‘lsa, o‘zining harakatini havo zarrachalariga uzatadi. Havo zarrachalarining tеbranma harakati barcha yo‘nalishda havo bo‘ylab tarqaladi. Bu hodisa suyuqliklarda ham, qattiq jismlarda ham ro‘y bеradi. Vakuumda mexanik to‘lqinlar tarqalmaydi.
Tеbranishning muhitda vaqt bo‘yicha tarqalish jarayoniga to‘lqin dеyiladi.
Umuman olganda, mexanik to‘lqinlar ikki xil bo‘ladi: bo‘ylama va ko‘ndalang to‘lqinlar.
To‘lqin tarqalayotgan muhitda zarralarning tebranish yo‘nalishi, to‘lqin tarqalish yo‘nalishi bilan bir o‘qda bo‘lsa, bunday to‘lqinga bo‘ylama to‘lqin deyiladi.

5.8-rasm.
Bo‘ylama to‘lqinlar tarqalganda muhit siqilish va kengayish deformatsiyasiga uchraydi (5.8-rasm). Suyuqlik va gazlarda bunday deformatsiya muhit zarralarining zichlashishi yoki siyraklashishi orqali bo‘ladi. Bo‘ylama to‘lqinlar barcha muhitlar: qattiq, suyuq va gazsimon muhitlarda tarqalishi mumkin.
Bo‘ylama to‘lqinlarga misol tariqasida elastik sterjendagi to‘lqin yoki havoda tarqalgan tovushni keltirish mumkin.
To‘lqin tarqalayotgan muhitda zarralarning tebranish yo‘nalishi, to‘lqin tarqalish yo‘nalishiga perpendikulyar bo‘lsa, bunday to‘lqinga ko‘ndalang to‘lqin deyiladi.

5.9-rasm.
Ko‘ndalang to‘lqinlar tarqalganda muhitning bir qatlami, ikkinchisiga nisbatan siljiydi. Bunday to‘lqinlar tarqalganda muhitda do‘nglik va chuqurliklar hosil bo‘ladi (5.9-rasm). Qattiq jismlardan farqli ravishda, suyuqlik va gazlar qatlamlarning siljishiga nisbatan elastiklik xususiyatiga ega emas. Shunga ko‘ra ko‘ndalang to‘lqinlar faqat qattiq jismlarda tarqala oladi.
Ko‘ndalang to‘lqinning nuqtadan nuqtaga tebranishni uzatish jarayonini batafsil qaraylik. 5.10-rasmda ko‘ndalang to‘lqinning har ¼ T vaqtdagi holati keltirilgan.
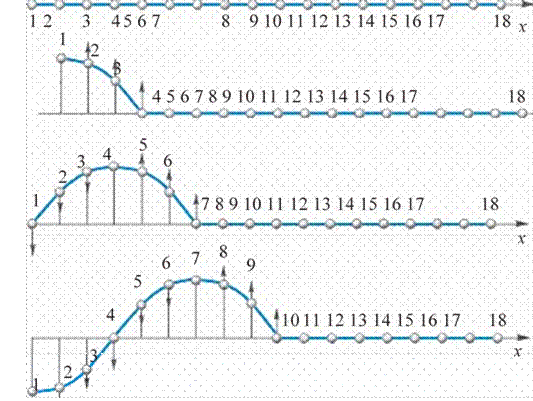
5.10-rasm.
5.10-rasmda zarralarning qandaydir momentdagi holati raqamlangan sharchalar ko‘rinishida berilgan. Sharchalar bir-biriga yaqin joylashganligidan ular orasida o‘zaro ta’sir mavjud. Agar birinchi sharchani tebranma harakatga keltirsak, ya’ni uni yuqoriga va pastga harakatlanishga majbur qilsak, sharchalar orasidagi o‘zaro ta’sir tufayli qolganlari ham uning harakatini takrorlaydi. Lekin ularning harakati oldingisiga nisbatan kechikkan (faza jihatidan siljigan) holda bo‘ladi.
Masalan, to‘rtinchi shar, birinchi shardan ¼ tebranishga orqada bo‘ladi. Yettinchi shar harakati, birinchi shardan ½ ta tebranishga, o‘ninchisi ¾ ta tebranishga orqada qoladi. O‘n uchinchi shar birinchi shardan bitta to‘liq tebranishga orqada qoladi, ya’ni u bilan bir xil fazada tebranadi.
![]() Ikkita bir-biriga
eng yaqin oraliqda joylashgan va bir xil fazada tebranayotgan nuqtalar
orasidagi masofaga to‘lqin uzunligi deyiladi.
Ikkita bir-biriga
eng yaqin oraliqda joylashgan va bir xil fazada tebranayotgan nuqtalar
orasidagi masofaga to‘lqin uzunligi deyiladi.
To‘lqin uzunligi grekcha λ (“lambda”) harfi bilan belgilanadi. Birinchi va o‘n uchinchi shar, ikkinchi va o‘n to‘rtinchi, uchinchi va o‘n beshinchi sharlar orasidagi masofa bitta to‘lqin uzunligiga teng deyiladi.
Demak, bir davr ichida to‘lqin tarqalgan masofa to‘lqin uzunligiga teng bo‘ladi:
![]() x, m λ
= T.
x, m λ
= T.
Bunda
– to‘lqin tarqalish tezligi (5.11rasm). Tebranish davrining chastotaga
bog‘liqligi ![]() e‘tiborga olinsa, bo‘ladi.
Birligi [ λ ] = 1 m.
e‘tiborga olinsa, bo‘ladi.
Birligi [ λ ] = 1 m.
Hovuzga yoki tinch shamolsiz vaqtda suv yuzasiga tosh tashlansa, tosh tushgan nuqtadan boshlab hamma tomonga tеbranishlar tarqala boshlaydi. Bu to‘lqinlar aylana shaklida bo‘lib, do‘ngliklar va chuqurliklardan iborat bo‘ladi.
Tor tеbranishlarining, shu tor bo‘ylab tarqalishi oddiy to‘lqinga misol bo‘la oladi.
Undagi tеbranishning tarqalish tеzligi  va
shuning uchun:
va
shuning uchun:
a)
tarqalish tеzligi torning taranglik kuchi T va uning
chiziqli zichligi ![]() ga bog‘liq;
ga bog‘liq;
b) muhitning elastikligi qancha katta bo‘lsa, tеbranishlarning tarqalish
tеzligi shuncha katta bo‘ladi.
Tovush va uning tabiati. Elastik muhitda tarqalayotgan to‘lqinlarning chastotasi 20 Hz dan (ba’zi adabiyotlarda 16 yoki 17 Hz) 20000 Hz gacha bo‘lsa, bunday mеxanik to‘lqinlarni inson eshitish organi sеzadi. Bunday to‘lqinlar – tovush to‘lqinlari yoki tovush dеb ataladi. Chastotasi 20 Hz dan kichik bo‘lgan to‘lqinlar infratovush dеb ataladi va buni inson sеzmaydi.
Chastotasi 1 Hz dan 1013 Hz gacha bo‘lgan to‘lqinlarni xususiyatini o‘rganadigan fi zikaning bo‘limiga akustika dеyiladi.
Tovush bo‘ylama to‘lqin bo‘lib, muhitning zichligiga, uning xususiyatiga bog‘liq bo‘lgan tеzlik bilan tarqaladi.
Shuni ta’kidlash kеrakki, muhitning harorati doimiy bo‘lganda
bosimning o‘zgarishi zichlikning o‘zgarishiga to‘g‘ri proporsional va  bo‘lgani
uchun gazlarda tovushning tarqalish tеzligi bosimga bog‘liq bo‘lmay qoladi.
bo‘lgani
uchun gazlarda tovushning tarqalish tеzligi bosimga bog‘liq bo‘lmay qoladi.
Lеkin gazlarda tovushning tarqalish tеzligi uning temperaturasiga bog‘liq.
![]() Qattiq jismlarda esa,
ham bo‘ylama, ham ko‘ndalang to‘lqinlar tarqaladi, shuning uchun tovushning
bo‘ylama tеzligi
Qattiq jismlarda esa,
ham bo‘ylama, ham ko‘ndalang to‘lqinlar tarqaladi, shuning uchun tovushning
bo‘ylama tеzligi  , ko‘ndalang to‘lqin tarqalish tеzligi
, ko‘ndalang to‘lqin tarqalish tеzligi 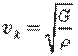 formula
bilan hisoblanadi.
formula
bilan hisoblanadi.
Bu yerda: Е – muhit uchun Yung moduli, G – siljish moduli. Qattiq jismlarda bo‘ylama to‘lqinlarning tarqalish tеzligi ko‘ndalang to‘lqinlarning tarqalish tеzligidan dеyarli ikki marta katta, chunki E > G.
Shuning uchun yer qimirlashini ikki marta sеzamiz, chunki yer qimirlash markazidan biz turgan joyga bo‘ylama to‘lqin avvalroq, ko‘ndalang to‘lqin esa kеyinroq yetib kеladi.
Inson qulog‘ining tovushni sеzish va eshitish sohasi chastotasi 16 Hz dan 20000 Hz bo‘lgan tovushlarga to‘g‘ri kеladi.
Chastotasi 20 kHz dan yuqori bo‘l gan tovush to‘lqinlari ultratov ushl ar deyiladi. Ultratovushlar o‘ziga xos xossalarga ega bo‘lib, xususan, ular yorug‘lik nurlari kabi fazoda ingichka nur ko‘rinishida tarqaladi.
Ultratovushlar quyidagi sohalarda keng qo‘llaniladi:
1) ultratovushlar metallar ichidagi yoriqlarni, suv ostidagi buyumlarni, shu jumladan, dengiz baliqlarining galasi joylashgan joylarni aniqlashda;
2) qattiq, suyuq va gaz holatida jismlarning fi zik xossalarini o‘rganishda.
3) o‘ta qattiq va mo‘rt jismlarga mexanik ishlov berishda, ularni tozal ashda;
4) tibbiyotda buyrak, jigar, homila va shu kabi inson ichki a’zolarining holatini o‘rganishda foydalaniladi.
Ko‘rshapalaklar o‘zi chiqarayotgan ultratovushning ro‘parasidagi to‘siqdan qaytgan qismini qabul qilib, to‘siqni sezadi va borib urilmaydi.
1.
![]() Bo‘ylama va ko‘ndalang to‘lqinlar bir-biridan nimasi
bilan farql anadi?
Bo‘ylama va ko‘ndalang to‘lqinlar bir-biridan nimasi
bilan farql anadi?
2. Bo‘ylama to‘lqinlar tarqalganda muhit qanday deformatsiyaga uchraydi?
3. To‘lqin uzunligini qanday aniqlash mumkin?
5-mashq
1.
Matematik mayatnik 1 min 40 s ichida 50 marta tebrandi.
Mayatnikning tebranish davri va siklik chastotasini toping. (Javobi: 2
s, π ![]() ).
).
2. Tebranma harakat tenglamasi x = 0,06cos100πt ko‘rinishda berilgan. Tebranma harakat amplitudasi, chastotasi va davrini toping. (Javobi: 6 sm, 50 Hz, 20 ms).
3. Nuqta garmonik tebranma harakat qiladi. Eng katta siljish A = 10 sm, tezlikning eng katta qiymati m = 20 sm/s. Tebranishlarning siklik chastotasi va nuqtaning maksimal tezlanishi topilsin. (Javobi: 2 rad/s; 0,4 m/s2).
4. Nuqta amplitudasi A = 0,1 m, davri T = 2 s bo‘lgan garmonik tebranma harakat qilmoqda. Siljish x = 0,06 m bo‘lgan momentdagi tezlik va tezlanish topilsin. (Javobi: 0,25 m/s; 0,6 m/s2)
5. Davrning qanday
bo‘lagida nuqtaning tezligi uning maksimal qiymatining yarmiga teng bo‘ladi?
Garmonik tebranishlarning boshlang‘ich fazasi nolga teng. (Javobi: ![]() T).
T).
6. Moddiy nuqta amplitudasi A = 5 sm bo‘lgan garmonik tebranma harakat qiladi. Agar nuqtaga F = 0,2 N elastik kuch ta’sir etsa, nuqtaning kinetik, potensial va to‘la energiyasi topilsin.
7. Bikrligi 100 N/m, yukining massasi 10 g bo‘lgan prujinali mayatnik ning tebranishlar chastotasi qanday (Hz)? (Javobi: 16 Hz).
8. Agar prujinali mayatnik prujinasining yarmi kesib tashlansa, uning tebranishlari chastotasi qanday o‘zgaradi?
9. Matematik mayatnikning uzunligi 2,5 m, unga osilgan sharchaning massasi 100 g. Tebranish davri qanday (s)? (Javobi: 3,14 s).
10. Tubida kichik teshigi bor suvli chelak arqonga osilgan holda tebranmoqda. Suvning kamayishi bilan tebranish davri qanday o‘zgaradi?
11. Bir xil vaqt oralig‘ida birinchi mayatnik 50 marta, ikkinchi mayatnik 30 marta tebrandi. Agar ularning biri ikkinchisidan 32 sm qisqa bo‘lsa, mayatniklarning uzunligini toping.
12. Massasi 20 kg bo‘lgan o‘quvchi arg‘imchoq uchmoqda. Arg‘imchoq muvozanat vaziyatidan maksimum 1 m ga og‘ayotgan va munutiga 15 marta tebranayotgan bo‘lsa, tebranish davrining 1/12 qismidagi kinetik va potinsial energiyasini toping
1. Tebranishlar amplitudasi 2 marta orttirilsa, uning davri qanday o‘zgaradi?
A) 2 marta ortadi; B) 2 marta kamayadi;
C) 4 marta ortadi; D) o‘zgarmaydi.
2. Matematik mayatnik uzunligi 16 marta kamaysa, uning erkin (xususiy) tebranishlar davri qanday o‘zgaradi?
A) 16 marta kamayadi; B) 16 marta ortadi; C) 4 marta ortadi; D) 4 marta kamayadi.
3.
![]() Sharchalar o‘zaro qanday fazada tebranmoqda?A) 1 va
3 qarama-qarshi, 2 va 3 fazasi bir xil;
Sharchalar o‘zaro qanday fazada tebranmoqda?A) 1 va
3 qarama-qarshi, 2 va 3 fazasi bir xil;
B) 1 va 2 qarama-qarshi, 2 va 3 bir xil;
C) 1 va 2 bir xil, 2 va 3 qarama-qarshi;
D) 1 va 2 qarma-qarshi, 1 va 3 bir xil. 1 2 3
4. Bo‘ylama to‘lqinlar qanday muhitlarda tarqaladi? 1 – qattiq jismlarda; 2 – suyuqliklarda; 3 – gazsimon moddalarda.
A) faqat 1; B) faqat 2; C) faqat 3; D) 1, 2 va 3 da.
5. Gapni to‘ldiring. “Tebranishlar tarqalayotgan muhitda birday fazada tebranayotgan ikki nuqta orasidagi eng... deyiladi”.
A) ... yaqin masofa to‘lqin uzunligi;B) ... katta siljish amplituda;
C) ... uzoq masofa to‘lqin uzunligi;
D) ... katta tebranishlar soni chastota.
6. Gapni to‘ldiring. “Ko‘ndalang to‘lqinlar ... to‘lqinlaridir”.
A) ... siqilish; B) ... kengayish;
C) ... siqilish-kengayish; D) ... siljish.
7. Muhitda tarqalayotgan to‘lqinning davri 10 s, to‘lqin uzunligi 5 m bo‘lsa, to‘lqinning tarqalish tezligi nimaga teng bo‘ladi?
A) 0,5 m/s; B) 2 m/s; C) 50 m/s; D) 5 m/s.
8. Agar moddiy nuqta tebranishlari amplitudasi 4 sm bo‘lsa, uning bir to‘la tebranish davomida bosib o‘tgan yo‘li qanday (sm) bo‘ladi?
A) 0; B) 4; C) 8; D) 16.
9. Siklik chastota deb nimaga aytiladi?
A) 1 sekunddagi tebranishlar soniga;
B) bitta tebranish uchun ketgan vaqtga;
C) 2 sekunddagi tebranishlar soniga;
D) burchak tezlikning 1 sekunddagi o‘zgarishiga.
10. Bikrligi 160 N/m bo‘lgan prujinaga 400 g yuk osildi. Hosil bo‘lgan mayatnikning tebranish chastotasi qanday (Hz)?
A) 1,6; B) 3,2; C) 5,4; D) 20.
|
Tebranma harakat |
Har qanday takrorlanuvchi harakat. |
|
Tebranishlar davri |
Bir marta to‘la tebranish uchun ketgan vaqt. [T] = 1 s. |
|
Erkin tebranishlar |
Faqat boshlang‘ich berilgan energiya hisobiga sodir bo‘ladigan tebranishlar. |
|
Tebranayotgan jismning siljishi |
Tebranayotgan jismning istalgan lahzada muvozanat vaziyatiga nisbatan joylashgan o‘rnini ko‘rsatuvchi kattalik. |
|
Tebranishlar chastotasi |
Vaqt birligi ichidagi tebranishlar soni. v = 1/T; [v] = 1/s = l Hz. |
|
Prujinali mayatnik |
Bikrligi k bo‘lgan prujinaga m massali yuk osilib,
erkin tebrana oladigan sistema: |
|
Matematik mayatnik |
Cho‘zilmas, vaznsiz ipga osilgan, o‘lchamlari ip uzunligiga nisbatan hisobga olmas darajada kichik bo‘lgan sharchadan iborat tebranuvchi sistema. T
= 2π |
|
So‘nuvchi tebranishlar |
Vaqt o‘tishi bilan amplitudasi kamayib boruvchi tebranishlar. Erkin tebranishlar – so‘nuvchi tebranish lardir. |
|
Rezonans hodisasi |
Tashqi majburlovchi kuch chastotasi tebranuvchi sistemaning erkin (xususiy) tebranishlari chastotasiga teng bo‘lganda tebranishlar amplitudasining keskin ortib ketishi. |
|
Bo‘ylama to‘lqinlar |
To‘lqin tarqalayotgan muhit zarralarining tebranish yo‘nalishi bilan to‘lqin tarqalish yo‘nalishi o‘zaro mos tushadigan to‘lqinlar. Qattiq, suyuq va gazsimon muhitlarda tarqaladi. |
|
Ko‘ndalang to‘lqinlar |
To‘lqin tarqalayotgan muhit zarrachalarining tebranish yo‘nalishi bilan to‘lqin tarqalish yo‘nalishi o‘zaro perpendikulyar bo‘lgan to‘lqinlar. Ular faqat qattiq jismlarda tarqaladi. |
|
To‘lqin uzunligi |
To‘lqinning bir davr ichida bosib o‘tgan masofasi: λ = T. Birligi [λ] = 1 m. |

![]()
Termodinamik jarayonda sistema boshlang‘ich holatdan oraliq holatlar orqali oxirgi holatga o‘tadi. Bu o‘tish qaytar va qaytmas bo‘lishi mumkin.
Qaytar jarayon deb, sistema biror holatga o‘tganda oxirgi holatdan boshlang‘ich holatga o‘sha oraliq holatlar orqali teskari ketma-ketlikda o‘tishiga aytiladi.
Masalan, ishqalanishsiz bo‘ladigan barcha sof mexanik jarayonlar qaytar jarayonga misol bo‘ladi. Jumladan, uzun ilgakka osilgan og‘ir mayatnikning tebranishi qaytar jarayonga yaqin bo‘ladi. Bu holda kinetik energiya amalda to‘la potensial energiyaga aylanadi. Shuningdek, teskarisi ham o‘rinli. Muhitning qarshiligi kichik bo‘lganligi sababli tebranish amplitudasi sekin kamayadi va tebranish jarayoni uzoq davom etadi.
Ma’lum qarshilikka uchraydigan yoki issiq jismdan sovuq jismga issiqlik uzatish bilan ro‘y beradigan har qanday jarayon qaytmas bo‘ladi. Amalda barcha real jarayonlar qaytmas jarayonlardir. Yuqoridagi keltirilgan mayatnik misolidagi jarayon ham qaytmasdir, chunki ishqalanishni yo‘qotib bo‘lmaydi. Shu sababli mexanik energiyaning bir qismi hamma vaqt issiqlikka aylanadi va qaytmas bo‘lib atrof-muhitga sochilib ketadi, demak, atrofdagi jismlarda o‘zgarish sodir bo‘ladi, shuning uchun jarayon qaytmas deyiladi.
Shuningdek, issiq jismdan sovuq jismga issiqlik miqdorining uzatilish jarayoni ham qaytmas jarayonlarga misol bo‘la oladi.
Umuman, tabiatda qaytar jarayonlar mavjud emas. Real jarayonlarning hammasi qaytmasdir. Qaytar jarayonlar ideallashtirilgan tushunchadir.
Ichki energiya. Termodinamik sistema ko‘plab molekulalar va atomlardan tashkil topganligi sizga ma’lum. U ichki energiyaga ega, ya’ni molekulalar doimo harakatda bo‘lganligi uchun kinetik energiyaga ega. Shu bilan birga modda molekulalari orasida o‘zaro ta’sir kuchi bo‘lganligi sababli molekulalar o‘zaro ta’sir potensial energiyasiga ega bo‘ladi.
Termodinamik sistemaning ichki energiyasi deb, uning barcha molekul alarining tartibsiz harakat kinetik energiyal ari va ularning o‘zaro ta’sir potensial energiya larining yig‘indisiga aytiladi.
Jismning ichki energiyasini mexanik energiya bilan almashtirmaslik kerak, chunki mexanik energiya jismning boshqa jismlarga nisbatan harakatiga va joylashuviga bog‘liq bo‘lsa, shu jismning ichki energiyasi jismni tashkil etuvchi zarralarning harakatiga va bir-biriga nisbatan joylashuviga bog‘liqdir.
![]() Ichki energiya termodinamik sistemaning bir qiymatli
funksiyasidir, ya’ni sistemaning har bir holatiga ichki energiyaning aniq bir
qiymati to‘g‘ri kelib, u sistema bu holatga qanday qilib kelib qolganiga
mutlaqo bog‘liq emas. Agar gaz qizitilsa, molekula va atomlarning tezliklari
ham ortadi. Bu esa ichki energiyaning ortishiga olib keladi. Agar bosim yoki
solishtirma hajm o‘zgartirilsa, bu ham ichki energiyaning o‘zgarishiga olib
keladi, chunki molekulalar orasidagi masofa o‘zgaradi. Demak, ularning o‘zaro
ta’sir potensial energiyalari ham o‘zgaradi.
Ichki energiya termodinamik sistemaning bir qiymatli
funksiyasidir, ya’ni sistemaning har bir holatiga ichki energiyaning aniq bir
qiymati to‘g‘ri kelib, u sistema bu holatga qanday qilib kelib qolganiga
mutlaqo bog‘liq emas. Agar gaz qizitilsa, molekula va atomlarning tezliklari
ham ortadi. Bu esa ichki energiyaning ortishiga olib keladi. Agar bosim yoki
solishtirma hajm o‘zgartirilsa, bu ham ichki energiyaning o‘zgarishiga olib
keladi, chunki molekulalar orasidagi masofa o‘zgaradi. Demak, ularning o‘zaro
ta’sir potensial energiyalari ham o‘zgaradi.
Odatda, sistemaning ichki energiyasi T = 0 K da nolga teng deb hisoblanadi, lekin bu muhim ahamiyatga ega emas. Chunki sistema bir holatdan ikkinchisiga o‘tganda ichki energiyaning o‘zgarishi ΔU ahamiyatga ega bo‘ladi.
Termodinamikaning birinchi qonuni. Buning uchun qizdirilayotgan choynak misolini ko‘raylik. Choynak olayotgan issiqlik miqdori Q ichidagi suvning qizishiga, ya’ni suvning ichki energiyasi ortishiga ΔU va suv bug‘lari choynak qopqog‘ini ko‘targanda tashqi kuchlarga qarshi (qopqoqning og‘irlik kuchi) bajariladigan A ishga sarfl anadi. Bu jarayon uchun energiyaning saqlanish va aylanish qonuni
Q = ΔU + A (6.1)
ko‘rinishga ega bo‘ladi. Bu termodinamikaning birinchi qonunining matematik ko‘rinishidir.
Termodinamik sistemaga beriladigan issiqlik miqdori uning ichki energiyasini orttirishi va tashqi kuchlarga qarshi bajargan ishning yig‘indisiga teng.
Agar sistemaga issiqlik miqdori berilayotgan bo‘lsa, Q musbat, agar sistemadan issiqlik miqdori olinayotgan bo‘lsa, Q manfi y ishora bilan olinadi. Shuningdek, agar sistema tashqi kuchlarga qarshi ish bajarayotgan bo‘lsa, A ish musbat, tashqi kuchlar sistema ustida ish bajarayotgan bo‘lsa, A ish manfi y bo‘ladi.
Termodinamikaning birinchi qonuni birinchi tur abadiy dvigatel (lotincha “perpetuum mobile”) yasash mumkin emasligini ko‘rsatadi. Birinchi tur “perpetuum mobile”ga asosan teng miqdorda energiya sarfl amasdan ish bajara oladigan mashina qurish haqida fi kr yuritiladi. Energiyaning saqlanish va aylanish qonuni bo‘lgan termodinamikaning birinchi qonunida esa tabiatda ro‘y beradigan barcha jarayonlarda energiya o‘z-o‘zidan paydo bo‘lmaydi va yo‘qolmaydi, faqat bir ko‘rinishdan boshqasiga aylanishi mumkin, deb qayd etiladi. Termodinamikaning birinchi qonuni quyidagicha ham ta’rifl anadi:
Sistema bir holatdan ikkinchi holatga o‘tganda ichki energiyaning o‘zgarishi tashqi kuchlarning ishi (A') va sistemaga berilgan issiqlik miqdori (Q) ning yig‘indisiga teng:
ΔU = Q + A'. (6.2)
Termodinamikaning birinchi qonuni energiyaning saqlanish va aylanish qonunini ifodalasa-da, termodinamik jarayonning ro‘y berish yo‘nalishini ko‘rsata olmaydi. Misol uchun birinchi qonun, issiqlik miqdorining issiq jismdan sovuq jismga o‘tish imkoniyati qanday bo‘lsa, sovuq jismdan issiq jismga o‘tish imkoniyati ham shunday deb ko‘rsatadi. Aslida esa “Tabiatda o‘z-o‘zidan qanday jarayonlar ro‘y berishi mumkinˮ, degan savol tug‘iladi. Bunga termodinamikaning ikkinchi qonuni javob beradi.
![]() Termodinamikaning
ikkinchi qonuni. Bu qonun ta’rifi ning bir nechta shakllari mavjud bo‘lib,
ularning eng soddasi Klauzius ta’rifi ni keltiramiz. Issiqlik o‘z-o‘zidan
past temperaturali jismdan yuqori temperaturali jismga o‘tmaydi.
Termodinamikaning
ikkinchi qonuni. Bu qonun ta’rifi ning bir nechta shakllari mavjud bo‘lib,
ularning eng soddasi Klauzius ta’rifi ni keltiramiz. Issiqlik o‘z-o‘zidan
past temperaturali jismdan yuqori temperaturali jismga o‘tmaydi.
Amalda cheksiz katta bo‘lgan okean suvlaridagi issiqlik o‘z-o‘zidan temperaturasi suvnikidan pastroq bo‘lgan jismgagina o‘tishi mumkin. Issiqlikni temperaturasi past jismdan temperaturasi yuqori jismga o‘tkazish uchun qo‘shimcha ish bajarish kerak. Shu bilan birga, issiqlik miqdori ishga to‘la aylanmay, uning bir qismi atrof-muhitni qizdirishga sarfl anadi. Shu nuqtayi nazardan ikkinchi qonunning Plankning quyidagi ta’rifi ham e’tiborga molik: tabiatda issiqlik miqdori to‘laligicha ishga aylanadigan jarayon bo‘lishi mumkin emas.
Issiqlik ishga aylanishi uchun isitkich va sovitkich bo‘lishi kerak. Barcha issiqlik mashinalarida isitkichdan sovitkichga beriladigan energiyaning bir qismigina foydali ishga aylanadi. Unda issiqlik mashinalarining FIK qanday kattaliklarga bog‘liq va uni oshirish uchun nima qilmoq kerak degan savol tug‘iladi. Bu savolga termodinamikaning ikkinchi qonunning Karno ta’rifi
javob beradi: ideal issiqlik mashinasining foydali ish koeffi tsiyenti issiqlik beruvchi va issiqlik oluvchilarning temperaturalari farqi bilangina aniqlanadi.
Termodinamika qonunlari amalda qanday issiqlik mashinalari yasash mumkinligi va ularning FIKni orttirish uchun nimalarga e’tibor berish zarurligi haqida yo‘llanma beradi.
Ikkinchi tur “perpetuum mobile”. Ikkinchi tur “perpetuum mobile”okean suvlaridagi ulkan miqdordagi energiyadan ish bajarmasdan foydalanish mumkin degan g‘oyaga asoslangan. Termodinamikaning ikkinchi qonuni esa issiqlik miqdori faqat issiq jismdan sovuq jismga o‘z-o‘zidan o‘tishi mumkin, teskarisi uchun esa qo‘shimcha ish bajarish zarur deb ta’kidlaydi. Bu esa ikkinchi tur “perpetuum mobile”ni yasash mumkin emasligini ko‘rsatadi.
Agar ikkinchi tur “perpetuum mobile”ni yasash mumkin bo‘lganda edi insoniyat juda ulkan energiya manbayiga ega bo‘lardi. Okeanlarda mavjud 1021 kg suvning temperaturasini 1 °C ga pasaytirishga erishilsa, bu 1024 J issiqlik miqdori ajratib olishga imkon beradi. Shuncha energiya beruvchi ko‘mirni temir yo‘l sostaviga yuklasak, uning uzunligi 1010 km ni tashkil etadi. Bu esa qariyib Quyosh sistemasining diametriga teng masofadir.
1.
![]() Termodinamikaning birinchi qonuni jarayonning ro‘y
berish yo‘nal ishin i ko‘rsata oladimi?
Termodinamikaning birinchi qonuni jarayonning ro‘y
berish yo‘nal ishin i ko‘rsata oladimi?
2. Termodinamikaning ikkinchi qonuni ta‘rifl arini ayting.
3. Termodinamika ikkinchi qonunining ahamiyati nimada?
4. Tabiatda issiqlik miqdori to‘laligicha ishga aylanadigan jarayon bo‘lishi mumkinmi?
5. Issiqlik mashinasining foydali ish koeffi tsiyenti nimalarga bog‘liq?
![]()
![]() Adiabatik
jarayon.
Adiabatik
jarayon.
Atrof-muhit bilan issiqlik miqdori almashmasdan ro‘y beradigan jarayonga adiabatik jarayon deyiladi.
Adiabatik jarayonga tez ro‘y beradigan jarayon misol bo‘ladi. Misol uchun gaz tez siqilganda bajarilgan ish uning temperaturasining, ya’ni ichki energiyasining ortishiga olib keladi. Temperatura ortishi natijasida atrofga issiqlik miqdori tarqalishi uchun esa ma’lum vaqt kerak. Shuning uchun ham Q = 0. Ichki yonish dvigatelida yonilg‘i aralashmasining yonishi adiabatik jarayonga misol bo‘ladi.
Adiabatik jarayon uchun termodinamikaning birinchi qonuni quyidagi ko‘rinishda bo‘ladi:
ΔU + A = 0 yoki A = –ΔU, (6.3) ya’ni adiabatik jarayonda ish ichki energiyaning o‘zgarishi hisobiga bajariladi.
Issiqlik mashinasi deb, yoqilg‘ining ichki ener giyasini mexanik energiyaga aylantirib beradigan mashinalarga aytiladi.
![]() Issiqlik
mashinasining ish prinsipi 6.1-rasmda ko‘rsatilgan. Bir siklda T1 temperaturali
isitkichdan Q1
issiqlik miqdori olinib, T2 temperaturali sovitkichga Q2 issiqlik miqdori
qaytariladi va A = Q1 – Q2 miqdordagi ish bajariladi. 6.2-rasmda issiqlik
mashinasining tuzilishi ko‘rsatilgan. Har qanday dvigatel uchta qismdan iborat:
ishchi modda (gaz yoki bug‘), isitkich va sovitkich. Isitkichdan Q1 issiqlik miqdori olgan
ishchi modda kengayib ish bajaradi. Yoqilg‘ining yonishi natijasida
isitkichning temperaturasi T1 o‘zgarmas bo‘lib qoladi.
Issiqlik
mashinasining ish prinsipi 6.1-rasmda ko‘rsatilgan. Bir siklda T1 temperaturali
isitkichdan Q1
issiqlik miqdori olinib, T2 temperaturali sovitkichga Q2 issiqlik miqdori
qaytariladi va A = Q1 – Q2 miqdordagi ish bajariladi. 6.2-rasmda issiqlik
mashinasining tuzilishi ko‘rsatilgan. Har qanday dvigatel uchta qismdan iborat:
ishchi modda (gaz yoki bug‘), isitkich va sovitkich. Isitkichdan Q1 issiqlik miqdori olgan
ishchi modda kengayib ish bajaradi. Yoqilg‘ining yonishi natijasida
isitkichning temperaturasi T1 o‘zgarmas bo‘lib qoladi.
Siqilishda ishchi modda Q1 issiqlik miqdorini T2 temperaturali sovitkichga uzatadi. Issiqlik dvigateli siklik ravishda ishlashi kerak.
Aylanma jarayon yoki sikl deb sistema bir qancha holatlardan o‘tib, dastlabki holatiga qaytadigan jarayonga aytiladi (6.3-rasm). Soat strelkasi aylanishi bo‘ylab ro‘y beradigan jarayon (gaz oldin kengayib, keyin siqiladi) to‘g‘ri sikl, soat strelkasi aylanishiga teskari yo‘nalishda (gaz oldin siqilib, keyin kengayadi) ro‘y beradigan jarayon esa teskari sikl deyiladi. Issiqlik mashinalari to‘g‘ri sikl, sovitkichlar esa teskari sikl asosida ishlaydi. Sikl tugaganda ishchi modda o‘zining dastlabki holatiga qaytadi, ya’ni uning ichki energiyasi boshlang‘ich qiymatiga ega bo‘ladi.
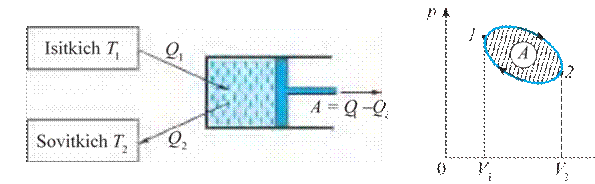
6.2-rasm. 6.3-rasm.
|
0 V1 V4 V2 V3 V 6.4-rasm. |
o‘rnat ilgan porshenli silindr misolida ko‘rib chiqamiz. |
![]() pKarno sikli
– navbatma-navbat oʻzaro almas hinib turuvchi ikki
izotermik va ikki adiabatik jarayondan iborat qaytar aylanma issiqlik
jarayonidir. (6.4-rasm).
pKarno sikli
– navbatma-navbat oʻzaro almas hinib turuvchi ikki
izotermik va ikki adiabatik jarayondan iborat qaytar aylanma issiqlik
jarayonidir. (6.4-rasm).
Karno sikli deb ataladigan ikkita izotermik va ikkita adiabatik jarayonlardan iborat siklni 6.5-rasmda keltirilgan kolenchatli val va shatun
1. Silindrdagi porshen eng pastki holatida,
gaz hajmi V1 ni tashkil etadi. Silindrni T1 temperaturali isitkichli idishga joylashtirilgan. Boshlang‘ich holatdagi gazning temperaturasi T1, bosimi p1 va hajmi V1 bo‘lsin, ushbu jarayonni 6.4-rasmdagi pV diagrammada gazning boshlang‘ich holatini 1 deb belgilaymiz. T1 temperaturali isitkichdan silindrga Q1 issiqlik miqdori beriladi va gazning isitkgichdan olayotgan issiqlik miqdori hisobiga uning izotermik ravishda hajmi V2 gacha kengayishi amalga oshadi. Nihoyat, gazning ikkinchi holatdagi parametrlari p2, V2, T1 bo‘ladi. Bu holatda gaz A1 ish bajaradi. 6.4-rasmdagi pV diagrammada gazning izotermik kengayishi 1–2 izoterma bilan ko‘rsatilgan.
2. Kengayishning ikkinchi adiabatik bosqichida Q1 issiqlik miqdori kamaytirilsa-da, porshen V2 dan V3 gacha kengayadi. Gaz ichki energiyasi hisobiga porshen A2 ish bajariladi, gazning temperaturasi pasayadi.
6.4-rasmdagi pV diagrammada gazning adiabatik kengayishi 2–3 adiabata bilan ko‘rsatilgan, gazning bu holatdagi parametrlari p3, V3, T2 bo‘ladi.
Isitkich Sovutkich
6.5-rasm.
3. Gazning izotermik siqilishini amalga oshirish uchun silindr T2 sovutkichga joylashtiriladi va porshen siqiladi, gaz hajmi V3 dan V4 gacha kamaytirila boshlaydi. Bu jarayon izotermik bo‘lishi uchun A ish batamom issiqlikka aylanib, gaz Q2 issiqlik miqdorini sovutkichga uzatadi, 6.5-b rasmdagi pV diagrammada gazning izotermik siqilishi 3–4 izoterma bilan ko‘rsatilgan, gazning bu holatdagi parametrlari p4, V4, T2 bo‘ladi.
4. Siklning oxirgi qismida gaz adiabatik siqilib, porshen gaz hajmini V4 dan V1 gacha kamaytiradi. Bunda bajarilgan ish gaz temperaturasini boshlang‘ich darajasiga ko‘tarish uchun sarfl anadi va sistemaning ichki energiyasi ortadi. 6.5-rasmdagi pV diagrammada gazning adiabatik siqilishi 4–1 adiabata bilan ko‘rsatilgan, gazning bu holatdagi parametrlari p1, V1, T1 bo‘ladi, ya’ni boshlang‘ich holatdagi qiymatini egallaydi.
Shunday qilib, ideal gaz o‘zining dastlabki holatiga qaytadi va ichki energiyasini to‘la tiklaydi. Sikl davomida ideal gaz isitkichdan Q1 issiqlik miqdorini oladi va sovitkichga Q2 issiqlik miqdori beradi. Termodinamikaning birinchi qonuniga muvofi q, Q1 – Q2 issiqlik miqdori ish bajarishga sarfl anadi va bu ish son qiymati jihatidan sikl o‘rab turgan yuzaga teng.
Issiqlik mashinasining foydali ish koeffi tsiyenti. Issiqlik mashinasining yoki Karno siklining foydali ish koeffi tsiyenti (FIK) deb quyidagi kattalikka aytiladi:
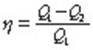 . (6.4) Agar
issiqlik mashinasining bajargan ishi hisobga olinsa, ya’ni A = Q1 – Q2 bo‘lsa, unda
. (6.4) Agar
issiqlik mashinasining bajargan ishi hisobga olinsa, ya’ni A = Q1 – Q2 bo‘lsa, unda
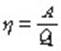 . (6.5)
. (6.5)
Shuningdek, Karno siklining FIK ni isitkichning T1 va sovitkichning T2 temperaturalari orqali ham ifodalash mumkin:
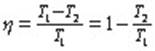 . (6.6)
. (6.6)
Demak, ideal issiqlik mashinasining FIK ishchi moddaning turiga bog‘liq bo‘lmay, balki isitkichning va sovitkichning temperaturalari bilangina aniqlanadi.
(6.6) ifodadan yana quyidagi xulosalarga kelish mumkin:
1) issiqlik mashinasining FIK ni ko‘tarish uchun isitkichning temperaturasini oshirish, sovitkichning temperaturasini esa pasaytirish kerak; 2) issiqlik mashinasining FIK doimo birdan kichik bo‘ladi.
(6.6) ga muvofi q Karno FIK to‘g‘risida teoremasini yozgan. Isitkichning va sovitkichning berilgan temperaturalarida istalgan dvigatelning FIK Karno siklining FIK dan katta bo‘lmaydi.
![]() 1. Issiqlik mashinasi deb qanday
qurilmaga aytiladi?
1. Issiqlik mashinasi deb qanday
qurilmaga aytiladi?
2. Karno sikli deb nimaga aytiladi?
3. Issiqlik mashinasining foydali ish koeffi tsiyenti (FIK) qanday aniqlanadi?
4. FIK ishchi moddaning turiga bog‘liqmi?
5. Issiqlik mashinasining FIK ni oshirish uchun nima qilish kerak?
![]()
Issiqlik dvigatellari. Issiqlik dvigatellariga bug‘ mashinasi, bug‘ turbinasi, ichki yonuv dvigateli, reaktiv dvigatellar kiradi.
Bug‘ mashinasi. Bug‘ mashinalari va bug‘ turbinalarida isitkich vazifasini bug‘ qozoni, ishchi modda vazifasini bug‘, sovitkich vazifasini esa atmosfera yoki ishlatilgan bug‘ni sovitish qurilmasi – kondensator bajaradi.
Ichki yonuv dvigateli. Ichki yonuv dvigatelida isitkich va ishchi modda vazifasini yonilg‘i, sovitkich vazifasini esa atmosfera o‘taydi.
Odatda, yonilg‘i sifatida benzin, spirt, kerosin va dizel yoqilg‘isi ishlatiladi. Maxsus qurilma (masalan, benzinli dvigatellarda karburator) yordamida yonilg‘i va havo aralashma ko‘rinishida tayyorlanib, silindrga uzati ladi. Silindrda esa aralashma yonadi. Yonish mahsulotlari esa atmos feraga chiqarib tashlanadi. Endi ba’zi turdagi dvigatellarga batafsil to‘xtalamiz.
Karburatorli dvigatel. To‘rt taktli karburatorli dvigatelning ish prinsipi va ishchi diagrammasini ko‘raylik (6.6-rasm). Tashqi kuchlar ta’sirida porshen pastga qarab harakatlanganda (6.6 a-rasm) kiritish klapani ochilib ishchi aralashma silindrga tushadi.
 0 V 0 V V 0 V
0 V 0 V V 0 V
a) b) d) e)
6.6-rasm.
Jarayon atmosfera bosimi ostida izobarik ravishda ro‘y beradi. Porshen eng quyi holatga yetganida kiritish klapani yopilib, birinchi takt (so‘rish takti) tugaydi: grafi kda jarayon 0–1 to‘g‘ri chiziq bilan ko‘rsatilgan. Ikkinchi (siqish) takti ham (6.6-b rasm) tashqi kuch ta’sirida ro‘y beradi.
Har ikkala klapan ham yopiq va gaz adiabatik ravishda qiziydi. Bu grafi kda 1–2 chiziqqa to‘g‘ri keladi. Uchinchi takt ish jarayonida chaqnab yonish (6.6-d rasm). Porshen eng yuqori holatga yetganida o‘t oldiruvchi svecha uchquni aralashmani yoqadi va gazning bosimi keskin ortadi. Grafi kda bu 2–3 izoxorik jarayonga mos keladi. Klapan yopiq turib, porshen pastga qarab harakatlanadi, ya’ni adiabatik ravishda kengayadi. 3–4 chiziq ishchi yo‘li taktiga to‘g‘ri keladi (6.6-d rasm). Ko‘rinib turibdiki, bu taktda gazning bosimi pasayadi, hajmi ortadi, temperaturasi pasayadi. Bu holda bajarilgan ish musbat bo‘lib, u gaz ichki energiyasining kamayishi hisobiga bajariladi. To‘rtinchi chiqarish takti 6.6-e rasmda tasvirlangan. Porshen eng pastga yetganida chiqarish klapani ochilib, yonish mahsulotlari chiqarish moslamasi orqali atrof-muhitga chiqarib tashlanadi. Gazning bosimi pasayadi va takt oxirida atmosfera bosimiga teng bo‘lib qoladi. Grafi kda bu izoxorik jarayon 4–1 chiziq bilan ko‘rsatilgan. Porshen maxovik energiyasi hisobiga yuqori holatiga qaytadi va takt tugaydi.
Ko‘rilgan yopiq jarayonda bajarilgan ish jarayonlar chiziqlari bilan ajratilgan, shtrixlangan shaklning yuzasiga teng bo‘ladi. Grafi kni tahlil qilish shuni ko‘rsatadiki, 3–4 qismdagi kengayish 1–2 qismdagi siqilishga nisbatan kattaroq bosimda ro‘y beradi. Aynan shuning natijasida dvigatel foydali ish bajaradi. 3–2 va 4–1 izoxorik jarayonlarda (V = const) ish nolga teng va yuqorida qayd etilganidek, foydali ish adiabatik kengayish va siqilishlarning farqlari bilan aniqlanadi.
Amalda ichki yonuv dvigatellarining FIK 20–30 % ni tashkil etadi. Ularning FIK ni orttirish uchun esa aralashmani ko‘proq siqish kerak. Lekin ichki yonish dvigatellarida yonilg‘i aralashmasini juda qattiq siqish mumkin emas, chunki siqilgan yonilg‘i qizib, o‘z-o‘zidan yonib ketishi mumkin. Bu esa dvigatelning ish prinsipini buzadi.
Dizel. Nemis muhandisi Dizel yuqoridagi qiyinchiliklardan holi va FIK ancha yuqori bo‘lgan dvigatelni yaratdi. Dizellarda siqish darajasi ancha yuqori bo‘lib, uning oxirida havoning temperaturasi, yoqilg‘i o‘z-o‘zidan o‘t olishi uchun yetarli darajada baland bo‘ladi. Yoqilg‘i esa karburatorli dvigatellarnikidek birdaniga emas, balki asta-sekin, porshen harakatining biror qismi davomida yonadi. Yoqilg‘ining yonish jarayoni ishchi bo‘shliqning hajmi ortib borishi davomida ro‘y beradi. Shuning uchun ham gazlarning bosimi ish davomida o‘zgarmay qoladi. Shunday qilib, dizelda aralashmaning yonish jarayoni o‘zgarmas bosimda ro‘y beradi. Karburatorli dvigatellarda esa bu jarayon o‘zgarmas hajmda ro‘y berar edi. Dizel, karburatorli dvigatelga qaraganda tejamkorroq bo‘lib, FIK ham ancha yuqori, qariyib 40 % ni tashkil qiladi. Uning quvvati ham ancha katta bo‘lishi mumkin. Shu bilan birga, ancha arzon yoqilg‘ida ham ishlayveradi. Dizellar statsionar qurilmalarda, temir yo‘l, havo va suv transportlarida keng qo‘llaniladi. Hozirgi paytda kichik quvvatli dizellar avtomashina va traktorlarda ham ko‘p ishlatilmoqda.
Reaktiv dvigatel. 6.7-rasmda reaktiv dvigatelning sxematik tuzilishi keltirilgan. Uning ish prinsipi quyidagicha. Samolyot uchganda qarshisidan kelayotgan havo oqimi soplo orqali o‘tib, forsunka sochayotgan yoqilg‘i bilan aralashib, ishchi yoqilg‘ini hosil qiladi. So‘ngra yonish kamerasiga tushadi va o‘t oldiruvchi svecha yordamida yonadi. Ishchi aralashmaning yonishi natijasida hosil bo‘lgan gazlar katta tezlik bilan chiqarish tirqishi – soplo orqali chiqarib tashlanadi. Aralashmaning yonishi bosimning keskin ortishiga olib keladi va natijada soplodan chiqadigan gazning tezligi dvigatelga kirayotgan gazning tezligidan juda katta bo‘ladi. Aynan shu tezliklar farqi natijasida impulsning saqlanish qonuniga muvofi q, reaktiv tortish kuchi vujudga keladi.
 Yoqilgi O‘t oldiruvchi svecha
Yoqilgi O‘t oldiruvchi svecha
6.7-rasm.
Hozirgi issiqlik mashinalarining FIK 40 % dan (ichki yonuv dvigatellari) 60 % gacha (reaktiv dvigatellar) bo‘lishi mumkin. Shuning uchun ham olimlar mavjud dvigatellarni takomillashtirish yo‘lida tinimsiz izlanishlar olib borishmoqda. Shu bilan birga, ichki yonuv dvigatellarining tinimsiz ko‘payib borayotganligi tabiatga va atrof-muhitga katta xavf tug‘dirmoqda. Ekologik toza dvigatellarni yaratish bugungi kunning eng dolzarb muammolaridan biridir.
Tabiatni muhofaza qilish. Tabiatning oliy mahsuli bo‘lmish inson, qolaversa boshqa jonzotlar ham shu tabiatning bir qismidir. Ular yashashi va rivojlanishi uchun esa zarur ne’matlar – toza havo, toza suv va toza mahsulotlar kerak. Biz nafas oladigan havo Yer atmosferasini tashkil qiluvchi gazlarning aralashmasidir. Uning tarkibida kislorod, azot, vodorod va boshqa tabiiy gazlardan tashqari chang, tutun, tuz zarralari va boshqa aralashmalar mavjud. Bundan tashqari, havo tarkibida sanoat chiqindilari ham bo‘ladi.
Issiqlik dvigatellarining ko‘p miqdorda ishlatilishi ham atrof-muhitga salbiy ta’sir ko‘rsatadi. Hisob-kitoblarga qaraganda, hozirgi paytda Yer yuzida har yili 2 milliard tonna ko‘mir va 1 milliard tonna neft yoqiladi. Bu esa Yerdagi temperaturaning ko‘tarilishiga va natijada muzliklarning erib, okeanlardagi suv sathining ko‘tarilishiga olib kelishi mumkin. Bundan tashqari, atmosferaga 120 million tonna kul va 60 million tonnagacha zaharli gaz chiqarib tashlanadi.
Dunyodagi 200 milliondan ortiq avtomobil har kuni atmosferani uglerod (II) oksid, azot va uglevodorodlar bilan zaharlaydi. Issiqlik va atom elektr stansiyalari quvvatlarining ortishi bilan suvga bo‘lgan ehtiyoj ham ortib boradi. Shuning uchun hozir havo va suv havzalarining ifl oslanishidan saqlanishning bevosita va bilvosita usullaridan foydalaniladi. Bevosita usul – bu turli tutunlar va gazlarni tozalab chiqarish; atmosferani kam ifl oslantiradigan yoqilg‘ilar – tabiiy gaz, oltingugurtsiz neft va boshqalardan foydalanish; benzinsiz yuradigan avtomobil dvigatellarini yaratish va hokazolar.
Bilvosita usullar atmosferaning pastki qatlamidagi zaharli moddalar konsentratsiyasining keskin kamayishiga olib keladi. Bular chiqindi chiquvchi manbalarning balandligini orttirish, meteorologik sharoitlarini hisobga olib aralashmalarni havoga sochib yuborishning turli usullaridan foydalanish va hokazolar.
![]() 1. Issiqlik dvigatellariga nimalar
kiradi?
1. Issiqlik dvigatellariga nimalar
kiradi?
2. Karburatorli dvigatelning ish prinsipini tushuntiring.
3. Ichki yonish dvigateli FIK ni oshirishning qanday qiyinchiligi bor?
4. Dizelning ish prinsipini tushuntiring.
5. Reaktiv dvigatelning ish prinsipini tushuntiring.
6. Tabiatni muhofaza qilish uchun qanday chora-tadbirlar ko‘rilmoqda?
Masala yechish namunasi
Foydali ish koeffi tsiyenti 0,4 ga teng bo‘lgan Karno siklida gazning izotermik ravishda kengayishda bajarilgan ish 8 J bo‘lsa, gazning izotermik ravishda siqilishidagi ish aniqlansin.
![]() B e r i l g a n: F o r m u l
a s i va y e c h i l i s h i: η = 0,4 Siklning pV – diagrammasini
tuzamiz η = 0,4; 1–2 A = 8 J o‘tish gazning izotermik kengayishini;
3–4 o‘tish esa T = const izotermik siqilishini ko‘rsatadi. Topish
kerak As
–?
B e r i l g a n: F o r m u l
a s i va y e c h i l i s h i: η = 0,4 Siklning pV – diagrammasini
tuzamiz η = 0,4; 1–2 A = 8 J o‘tish gazning izotermik kengayishini;
3–4 o‘tish esa T = const izotermik siqilishini ko‘rsatadi. Topish
kerak As
–?
Karno siklining FIK quyidagicha aniqlanadi:
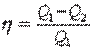 ,
,
bu yerda: Q1 – gazning isitkichdan olgan issiqlik miqdori, Q2 – gazning sovitkichga bergan issiqlik miqdori. Izotermik kengayishda bajarilgan Ak ish gazning isitkichdan olgan Q1 issiqlik miqdoriga, izotermik siqilishdagi As ish esa gazning sovitkichga bergan Q2 issiqlik miqdoriga teng bo‘ladi, ya’ni
Q1 = Ak; Q2 = As.
Unda siklning FIK quyidagi ko‘rinishni oladi:
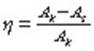 .
.
Bundan As ni topib, berilganlarni o‘rniga qo‘yib hisoblaymiz:
As = (1 – 0,4) ∙ 8 J = 4,8 J. Javobi: As = 4,8 J.
6-mashq
1. Temperaturasi 20 °C ga ortganda 200 g geliyning ichki energiyasi qanchaga o‘zgaradi? (Javobi: ΔU = 12,5 kJ).
2. 320 g kislorodni 10 K ga izobarik qizdirilganda qancha ish bajariladi? (Javobi: A = 830 J).
3. 15 °C temperaturali 1,5 kg suv bo‘lgan idishga 100 °C temperaturali 200 g suv bug‘i kiritildi. Bug‘ kondensatsiyalangandan keyin umumiy temperatura qanday bo‘ladi? (Javobi: t = 89 °C).
4. Massasi 290 g bo‘lgan havoni 20 K ga izobarik qizdirganda u qancha ish bajargan va bunda unga qancha issiqlik miqdori berilgan? (Javobi: 1,7 kJ; 5,8 kJ).
5. 800 mol gazni 500 K ga izobarik qizdirishda unga 9,4 MJ issiqlik miqdori berildi. Bunda gaz bajargan ishni va uning ichki energiyasi qancha ortganini aniqlang. (Javobi: 3,3 MJ; 6,1 MJ).
6. Temperaturasi 27° С bo‘lgan 160 g kislorod izobarik qizdirilganda uning hajmi ikki marta ortdi. Gazning kengayishida bajarilgan ishni, kislorodni qizdirishga ketgan issiqlik miqdorini, ichki energiya o‘zgarishini toping. (Javobi: 12,5 kJ; 44,2 kJ; 31,7 kJ).
7. Ideal issiqlik mashinasi qizdirgichining temperaturasi 117° C, sovitkichiniki 21° C. Mashinaning 1 s da qizdirgichdan olayotgan issiqlik miqdori 60 kJ ga teng. Mashinaning FIK ini, 1 s da sovitkichga berilayotgan issiqlik miqdorini va mashinaning quvvatini hisoblang. (Javobi: 23 %; 146 kJ; 14 kW).
8. Ideal issiqlik mashinasida qizdirgichdan olinayotgan har bir kilojoul energiya hisobiga 300 J ish bajariladi. Agar sovitkichning temperaturasi 280 K bo‘lsa, mashinaning FIK ini va qizdirgichning temperaturasini aniqlang. (Javobi: 30 %; 400 K).
9. 110 kW quvvatga erishadigan va bir soatda 28 kg dizel yonilg‘i sarfl aydigan traktor dvigatelining FIK ini toping. (Javobi: 34 %).
10. Agar mototsikl 108 km/soat tezlik bilan harakatlanib, 100 km yo‘l bosganida 3,7 l benzin sarfl ansa, dvigatelning FIK 25 % bo‘lsa, mototsikl dvigateli erishgan o‘rtacha quvvat qanday bo‘ladi? (Javobi: 8,9 kW).
1. Termodinamikaning birinchi qonunini ko‘rsating.
A) ΔU = Q + A; B) Q = ΔU + A; C) Q = ΔU – A; D) ΔU = Q – A.
2. Gapni to‘ldiring. Atrof-muhit bilan issiqlik miqdori almashmasdan ro‘y beradigan jarayonga ... jarayon deyiladi.
A) ... izotermik; B) .. izoxorik; C) ... adiabatik; D) ...izobarik.
3. Gapni to‘ldiring. Karno siklining foydali ish koeffi tsiyenti ...
A) ... birga teng; B) ... birdan katta; C) ... nolga teng; D) ... birdan kichik.
4. Issiqlik miqdori o‘z-o‘zidan past temperaturali jismdan yuqori temperaturali jismga o‘tmaydi. Bu ta’rif nimani ifodalaydi?
A) Termodinamikaning I qonuni; B) Termodinamik muvozanatni;
C) Termodinamikaning II qonuni; D) Termodinamik jarayon.
5. Gapni to‘ldiring. Yoqilg‘ining ichki energiyasini mexanik energiyaga aylantirib beradigan mashinaga ... deyiladi.
A) ... issiqlik dvigateli; B) ... issiqlik mashinasi;
C) ... reaktiv dvigateli; D) ... bug‘ turbinasi.
|
Termodinamik sistema |
O‘zaro va tashqi jismlar bilan ta’sirlashadigan hamda energiya almashadigan moddalar va jismlar majmuasi. |
|
Temperatura |
Makroskopik sistemaning termodinamik muvozanat holatini xarakterlovchi fi zik kattalik. |
|
Makroskopik sistema |
Juda ko‘p sondagi atom va molekulalardan tashkil topgan sistema. |
|
Termodinamik muvozanat |
Sistemaning makroskopik parametrlari ancha uzoq vaqtgacha o‘zgarmay turadigan jarayon. |
|
Termodinamik jarayon |
Termodinamik sistemaning hech bo‘lmaganda birorta parametrining o‘zgarishi. |
|
Qaytar jarayon |
Sistemaning oxirgi holatdan boshlang‘ich holatga o‘sha oraliq holatlar orqali, teskari yo‘nalishda atrof-muhitda hech qanday o‘zgarish ro‘y bermasdan o‘tishi. |
|
Qaytmas jarayon |
Ma’lum qarshilikka uchraydigan yoki issiq jismdan sovuq jismga issiqlik uzatish bilan ro‘y beradigan har qanday holat. |
|
Ichki energiya |
Moddaning barcha molekulalarning betartib harakat kinetik energiyalari va ularning o‘zaro ta’sir potensial energiyalarining yig‘indisi |
|
Termodinamika ning birinchi qonuni |
Q = ΔU + A Q – issiqlik miqdori; ∆U – ichki energiya o‘zgarishi; A – bajarilgan ish. |
|
Termodinamikaning ikkinchi qonuni |
Issiqlik miqdori o‘z-o‘zidan past temperaturali jism dan yuqori temperaturali jismga o‘tmaydi. |
|
Adiabatik jarayon |
Atrof-muhit bilan issiqlik miqdori almashmasdan ro‘y beradigan jarayon. |
|
Issiqlik mashinasi |
Yoqilg‘ining ichki energiyasini mexanik energiyaga aylantirib beradigan mashinalar. |
|
Aylanma jarayon yoki sikl |
Sistemaning bir qancha holatlardan o‘tib, o‘zining dastlabki holatiga qaytadigan jarayon. |
|
Karno sikli |
Navbatma-navbat oʻzaro almashinib turuvchi ikki izotermik va ikki adiabatik jarayonlardan iborat qaytar aylanma issiqlik jarayoni. |
|
Issiqlik mashinasining foydali ish koeffi tsiyenti |
|

![]()
![]() Zaryadlarning saqlanish qonuni. Jismlar
elektrlanganda ulardagi umumiy zaryad miqdori o‘zgaradimi? Bu savolga javob
topish uchun quyidagi tajribani o‘tkazaylik (7.1 a-rasm).
Zaryadlarning saqlanish qonuni. Jismlar
elektrlanganda ulardagi umumiy zaryad miqdori o‘zgaradimi? Bu savolga javob
topish uchun quyidagi tajribani o‘tkazaylik (7.1 a-rasm).
Elektrometr olib, uning sterjeniga metall b disk o‘rnatamiz. Disk ustiga qalin movut o‘rab, uning ustidan izolatsiya dastali boshqa diskni ishqalaylik. Bunda elektrometr
7.1-rasm. strelkasi og‘adi. Bu esa movutda va unga ishqalangan diskda elektr zaryadlari hosil
bo‘lganligini ko‘rsatadi.
Tajribani davom ettiramiz. Movutga ishqalangan diskni ikkinchi elektrometr sterjeniga tekkizamiz (7.1-b rasm). Bunda ikkinchi elektrometr strelkasi ham buriladi. Strelkaning og‘ish burchagi birinchi elektrometr strelkasining og‘ish burchagiga teng bo‘ladi. Bu esa har ikkala disk son qiymati jihatidan teng miqdorda zaryadlanganligini ko‘rsatadi. Agar har ikkala elektrometr sterjenlarini metall o‘tkazgich bilan tutashtirilsa, har ikkala elektrometr strelkasi nol holatga kelganligini ko‘ramiz. Bu hodisa elektrometrlar (disklar) son qiymati jihatidan teng, lekin ishoralari turlicha bo‘lgan zaryadga ega bo‘lganliklarini ko‘rsatadi. Shu sababli bu zaryadlarning yig‘indisi nolga teng chiqdi.
Elektrlanishga oid o‘tkazilgan barcha tajribalar shuni ko‘rsatadiki, yagona jismni zaryadlab bo‘lmas ekan. Jismni zaryadlash uchun albatta, ikkinchi jismning bo‘lishi shart. Elektrlanish jarayonida jismlardan biri qancha manfi y zaryad olsa, ikkinchisi shuncha miqdordagi musbat zaryadga ega bo‘ladi. Natijada jismlardagi umumiy zaryadlar miqdori o‘zgarishsiz saqlanadi. Har qanday yopiq sistema ichidagi barcha jismlar zaryadlarining algebraik yig‘indisi o‘zgarmaydi ya’ni:
q1 + q2 + ... +qn = const. (7.1)
Bu xulosa elektr zaryadining saqlanish qonuni deb ataladi.
Zaryadlarning saqlanish qonuni 1750-yilda amerikalik olim va siyosiy arbob Bendjamin Franklin tomonidan kiritilgan.
Faradey va Maksvell nazariyasiga ko‘ra zaryadlangan jismlar atrofi da elektr maydon hosil bo‘ladi. O‘zaro ta’sir shu elektr maydon vositasida amalga oshadi. Bu maydonni qo‘l bilan ushlab, ko‘z bilan ko‘rib bo‘lmaydi. Uni faqat ta’sirlariga ko‘ra sezish mumkin.
![]() Elektr maydonining zaryadli zarralarga ta’sirini o‘rganish
shuni ko‘rsatadiki, maydonning ta’siri zaryadlangan jism yaqinida kuchli, undan
uzoqlashgan sari kuchsizlanib boradi. Elektr zaryadlari hosil qilgan maydonning
kuchli yoki kuchsiz ekanligini ko‘rsatish uchun elektr maydon kuchlanganligi
deb ataluvchi kattalik kiritilgan. Elektr maydon kuchlanganligi
Elektr maydonining zaryadli zarralarga ta’sirini o‘rganish
shuni ko‘rsatadiki, maydonning ta’siri zaryadlangan jism yaqinida kuchli, undan
uzoqlashgan sari kuchsizlanib boradi. Elektr zaryadlari hosil qilgan maydonning
kuchli yoki kuchsiz ekanligini ko‘rsatish uchun elektr maydon kuchlanganligi
deb ataluvchi kattalik kiritilgan. Elektr maydon kuchlanganligi
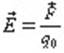 (7.2)
(7.2)
→ formula bilan aniqlanadi. Bunda E– maydonning biror nuqtasidagi maydon kuchlanganligi; → qo – maydonning shu nuqtasiga kiritilgan zaryad miqdori;
|F| – elektr maydoni tomonidan kiritilgan qo zaryadga ta’sir etuvchi kuch.
Elektr maydoni kuch chiziqlari yoki kuchlanganlik chiziqlari yordamida tavsifl anadi (7.2 va 7.3-rasmlar). Elektr maydon kuchlanganligi vektor kattalik bo‘lib, kuch chiziqlari yo‘nalishida bo‘ladi.

7.2-rasm. 7.3-rasm.
![]() Kuchlanganlik
birligi yoki 1 V .
Kuchlanganlik
birligi yoki 1 V .
m
Nuqtaviy q zaryadning r masofada hosil qilgan maydon kuchlanganligini hisoblaylik:
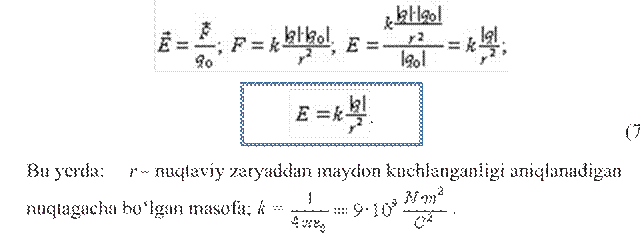
Elektr maydonini asosan zaryadlar tizimi hosil qiladi. Masalan, q1 va q2 zaryadlar tizimi hosil qilgan maydonning biror nuqtasiga sinov zaryadini kiritsak, unga har bir zaryad tomonidan F→1 va F→2 kuchlar ta’sir etadi (7.4rasm). Sinash zaryadiga ta’sir etayotgan bu kuchlarning teng ta’sir etuvchisi quydagiga teng bo‘ladi:
F→ = F→1 + F→2. (7.4)
U holda A nuqtadagi maydonning kuchlanganligi quyidagiga teng:
E→ = E→1 + E→2 . (7.5)
(7.5) ifoda quyidagicha ta’rifl anadi:
![]() Zaryadlar
sistemasining biror nuqtada hosil qilgan elektr maydon ining kuchlanganligi,
sistemaga kiruvchi har bir zaryadning o‘sha nuqtada alohida-alohida hosil
qilgan maydon kuchlang anliklarin ing vektor yig‘indisiga teng.
Zaryadlar
sistemasining biror nuqtada hosil qilgan elektr maydon ining kuchlanganligi,
sistemaga kiruvchi har bir zaryadning o‘sha nuqtada alohida-alohida hosil
qilgan maydon kuchlang anliklarin ing vektor yig‘indisiga teng.
E→ = E→1 + E→2 + E→3 + ... + E→n. (7.6)
Bu elektr maydonning superpozitsiya prinsipi deyiladi.
Superpozitsiya so‘zining lug‘aviy ma’nosi “qo‘shilish yoki ustma-ust tushish” degan ma’noni anglatadi.
Superpozitsiya prinsipiga ko‘ra bir-biridan r masofada
joylashgan ikki nuqtaviy zaryadning biror nuqtadagi maydon kuchlanganligini
hisoblaylik (7.4-rasm). Har bir zaryadning qaralayotgan nuqtadagi maydon
kuchlanganligi  va
va  ifodalarga ko‘ra
aniqlanadi.
ifodalarga ko‘ra
aniqlanadi.
Zaryadlarning shu nuqtadagi natijaviy maydon kuchlanganligi superp ozitsiya prinsipiga asosan quyidagi ifoda asosida hisoblanadi:
![]()
![]() . (7.7)
. (7.7)
Bu yerda: E1 va E2 mos ravishda nuqtaviy zaryadlarning qaralayotgan nuqtadagi maydon kuchlanganliklari, α – maydon kuchlanganlik vektorlari orasidagi burchak.
Masala yechish namunasi q1 >0 q2 >0 Zaryadlari 4 nC dan bo‘lgan ikkita qarama 7.4-rasm.
qarshi ishorada zaryadlangan nuqtaviy zaryadlar bir-biridan 10 sm masofada joylashgan. Birinchi zaryaddan 8 sm, ikkinchi zaryaddan 6 sm masofada joylashgan nuqtadagi maydon kuchlanganligi nimaga teng?
 Fo r m u l a s i v a y e c h i l i
s h i:
Fo r m u l a s i v a y e c h i l i
s h i:
![]() 1.
Nuqtaviy zaryadning kuzatilayotgan nuqtadagi maydon kuchlanganligi qanday
hisoblanadi?
1.
Nuqtaviy zaryadning kuzatilayotgan nuqtadagi maydon kuchlanganligi qanday
hisoblanadi?
2. Superpozitsiya so‘zining ma’nosi nima?
3. Superpozitsiya prinsipini ta’rifl ang va uning formulasini yozing.
![]()
Radiusi R ga teng bo‘lgan elektr o‘tkazuvchi shar q zaryad bilan zaryadlangan bo‘lsin (7.5-a rasm). Zaryadlangan bunday shar (sfera) ning hosil qilayotgan elektr maydon kuchlanganligini uning markazida, sirtida va undan tashqarisida aniqlaylik. Buning uchun biz dastlab q zaryadni sirt bo‘ylab tekis taqsimlangan bir qancha bir xil miqdordagi zaryadlarga ajratamiz, ya’ni q = q1 + q2 + q3 + ... + q'1 + q'2 + q'3...
Har qanday miqdori bir xil bo‘lgan q1 va q'1 kabi zaryadlarning sharning markazidagi natijaviy maydoni kuchlanganligi superpozitsiya prinsipiga ko‘ra nolga teng bo‘ladi Demak, zaryadlangan sferaning ichida maydon kuchlanganligi nolga teng bo‘ladi.
Shardan tashqarida undan r masofada joylashgan ixtiyoriy A nuqtadagi maydon kuchlanganligini topaylik. OA chiziqqa simmetrik joylashgan q2 va q'2 zaryadlar juftini ajratib olaylik. Bu zaryadlar Or o‘qi boylab yo‘nalgan o‘qda kuchlanganlik hosil qiladi. Demak, shar tashqarisidagi nuqtadagi maydon kuchlanganligining kuch chiziqlari, shar markaziga qo‘yilgan musbat zaryadlangan nuqtaviy zaryad maydonining kuch chiziqlari bilan mos tushadi (7.5-b, rasm).
a) b) c)
7.5-rasm.
Zaryadlangan sharning sirtidagi elekrt maydon kuchlanganligi quyidagicha aniqlanadi.
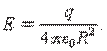
Zaryadlangan shar tashqarisidagi nuqtada hosil qilingan maydon kuchlan ganligi bilan nuqtaviy zaryad hosil qilgan maydon bir xilligidan shar tashqarisidagi (r ≥ R) nuqtada hosil qilingan maydon kuchlanganligini quyidagi formuladan hisoblash mumkin:
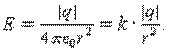 (7.6)
(7.6)
Bunga ko‘ra shar sirtidan uzoqlashgan sari maydon kuchlanganligi masofa kvadratiga teskari proporsional ravishda kamayib boradi (7.5-c rasm).
Elektr maydon kuchlanganligi maydon hosil qiluvchi zaryad joylashgan muhitning xossalariga bog‘liq. Qarama-qarshi ishorada zaryadlangan ikkita plastina oralig‘iga dielektrik kiritilgan holni qaraylik (7.6-rasm).
|
0 → → → maydon E = E0 – E' gacha susayadi. Dielektrik tufayli maydonning necha marta susayganligini ko‘rsatadigan kattalikka dielektrikning dielektrik singdiruvchanligi deyiladi: |
–q' +q' 7.6-rasm. |
|
|
(7.7) |
![]() Dielektrikda erkin elektronlar juda kam. Asosiy
elektronlar atom elektron qobigida joylashadi. Plastinadagi elektr
zaryadlarining maydoni ta’sirida elektron qobiq deformatsiyalanadi. Natijada
atomdagi musbat va manfi y zaryadlarning markazlari ustma-ust tushmaydi. Bu
hodisaga ± – dielektrikning
qutblanishi deyiladi.
Dielektrikda erkin elektronlar juda kam. Asosiy
elektronlar atom elektron qobigida joylashadi. Plastinadagi elektr
zaryadlarining maydoni ta’sirida elektron qobiq deformatsiyalanadi. Natijada
atomdagi musbat va manfi y zaryadlarning markazlari ustma-ust tushmaydi. Bu
hodisaga ± – dielektrikning
qutblanishi deyiladi.
Qutblangan atomlar (molekulalar) ning hosil qilgan maydon kuchlanganligi E→', asosiy maydon kuchlanganligi E→ ga qarama-qarshi yo‘nalgan bo‘ladi. Natijada umumiy
U holda, dielektrik ichida joylashtirilgan nuqtaviy zaryaddan r masofada turgan nuqtadagi maydon kuchlanganligi ham ε marta kamayadi:
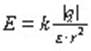 . (7.8)
. (7.8)
Shuningdek, bir jinsli dielektrik ichida joylashgan nuqtaviy zaryadlar orasidagi o‘zaro ta’sir kuchi vakuumdagi ta’sir kuchidan ε marta kichik bo‘ladi va bu ta’sir kuchi quyidagi ifoda yordamida hisoblanadi:
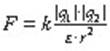 . (7.9)
. (7.9)
Dielektrik singdiruvchanlik o‘lchamsiz kattalikdir.
![]() 1. Nima
sababdan zaryadlangan sharning ichida elektr maydoni nolga teng bo‘ladi?
1. Nima
sababdan zaryadlangan sharning ichida elektr maydoni nolga teng bo‘ladi?
2. Zaryadlangan sharning sirtida va tashqarisida elektr maydoni qanday hisoblanadi?
3. Nima sababdan dielektrik moddalar elektr maydonini susaytiradi?
![]()
Elektr maydonining kuchli yoki kuchsiz ekanligini aniqlash uchun uning maydoniga sinash zaryadi kiritilib, maydon tomonidan unga qanday kuch ta’sir etishi aniqlangan edi. Shuning uchun ham elektr maydon kuchlanganligi maydonning kuch xarakteristikasi hisoblanadi.
![]() Maydonga sinov zaryadi olib kirilishiga asosiy zaryad
maydoni qarshilik qiladi (7.7-rasm). Shunga ko‘ra maydon kuchlariga qarshi ish
bajarish lozim bo‘ladi.
Maydonga sinov zaryadi olib kirilishiga asosiy zaryad
maydoni qarshilik qiladi (7.7-rasm). Shunga ko‘ra maydon kuchlariga qarshi ish
bajarish lozim bo‘ladi.
Bu bajarilgan ish qanday aniqlanadi?
Bu ish asosiy zaryad va kiritilgan sinov zaryad ining o‘zato ta’sir potensial energiyasiga aylanadi:
![]() .
(7.9)
.
(7.9)
Formulada minus ishora qo‘yilishi, zaryadlar orasida tortishish kuchi ta’sir qilishini ko‘rsatadi.
7.7-rasm.
Qo‘zg‘almas Q musbat zaryaddan r masofada turgan +q zaryadning potensial energiyasi quyidagicha ifodalanadi:
![]() . (7.10)
. (7.10)
Formulada musbat ishora qo‘yilishi, zaryadlar orasida itarishish kuchi ta’sir qilishini ko‘rsatadi.
Potensial energiyaning nol hisobi sifatida formulaga ko‘ra cheksiz katta masofa olinadi. Bunday masofada zaryadlar o‘zaro ta’sirlashmaydi.
Shunday qilib, elektr maydoni kuch xarakteristikasiga ega bo‘lishi bilan birga energetik xarakteristikaga ega bo‘ladi. U elektr maydoni potensiali deb ataluvchi kattalik orqali ifodalanadi.
Nuqtaviy zaryadning elektr maydoni potensiali deyilganda asosiy va maydonga kiritilgan sinov zaryadlari o‘zaro ta’sir potensial energiyasini sinov zaryadi miqdoriga nisbati bilan o‘lchanadigan kattalikka aytiladi:
φ
= ![]() . (7–11)
. (7–11)
Nuqtaviy q zaryadning potensiali quyidagicha aniqlanadi:
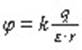 .
(7.12)
.
(7.12)
Potensial tushunchasidan foydalanib, q1 zaryadni maydon hosil qiluvchi q zaryaddan r1 uzoqlikdagi nuqtadan r2 uzoqlikdagi nuqtaga ko‘chirishda bajarilgan ishni topamiz:
A = W1 – W2 yoki 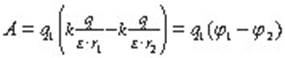 . (7.13)
. (7.13)
![]() Bu ifodadagi φ1 – φ2 ayirma nuqtalar orasidagi potensiallar
farqidan iborat bo‘lib, unga elektr kuchlanish deyiladi
va quyidagi ko‘rinishda yoziladi:
Bu ifodadagi φ1 – φ2 ayirma nuqtalar orasidagi potensiallar
farqidan iborat bo‘lib, unga elektr kuchlanish deyiladi
va quyidagi ko‘rinishda yoziladi:
U = φ1 – φ2. (7.14)
|
atrofi da konsentrik aylanalar shaklida joylashadi (7.8rasm). Maydon kuch chiziqlari ekvipotensial sirtga doimo perpendikulyar bo‘ladi. |
E1>E2, φ1<φ2 7.8-rasm. |
![]() Potensial va potensiallar ayirmasining birligi italyan
olimi Voltaning sharafi ga Volt (V) deb ataladi. φ =
Potensial va potensiallar ayirmasining birligi italyan
olimi Voltaning sharafi ga Volt (V) deb ataladi. φ = ![]() dan
dan
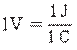 ga
teng. Ta’rifga ko‘ra
ga
teng. Ta’rifga ko‘ra
1C zaryadni elektr maydonning bir nuqtasidan ikkinchi nuqtasiga ko‘chirishda elektr maydoni 1 J ish bajaradigan nuqtalar potensiallarining ayirmasi 1 V ga teng bo‘ladi.
Nuqtaviy zaryaddan bir xil uzoqlikda joylashgan nuqtalarning potensiallari teng bo‘ladi. Agar ushbu nuqtalar birlashtirilib chiqilsa, hosil bo‘lgan sirt ekvipotensial sirt deyiladi.
Nuqtaviy zaryadning ekvipotensial sirti zaryad
Elektr maydon kuchlanganligi va potensiallar ayirmasi orasida quyidagi munosabat mavjud:
E
= ![]() , (7.15)
, (7.15)
d – potensiallari φ1 va φ2 bo‘lgan nuqtalar
orasidagi masofa. Bundan maydon kuchalanganligi birligi 1![]() kelib
chiqadi.
kelib
chiqadi.
Masala yechish namunasi
Havoda turgan 5 sm radiusli metall sferaga 30 nC zaryad berildi. Zaryadlangan sfera markazidan 2 sm, sfera sirtida va sfera sirtidan 5 sm uzoqlikdagi nuqtadagi maydon potensiali topilsin.
![]()
![]()
![]() B
e r i l g a n: Y e c h i l i s h i: q= 30 nC = 30 · 10–9C φichida
B
e r i l g a n: Y e c h i l i s h i: q= 30 nC = 30 · 10–9C φichida
r = 5 sm = 5 · 10–2 mφichida = φsirtida= 9 · 10 ; r1= 2 sm = 2 · 10–2 m
r2= 5 sm = 5 · 10–2 m φ φtashqarisida = 9 · 109 · k = 9 · 109 N · m2/C2=2700 V.
=
Topish kerakBirligi:
![]() φichida – ? φsirtida – ?[φ] = . φtashqarida – ?
φichida – ? φsirtida – ?[φ] = . φtashqarida – ?
Javobi: 5400 V; 2700 V.
1.
![]() Elektrostatik kuchning bajargan ishi bilan maydonda
ko‘chayotgan zaryad potensial energiyasi orasidagi bog‘lanishni yozing.
Elektrostatik kuchning bajargan ishi bilan maydonda
ko‘chayotgan zaryad potensial energiyasi orasidagi bog‘lanishni yozing.
2. Elektr maydonida turgan zaryadning potensial energiyasi qanday aniqlanadi?
3. Protondan 5,3 · 10–11 m uzoqlikdagi elektr maydon potensialini toping. Protondan mana shunday uzoqlikda joylashgan orbita bo‘ylab harakatlanayotgan elektronning potensial energiyasi nimaga teng bo‘ladi?
![]()
Mexanikada kiritilgan fi zik kattaliklar (ko‘chish, kuch, kuchning bajargan ishi, potensial energiya) istalgan fundamental o‘zaro ta’sirlarni, shu jumladan, elektromagnit ta’sirlarni ifodalashda foydalaniladi.
Yerning bir jinsli (g = const) gravitatsion maydonida jismni g→ bo‘ylab h masofaga ko‘chirishda (7.9-rasm) og‘irlik kuchining bajargan ishi A = mgh edi.
A = mgh A = qEh
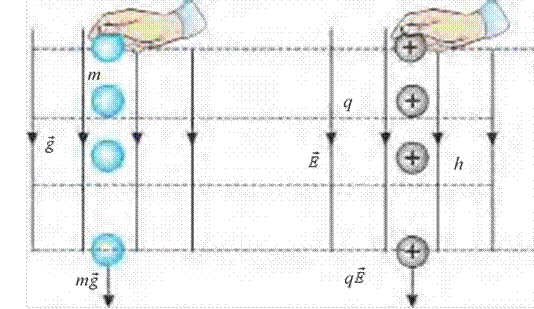
7.9-rasm
+q zaryadni bir jinsli (E→ = const) elektr maydon kuch chiziqlari bo‘ylab ko‘chirishda bajarilgan ish
Aq = qEh (7.16)
ga teng bo‘ladi. Bu formula elektr maydon kuchlanganligi bilan ko‘chish yo‘nalishi mos kelganda o‘rinli bo‘ladi.
Ularning yo‘nalishi mos kelmaydigan holni ham qaraylik.
Bir jinsli elektr maydoniga kiritilgan zaryad q (q > 0, bo‘lganda) elektr maydon yo‘nalishida yoki unga teskari yo‘nalishda (q < 0, bo‘lganda) ko‘chshganda elektr maydoni ish bajaradi. Ishni hisoblash uchun dastlab X o‘qini maydon kuchlanganligi bilan bir yo‘nalishda tanlaymiz (7.10-rasm).
![]()
![]() Musbat ishorali zaryadga maydon tomonidan ta’sir etayotgan kuch ham X
o‘qi bilan bir tomonga yo‘nalgan bo‘ladi. Maydondagi zaryad = q kuch
ta’sirida s yo‘l bo‘ylab N nuqtadan M nuqtaga ko‘chgan
bo‘lsa, uni ko‘chirishda elektr kuchining bajargan ishi quyidagicha aniqlanadi:
Musbat ishorali zaryadga maydon tomonidan ta’sir etayotgan kuch ham X
o‘qi bilan bir tomonga yo‘nalgan bo‘ladi. Maydondagi zaryad = q kuch
ta’sirida s yo‘l bo‘ylab N nuqtadan M nuqtaga ko‘chgan
bo‘lsa, uni ko‘chirishda elektr kuchining bajargan ishi quyidagicha aniqlanadi:
A=F · s · cosα = q · E · s · cosα. (7.17)
7.10-rasm. Bu yerda: α – kuch bilan ko‘chish orasidagi burchak.
Δx = x2 – x1 = s · cosα ekanligidan (7.17) tenglik quyidagi ko‘rinishga keladi:
A = qEΔx. (7.18)
Endi elektrostatik maydonda q zaryadni NBM siniq chiziq bo‘ylab ko‘chirishda bajarilgan ishni hisoblaylik. Ish skalyar kattalik bo‘lganligi uchun NBM yo‘lda bajarilgan ish NB va BM yo‘llarda bajarilgan ishlarning algebraik yig‘indisiga teng bo‘ladi A = A1 + A2.
Zaryadni ko‘chirishdagi A1 va A2 ishlar xuddi zaryadni NM yo‘l bo‘ylab ko‘chirishda bajarilgan ish kabi aniqlanadi, ya’ni:
A1 = qEΔx1 va A2 = qEΔx2. (7.19)
Δx1 va Δx2 mos ravishda s1 va s2 ko‘chish vektorlarining X o‘qdagi proeksiyalari. U holda (7.18) ga (7.19) ifoda qo‘yilsa, quyidagi ko‘rinishga keladi:
A = qE(Δx1+ ∆x2) = qEΔx.
Bundan quyidagi xulosa kelib chiqadi. Bir jinsli elektr maydonida zaryadni ko‘chirishda bajarilgan ish ko‘chish yo‘lining shakliga bog‘liq bo‘lmay, faqat zaryad ko‘chgan nuqtalarning boshlang‘ich va oxirgi vaziyatlari (ya’ni Δx) ga bog‘liq bo‘ladi, bunday maydon potensial maydon deyiladi. Demak, elektrostatik maydon – potensial maydon ekan. Shuning uchun elektrostatik maydonda zaryadni yopiq kontur bo‘ylab ko‘chirishda bajarilgan ish doimo nolga teng bo‘ladi. Bajargan ishi zaryadning harakat trayektoriyasiga bog‘liq bo‘lmagan kuchga konservativ kuch deyiladi. E · Δx = φ2 – φ1 ekanligi hisobga olinsa,
A = q(U2 – U1) (7.20) ga ega bo‘lamiz. Bu formula q elektr zaryadini elektr maydonida potensiali φ2 bo‘lgan nuqtadan potensiali φ1 bo‘lgan nuqtaga ko‘chirishda bajarilgan ishni hisoblash formulasidir.
Masala yechish namunasi
100 μC zaryad nuqtaviy zaryad maydon kuchlanganligi 4 kV/m bo‘lgan bir jinsli elektr maydonda 4 sm masofaga ko‘chganda elektrostatik maydon 8 mJ ish bajardi. Maydon kuch chiziqlari va ko‘chish vektori orasidagi burchak qanday bo‘lgan?
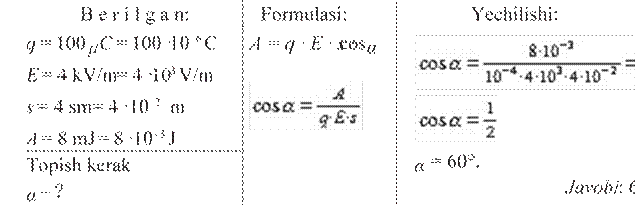
1.
![]() Potensial maydon deb qanday maydonga aytiladi?
Potensial maydon deb qanday maydonga aytiladi?
2. Elektrostatik maydonda zaryadni yopiq chiziq bo‘ylab ko‘chirishda bajarilgan ish nimaga teng?
3. 7.20 formuladan foydalanib potensiallar ayirmasiga ta’rif bering.
![]()
O‘tkazgichni zaryadlash uchun zaryadlar orasidagi o‘zaro itarish kuchini yengishda ish bajariladi. Bu ish hisobiga, o‘tkazgich energiyaga ega bo‘ladi. Zaryadlangan jismning olgan energiyasi miqdor jihatdan (Wel – bu energiya elektr maydon energiyasi deb ataladi) uni zaryadlashda bajarilgan ishning miqdoriga aynan teng bo‘ladi, ya’ni A = Wel. O‘tkazgichni zaryadlashda bajarilgan ish qanday hisoblanadi? Dastlab jism zaryadlanmagan bo‘lsa, uning potensiali nolga teng bo‘ladi. Unga q zaryad berilsa, uning potensiali noldan φ gacha o‘zgaradi. Jismni zaryadlashda bajarilgan ish:
A = q · φo‘rt (7.21) ga teng bo‘ladi. Jism poten sialining o‘rtacha qiymati uning boshlang‘ich va oxirgi qiymatlarining o‘rta arifmetik qiymatiga teng bo‘ladi, ya’ni
φo‘rt![]() (7.22) φo‘rt ning qiymatini
(7.21) tenglikka qo‘yib, qo‘yidagi ifodani hosil qilamiz:
(7.22) φo‘rt ning qiymatini
(7.21) tenglikka qo‘yib, qo‘yidagi ifodani hosil qilamiz:
![]() . (7.23)
. (7.23)
Demak, jismni zaryadlashda bajarilgan ish uning zaryadi bilan
potensiali ko‘paytmasining yarmiga teng bo‘lar ekan. Jismni zaryadlashda uning
potensiali ![]() formulaga binoan tekis, ya’ni chiziqli
o‘zgaradi. Bunda C – o‘tkazgichning elektr sig‘imi. U holda (7.23)
ifodani
formulaga binoan tekis, ya’ni chiziqli
o‘zgaradi. Bunda C – o‘tkazgichning elektr sig‘imi. U holda (7.23)
ifodani
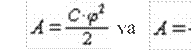 (7.24)
(7.24)
ko‘rinishlarda yozish mumkin. Jumladan, A = Wel munosabatga ko‘ra yakkalangan zaryadlangan jismning elektr maydon energiyasini quyidagicha yozamiz:
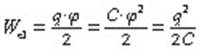 .
(7.25)
.
(7.25)
Agar zaryadlangan jism kondensatordan iborat bo‘lsa, uning elektr maydon energiyasini (Wkon) hisoblashda (7.25) ifodadagi zaryad miqdorini kondensatorning bitta qoplamasidagi zaryad miqdori bilan, potensialini esa uning qoplamalari orasidagi potensiallar ayirmasi bilan almashtirish lozim, ya’ni:
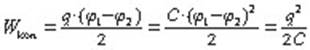 (7.26)
(7.26)
bo‘lganligi uchun zaryadlangan kondensatorning elektr energiyasini aniqlash formulasini
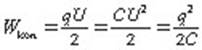 (7.27) ko‘rinishlarda yozish mumkin
(7.27) ko‘rinishlarda yozish mumkin
Zaryadlangan jismning energiyasi uning atrofi da hosil bo‘lgan elektr maydonida mujassamlangan bo‘lib, energiyaning qiymati elektr maydoni tarqalgan fazoning hajmiga va maydonning kuchlanganligiga bog‘liq bo‘ladi. Xususiy holda zaryadlangan yassi kondensatorni qarab chiqaylik. Yassi kondensator qoplamalaridagi zaryadlar hosil qilgan elektr maydoni uning qoplamalari orasidagi muhitda mujassamlashgan bo‘ladi. Fazoning hajmini V = Sd formula orqali hisoblash mumkin.
Zaryadlangan yassi kondensatorning sig‘imi ![]() va
kondensator maydon kuchlanganligi bilan qoplamalari orasidagi potensiallar
farqi orasidagi bog‘lanish hamda (7.27) formulaga binoan quyidagiga ega
bo‘lamiz:
va
kondensator maydon kuchlanganligi bilan qoplamalari orasidagi potensiallar
farqi orasidagi bog‘lanish hamda (7.27) formulaga binoan quyidagiga ega
bo‘lamiz:
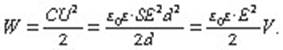 (7.28)
(7.28)
Zaryadlangan yassi kondensatorning energiyasi uning hosil qilgan elektr maydoni kuchlanganligining kvadratiga va shu maydon egallagan fazoning hajmiga to‘g‘ri proporsional ekan. Maydonning hajm birligiga to‘g‘ri kelgan energiyasi energiyaning hajmiy zichligi deyiladi. Ta’rifga ko‘ra:
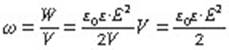 . (7.29)
. (7.29)
Har bir kondensator nafaqat o‘zida zaryad to‘plash, shuningdek, energiya to‘plash xususiyatiga ham ega. Kondensator olgan energiya qoplamalar orasidagi muhutda bo‘ladi. Bu energiyani kondensatorda uzoq vaqt davomida saqlab bo‘lmaydi. Kondensator olgan zaryadini vaqt o‘tishi bilan uni o‘rab turgan atrof muhitga uzatadi.
Kondensator elektr qarshiligi kichik bo‘lgan zanjir orqali zaryadsizlanganda, o‘z energiyasini deyarli bir zumda beradi.
Masala yechish namunasi
Yassi havo kondensatorining sigimi 0,1 μF teng bo‘lib, 200 V potensiallar farqiga ega. Kondensatordagi elektr maydon energiyasini hisoblang.
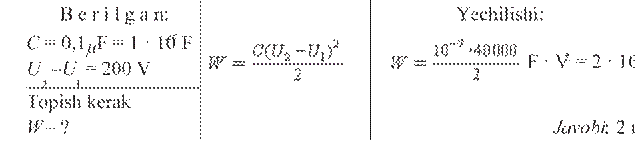 F o r m u l a s i:
F o r m u l a s i:
1.
![]() Zaryadlangan jismning olgan energiyasi qanday
kattaliklarga bog‘liq?
Zaryadlangan jismning olgan energiyasi qanday
kattaliklarga bog‘liq?
2. Kondensatorni zaryadlashda qanday ish bajariladi?
3. Zaryadlangan kondensator energiyasi qayerda to‘planadi?
7-mashq
1. Tomonlari 10 sm bo‘lgan muntazam uchburchakning ikki uchida – 4 nC va + 4 nC bo‘lgan ikki zaryad joylashgan. Uchburchakning uchinchi uchidagi maydon kuchlanganligi nimaga teng? (Javobi: 3,6 kV/m).
2. Dielektrik muhit ichida bir-biridan 6 sm masofada zaryadi 6 nC va –8 nC bo‘lgan ikki zaryad joylashgan. Ular o‘rtasidagi maydon kuchlanganligi qanday? (Javobi: 140kV/m).
3. Qanday nuqtaviy zaryad potensiallar farqi 100 V bo‘lgan ikki nuqta orasida ko‘chirilganda, maydon 5 μJ ish bajaradi? (Javobi: 50 nC).
4. Elektrostatik maydonning biror nuqtasidagi 50nC zaryad 7,5 μJ potensial energiyaga ega. Shu nuqtadagi elektr maydon potensialini toping. (Javobi: 150 V).
5. Ikkita +0,4 μC va −0,6 μC nuqtaviy zaryadlar bir-biridan 12 sm masofada joylashgan. Zaryadlarni tutashtiruvchi kesma o‘rtasida elektr maydon potensiali qanday bo‘ladi? (Javobi: –30 kV).
6. Zaryadi 3 · 10–8 C ga teng bo‘lgan ikki nuqtaviy zaryad havoda birbiridan 50 sm masofada turibdi. Ularni 20 sm gacha yaqinlashtirish uchun qanday ish bajarilishi kerak? (Javobi: 10,8 μJ).
7. Agar zaryadlangan ikkita parallel plastinka orasidagi masofa 12 sm, potensiallar ayirmasi 180 V bo‘lsa, plastinkalar orasidagi maydon kuchlanganligini aniqlang. (Javobi: 1500 V/m).
8. Kuchlanganligi 6000 V/m bo‘lgan bir jinsli elektr maydonda bitta kuchlanganlik chizig‘ida olingan, orasidagi masofa 2 sm bo‘lgan ikki nuqta orasidagi potensiallar farqi qanday bo‘ladi? (Javobi: 120 V).
9. Yassi kondensator qoplamalaridagi kuchlanish 150 V, zaryadi 80 μC bo‘lsa, kondensatordagi maydon energiyasi nimaga teng? (Javobi: 6 mJ).
10. Yassi kondensator 2 μC zaryad olib, 0,5 μJ maydon energiyasiga ega bo‘ldi. Kondensator sig‘imi qanday bo‘lgan? (Javobi: 16 μF).
11. Yassi kondensatorga 4 · 10−5 C zaryad berilganda, uning energiyasi 20 mJ ga teng bo‘ldi. Kondensator qoplamalari orasidagi kuchlanish qanday bo‘lgan? (Javobi: 1000 V).
12. Dielektrik singdiruvchanligi 4 va kuchlanganligi 3 · 103 V/m bo‘lgan nuqtadagi elektr maydonning energiya zichligini toping. (Javobi: 159 μJ/m3).
1. Maydon kuchlanganligi 800 V/m bo‘lgan nuqtaga joylashgan 5 μC zaryadga qancha elektrostatik kuch (N) ta’sir qiladi?
A) 4 · 10-2; B) 4 · 10−3; C) 3,2 · 10−5; D) 1,6 · 10−5.
2. Kuchlanganligi 27,3 kV/m bo‘lgan elektr maydonda hara kat qilayotgan elektronning tezlanishi nimaga teng (m/s2)? me = 9,1 · 10−31 kg.
A) 4,8 · 1016; B) 4,8 · 1015; C) 7,2 · 1016; D) 9,6 · 1015.
3. 1 · 10−4 g massali zaryadlangan tomchi, kuchlanganligi 100 N/C bo‘lgan bir jinsli elektr maydonda muvozanatda turibdi. Tomchining zaryadini aniqlang (C).
A) 10−8; B) 10−6; C) 10−4; D) 10−3.
4. Radiusi 2 sm bo‘lgan metall sharga 1,2 nC zaryad berildi. Shar sirti yaqinidagi elektr maydon kuchlanganligini toping (kV/m).
A) 27; B) 18; C) 24; D) 9.
5. Radiusi 6 sm bo‘lgan metall sharga 24 nC zaryad berilgan. Shar markazidan 3 sm uzoqlikdagi nuqtada kuchlanganlik qanchaga teng bo‘ladi (kV/m)?
A) 45; B) 90; C) 60; D) 0.
6. Radiusi 12 sm bo‘lgan sharning sirtida 0,18 μC musbat zaryad tekis taqsimlangan. Sharning markazidagi maydon potensialini toping (V).
A) 90; B) 60; C) 120; D) 180.
7. Ikkita nuqtaviy zaryad orasidagi masofani 9 marta kamaytirsak, ularning o‘zaro ta’sir potensial energiyasi qanday o‘zgaradi?
A) 9 marta ortadi; B) 9 marta kamayadi; C) 3 marta ortadi; D) 3 marta kamayadi.
8. Nuqtaviy q zaryad potensiallar farqi 100 V bo‘lgan ikki nuqta orasida ko‘chirilganda, 5 mJ ish bajarilgan. q zaryad kattaligi (μC) qanday bo‘lgan?
A) 20; B) 5; C) 500; D) 50.
|
Zaryadlarning saqlanish qonuni |
Har qanday yopiq sistema ichidagi barcha jismlar zaryadlarining algebraik yig‘indisi o‘zgarmaydi ya’ni: q1 + q2 + ... +qn = const. |
|
Elektr maydonining kuch chiziqlari |
Elektr maydoniga kiritilgan musbat zaryadga maydon tomonidan ta’sir etuvchi kuch yo‘nalishini ko‘rsatuvchi chiziqlar. Musbat zaryad hosil qilgan elektr maydon kuch chiziqlari zaryaddan chiquvchi, manfi y zaryadniki esa zaryadga kiruvchi bo‘ladi. |
|
Elektr maydon kuchlanganligi |
zaryadga maydon tomonidan ta’sir etuvchi kuch. |
|
Nuqtaviy q zaryadning r masofada hosil qilgan maydon kuchlanganligi |
|
|
Elektr maydonning superpozitsiya prinsipi |
Zaryadlar sistemasining biror nuqtada hosil qilgan elektr maydonining kuchlanganligi, sistemaga kiruvchi har bir zaryadning o‘sha nuqtada alohidaalohida hosil qilgan maydon kuchlanganliklarining vektor yig‘indisiga teng:
|
|
Zaryadlangan shar (sfera) ichkarisida va sirtidagi nuqtalardagi hosil qilingan maydon kuchlanganligi |
E = 0;
|
|
Dielektrikning qutblanishi |
Elektr maydoniga joylashtirilgan modda (muhit) atomlari (molekulalari) elektron qobig‘ining elektr maydon ta’sirida deformatsiyalanadi. Natijada atoml ar (molekulalar) da musbat va manfi y zaryad markazlari ustma-ust tushmaydi. |
|
Dielektrik singdiruvchanlik |
|
|
Dielektrik ichida joylashtirilgan nuqtaviy zaryaddan r masofada turgan nuqtadagi maydon kuchlanganligi |
|
|
Qo‘zg‘almas Q musbat zaryaddan r masofada turgan +q zaryadning potensial energiyasi |
|
|
Nuqtaviy q zaryadning potensiali |
|
|
Elektr kuchlanish |
U = φ1 – φ2. |
|
Konservativ kuch |
Bajargan ishi zaryadning ko‘chish trayektoriyasiga bog‘liq bo‘lmagan kuch. |
|
Energiyaning hajmiy zichligi |
|

![]()
8-sinfda eletr toki mavjud bo‘lishi uchun 3 ta shart bajarilishi aytilgan edi.
1. Tok manbayi bo‘lishi.
2. Tok o‘tuvchi zanjirda erkin ko‘cha oladigan zaryadli zarralarning bo‘lishi.
3. Zanjir berk bo‘lishi.
Unda shuningdek qattiq, suyuqlik va gazlarda elektr toki o‘tishi qaralganda elektr qarshiligi tushunchasi kiritilgan edi. Elektr toki qanday zaryadli zarralar hisobiga mavjud bo‘ladi? Nima sababdan elektr tokining o‘tishiga muhit qarshilik ko‘rsatadi? Bunday savollarga javob berishdan oldin elektr o‘tkazuvchanlik tushunchasini kiritamiz.
![]() Elektr qarshiligiga
teskari bo‘lgan kattalikka elektr o‘tkazuvchanlik deyiladi.
Birligi nemis olimi E. R. Siemens sharafi ga qo‘yilgan.
Elektr qarshiligiga
teskari bo‘lgan kattalikka elektr o‘tkazuvchanlik deyiladi.
Birligi nemis olimi E. R. Siemens sharafi ga qo‘yilgan.
γ = R1 ; (8.1)
1 Siemens = 1S = 1 .
Ω
Metallarning elektr o‘tkazuvchanligini o‘rganishga XX asrning boshida kirishilgan edi. 1901-yilda nemis olimi Karl Rikke juda yaxshi silliqlangan uchta silindrdan (ikkita aluminiy va bitta mis) iborat zanjir tuzadi va undan bir yil davomida tok o‘tkazadi (8.1-rasm). Bu vaqt ichida silindrlardan umumiy miqdori 3,5 · 106 C zaryad o‘tadi, lekin bu silindrlar moddasining kimyoviy tarkibi o‘zgarishiga olib kelmadi. Tajriba tugab, silindrlar ajratilgach, ularning massalari ham o‘zgarmaganligi aniqlandi. Atomlarning bir-biriga o‘tish izlari qattiq jismlardagi oddiy diffuziya natijalaridan ortiq bo‘lmadi. Lekin, bu tajriba metallarda aynan qanday zarralar tufayli tok o‘tishini tushuntirib bermadi.
![]() Amerikalik fi ziklar T.
Styuart va R. Tolmenlar quyidagicha tajriba o‘tkazganlar. 1916-yilda
o‘tkazilgan bu tajribada – metall
o‘tkazgich o‘ralgan katta diametrli g‘altak olinib, uni 500 ayl/min chastota
bilan aylanma harakatga keltirilgan va birdaniga to‘xtatilgan (8.2-rasm). Bunda
g‘altakdagi erkin
Amerikalik fi ziklar T.
Styuart va R. Tolmenlar quyidagicha tajriba o‘tkazganlar. 1916-yilda
o‘tkazilgan bu tajribada – metall
o‘tkazgich o‘ralgan katta diametrli g‘altak olinib, uni 500 ayl/min chastota
bilan aylanma harakatga keltirilgan va birdaniga to‘xtatilgan (8.2-rasm). Bunda
g‘altakdagi erkin
|
zaryadlar yana biroz vaqt inersiya bilan harakatlanishda davom etganligi uchun qisqa vaqtli tok yuzaga kelgan. Buni |
8.1-rasm. |
![]() tok o‘tkazgich
uchlariga ulangan sirpanuvchi kontaktlar orqali ulangan galvanometr qayd etgan.
Olimlar tok tashuvchi zarral arning
tok o‘tkazgich
uchlariga ulangan sirpanuvchi kontaktlar orqali ulangan galvanometr qayd etgan.
Olimlar tok tashuvchi zarral arning ![]() solishtirma zaryadini tajribada
aniqlashdi. U 1,8 · 1011
C/ kg ga teng chiqib, elektronning solishtirma zaryadiga mos keladi.
solishtirma zaryadini tajribada
aniqlashdi. U 1,8 · 1011
C/ kg ga teng chiqib, elektronning solishtirma zaryadiga mos keladi.
Bu ilmiy fakt, metallar elektr o‘tkazuvchanligining klassik nazariyasiga asos bo‘ldi.
XX asr boshlarida nemis fi zigi P. Drude va golland fi zi gi
X. Lorens metallar elektr o‘tkazuvchanligining klassik nazar iyas ini 8.2-rasm. yaratishdi. Bu nazariyaning asosiy mazmuni quyidagilardan iborat:
1. Metallarda elektr o‘tkazuvchanlikning yuqori bo‘lishi, ularda birlik hajmga to‘g‘ri kelgan erkin elektronlarning ko‘pligidir. Masalan, misda erkin elektronlar konsentratsiyasi 8,4 · 1023 m–3 ga teng. Elektronlar xuddi gaz kabi panjara ionlari orasidagi fazoni to‘ldirib, tartibsiz va to‘xtovsiz harakatda bo‘ladi. Elektronlarning metallardagi tartibsiz harakat tezligi hisoblanganda taxminan 60–100 km/s ga teng chiqadi. Tashqi elektr maydon yo‘qligida, o‘tkazgichning istalgan kesim yuzasi orqali o‘tuvchi elektronlar harakati xaotik bo‘lganligidan elektr toki nolga teng bo‘ladi.
2*. P. Drude va X. Lorenslar o‘tkazuvchanlikning elektron nazariyasidan foydalanib zanjirning bir qismi uchun Om qonunini nazariy ravishda keltirib chiqarishdi.
|
o‘rt = Tok kuchi ta’rifi ga ko‘ra |
(8.2) |
|
I
= Bunda (8.1) hisobga olinsa, |
(8.3) |
|
I
= |
(8.4) |
Buning uchun uzunligi l, elektronlar
konsentratsiyasi n va ko‘ndalang kesim yuzi S bo‘lgan o‘kazgichni
qaraymiz (8.3-rasm). O‘tkazgich uchlariga U kuchlanish berilsa, hosil
bo‘lgan maydon kuchlanganligi E = ![]() ta’sirida elektronlar a
=
ta’sirida elektronlar a
= ![]() tezlanish oladi. t vaqtdan keyin
elektronning tezligi =
tezlanish oladi. t vaqtdan keyin
elektronning tezligi =![]() bo‘ladi. t – elektronlarning ikkita to‘qnashishlari oralig‘idagi vaqt.
To‘qnashishlarda elektron tezligi yo‘nalishi o‘zgaradi, lekin o‘rtacha tezlik
o‘zgarmaydi ga ega bo‘lamiz.
bo‘ladi. t – elektronlarning ikkita to‘qnashishlari oralig‘idagi vaqt.
To‘qnashishlarda elektron tezligi yo‘nalishi o‘zgaradi, lekin o‘rtacha tezlik
o‘zgarmaydi ga ega bo‘lamiz.
γ = 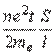 – ifoda
elektr o‘tka zuv chanlik deyiladi. γ =
– ifoda
elektr o‘tka zuv chanlik deyiladi. γ = ![]() o‘tkazuv chanlik
ekanligi hisobga olinsa, R =
o‘tkazuv chanlik
ekanligi hisobga olinsa, R =![]() – elektr qarshi
ligi ning ifodasi kelib chiqadi.
– elektr qarshi
ligi ning ifodasi kelib chiqadi.
![]() Bunda
Bunda ![]() = ρ– solishtirma qarshilik deyiladi.
Solishtirma qarshilik deyilganda uzunligi
= ρ– solishtirma qarshilik deyiladi.
Solishtirma qarshilik deyilganda uzunligi
8.3-rasm. 1 m, ko‘ndalang kesim yuzasi
1 m2 bo‘lgan o‘tkazgich qarshiligi
tushuniladi.
Shunday qilib
![]() Zanjirning bir
qismidan o‘tuvchi tok kuchi, o‘tkazgich uchlariga qo‘yilgan kuchlanishga va
o‘tkazuvchanlikka to‘g‘ri proporsional bo‘ladi.
Zanjirning bir
qismidan o‘tuvchi tok kuchi, o‘tkazgich uchlariga qo‘yilgan kuchlanishga va
o‘tkazuvchanlikka to‘g‘ri proporsional bo‘ladi.
I = γ · U. (8.5)
Mazkur bog‘lanishni XIX asr boshida tajriba yo‘li bilan nemis fi zigi G. Om topgan edi. Odatda, bunday bog‘lanish
I = ![]() (8.6)
ko‘rinishda ifodalanadi.
(8.6)
ko‘rinishda ifodalanadi.
![]() 8.4-rasmda o‘zgarmas temperaturada ikkita me tall
o‘tkazgichdan o‘tuvchi tok kuchining o‘tkazgich uchlariga qo‘yilgan
kuchlanishga bog‘liqligi keltirilgan.
8.4-rasmda o‘zgarmas temperaturada ikkita me tall
o‘tkazgichdan o‘tuvchi tok kuchining o‘tkazgich uchlariga qo‘yilgan
kuchlanishga bog‘liqligi keltirilgan.
O‘tkazgichlar, asboblar va iste’mol chilardan o‘tuvchi tok kuchining kuchlanishga bog‘liqlik grafi gi volt-amper xarakteristikasi deyiladi (VAX).
Moddalarning solishtirma elektr o‘tkazuvchanligi O I bo‘yicha olingan natijalar sanoat va xalq xo‘jaligida 8.4-rasm
ishlatiladigan elektrotexnik mahsulotlarni tayyorlashda
muhim ahamiyat kasb etadi. Tok o‘tkazuvchi kabel uchun, elektr tokini o‘tkazish qobiliyatiga ko‘ra, metall o‘tkazgichlar tanlanadi. Material noto‘g‘ri tanlansa, kuchlanish o‘zgarishi natijasida kabelning qizib ketishi hamda yong‘in chiqishiga sabab bo‘lishi mumkin.
Metallardan eng katta elektr o‘tkazuvchanlikka ega bo‘lgan material kumush hisoblanadi. Kumushning solishtirma elektr o‘tkazuvchanligi 20 0C da 63,3 MS/m ga teng. Kumushdan elektr simlarini tayyorlash qimmatga tushib ketishi tufayli elektr o‘tkazish qobiliyati jihatidan keyingi o‘rinda turadigan misdan foydalaniladi. Uning solishtirma elektr o‘tkazuvchanligi 58,14 MS/m ga teng. Mis o‘kazgichlar maishiy turmushda va ishlab chiqarishda keng qo‘llaniladi. Erish temperaturasi yuqori bo‘lganligidan u elektr yuklamalariga chidamli va qizigan holda uzoq muddat ishlay oladi.
Ishlatilishiga ko‘ra aluminiy o‘tkazgichlar misdan keyingi o‘rinda turadi. Uning solishtirma elektr o‘tkazuvchanligi 20°C da 35,71 MS/m ga teng. Uning erish temperaturasi misga nisbatan taxminan ikki barobar kam bo‘lib, yuklamalarga chidamliligi past.
Solishtirma elektr o‘tkazuvchanligi kichik bo‘lgan (nixrom 0,9 MS/m, fexral 0,77 MS/m) qotishmalardan elektr isituvchi asboblarning spirallari tayyorlanadi.
Elektrolitlarda solishtirma elektr o‘tkazuvchanlik temperaturaga, eritma konsentratsiyasiga, elektrolit tabiatiga bog‘liq. Elektrolit eritmalarning solishtirma elektr o‘tkazuvchanligi (metallardan farqli ravishda) temperatura ortishi bilan ortadi. Konsentratsiya ortishi bilan elektrolit eritmalarning solishtirma elektr o‘tkazuvchanligi dastlab ortadi, so‘ngra maksimal qiymatiga erishganidan so‘ng kamaya boshlaydi.
Solishtirma qarshilik yoki solishtirma elektr o‘tkazuvchanlikni o‘lchash uchun kondyktometr deb ataluvchi asboblar ishlatiladi. Kondyktometr yordamida suvning, kondensatning yoki bug‘ning sifati nazorat qilinadi. Qo‘llanilish sohasi – farmakologiya, meditsina, biokimyo, biofi zika, kimyoviy texnologiya, oziq-ovqat sanoati, suvni tozalash va h.k.
1.
![]() Metallarda qanday zarralarning tartibli harakati
tufayli elektr toki vujudga keladi?
Metallarda qanday zarralarning tartibli harakati
tufayli elektr toki vujudga keladi?
2. Sanoatda faqat elektr o‘tkazuvchanligi yuqori bo‘lgan materiallar ishlatiladimi?
3. Asbobning volt-amper xarakteristikasi deyilganda nima tushuni ladi?
![]()
Agar o‘tkazgichning ko‘ndalang kesim yuzasidan istalgan teng vaqtlar ichida teng miqdordagi zaryadlar oqib o‘tsa, o‘tkazgichdan o‘zgarmas tok o‘tmoqda deyiladi.
O‘tkazgichning ko‘ndalang kesim yuzasidan oqib o‘tgan zaryad miqdori (q) ning shu sarfl angan t vaqt oralig‘iga nisbati bilan o‘lchanadigan fi zik kattalikka tok kuchi deyiladi:
I
= ![]() . (8.7)
. (8.7)
Elektr tokining asosiy xarakteristikalaridan biri tok zichligi (j) hisoblanadi. Tok zichligi deb, tok kuchi I ning tok oqib o‘tayotgan yo‘nalishga perpendikulyar bo‘lgan ko‘ndalang kesim yuzasi S ga nisbati bilan o‘lchanadigan fi zik kattalikka aytiladi:
 (8.8)
(8.8)
Tok zichligi ![]() larda o‘lchanadi.
larda o‘lchanadi.
Tok kuchini
I = neo‘rtS
ko‘rinishda ifodalash mumkin. Bunda: n – zaryad tashuvchilar konsentratsiyasi; e – elektron zaryadi; o‘rt – zaryadli zarralar tartibli harakatining o‘rtacha tezligi; S – tok o‘tayotgan o‘tkazgichning ko‘ndalang kesim yuzasi.
U holda tok zichligini
![]() neo‘rtS j = = S = neo‘rt (8.9) ne –
ko‘paytma zaryad zichligini xarakterlaydi (birlik hajmdagi zaryad).
neo‘rtS j = = S = neo‘rt (8.9) ne –
ko‘paytma zaryad zichligini xarakterlaydi (birlik hajmdagi zaryad).
Shunga ko‘ra j = re o‘rt bo‘ladi.
Tok zichligi vektor kattalik bo‘lib, musbat zarra tezligi o‘rt yo‘nalishi bilan mos tushadi.
O‘tkazgichdagi tok zichligi, o‘tkazgich qanchalik darajada elektr energiyasi bilan yuklanganligini ko‘rsatadi. O‘tkazgichda ortiqcha isrofl arga yo‘l qo‘ymaslik hamda qimmatga tushmaslik uchun undagi tok zichligini optimal holda tanlash kerak bo‘ladi.
Tok zichligi kattaligiga o‘tkazgich materiali ta’sir etmasa-da, texnikada o‘tkazgichning solishtirma qarshiligi va uzunligiga qarab tanlanadi. Maishiy maqsadlarda ishlatiladigan o‘tkazgichlarni tokning tejamkor rejimiga moslab tanlanadi.
Xonadonlarda ishlatiladigan simlar uzun bo‘lmaganligidan, uning tejamkor tok zichligini 6 – 15 A/ mm2 oralig‘ida olinadi. Xonadondagi suvoq tagiga joylashtirilgan diametri 1,78 mm (2,5 mm2) bo‘lgan PVX izolyatsiyali mis o‘tkazgich 30, hatto 50 A tok kuchiga bardosh bera oladi.
Elektr uzatish liniyalarida tejamkor tok zichligi kichik bo‘lib, 1–3,4 A/mm2 atrofi da bo‘ladi. Sanoat chastotasi (50 Hz) da ishlaydigan elektr mashinalari va transformatorlarida bu qiymat 1 dan 10 A/mm2 gacha boradi.
Suyuqliklarda elektr toki o‘rganilganda elektrodlarda modda miqdori ajralib chiqqanligi bilan tanishsiz. Demak, ayrim muhitlardan elektr toki o‘tganida kimyoviy o‘zgarishlar ro‘y berar ekan. 8-sinfda, shuningdek, elektr toki o‘tganda o‘tkazgichlarning qizishini bilasiz. Demak, elektr tokining issiqlik ta’sirlari ham mavjud. Undan maishiy xizmat, sanoatda keng foydalaniladi.
O‘tkazgichlardan tok o‘tganda uning atrofi da magnit maydon bo‘lishini ilk bor daniyalik olim Xans Kristian Ersted 1820-yilda aniqlagan edi. Shundan so‘ng ko‘p o‘tmay fransuz olimi Andre Mari Amper tokli o‘tkazgichlarning o‘zaro ta’sirlashishini ochadi. Keyingi tadqiqotlar tokli o‘tkazgichlar magnit maydoni orqali ta’sirlashishini ko‘rsatdi. Tokning magnit ta’sirini o‘rganish elektrotexnikaning kuchli rivojlanishiga olib keldi. Ta’kidlash joizki, tok metallardan, elektrolitlardan, gazlardan va yarim o‘tkazgichlardan o‘tganda ham tokning magnit ta’siri mavjud bo‘ladi.
Metallardan tok o‘tganda uning kimyoviy ta’siri kuzatilmaydi.
Masala yechish namunasi
Diametri 1 mm bo‘lgan o‘tkazgichdan 5 A tok o‘tmoqda. O‘tkazgichdagi tok zichligini hisoblang.
![]()
![]()
![]() B e r i l g a n: F o r m u l a s i: Y
e c h i l i s h i:
B e r i l g a n: F o r m u l a s i: Y
e c h i l i s h i:
= 0,785 mm2.
= 6,37
.
![]() 1. Tok kuchi nima?
1. Tok kuchi nima?
2.Tok zichligining maishiy xizmatdagi va sanoatdagi ahamiyati nimada?
3.Elektr tokining ta’sirlarini tushuntirib bering.
![]()
37-mavzu. BUTUN ZANJIR UCHUN OM QONUNI.
TOK MANBAYINING FOYDALI ISH KOEFFITSIYENTI
O‘tkazgichdan tok o‘tganda u qiziydi va ma’lum miqdorda issiqlik ajralib chiqadi. Demak, energiyaning saqlanish qonuniga ko‘ra, o‘tkazgich bo‘ylab erkin elektronlar ko‘chganda elektrostatik maydon ish bajaradi. Lekin, elektr zanjirida energiya ajralsa, energiyaning saqlanish qonuniga ko‘ra, shuncha energiya elektr zanjiriga kelishi kerak. Shunday savol tug‘iladi: bu zanjirning qaysi qismida ro‘y beradi va qanday fi zik jarayonlar natijasida energiya elektr zanjiriga beriladi? Dastlab aniqlashtirib olamiz: elektr zanjiridagi energiya manbayi vazifasini elektrostatik maydon bajara oladimi?
Bajara olmaydi, chunki 33-mavzuda ko‘rib o‘tilganidek elektrostatik maydonda zaryadni berk trayektoriya bo‘ylab ko‘chirishda bajarilgan ish nolga teng. Demak, faqat elektrostatik maydon ta’sirida erkin zaryadlar berk zanjir bo‘ylab harakatlana olmaydi.
Aytilganlardan shu narsa kelib chiqadiki, zanjirning qandaydir bir qismida zaryadlarga elektrostatik bo‘lmagan kuchlar ta’sir qilishi kerak. Bu kuchlarni chet kuchlar deyiladi. Ular zaryadga tok mabayining ichida ta’sir qilib, aynan shu kuchlar energiyani elektr zanjiriga yetkazib beradi.
Tok manbayida chet kuchlar ta’sirida zaryadlarning ajralishi ro‘y beradi. Natijada manbaning bir qutbida musbat zaryad, ikkinchi qutbida manfi y zaryad to‘planadi. Qutblar orasida potensiallar farqi vujudga keladi.
Tokning kimyoviy manbalarida chet kuchlar kimyoviy tabiatga ega bo‘ladi. Masalan, agar rux va mis elektrodlarni sulfat kislotaga tushirilsa, ruxning musbat ionlari, misning musbat ionlariga nisbatan elektrodini tez-tez tashlab ketib turadi. Natijada mis va rux elektrodlar orasida potensiallar farqi vujudga keladi: mis elektrodning potensiali, ruxnikiga nisbatan katta bo‘ladi. Mis elektrod tok manbayining musbat qutbi, rux elektrod esa manfi y qutbi bo‘ladi.
Tok manbayida chet kuchlar erkin zaryadlarni elektrostatik maydon kuchlariga qarshi ko‘chirishda A chet ish bajaradi.
Bu ish berilgan vaqt ichida zanjir bo‘ylab ko‘chayotgan q zaryad miqdoriga proporsional bo‘ladi. Shunga ko‘ra chet kuchlarning bajargan ishining zaryad miqdoriga nisbati Achet ga ham, q ga ham bog‘liq bo‘lmaydi. Demak, u tok manbayining xarakteristikasi hisoblanadi. Bu nisbat, ya’ni birlik q musbat zaryadni berk zanjir bo‘ylab ko‘chirishda bajarilgan ishi manbaning elektr yurituvchi kuchi (EYuK) deyiladi va E harfi bilan belgilanadi:
Achet
![]() E = q . (8.9)
E = q . (8.9)
EYuK kuchlanish kabi voltlarda o‘lchanadi.
Agar zanjirdagi tok kuchi I bo‘lsa, t vaqt ichida zanjirdan q = It zaryad o‘tadi. Shunga ko‘ra (1) formulani quyidagicha yozib olamiz
Achet = E It. (8.10)
Bu paytda tok manbayining ichida va tashqi zanjirda
Qichki = I 2rt va Qtashqi = I 2Rt (8.11)
issiqlik miqdori ajralib chiqadi. Bunda r – manbaning qarshiligi bo‘lib, u ichki qarshilik deb ataladi.
Energiyaning saqlanish qonuniga ko‘ra
Qtashqi + Qichki = Achet. (8.12)
(8.9), (8.10) va (8.11) larni (8.12) ga qo‘yib, tegishli amallar bajarilganidan so‘ng
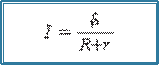 (8.13)
(8.13)
ga ega bo‘lamiz. Bu ifoda butun zanjir uchun Om qonuni deyiladi.
R + r ni zanjirning to‘la qarshiligi deyiladi.
Butun zanjir uchun Om qonunini
E = IR + Ir (8.14)
ko‘rinishda yozib olamiz. Bu ifodadagi birinchi qo‘shiluvchi, manba qutblaridagi U kuchlanishga teng:
IR = U.
Manba qutblaridagi maksimal kuchlanish E ga teng. Bu I = 0 bo‘lganda bo‘ladi. Tashqi zanjirga qarshilik ulanmasdan ochiq qolganda tok kuchi nol bo‘ladi. Ushbu holda
Umax = E.
Manba qutblarininig orasidagi minimal kuchlanish nolga teng. Bu hol qisqa tutashuv ro‘y berganda, ya’ni tashqi qarshilik R = 0 bo‘lganda kuzatiladi. Bu holda tok kuchi maksimal bo‘ladi:
 (8.15)
(8.15)
Uni qisqa tutashuv toki deyiladi.
Tashqi zanjirda bajarilgan ish foydali ish deyiladi. Uni Af bilan belgilaylik. Tokning bajargan ishi formulasidan foydalanib
Af = I 2Rt ni olamiz.
Achet = I 2Rt + I 2 rt bo‘lganligidan, foydali ishning chet kuchlar bajargan ishga nisbatini topamiz:
 . (8.16)
. (8.16)
Foizlarda ifodalangan bu nisbatni tok manbayining FIK deyiladi.
1.
![]() Nima sababdan elektrostatik maydon elektr zanjiridagi
energiya manbayi vazifasini bajara olmaydi?
Nima sababdan elektrostatik maydon elektr zanjiridagi
energiya manbayi vazifasini bajara olmaydi?
2. Chet kuchlar deyilganda nima tushuniladi?
3. Elektr yurituvchi kuch deyilganda nimaning kuchi nazarda tutiladi?
4. Qisqa tutashuv qanday hodisa?
![]()
Elektr tokining kimyoviy manbalarining qutblarida hosil bo‘ladigan EYuKning qiymati kichik bo‘ladi. Masalan, galvanik elementlar turkumiga kiruvchi Daniel elementining EYuK 1,11 V ga, Leklanshe elementiniki 1,4 V ga teng. Kislotali akkumulyatorining zaryadlagan zahoti o‘lchangan EYuK 2,7 V bo‘lsa, ishqorli akkumulyatorlarniki 1,3 V bo‘ladi.
Ko‘pgina texnik qurilmalarni ishlatish uchun katta kuchlanish talab qilinadi. Masalan, avtomobil motorini aylantirib ishga tushirib yuborish uchun katta quvvatli 12 V li o‘zgarmas tok manbayi kerak bo‘ladi. Bunday paytlarda elementlar yoki akkumulyatorlarni o‘zaro ketma-ket yoki parallel ulash kerak bo‘ladi.
Tok manbalarini o‘zaro ketma-ket yoki parallel ulashda hosil bo‘lgan zanjirlardagi tok kuchi va kuchlanishlarni hisoblashda Kirxgof qoidalaridan foydalaniladi.
Tok o‘tkazuvchi simlardan kamida uchtasi uchrashadigan nuqta tugun deyiladi. Tugunga kiruvchi tok yo‘nalishini musbat, chiquvchi tok yo‘nalishini manfi y deb qabul qilinadi (8.5-rasm).
![]() bc
bc
 a d
a d
fe
8.5-rasm. 8.6-rasm.
![]() Kirxgofning
birinchi qoidasi. Tugunga ulangan o‘tkazg ichlar orqali kiruvchi va undan
chiquvchi toklarning algebraik yig‘indisi nolga teng:
Kirxgofning
birinchi qoidasi. Tugunga ulangan o‘tkazg ichlar orqali kiruvchi va undan
chiquvchi toklarning algebraik yig‘indisi nolga teng:
I1 + I2 + I3 + ... + In = 0. (8.17)
Tarmoqlangan zanjirlarda har doim tok yo‘nalishi bo‘yicha bir qancha berk yo‘llarni ajratib olish mumkin. Bunday berk yo‘llar kontur deb ataladi. Ajratib olingan konturning turli qismlarida turlicha tok o‘tishi mumkin.
8.6-rasmda oddiy tarmoqlangan zanjir keltirilgan.
![]() Kirxgofning
ikkinchi qoidasi. Berk kontur tarmoqlaridagi kuchlanish tushuvlarining
algebraik yig‘indisi, konturdagi EYuKlarning algebraik yig‘indisiga teng:
Kirxgofning
ikkinchi qoidasi. Berk kontur tarmoqlaridagi kuchlanish tushuvlarining
algebraik yig‘indisi, konturdagi EYuKlarning algebraik yig‘indisiga teng:
I1R1 + I2R2 = – E1 – E2;
– I2R2 + I3R3 = E1 + E2; (8.18)
I1 + I2 + I3 = 0.
Tok manbalarini hisoblashda chet kuchlarning yo‘nalishi musbat hisoblanadi.
Mazkur qoidalardan foydalangan holda tok manbalarini ketma-ket va parallel ulab o‘rganamiz.
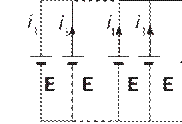
8.7-rasm. 8.8-rasm.
Masalani soddalashtirish uchun ulanuvchi barcha elementlarning EYuK lari E ni va ichki qarshiliklari r ni teng deb olamiz.
1. n ta elementni ketma-ket ulab batareya tuzaylik (8.7-rasm). Uni tashqi R qarshilikka ulaylik. Kirxgofning ikkinchi qonunini berk konturga tatbiq qilamiz: nE = I1R + nIr.
Bundan
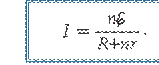 (8.19)
(8.19)
Demak, n ta elementni ketma-ket ulab, batareya tuzilganda umumiy EYuK n marta ortadi.
Bunday ulanish tashqi qarshilik, ichki qarshilikdan ko‘p marta katta bo‘lganida samarasi yuqori bo‘ladi. Darhaqiqat, R>>nr bo‘lganda, (8.19) formuladagi nr ni R ga nisbatan hisobga olmasa ham bo‘ladi. U holda
I
≈ ![]() ,
,
ya’ni n ta element ketma-ket ulanganda zanjirdagi tok kuchi, bitta elementga nisbatan n marta bo‘ladi.
2. Batareyani n ta elementni parallel ulab zanjir tuzaylik (8.8-rasm). Uni tashqi R qarshilikka ulaylik. Kirxgofning ikkala qonunini berk konturga tatbiq qilamiz.
I = nI1, E = IR + I1r
Bunda: I1 – bitta elementdan o‘tuvchi tok kuchi. Bundan,
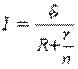 .
(8.20)
.
(8.20)
Demak, n ta elementni parallel ulab, batareya tuzilganda umumiy EYuK o‘zgarmaydi, ichki qarshiligi n marta kamayadi.
Parallel ulash tashqi qarshilik ichki qarshilikka nisbatan kichik bo‘lgan hollarda yaxshi samara beradi. R << r bo‘lganda (8.25) formulani
I ≈
n![]() ko‘rinishda yozib olamiz.
ko‘rinishda yozib olamiz.
Bundan umumiy tok kuchi, bitta element beradigan tok kuchiga nisbatan
n marta ortishi kelib chiqadi. b
Amaliyotda element EYuKlari va ichki qarshiliklari har xil bo‘lgan holatlar bo‘lishi mumkin.
![]() Dastlab, manbaning bir
xil ishoradagi E2, r2E1, r1
Dastlab, manbaning bir
xil ishoradagi E2, r2E1, r1
qutblari o‘zaro ulangan holni qaraylik. 8.9-rasmdagi elektr chizmada ichki qarshiliklari r1 va
r2 hamda EYuK lari E1 va E2 bo‘lgan ikkita I a
8.9-rasm.
elementning bir xil ishoradagi qutblari o‘zaro ulangan hol keltirilgan. Chizmaning a va b nuqtalariga ulangan voltmetr nimani ko‘rsatadi? Bunda voltmetrning ichki qarshiligi elementlarning ichki qarshiligidan ko‘p marta katta deb qaraladi.
Agar E2 > E1 bo‘lsa, zanjirdagi tok yo‘nalishi 8.9-rasmda ko‘rsatilganidek bo‘ladi. Voltmetrning ichki qarshiligi katta bo‘lganligidan undan o‘tuvchi tokni hisobga olmaymiz. Kirxgofning ikkinchi qoidasiga ko‘ra, elementrlarning ichki qarshiliklaridagi potensial tushuvlari elementlar EYuKlari yig‘indisiga teng.
Ir1 + Ir2 = E2 – E1. (8.21)
Bunda minus ishorasi olinishiga sabab, elementlar zanjirda qarama-qarshi yo‘nalishdagi toklarni hosil qiladi. Bundan zanjirdan otuvchi tok kuchi
|
Voltmetrning ko‘rsatishi |
(8.22) |
|
|
(8.23) |
Masala yechish namunasi
![]()
![]() Ichki qarshiliklari
0,4 Ω va 0,6 Ω bo‘lgan ikkita tok manbayidan birining EYuK 2 V,
ikkinchisiniki 1,5 V ga teng bo‘lib, 8.9-rasmda ko‘rsatilganidek ulangan. a
va b nuqtalar orasidagi kuchlanishni toping.
Ichki qarshiliklari
0,4 Ω va 0,6 Ω bo‘lgan ikkita tok manbayidan birining EYuK 2 V,
ikkinchisiniki 1,5 V ga teng bo‘lib, 8.9-rasmda ko‘rsatilganidek ulangan. a
va b nuqtalar orasidagi kuchlanishni toping.
![]() 1.
Kirxgof qoidalaridan qanday zanjirlarni hisobl ashda foydalan ish mumkin?
1.
Kirxgof qoidalaridan qanday zanjirlarni hisobl ashda foydalan ish mumkin?
2. Tok manbalarini ketma-ket ulash qanday hollarda foydali bo‘ladi?
3. Qanday hollarda tok manbalari parallel ulanadi?
![]()
Elektr zanjirlarida ishlatiladigan elektr o‘lchov asboblari ma’lum chegarada ishlay oladi. Masalan, galvanometr juda sezgir asbob bo‘lib juda kichik tok kuchi va kuchlanishni o‘lchay oladi. Ularning o‘lchash chegarasini oshirish uchun ularga qo‘shimcha ravishda qarshiliklar ulanadi.
![]()
 i
i
ir r
8.10-rasm. 8.11-rasm.
Galvanometrni ampermetr sifatida ishlatish uchun unga parallel ravishda shunt deb ataladigan, kattaligi juda kichik bo‘lgan qarshilik ulanadi (8.11rasm).
Galvanometr qarshiligini R, shunt qarshiligini r bilan belgilaylik. Galvanometr va shunt o‘zaro parallel ulanganligidan ularning uchlaridagi kuchlanish U ga teng bo‘ladi. U holda galvanometrdan va shuntdan o‘tuvchi tok kuchlari
Ig = ![]() va Ir =
va Ir = ![]()
ga teng bo‘ladi. Zanjirdagi umumiy tok kuchi I, galvanometrdan o‘tuvchi tok kuchi Ig dan n marta katta bo‘lsin:
I = n ·
Ig;
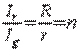
Zanjirdagi tok kuchi I = Ig + Ir = Ign + Ig = Ig (n + 1), yoki
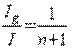 .
.
Shunday qilib, galvanometrdan o‘tuvchi tok kuchi, umumiy tok kuchidan (n + 1) marta kichik bo‘ladi. Tok kuchlari ifodalari orqali galvanometrga ulanadigan shunt qarshiligini topamiz:
![]() (n
– 1) =
(n
– 1) = ![]() ,
, 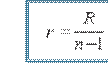 (8.24)
(8.24)
Shunday qilib galvanometrga parallel ravishda qarshiligi r bo‘lgan shunt ulansa, uning o‘lchash chegarasi n marta ortadi va asbob shkalasining bo‘linish darajasi (n + 1) marta ortadi.
Galvanometrni voltmetr sifatida ishlatish uchun unga ketma-ket ravishda qo‘shimcha qarshilik ulanadi (8.11-rasm). Bunda ham galvanometr qarshiligini R, qo‘shimcha qarshiligini r bilan belgilaylik. Galvanometr va qo‘shimcha qarshilik o‘zaro ketma-ket ulanganligidan ulardan o‘tuvchi tok kuchlari
I = Ig = Ir bo‘ladi. R va r ketma-ket ulanganligi sababli umumiy kuchlanish
U = I (R + r) = IR + I · r
bo‘ladi. Zanjirdagi umumiy kuchlanish U
ni Ug
ga nisbatini n = ![]() deb olamiz.
deb olamiz.
Bunda Ug – galvanometrning kuchlanishni o‘lchash
chegarasi. Umumiy kuchlanish ifodasini har ikkala tomonini Ug ga bo‘lib yuborsak, n
= 1 + ![]() bo‘ladi. Bundan
bo‘ladi. Bundan
![]() r
= R(n – 1). (8.25)
r
= R(n – 1). (8.25)
Demak, galvanometrga ketma-ket holda r qarshilik ulansa, uning kuchlanishni o‘lchash chegarasi n marta ortar ekan. Bu holda asbob shkalasining bo‘linish darajasi (n + 1) marta ortadi.
Odatda, katta qiymatli kuchlanishlarni o‘lchaydigan voltmetrlar shu tamoyilda ishlaydi.
Masala yechish namunasi
![]() 1. Qarshiligi 0,04 Ω bo‘lgan shunt ulangan ampermetr
tarmoqqa ulanganda 5 A ni ko‘rsatdi. Ampermetrning ichki qarshiligi 0,12 Ω.
Zanjirning tarmoqlanmagan qismidagi tok kuchini toping.
1. Qarshiligi 0,04 Ω bo‘lgan shunt ulangan ampermetr
tarmoqqa ulanganda 5 A ni ko‘rsatdi. Ampermetrning ichki qarshiligi 0,12 Ω.
Zanjirning tarmoqlanmagan qismidagi tok kuchini toping.
B e r i l g a n: F o r m u l a s i: Y e c h i l i s h i:
![]() r
= 0,04 Ω IA
= 5 A RA
= 0,12 Ω
r
= 0,04 Ω IA
= 5 A RA
= 0,12 Ω
Topish kerak
I = ?
r = , n = 0,12Ω+1 = 3 + 1 = 4;
0,04Ω
n = + 1I = 4 · 5 A = 20 A.
I = nIA
Javobi: 20 A.
1.
![]() Ampermetrga shunt qanday tanlanadi?
Ampermetrga shunt qanday tanlanadi?
2. Voltmetrga ulanadigan qo‘shimcha qarshilik qanday tanlanadi?
3. Voltmetrga qo‘shimcha qarshilikni parallel ulab qo‘yilsa nima bo‘ladi?
![]()
Ishning maqsadi: ampermetr va voltmetr yordamida tok manbayining elektr yurituvchi kuchini va ichki qarshiligini aniqlash.
Kerakli asboblar: 1) laboratoriya universal tok manbayi yoki akkumulyator batareyasi; 2) ampermetr; 3) voltmetr; 4) uzib-ulagich; 5) o‘tkazgich simlari; 6) 10 Ω,20 Ω li qarshiliklar.
![]() Ishning bajarilishi.
Ishning bajarilishi.
1. 8.12-rasmda keltirilgan elektr zanjiri yig‘i-
+ladi. Zanjirga 10 Ω li qarshilik ulanadi.
U2. Uzib-ulagich ochiq holda voltmetr ko‘r-
–satishi UV yozib olinadi. UV = E ga teng deb
olinadi.
8.12-rasm.
3. Uzib-ulagich ulanadi va ampermetr ko‘r-
satishi IA yozib olinadi.
4. Natijalari jadvalga ko‘chiriladi.
|
Tajriba № |
Uv, V |
U2, V |
IA, A |
E, V |
r, Ω |
|
1. |
|
|
|
|
|
|
2. |
|
|
|
|
|
5.
Tok manbayining ichki qarshiligi r = ![]() dan
hisoblanadi va natijasi jadvalga ko‘chiriladi.
dan
hisoblanadi va natijasi jadvalga ko‘chiriladi.
6. Zanjirga 20 Ω lik qarshilik ulanib tajriba takrorlanadi.
7. 1-tajriba va 2-tajribalarda topilgan r1 va r2 larni solishtiring.
![]() 1.
Elektr zanjirning qaysi qismini ichki, qaysi qismini tashqi zanjir deyiladi?
1.
Elektr zanjirning qaysi qismini ichki, qaysi qismini tashqi zanjir deyiladi?
2. Manbaning EYuK deganda nimani tushunamiz?
3. Manbaning ichki qarshiligi nima hisobiga hosil bo‘ladi?
8-mashq
1. Batareyaning EYuK 1,55 V. Uni qarshiligi 3 Ω bo‘lgan tashqi qarshilikka ulanganda batareya qisqichlaridagi kuchlanish 0,95 V ga teng bo‘ldi. Batareyaning ichki qarshiligi nimaga teng?
2. EYuK 30 V bo‘lgan batareya ulangan tok zanjiridagi tok kuchi 3 A ga teng. Batareya qisqichlaridagi kuchlanish 18 V. Batareyaning ichki qarshiligini va tashqi zanjir qarshiligini toping.
3. Elektr toki manbayini 5 Ω li qarshilikka ulanganda zanjirdagi tok kuchi 5 A ga, 2 Ω li qarshilikka ulanganda zanjirdagi tok kuchi 8 A ga teng bo‘ldi. Manbaning ichki qarshiligini va EYuK ni toping (Javobi: 3 Ω; 40 V).
4. Tok manbayi elementining EYuK 1,5 V. Qisqa tutashuv toki 30 A. Elementning ichki qarshiligi nimaga teng? Agar elementni qarshiligi 1 Ω bo‘lgan g‘altakka ulansa, element qutblaridagi kuchlanish qanchaga teng bo‘ladi?
5. Agar batareyaga ulangan tashqi qarshilik n marta ortganda, qarshilikdagi kuchlanish U1 dan U2 ga ortsa, batareyaning EYuK nimaga teng? (Javobi: E = U1 U2 (n–1)/ (U1n – U2)).
6. Qanday sharoitda batareya uchlaridagi kuchlanish uning EYuKdan katta bo‘lishi mumkin?
7. EYuK E1 va E2 bo‘lgan elementlar parallel ulangan. Agar ularning ichki qarshiliklari teng bo‘lsa, elementlar qisqichlaridagi potensiallar ayirmasini toping.
8. EYuK 1,5 V va 2 V bo‘lgan elementlar bir xil ishorali qutblari bilan ulangan. Batareya klemmalariga ulangan voltmetr 1,7 V kuchlanishni ko‘rsatdi. Elementlar ichki qarshiliklari nisbatini toping (Javobi: r1/r2 = 2/3).
9. EYuK 1,3 V va 2 V bo‘lgan elementlarning ichki qarshiliklari mos ravishda 0,1 Ω va 0,25 Ω ga teng. Ular parallel ulangan. Zanjirdagi tok kuchi va elementlar qisqichlaridagi kuchlanish topilsin.
10. Voltmetrning to‘rtta o‘lchash chegarasi bor: 3, 15, 75, 150 V.Asbobdan o‘tishi mumkin bo‘lgan tok kuchi 0,8 mA. Agar voltmetrning ichki qarshiligi 1000 Ω bo‘lsa, unga ulanadigan qo‘shimcha qarshiliklar R1, R2, R3 va R4 larni toping (Javobi: 9,49,249 va 499 kΩ).
11. Ichki qarshiligi 200 Ω bo‘lgan galvanometr tok kuchi 100 mkA bo‘lganda butun shkalasiga buriladi. Unga qanday qarshilikni ketma-ket qilib ulansa, voltmetr sifatida ishlab, 2 V kuchlanishgacha o‘lchay oladi?
1. Tok manbayining elektr yurituvchi kuchi qanday birlikda ifodalanadi?
A) N; B) J; C) A; D) V.
2. Manbaning EYuK 12 V. Manba ichida 50 C zaryadni bir qutbdan ikkinchisiga ko‘chirishda chet kuchlar necha joul ish bajaradi?
A) 60; B) 50; C) 330; D) 600.
3. Metallar elektr o‘tkazuvchanligining klassik nazariyasini kim birinchi bo‘lib yaratgaan?
A) P.Drude va golland fi zigi X.Lorens; B) E.R. Siemens;
C) K.Rikke; D) T.Styuart va R.Tolmen.
4. Ampermetrga ulanadigan shunt qanday tanlanadi va ulanadi?
RA– ampermetr qarshiligi, r – shunt qarshiligi.
A) RA>r, parallel ulanadi; B) RA>r, ketma-ket ulanadi; C) RA<r, ketma-ket ulanadi; D) RA<r, parallel ulanadi
5. Voltmetrga ulanadigan qo‘shimcha qarshilik qanday tanlanadi va ulanadi? Rv– voltmetr qarshiligi, r – qo‘shimcha qarshiligi.
A) Rv>r, parallel ulanadi B) Rv>r, ketma-ket ulanadi
C) Rv<r, ketma-ket ulanadi D) Rv<r, parallel ulanadi.
6. Elektr zanjiri qarshiligi 4 Ω bo‘lgan rezistordan va EYuK 12 V, ichki qarshiligi 2 Ω bo‘lgan tok manbayidan tuzilgan. Rezistordagi kuchlanish tushuvi necha volt?
A) 8; B) 2; C) 4; D) 12.
7. Gapni to‘ldiring. n ta elementni ... .. ulab, batareya tuzilganda umumiy EYuk n marta......
A) ... ketma-ket ... ortadi; B) ... ketma-ket ... kamayadi;
C) ... ketma-ket ... o‘zgarmaydi; D) ...parallel ... ortadi.
8. n ta elementni...... ulab batareya tuzilganda umumiy EYuK ..., ichki qarshiligi n marta...
A) ... parallel ... o‘zgarmaydi ... kamayadi;
B) ... parallel ... ortadi ... kamayadi;
C) ... parallel ... o‘zgarmaydi ... ortadi;
D) ... ketma-ket ... o‘zgarmaydi ... kamayadi.
9. Ichki qarshiligi 0,01 Ω bo‘lgan tok manbayi qisqa tutashganda, tok kuchi 1000 A bo‘ldi. Manba EYuKni toping (V).
A) 10; B) 9; C) 12; D) 15.
10. Ichki qarshiligi 2 Ω bo‘lgan batareyaga 50 Ω li tashqi qarshilik ulandi. Agar batareyaning EYuK 12 V bo‘lsa, FIK (%) ni toping.
A) 92; B) 89; C) 96; D)100.
|
Elektr toki mavjud bo‘lishi shartlari |
1. Tok manbayi bo‘lishi. 2. Tok o‘tuvchi zanjirda erkin ko‘cha oladigan zaryadli zarralarning bo‘lishi. 3. Zanjir berk bo‘lishi. |
|
Elektr o‘tkazuvchanlik |
Elektr qarshiligiga teskari bo‘lgan kattalik. |
|
Volt-amper xarakteristikasi (VAX) |
O‘tkazgichlar, asboblar va iste’molchilardan o‘tuvchi tok kuchining kuchlanishga bog‘liqlik grafi gi. O I |
|
Tok zichligi |
Tok kuchi (I) ning tok oqib o‘tayotgan
yo‘nalishga perpend ik ulyar bo‘lgan ko‘ndalang kesim yuzasi (S) ga
nisbati j = |
|
Elektr yurituvchi kuch (EYuK) |
A
|
|
Butun zanjir uchun Om qonuni |
|
|
Qisqa tutashuv toki |
|
|
Tok manbayining FIK |
|
|
Kirxgofning birinchi qoidasi |
Tugunga ulangan o‘tkazgichlar orqali kiruvchi va chiquvchi toklarning algebraik yig‘indisi nolga teng: I1 + I2 + I3 + ... + In = 0. |
|
Kirxgofning ikkinchi qoidasi |
Berk kontur tarmoqlaridagi kuchlanish tushuvlarining yig‘indisi, konturdagi EYuKlarning algebraik yig‘indisiga teng: I1R1 + I2R2 + ... + InRn = E1 + E2 + En. |
|
n ta elementni ketmaket ulab batareya tuzish |
tuzilganda umumiy EYuK n marta ortadi. |
|
n ta elementni parallel ulab batareya tuzish |
tuzilganda umumiy EYuK n marta kamayadi. |
|
Shunt |
Ampermetr o‘lchash chegarasini oshirish uchun asbobga parallel
ulanadigan kichik qiymatli qarshilik r = |
|
Qo‘shimcha qarshilik |
Voltmetr o‘lchash chegarasini oshirish uchun asbobga ketma-ket ulanadigan katta qiymatli qarshilik (shunt qarshilik), r = R(n–1) ga teng. |
![]()
Vakuumda elektr tokini o‘rganish uchun shisha yoki metall qalpoq (berk idish) ichiga bir-biridan ma’lum masofada ikkita elektrod o‘rnatiladi. Qalpoq ichidagi havo so‘rib olinadi. Havo shunday darajada so‘rilishi kerakki, molekulalar o‘z harakati davomida ikki elektrod orasida to‘qnashmasin. Buning uchun qalpoq ichida qolgan havo bosimi p << 10–13 mm sim. ust. atrofi da bo‘lishi kerak.
Elektrodlardan birini anod (A) deb ataymiz va uni manbaning musbat qutbiga ulaymiz. Ikkinchisini katod (K) deb ataymiz va uni manbaning manfi y qutbiga ulaymiz (9.1-rasm).
Anod va katod oralig‘iga kuchlanish qo‘yilganda zanjirga ulangan sezgir galvanometr hech qanday tok yo‘qligini ko‘rsatadi. Bu esa vakuumda tok tashuvchi zaryadli zarralar mavjud emasligini ko‘rsatadi.
![]() Zaryadli zarralarni
hosil qilish uchun katodni maxsus qizdirgich (Q) vositasida qizdiriladi.
Qizdirgich spiral shaklida yasalib undan alohida elektr toki o‘tkaziladi.
Zaryadli zarralarni
hosil qilish uchun katodni maxsus qizdirgich (Q) vositasida qizdiriladi.
Qizdirgich spiral shaklida yasalib undan alohida elektr toki o‘tkaziladi.
QMetallarning qizishi tufayli ulardan elektron 9.1-rasm. uchib chiqish hodisasiga termoe lektron emissiya deyiladi.
Katod qizdirilganda undan uchib chiqqan elektronlarga anod va katod oralig‘iga qo‘yilgan elektr maydoni ta’sir qiladi. Natijada elektronlar katoddan anod tomon tezlanish bilan harakatlanadi. Anod zanjiriga ulangan galvanometr tok mavjudligini qayd qiladi.
Endi anodni tok manbayining manfi y qutbiga, katodni esa musbat qutbga ulaylik. Bu holda galvanometr strelkasi burilmaydi, ya’ni zanjirdan tok o‘tmaydi.
![]() Vakuumda elektr
toki elektronlar oqimining tartibli harakatidan iborat.
Vakuumda elektr
toki elektronlar oqimining tartibli harakatidan iborat.
Anod va katoddan iborat vakuumli lampaga ikki elektrodli elektron lampa – diod deyiladi.
Istalgan elektron asbobning xossasi uning volt-amper xarakteristikasi, ya’ni undan o‘tuvchi tok kuchining asbobga qo‘yilgan kuchlanishga bog‘liqligi bilan belgilanadi.
Diodning volt-amper xarakteristikasini o‘rganish uchun diodning qizdirgichiga o‘zgarmas 4 V kuchlanish berilib, doimiy saqlanadi. Natijada qizdirgich bir xil ozgarmas T1 temperaturada qizib turadi. Anod va katod oralig‘idagi kuchlanish nolga teng bo‘lganda qizigan katoddan otilib chiqqan elektronlar katod atrofi da elektron bulutni hosil qiladi. Anod kuchlanishi orta borishi bilan elektron bulutdagi elektronlar anodga tomon harakatlana boshlaydi va elektron buluti tarqay boshlaydi. Bunda kuchlanish ortishi bilan anod toki ham orta boradi (9.2-rasm). Diodning volt-amper xarakteristikasida bu 1 sohaga to‘g‘ri keladi. Lekin keyinchalik kuchlanishning ortishi anod tokining ortishiga sezilarli ta’sir ko‘rsatmaydi va xarakteristikada bu 2 sohaga to‘g‘ri keladi. Bu paytda katoddan uchib chiqayotgan barcha elektronlar anodga yetib boradi va anod toki o‘zgarmay qoladi. Bu paytdagi anod tokiga to‘yinish toki deyiladi.
I
Qizdirgich kuchlanishini 6 V qilib tajriba n
I
takrorlansa, uning temperaturasi T2 bo‘ladi. n1
Bunda to‘yinish tokining qiymati ortadi. In3
Xarakteristikadan ko‘rinib turibdiki, tok kuchining kuchlanishga bog‘liqligi chiziqli
![]() emas.
Xarakteristikaning 1 qismida tok 0 kuchining kuchlanishga bog‘liqligi
emas.
Xarakteristikaning 1 qismida tok 0 kuchining kuchlanishga bog‘liqligi
Ia = kU 3/2
(9.1) qonuniyatga bo‘ysunishi aniqlangan. Bu formulani Boguslavskiy-Lengmyur formulasi deyiladi.
Katta quvvatga ega bo‘lgan yarim o‘tkazgichli diodlar ishlab chiqarilmasidan oldin vakuumli diodlardan o‘zgaruvchan toklarni to‘g‘rilashda foydalanilgan.
![]() 1. Vakuumda
elektr tokini kuzatish uchun elektron lampa ichidagi bosim qanchadan ko‘p
bo‘lmasligi kerak?
1. Vakuumda
elektr tokini kuzatish uchun elektron lampa ichidagi bosim qanchadan ko‘p
bo‘lmasligi kerak?
2. Vakuumda tok tashuvchi zarralar qanday hosil qilinadi?
3. Elektron bulut nima?
4. Dioddan qanday maqsadlarda foydalanish mumkin?
![]()
Metall o‘tkazgichlarning qarshiligi temperatura o‘zgarishiga qanday bog‘liq?
Buni mulohaza qilib ko‘raylik. Bir tomondan temperaturaning ortishi erkin elektronlar tezligining va to‘qnashishlar sonining ortishiga olib keladi. Bundan tashqari, kristall panjara tugunlaridagi ionlarning tebranish amplitudasi va uning harakatlanayotgan elektronlar bilan to‘qnashuvlari soni ortadi. Natijada zaryadlangan zarralarning tartibli harakat tezligi kamayadi, bu esa tok kuchining kamayishiga olib keladi.
Ikkinchi tomondan, temperatura ortganda birlik hajmdagi erkin elektronlar soni ortadi. Masalan, elektrolit eritmalarda ionlar soni ortadi.
Qaysi faktor ko‘proq rol o‘ynasa, temperaturaning ortishi o‘tkazgich qarshiligining ortishiga yoki kamayishiga olib kelishi mumkin.
Mazkur mulohazalarning to‘g‘riligini tekshirish uchun quyidagi tajriba o‘tkazilgan. Elektr lampochkasiga ketma-ket holda spiral shaklida bukilgan temir sim ulangan (9.3-rasm).
![]() Dastlab, lampochka ravshan yonib turadi. Spiral
qizdirilsa, lampochka ravshanligi kamayadi. Agar ularga ketma-ket ampermetr
ulansa, o‘tuvchi tok kuchining kamayganligini ko‘r sa tadi. Bu tajriba spiral
qizdiril ganda uning qarshiligi ortishini ko‘rsatadi. Shunday tajribani boshqa
metallar yoki metall qotishm alari bilan o‘tkazib ko‘rish mumkin.
Dastlab, lampochka ravshan yonib turadi. Spiral
qizdirilsa, lampochka ravshanligi kamayadi. Agar ularga ketma-ket ampermetr
ulansa, o‘tuvchi tok kuchining kamayganligini ko‘r sa tadi. Bu tajriba spiral
qizdiril ganda uning qarshiligi ortishini ko‘rsatadi. Shunday tajribani boshqa
metallar yoki metall qotishm alari bilan o‘tkazib ko‘rish mumkin.
Demak, metall o‘tkazgichlar qizdirilganda ularning qarshiligi ortar ekan.
9. 3-rasm.
Agar 0 °C da o‘tkazgich qarshiligi R0, t temperaturada R bo‘lsa, ular orasidagi bog‘lanish
R = R0(1 + αΔt) (9.2) bo‘ladi. Bunda: α – qarshilikning temperatura koeffi tsiyenti deyiladi. Uning fi zik ma’nosini anglab yetish uchun
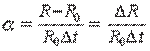 (9.3)
(9.3)
ni hosil qilamiz. Demak, α – koeffi tsiyent, temperatura 1 °C ga o‘zgarganda o‘tkazgich qashiligining o‘zgarishi 00C dagi qarshiligining qancha qismini tashkil etishini ko‘rsatadi. Aniq ishlaydigan elektron sxemalarda o‘tkazgich qarshiligining temperaturaga bog‘liqligini hisobga olish zarur bo‘ladi. Uni hisobga olmaslik qo‘shimcha xatoliklarning yuzaga kelishiga sababchi bo‘lishi mumkin.
O‘tkazgichlar qizdirilganda ularning geometrik o‘lchamlari kam o‘zgaradi. O‘tkazgichning qarshiligi asosan solishtirma qarshilikning o‘zgarishi bilan o‘zgaradi. Solishtirma qarshilikning temperaturaga bog‘liqligini topish uchun
(9.2)
ifodaga ![]() va lar qo‘yiladi.
va lar qo‘yiladi.
ρ = ρ0(1 + αΔt). (9.4)
Quyidagi jadvalda ba’zi bir metallar solishtirma qarshiligining tem peratura koeffi tsiyenti keltirilgan:
|
Metall yoki qotishma |
α, oC |
Metall yoki qotishma |
α, oC |
|
Aluminiy |
0,0042 |
Nikelin |
0,0001 |
|
Vismut |
0,0046 |
Nikel |
0,0065 |
|
Volfram |
0,0045 |
Niobiy |
0,003 |
|
Temir |
0,0062 |
Nixrom |
0,0002 |
|
Oltin |
0,0040 |
Qalay |
0,0044 |
|
Indiy |
0,0047 |
Platina |
0,0039 |
|
Kadmiy |
0,0042 |
Simob |
0,0010 |
|
Kobalt |
0,0060 |
Qo‘rg‘oshin |
0,0042 |
|
Mis |
0,0039 |
Kumush |
0,0040 |
|
Molibden |
0,0050 |
Xrom |
0,0059 |
|
Natriy |
0,0055 |
Xromal |
0,000065 |
|
Neyzilber |
0,0003 |
Rux |
0,0042 |
Metallarning solishtirma qarshiligining temperaturaga bog‘liqligidan qarshilikli termometrda foydalaniladi. Bunday termometrlar bilan juda yuqori va juda past temperaturalarni o‘lchash mumkin. Masalan, platinali termometrlar bilan –200 oC dan +600 oC gacha bo‘lgan temperaturalarni 0,0001 oC aniqlikda o‘lchash mumkin.
![]() Shunday qilib, metallarda temperatura pasayi shi bilan
qarshiligi kamayishi va absolyut nol temperaturada nolga teng bo‘lishi kerak.
Lekin ikkinchi tomondan qaralsa, absolyut nol temperaturada erkin
elektronlarning tezligi ham nolga intilishi natijasida o‘tkazgich qarshiligi
cheksiz katta bo‘lib ketishi kerak. Bu qarash larning qanchalik to‘g‘riligini
tajriba o‘tkazib tekshirish zarur edi. 1908-yilda golland fi zigi
KamerlingOnnes birinchi bo‘lib suyuq geliyni olishga erishdi. Aynan “geliy”
temperaturalarida ishlash Kamerling-Onnesga “o‘ta o‘tkazuvchanlik” hodisasini
ochishga imkon berdi. U oldin metallar so‘ngra simob bilan tajriba o‘tkazib
ko‘radi. Simob bilan o‘tkazilgan tajriba kutilmagan natijani beradi.
Temperatura pasayishi bilan simob qarshiligi pasayib boradi va 4,15 K (suyuq
geliyning qaynash temperaturasidan birmuncha past temperatura)da keskin kamayib
nolga tushib qoladi (9.4-rasm). 1911-yil 28-aprelda Kamerling-Onnes o‘z
natijalarini e’lon qiladi. Bu ixtironi u o‘ta o‘tkazuvchanlik deb
ataydi qiladi. Bu kutilmagan effekt bo‘lib, o‘sha davrdagi nazariyalar bilan
tushuntirib bo‘lmadi. 1912-yilda qo‘rg‘oshin va qalayda o‘ta o‘tkazuvchanlik
hodisasi kuzatiladi. Keyingi izlanishlarda bunday holat ko‘pgina metallar va
qotishmalarda 25 K dan past temperaturalarda kuzatiladi. 1957-yilda o‘ta
o‘tkazuvchanlik hodisasi Kuper va Bogolyubovlar tomonidan nazariy asoslandi.
1957-yilda Kollinz tomonidan o‘tkazilgan tajribada tok manbayi bo‘lmagan berk
zanjirda tok 2,5 yil mobaynida to‘xtovsiz oqib turgan. 1986-yilda
metallokeramika materiallarida yuqori temperaturali (100 K) o‘ta
o‘tkazuvchanlik jarayoni kuzatilgan.
Shunday qilib, metallarda temperatura pasayi shi bilan
qarshiligi kamayishi va absolyut nol temperaturada nolga teng bo‘lishi kerak.
Lekin ikkinchi tomondan qaralsa, absolyut nol temperaturada erkin
elektronlarning tezligi ham nolga intilishi natijasida o‘tkazgich qarshiligi
cheksiz katta bo‘lib ketishi kerak. Bu qarash larning qanchalik to‘g‘riligini
tajriba o‘tkazib tekshirish zarur edi. 1908-yilda golland fi zigi
KamerlingOnnes birinchi bo‘lib suyuq geliyni olishga erishdi. Aynan “geliy”
temperaturalarida ishlash Kamerling-Onnesga “o‘ta o‘tkazuvchanlik” hodisasini
ochishga imkon berdi. U oldin metallar so‘ngra simob bilan tajriba o‘tkazib
ko‘radi. Simob bilan o‘tkazilgan tajriba kutilmagan natijani beradi.
Temperatura pasayishi bilan simob qarshiligi pasayib boradi va 4,15 K (suyuq
geliyning qaynash temperaturasidan birmuncha past temperatura)da keskin kamayib
nolga tushib qoladi (9.4-rasm). 1911-yil 28-aprelda Kamerling-Onnes o‘z
natijalarini e’lon qiladi. Bu ixtironi u o‘ta o‘tkazuvchanlik deb
ataydi qiladi. Bu kutilmagan effekt bo‘lib, o‘sha davrdagi nazariyalar bilan
tushuntirib bo‘lmadi. 1912-yilda qo‘rg‘oshin va qalayda o‘ta o‘tkazuvchanlik
hodisasi kuzatiladi. Keyingi izlanishlarda bunday holat ko‘pgina metallar va
qotishmalarda 25 K dan past temperaturalarda kuzatiladi. 1957-yilda o‘ta
o‘tkazuvchanlik hodisasi Kuper va Bogolyubovlar tomonidan nazariy asoslandi.
1957-yilda Kollinz tomonidan o‘tkazilgan tajribada tok manbayi bo‘lmagan berk
zanjirda tok 2,5 yil mobaynida to‘xtovsiz oqib turgan. 1986-yilda
metallokeramika materiallarida yuqori temperaturali (100 K) o‘ta
o‘tkazuvchanlik jarayoni kuzatilgan.
Masala yechish namunasi
Elektr lampochkasidagi volframdan yasalgan spiralning 20 oC dagi qarshiligi 30 Ω ga teng. Lampochkani 220 V o‘zgarmas tok manbayiga ulanganda undan o‘tuvchi tok kuchi 0,6 A ga teng bo‘ldi. Lampaning yonishdagi spiral temperaturasini aniqlang.
![]()
![]() F o r m u l
a s i:
F o r m u l
a s i:
R = R0(1 + αΔt)
1.
![]() Metallarda temperatura ortishi bilan ularning
qarshiligi qanday o‘zgaradi?
Metallarda temperatura ortishi bilan ularning
qarshiligi qanday o‘zgaradi?
2. Metallar qarshiligining temperaturaga bog‘liq holda o‘zgarishidan qanday foydalaniladi?
3. O‘ta o‘tkazuvchanlik holatidan sanoat, transportda foydalanishning istiqbollari qanday?
![]()
Tabiatda shunday moddalar borki, ularning birlik hajmda elektronlar soni o‘tkazgichlarga nisbatan kam, lekin izolyator (dielektrik)larga nisbatan ko‘p. Shu sababli bunday moddalarni yarimo‘tkazgichlar deb ataldi.
Yarimo‘tkazgich moddalarda temperatura ortishi bilan ularning solishtirma qarshiligi kamayadi. Juda past temperaturalarda yarimo‘tkazgich modda dielektrik bo‘lib qoladi.
Metallarga yorug‘lik ta’sir etganda ularning elektr o‘tkazuvchanligi deyarli o‘zgarmaydi. Yarimo‘tkazgichga yorug‘lik tushirilganda ularning elektr o‘tkazuvchanligi ortadi.
Shunday qilib, yarimo‘tkazgichlarning asosiy farqli tomonlari quyidagilardan iborat:
a) elektr o‘tkazish qobiliyatiga ko‘ra metallar bilan dielektriklarning oraliq
holatini egallaydi;
b) isitilganda va yorug‘lik tushirilganda solishtirma qarshiligi kamayadi.
Yarimo‘tkazgich xususiyatiga ega bo‘lgan elementlarga germaniy, kremniy, tellur, selen va h.k.lar kiradi. Sizga kimyo fanidan ma’lumki, kimyoviy elementlar atom tuzilishi va xususiyatiga ko‘ra, D. I. Mendeleyevning davriy jadvalida yarimo‘tkazgich elementlar asosan III, IV va V guruhlarda joylashgan.
Yarimo‘tkazgichlarning tuzilishi. Xususiy o‘tkazuvchanlik
Yarimo‘tkazgichlarda elektr tokining tabiatini tushunish uchun, ularning tuzilishini bilish kerak. Buning uchun tarkibida hech qanday chet moddalar bo‘lmagan toza kremniy kristalini qaraylik. Siz 9-sinfda atom tuzilishi bilan tanishgansiz. Unda atomda elektronlar qobiq-qobiq bo‘lib joylashishini ham bilib olgansiz.
Kremniy atomida elektronlar qavatlar bo‘yicha joylashganda uning eng tashqi qobig‘ida to‘rtta elektroni joylashadi. Qo‘shni atomlar bir-birini shu elektronlar vositasida tutib turadi.
Har bir atom qo‘shni atom bilan o‘zining bitta elektroni orqali bog‘lanadi. Natijada ikkita atom o‘zaro ikkita elektron orqali bog‘lanadi. Bunday bog‘lanishni kovalent bog‘lanish deyiladi.
Kovalent bog‘lanishda qatnashayotgan elektronlarni valent elektronlar deb ham yuritiladi. Demak, valent elektronlar butun kristall atomlariga tegishli bo‘ladi.
Elektron o‘tkazuvchanlik. Past temperaturalarda juft elektronlar hosil qilgan bog‘lanish kuchli bo‘lib, uzilmaydi.
Shu sababli past temperaturalarda kremniy elektr tokini o‘tkazmaydi. Temperatura ko‘tarilganda valent elektronlarning kinetik energiyasi ortadi. Ayrim bog‘lanishlar uzila boshlaydi. Ulardan ayrimlari borib-kelib, yurgan yo‘lidan chiqib, metalldagi kabi erkin elektronga aylanadi. Mazkur elektronlar elektr maydoni ta’sirida yarimo‘tkazgich bo‘ylab ko‘chadi va elektr tokini hosil qiladi (9.5-rasm).
Erkin elektronlarning ko‘chishi tufayli yarimo‘tkazgichda tok hosil bo‘lishiga elektron o‘tkazuvchanlik yoki qisqacha n-turdagi o‘tkazuvchanlik (lotin. negativus – manfi y) deyiladi.
Kovakli o‘tkazuvchanlik. Kovalent bog‘lanishda qatnashgan elektron chiqib ketgan joyda kovak hosil bo‘ladi. Neytral atomdan manfi y zaryadli elektron chiqib ketgan joy musbat zaryadga ega bo‘ladi.
9.5-rasm.
Bo‘sh kovakni kovalent bog‘lanishdagi boshqa elektron kelib berkitadi. Lekin endi kovak boshqa joyda paydo bo‘ladi. Shunday qilib, elektronning bir joydan ikkinchi joyga ko‘chishida, kovaklarning ham nisbatan ko‘chishi ro‘y beradi.
Elektr maydoni bo‘lmaganda elektronlarning va shunga mos kovaklarning ko‘chishi tartibsiz bo‘ladi.
Elektr maydoni qo‘yilganda erkin elektronlar bir tomonga, kovaklar ikkinchi tomonga ko‘chadi.
Xuddi shunday yarim o‘tkazich boshida hosil bo‘lgan kovakka qo‘shni atomdan elektronning sakrab o‘tishida musbat zaryadli kovak o‘tkazgichning oxiri tomon siljiydi (9.6-rasm).
Bunday o‘tkazuvchanlikni yarimo‘tkazgichlarning kovakli o‘tkazuvchanligi yoki qisqacha p-turdagi o‘tkazuvchanlik (lotin. positivus – musbat) deyiladi.
9.6-rasm.
Shunday qilib, sof (hech qanday aralashmalarsiz) yarimo‘tkazgichlarda erkin elektronlarning harakati bilan bog‘liq elektron o‘tkazuvchanlik, kovaklar harakati bilan bog‘liq kovakli o‘tkazuvchanlik bo‘ladi.
Aralashmalarsiz, sof yarimo‘tkazgichdagi o‘tkazuvchanlikni xususiy o‘tkazuvchanlik deyiladi. Bunda mazkur moddadagi elektron va kovakli o‘tkazuvchanlik deyarli teng bo‘ladi.
Sof yarimo‘tkazgichlarda erkin elektronlar va kovaklar soni kam bo‘lganligidan elektr o‘tkazish qobiliyati kichik bo‘ladi.
Aralashmali yarimo‘tkazgichlar: donorli aralashmalar. Endi sof yarimo‘tkazgichli kremniyga ozgina aralashma kiritaylik. Dastlab kremniy atomlari orasiga besh valentli mishyak (As) kiritaylik.
Bunda kremniyning to‘rtta kovalent bog‘lanish hosil qiluvchi elektroni o‘rnini mishyakning to‘rtta elektroni egallaydi. Mishyakning beshinchi elektroni bo‘sh qolib, erkin elektronga aylanadi (9.7 a-rasm).
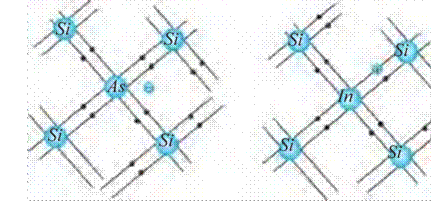
a) b)
9.7-rasm.
Natijada erkin elektronlar soni kovaklar sonidan ortiq bo‘ladi. Yarimo‘tkazgichning solishtirma qarshiligi keskin kamayadi. Bunda qo‘shilgan mishyak atomlarining soni yarimo‘tkazgich atomlari sonining o‘n milliondan bir qismini tashkil etganda, erkin elektronlarning konsentratsiyasi (1 sm3 ga to‘g‘ri kelgan elektronlar soni) sof yarimo‘tkazgichnikiga nisbatan ming barobar katta bo‘ladi. Qo‘shilganda osongina elektronini beradigan aralashmalarni donorli aralashmalar deyiladi. Donorli aralashmalarda asosiy tok tashuvchi zarralar elektronlar bo‘lganligi uchun, ularni n-turdagi yarimo‘tkazgichlar deyiladi. Kovaklar bunday yarimo‘tkazgichlarda asosiy bo‘lmagan zaryad tashuvchilarga kiradi.
Akseptorli aralashmalar. Sof yarimo‘tkazgichli kremniyga indiy moddasini aralashtiraylik. Indiy (In) uch valentli bo‘lganligidan, uning uchta elektroni kremniy atomi bilan kovalent bog‘lanish hosil qiladi. Bunda indiyning qo‘shni atomlar bilan normal holdagi juft elektronli kovalent bog‘lanish hosil qilishi uchun bitta elektron yetmaydi. Natijada kovak hosil bo‘ladi. Kristallga qancha indiy atomi kiritilsa, shuncha kovak hosil bo‘ladi (9.7 b-rasm).
Bunday turdagi aralashmani akseptorli aralashmalar deyiladi. Yarimo‘tkazgich elektr maydoniga kiritilganda, kovaklar ko‘chishi ro‘y berib, kovakli o‘tkazuvchanlik hosil bo‘ladi. Asosiy tok tashuvchilari kovaklardan iborat bo‘lgan aralashmali yarimo‘tkazgichlarni p-turdagi yarimo‘tkazgichlar deyiladi. Bunday yarimo‘tkazgichlarda elektronlar asosiy bo‘lmagan zaryad tashuvchilar hisoblanadi.
![]() 1.
Qanday xususiyatiga ko‘ra ularni yarimo‘tkazgichlar deb nomlashgan?
1.
Qanday xususiyatiga ko‘ra ularni yarimo‘tkazgichlar deb nomlashgan?
2. Elektron o‘tkazuvchanlik qanday zarralarning harakati bilan bog‘langan?
3. Elektron bilan kovak uchrashganda qanday hodisa ro‘y beradi?
4. Nima sababdan yarimo‘tkazgichning qarshiligi unga kiritilgan aralashmaga kuchli darajada bog‘liq?
5. Akseptor aralashmali yarimo‘tkazgichda qanday zaryad tashuvchilar asosiy hisoblanadi?
![]() D.I. Mendeleyevning
kimyoviy elementlar davriy sistemasi jadvalini oling. Undan III va V guruhdan
aralashma sifatida ishlatsa bo‘ladigan elementlarni yozib oling. IV guruhdagi
yarimo‘tkazgich bilan aralashmali yarimo‘tkazgich hosil bo‘lish chizmasini
chizing.
D.I. Mendeleyevning
kimyoviy elementlar davriy sistemasi jadvalini oling. Undan III va V guruhdan
aralashma sifatida ishlatsa bo‘ladigan elementlarni yozib oling. IV guruhdagi
yarimo‘tkazgich bilan aralashmali yarimo‘tkazgich hosil bo‘lish chizmasini
chizing.
![]()
44-mavzu. YARIMO‘TKAZGICHLI ASBOBLAR (DIOD, TRANZISTOR) VA ULARNING
|
ktronlar tezgina bo‘sh kovaklarni to‘ldiradi. Natijada yarimo‘tkazgichning o‘rta qismida zaryad tashuvchilar bo‘lmagan soha hosil bo‘ladi. Bu sohaning xususiyati dielektriknikiday bo‘ladi. |
berkituvchi
qatlam 9.8-rasm. |
![]() Biror yarimo‘tkazgich kristalining bir tomonida n-turdagi,
ikkinchi tomonida p-turdagi yarimo‘tkazgichni hosil qilaylik (9.8-rasm).
Yarimo‘tkazgichning o‘rta qismida erkin eleShunga ko‘ra bu soha bundan keyin
elektronlarning p-sohaga, kovaklarning n-sohaga o‘tishiga
to‘sqinlik qiladi. Shu sababli uni berkituvchi qatlam deyiladi.
Biror yarimo‘tkazgich kristalining bir tomonida n-turdagi,
ikkinchi tomonida p-turdagi yarimo‘tkazgichni hosil qilaylik (9.8-rasm).
Yarimo‘tkazgichning o‘rta qismida erkin eleShunga ko‘ra bu soha bundan keyin
elektronlarning p-sohaga, kovaklarning n-sohaga o‘tishiga
to‘sqinlik qiladi. Shu sababli uni berkituvchi qatlam deyiladi.
Mazkur yarimo‘tkazgichni tok manbayiga ulaylik. Dastlab yarim o‘tkazgichning p-sohasini manbaning manfi y qutbiga, n-sohasini manbaning musbat qutbiga ulaylik (9.9-rasm).
Bunda elektronlar manbaning musbat qutbiga, kovaklar manbaning manfi y qutbiga tortiladi. Natijada berkituvchi qatlam kengayadi. Yarimo‘tkazgich orqali deyarli tok o‘tmaydi. Bunday holat teskari p–n o‘tish deb ataladi.
Endi yarimo‘tkazgichning p-sohasiga manbaning musbat qutbini, n-sohasiga manbaning manfi y qutbini ulaylik. Bunda elektronlar n-sohadan itarilib p-sohaga tortiladi.
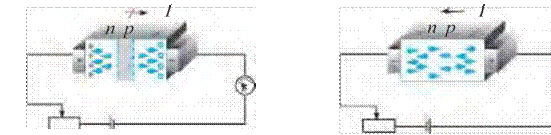
9.9-rasm 9.10-rasm
Kovaklar esa p-sohadan itarilib, n-sohaga tortiladi. Natijada berkituvchi qatlam torayadi va undan zaryad tashuvchilar o‘ta boshlaydi (9.9-rasm). Yarimo‘tkazgichdan tok o‘tadi. Bunday holatni to‘g‘ri p–n o‘tish deyiladi. To‘g‘ri p–n o‘tishda yarimo‘tkazgichning elektr qarshiligi, teskari p–n o‘tishga nisbatan bir necha marta kichik bo‘ladi. Yarimo‘tkazgichda p–n o‘tish tufayli tok faqat bir yo‘nalishda o‘tadi. Uning bu xususiyatidan yarimo‘tkazgichli asboblarda foydalaniladi.
Yarimo‘tkazgichli diod
Yarimo‘tkazgichlarda p–n o‘tishni hosil qilish uchun p va n o‘tkazuvchanlikka ega bo‘lgan ikkita yarimo‘tkazgichni mexanik ravishda ulash yetarli bo‘lmaydi. Chunki bu holda ulardagi oraliq katta bo‘ladi. p va n o‘tishdagi qalinlik atomlararo masofaga teng bo‘ladigan darajada kichik bo‘lishi kerak. Shu sababli donor aralashmaga ega bo‘lgan germaniy monokristali yuzalaridan biriga indiy kavsharlanadi. Diffuziya hodisasi tufayli indiy atomlari germaniy monokristali ichiga kiradi. Natijada germaniy yuzasida p-turdagi o‘tkazuvchanlikka ega bo‘lgan soha hosil bo‘ladi.
Germaniy monokristalining indiy atomlari kirmagan sohasi avvalgidek n-turdagi o‘tkazuvchanlikka ega bo‘ladi. Oraliq sohada p–n o‘tish hosil bo‘ladi (9.11 a-rasm).
Bitta p–n o‘tishga ega bo‘lgan yarimo‘tkazgichli asbobga yarimo‘tkazgichli diod deyiladi.
Yarimo‘tkazgichli diodga yorug‘lik, havo va tashqi elektr, magnit maydonlarining ta’sirlarini kamaytirish uchun germaniy kristali germetik berk metall qobiqqa joylashtiriladi.
![]() Yarimo‘tkazgichli diodning shartli belgisi 9.11 b-rasmda
keltirilgan.
Yarimo‘tkazgichli diodning shartli belgisi 9.11 b-rasmda
keltirilgan.
Tranzistor haqida tushuncha.
Ikkita p–n o‘tishga ega bo‘lgan yarimo‘tk azgichli sistemaga tranzistor deyi ladi. Tranzistor yordamida elektr tebranish lari hosil qilinadi, boshqariladi va kuchaytiriladi.
Tranzistorni tayyorlash uchun elektron o‘tkazuvchanlikka ega bo‘lgan germaniy kristalining ikkita tomoniga indiy kavsharlanadi. Germaniy kristalining qalinligi juda kichik bo‘ladi (bir necha mikrometr). Mana shu qatlam tranzistor asosi, ya’ni bazasi deb ataladi (9.12 a-rasm).
![]()
 p n p
p n p
9.13-rasm.
Uning kovakli o‘tkazuvchanlikka ega bo‘lgan ikkita tomonidan сhiqarilgan uchlari emitter va kollektor deyiladi. Bunday turdagi tranzistorni p–n–p strukturali tranzistor deyiladi (9.12 a-rasm).
9.12-rasm. Tranzistorning emitter sohasidagi kovaklar konsentratsiyasi, bazadagi elektronlar konsent rat siyasiga nisbatan bir necha marta katta qilib tayyorlanadi. Tranzistorning shartli belgisi 9.12 b-rasmda keltirilgan. Tranzistorning ishlashini qaraylik (9.13-rasm).
Emitter – baza oralig‘iga ulangan B1 batareya kuchlanishi to‘g‘ri p–n o‘tishni hosil qiladi. Kollektor – baza oralig‘idagi B2 batareya teskari p–n o‘tishni hosil qiladi. Unda kollektorda tok qanday hosil bo‘ladi? Baza – emitter oralig‘iga qo‘yilgan kuchlanish ta’sirida kovaklar bazaga kirib keladi. Bazaning qalinligi juda kichik bo‘lganligi hamda unda elektronlar konsentratsiyasi kam bo‘lganligidan kovaklarning juda kam qismi elektronlarga birikadi. Ko‘pchilik kovaklar esa kollektor sohasiga o‘tib qoladi.
Kollektorga B2ning manfi y qutbi ulanganligidan kovaklar unga tortilib, kollektor tokini tashkil etadi. Emitter – baza zanjiridagi tok kuchi, emitter – kollektor yo‘nalishidagi tok kuchidan ancha kichik bo‘ladi. Emitter – baza yo‘nalishidagi tok kuchi o‘zgarsa, emitter – kollektor yo‘nalishida o‘tayotgan tok kuchi ham o‘zgaradi. Shunga ko‘ra tranzistordan o‘zgaruvchan tok signallarini kuchaytirishda foydalaniladi.
Tranzistorni tayyorlashda baza sifatida p-turdagi yarimo‘tkazgich olinishi ham mumkin. Bu holda emitter va kollektor sohasi n-turdagi yarimo‘tkazgichdan tayyorlanadi. Bunday tranzistorni n–p–n strukturali tranzistor deyiladi.
Bunday turdagi tranzistorlarning ishlash prinsipi p–n–p turdagi tranzistordan farq qilmaydi. Bu tranzistorda faqat tok yo‘nalishi kollektordan emitterga tomon bo‘ladi.
Integral mikrosxemalar*
O‘tgan asrning 70-yillarida o‘n so‘mlik tangadek keladigan yarimo‘tkazgich material bo‘lagida minglab mikroskopik tranzistorlar joylashtirilgan mikrosxemalar kashf qilindi. Ularda tranzistorlar bilan birgalikda diodlar, kondensatorlar, rezistorlar va boshqa radioelektron elementlar ham joylashtirilganligidan integral mikrosxema deb ataldi. Bu kashfi yot kichik bir hajmda murakkab sxemalarni joylashtirish va stol kompyuterlarini yaratish imkoniyatini tug‘dirdi. Dastlabki davrda radioelementlar yarimo‘tkazgich yuzasida yasalgan bo‘lsa, keyinchalik ularni butun hajmda hosil qilina boshlandi. Ularni mikrochiplar deb atala boshlandi. Mikrochiplar asosida qo‘l telefonlari, ko‘tarib yuriladigan kompyuter (Noutbuk) va h.k. mitti radioelektron qurilmalar yasalmoqda. Hozirgi kunda tangadek keladigan mikrochipda yuz millionlab tranzistor va radioelementlar joylashtirilmoqda. Bu degan so‘z, radioelement o‘lchami ≈10–9 m atrofi da deganidir. 10–9 m bir nanometrga teng. Shunga ko‘ra bunday mikrosxemalarni loyihalash, yasash ishlari bilan shug‘ullanadigan soha nanotexnologiya deviladi.
Bu sohani o‘rganish va ularni takomillashtirishni, avvalo, eng sodda elektrotexnik qurilmalarni yasash va ishlashini o‘rganishdan boshlanadi.
O‘zgaruvchan tokni o‘zgarmas tokka aylantirib beruvchi to‘g‘rilagich. Ma’lumki televizor, radiopriyomnik va shu kabi asboblarni kundalik turmushda o‘zgaruvchan 220 V tarmog‘iga ulab ishlatamiz. Lekin uni tashkil etgan diod, tranzistor kabi yarimo‘tkazgichli asboblar esa o‘zgarmas tok manbayiga ulanishi kerak. Demak, mazkur asboblarda o‘zgaruvchan tokni o‘zgarmas tokka aylantirib beruvchi alohida qismi bo‘lishi kerak. 9.14-rasmda mana shunday qurilmaning sodda sxemasi keltirilgan.
 U U
U U
a) b) d)
9.14-rasm.
Bu sxemada transformator birlamchi chulg‘amiga o‘zgaruvchan 220 V kuchlanish berilganda, ikkilamchi chulg‘amidan 12 V olinadi. Yarimo‘tkazgichli diod kuchlanishning musbat yarim davrida tokni o‘tkazadi. Manfi y yarim davrida esa o‘tkazmaydi. Shunga ko‘ra bu sxemadagi qurilma bitta yarim davrli to‘g‘rilagich deyiladi.
To‘g‘rilagich kirishi va sxemadagi kuchlanish shakllari 9.14 b-rasmda keltirilgan. Rasmdan ko‘rinib turibdiki, sxemada kuchlanishning faqat yarmidan foydalaniladi. Bundan tashqari, uning kattaligi ham kuchli o‘zgaradi. Shu sababli ikki yarim davrli to‘g‘rilagich ishlatiladi.
![]() 1.
Yarimo‘tkazgichli diod nima sababdan tokni faqat bir lomonga o‘tkazadi?
1.
Yarimo‘tkazgichli diod nima sababdan tokni faqat bir lomonga o‘tkazadi?
2. p–n o‘tish nima?
3. Yarimo‘tkazgich qarshiligi p–n o‘tishga qanday bog‘liq?
4. Tranzistorda to‘g‘ri va teskari p–n o‘tishlar uning qaysi sohalarida bo‘ladi?
5. p–n–p va n p–n turdagi tranzistorlar nimasi bilan farqlanadi?
![]()
45-mavzu. LABORATORIYA ISHI: YARIM OTKAZGICHLI DIODNING VOLT – AMPER XARAKTERISTIKASINI
Ishning maqsadi. Yarim otkazgichli dioddan o‘tuvchi tok kuchining qo‘yilgan kuchlanishga bog‘liqligini o‘rganish.
Kerakli asboblar: 1) yarimo‘tkazgichli diod (kolodkada); 2) o‘zgarmas tok manbayi (36–42 V); 3) uzib-ulagich; 4) o‘tkazgich simlari; 5) milliampermetr; 6) reostat; 7) voltmetr.
Ishning bajarilishi:
1.
![]() Kerakli asboblar to‘planib, 9.15-rasmdagi chizma bo‘yicha
elektr zanjiri yig‘iladi.
Kerakli asboblar to‘planib, 9.15-rasmdagi chizma bo‘yicha
elektr zanjiri yig‘iladi.
2. Reostat jildirgichini surib chiqishda 0 V bo‘ladigan holatga qo‘yiladi.
3. Uzib-ulagich ulanadi.
4. Reostat jildirgichini surib, tashqi zanjirga
beriladigan kuchlanish orttirib boriladi. Voltmetr va ampermetr ko‘rsatishlari yozib boriladi.
5. O‘lchash natijalari jadvalga kiritiladi.
|
U, V |
|
|
|
|
|
|
|
|
I, A |
|
|
|
|
|
|
|
6. Tok manbayining qutblari almashinib ulanadi va tajriba takrorlanadi.
7. Natijalariga ko‘ra yarim otkazgichli dioddan o‘tuvchi tok kuchining qo‘yilgan kuchlanishga bog‘liqlik grafi gi chiziladi.
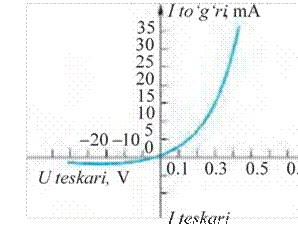 U to‘g‘ri, V
U to‘g‘ri, V
9.16-rasm.
8. Yarim o‘tkazgichli dioddan to‘g‘ri p–n o‘tish va teskari p–n o‘tish yo‘nalishda o‘tadigan tok kuchining qo‘yilgan kuchlanishga bog‘liqligi 9.16-rasmdagi grafi kda keltirilgan.
Diodga teskari yo‘nalishdagi kuchlanish qo‘yilganda diodning pasportida yozilgan qiymatidan katta kuchlanishni qo‘yish mumkin emas.
1.
Diod to‘g‘ri ulangan holda tok kuchining qo‘yilgan
kuchlanishga ![]() bog‘liqligi to‘g‘ri chiziqdan iborat
emasligiga e’tibor bering va sababini tushuntirishga harakat qiling.
bog‘liqligi to‘g‘ri chiziqdan iborat
emasligiga e’tibor bering va sababini tushuntirishga harakat qiling.
2. Nima sababdan teskari yo‘nalishda kuchlanish qo‘yilsa, undan tok o‘tadi?
3. Olingan ma’lumotlardan foydalanib diodning to‘g‘ri va teskari o‘tish yo‘nalishlari uchun elektr qarshiliklarini hisoblang.
9-mashq
1. Mis sterjendan 0,5 s davomida zichligi 9 A/mm2 bo‘lgan tok o‘tganda uning temperaturasi qanday o‘zgaradi? Misning solishtirma qarshiligi 1,7 · 10–8 Ω · m, zichligi 8900 kg/m3, solishtirma issiqlik sig‘imi 380 J/(kg K) (Javobi: 0,20 oC).
2. Niobiydan yasalgan spiral 100 oC ga qizdirilsa uning solishtirma qarshiligi necha marta o‘zgaradi? Niobiy uchun α = 0,003 K–1 (Javobi: 1,3 marta ortadi).
3. Nikelin simning 20 oC dagi qarshiligi 20 Ω ga teng edi. Uni 120 oC gacha qizdirilsa, qarshiligi nimaga teng bo‘ladi? Nikelin uchun α = 0,0001 K–1.
4. Vakuumli diodda elektron anodga 8 Mm/s tezlik bilan yetib boradi. Anod kuchlanishini toping (Javobi: 180 V).
5. Vakuumli diodda anoddagi maksimal tok kuchi 50 mA ga teng bo‘ldi. Katoddan har sekundda nechta elektron uchib chiqmoqda? (Javobi:
3,1 · 1017).
6. Yarimo‘tkazgichlarda musbat ion bilan kovak orasida farq bormi?
7. Nima sababdan tashqi sharoitlar o‘zgarmagani holda elektronkovak jufti to‘xtovsiz hosil bo‘lib tursada, yarimo‘tkazgichda erkin zaryad tashuvchilar soni o‘zgarmaydi.
8. Germaniyga fosfor, rux, kaliy kiritilsa, qanday turdagi o‘tkazuvchanlik hosil bo‘ladi?
9. Nima sababdan bir xil kuchlanishda to‘g‘ri p–n o‘tishdagi tok, teskari o‘tishdagi tokka nisbatan ancha katta bo‘ladi?
10. Termistor (qarshiligi temperaturaga qarab o‘zgaradigan yarim o‘kazgichli asbob) uchiga ketma-ket holda 1 kΩ li qarshilik ulanib, unga 20 V kuchlanish berildi. Xona temperaturasida zanjirdagi tok kuchi 5 mA edi. Termistorni issiq suvga tushirilganda undan o‘tuvchi tok kuchi 10 mA bo‘lib qoldi. Termistor qarshiligi necha marta kamaygan? (Javobi: 3 marta). IX bobni yakunlash yuzasidan test savollari
1. Gapni to‘ldiring. Metallarning qizishi tufayli ulardan elektron uchib chiqish hodisasiga ... deyiladi.
A) ... termoelektron emissiya...; B). ..elektron emissiya...;
C) ...chiqish ishi...; D) ...to‘yinish toki....
2. Vakuumda elektr tokining tabiati nimadan iborat?
A) elektronlar oqimining bir tomonga harakatidan;
B) musbat ionlarning bir tomonga harakatidan;
C) manfi y ionlar oqimining bir tomonga harakatidan;
D) elektronlar, musbat va manfi y ionlarning bir tomonga harakatidan iborat.
3. Donor aralashmali yarimo‘tkazgichlar qanday turdagi o‘tkazuvchanlikka ega?
A) asosan elektron o‘tkazuvchanlikka;
B) asosan teshikli o‘tkazuvchanlikka;
C) teng miqdorda elektron va teshikli o‘tkazuvchanlikka;
D) elektr tokini o‘tkazmaydi.
4. Toza yarimo‘tkazgichdan elektronlarning tartibli harakati tufayli 1 mA tok o‘tmoqda. Yarimo‘tkazgichdan o‘tayotgan to‘la tok kuchi nimaga teng?
A) I mA; B) 2 mA; C) 0,5 mA; D) 0.
5. Gapni davom ettiring. “Temperatura ortishi bilan yarim o‘tkazgichning qarshiligi...”
A) ... ortadi; B) ... avval ortadi, so‘ngra kamayadi; C) ... kamayadi; D) ... avval kamayadi, so‘ngra ortadi.
6. Yarimo‘tkazgichda teshik va elektron uchrashganda nima hosil bo‘ladi?
A) musbat ion; B) neytral atom;
C) manfi y ion; D) musbat va manfi y ionlar.
7. Aralashmali o‘tkazuvchanlik qanday zarralarning harakati bilan bog‘langan?
A) asosan erkin elektronlar;
B) asosan kovaklar;
C) teng miqdordagi erkin elektronlar va kovaklar;D) turli miqdordagi erkin elektronlar yoki kovaklar.
8. “To‘g‘ri p–n o‘tishda yarimo‘tkazgichdagi berkituvchi qatlam ...” Gapni davom ettiring.
A) ... kengayadi;
B) ... torayadi;
C) ... o‘zgarmasdan qoladi;
D) ... kuchlanish kattaligiga qarab chiziqli o‘zgaradi.
9. Kovalent bog‘lanishda nechta elektron qatnashadi?
A) 1 ta; B) 2 ta; C) 3 ta; D) 4 ta.
10. n–p–n turdagi tranzistor bazasiga emitterga nisbatan qanday ishoradagi potensial berilganda tranzistordan tok o‘tadi?
A) musbat; C) nol;
B) manfi y; D) qanday ishorada berilishining ahamiyati yo‘q.
|
Termoelektron emissiya |
Metallarning qizishi tufayli ulardan elektron uchib chiqish hodisasi. |
|
Vakuumda elektr toki |
Elektronlar ionlar oqimining bir tomonga harakatidan iborat. |
|
Ikki elektrodli elektron lampa |
Anod va katoddan iborat vakuumli lampa – diod. |
|
To‘yinish toki |
Katoddan uchib chiqayotgan barcha elektronlar anodga yetib borganda anod tokining o‘zgarmay qolishi. |
|
Boguslavskiy- Lengmyur formulasi |
Ia = kU 3/2. Vakuumli dioddan o‘tuvchi tok kuchining anod kuchlanishiga bog‘liqligi. |
|
Metall o‘tkazgichlar qarshiliklarining temperaturaga bog‘liqligi |
R = R0(1 + αt); R0 –0o C da o‘tkazgich qarshiligi; R– t temper aturadagi qarshiligi, α – qarshilikning temperatura koeffi tsiyenti. |
|
O‘ta o‘tka zuv chanlik |
Temperatura pasayishi bilan o‘tkazgich qarshiligining keskin kamayib nolga tushib qolishi. |
|
Elektron o‘tkazuvchanlik (n-turdagi o‘tkazuvchanlik) |
Erkin elektronlarning ko‘chishi tufayli yarimo‘tkazgichda tok hosil bo‘lishi. |
|
Kovakli o‘tkazuvchanlik (p – turdagi o‘tkazuvchanlik) |
Kovalent bog‘lanishda elektron yetishmasligi tufayli hosil bo‘lgan bo‘sh o‘ringa kovak deyiladi. Elektr maydoni ta’sirida kovaklarning ko‘chishi tufayli yarimo‘tkazgichda kovakli o‘tkazuvchanlik ro‘y beradi. |
|
Yarimo‘tkazgichlarda xususiy o‘tkazuvchanlik |
Yarimo‘tkazgichdan teng miqdorda erkin elektronlar va kovaklar ko‘chishi tufayli elektr tokini o‘tkazishi. |
|
Donorli aralashmalar |
Sof yarimo‘tkazgichga qo‘shilganda osongina elektronini beradigan aralashmalar. Bunda n-turdagi o‘tka zuv chanlik hosil boladi. |
|
Akseptorli aralashmalar |
Sof yarimo‘tkazgichga qo‘shilganda kovalent bog‘lanish uchun bitta elektroni yetishmasdan kovak hosil qiladigan aralashmalar. Bunda p-turdagi o‘tkazuvchanlik hosil bo‘ladi. |
|
Berkituvchi qatlam |
Bir tomoni n-turdagi, ikkinchi tomoni p-turdagi yarimo‘tkazgich chegarasida hosil bo‘ladigan zaryadli zarralar bo‘lmagan soha. |
|
To‘g‘ri p–n o‘tish |
Bir tomoni n-turdagi, ikkinchi tomoni p-turdagi yarimo‘tkazgichda p-sohasini manbaning musbat qutbiga, n-sohasini manfi y qutbiga ulanganda berkituvchi qatlam yupqalashib, tok o‘tishi. |
|
Teskari p–n o‘tish |
Bir tomoni n-turdagi, ikkinchi tomoni p-turdagi yarimo‘tkazgichda p-sohasini manbaning manfi y qutbiga, n-sohasini manbaning musbat qutbiga ulanganda berkituvchi qatlam kengayib, tok o‘tmasligi. |
|
Yarimo‘tkazgichli diod |
Bitta
p–n o‘tishga ega bo‘lgan yarimo‘tkazgichli asbob. Shartli belgisi |
|
Tranzistor |
Ikkita p–n o‘tishga ega bo‘lgan yarimo‘tkazgichli asbob. p–n–p va n–p–n strukturalarda bo‘ladi. |
|
Integral mikrosxema (IMS) |
Elektr zanjiri juda yuqori darajada zichlashtirib ulangan elementlardan tashkil topgan mikroelektron qurilma. IMSga ulangan elementlar soni ~106 gacha bo‘ladi. |
1. Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики/ М.М.Балашов и др.; под ред. Г.Я. Мякишева. – 5-е изд.стереотип. – М.: “Дрофаˮ, 2002. – 496 с.: ил.
2. Физика: Электродинамика. 10 – 11 кл.: Учеб. для углубленного изучения физики/ Г.Я. Мякишев, А.З. Синяков, Б. А. Слободсковa. – 4-е изд. стереотип. – М.: “Дрофаˮ, 2002. – 480 с.: ил.
3. Физика. 10 кл.: Учеб.для общеобразоват. учеб.заведений. – 4-е изд. стереотип. – М.: “Дрофаˮ, 2001. – 416 с.: ил.
4. N.Sh. Turdiyev. Fizika. Fizika fani chuqur o‘rganiladigan umumta’lim maktab larining 7-sinfi uchun darslik. – T.: Gafur G‘ulom nomidagi nashriyot-matbaa ijodiy uyi, 2016.
5. N.Sh. Turdiyev. Fizika. Umumta’lim maktablarining 8-sinfi uchun darslik. – T.: “TuronIqbolˮ, 2006.
6. Ўзбекистон Миллий энциклопедияси. – Т.: “Ўзбекистон Миллий энциклопедияси” Давлат илмий нашриёти, 2004.
7. Физика. Энциклопедия/ под. ред. Ю.В. Прохорова. – М.: Большая Российс кая энциклопедия, 2003. – 944 с.
8. A. No‘monxojayev va b. Fizika 1. – T.: “O‘qituvchiˮ.– 2002. – 400 b.
9. A. No‘monxo‘jayev va b. Fizika II. – T.: “O‘qituvchiˮ– 2003. – 414 b.
10. A. No‘monxo‘jayev va b. Fizika III. – T.: “O‘qituvchiˮ– 2001. – 352 b.
11. K.A. Tursunmetov, A.M. Xudoyberganov. Fizikadan praktikum. – T.: “O‘qituvchiˮ 2003.
12. K.A. Tursunmetov va b. Fizikadan masalalar to‘plami. – T.: “O‘qituvchiˮ 2004.
13. K.A. Tursunmetov va b. Fizika. Ma’lumotnoma. – T.: “O‘zbekistonˮ. 2016. – 202 b.
14. K. Suyarov, Sh. Usmonov, J. Usarov. Fizika (Mexanika). 1-kitob. O‘qituvchiga yordamchi qo‘llanma: T.: “Yangi nashr” nashriyoti, – 2010.
15. A. G. Ganiyev, A. K. Avliyoqulov, G. A. Alimardonova. Fizika. I gism. Akademik litsey va kasb-hunar kollejlari uchun darslik. – T.: “O‘qituvchiˮ 2012. – 400 b.
16. A. G. Ganiyev, A. K. Avliyoqulov, G. A. Alimardonova. Fizika. II gism. Akademik litsey va kasb-hunar kollejlari uchun darslik. – T.: “O‘qituvchiˮ 2013. – 208 b.
17. К. Суяров, А. Хусанов, Л. Худойбердиев. Физика. Механика ва молекуляр физика./I китоб. – T.: “O‘qituvchiˮ.– 2002.
18, L. Xudoyberdiyev, A. Husanov, A. Yunusov, J. Usarov. Fizika. Elektrodinamika.
Elektromagnit tebranishlar 2-kitob. – T.: “O‘qituvchiˮ NMIU.– 2004.

MEXANIKA .................................................................................................................................... 3
1-mavzu. Fizikaning tadqiqot metodlari .................................................................................. 3 I bob. KINEMATIKA .................................................................................................................... 5 2-mavzu. Mexanik harakat turlari. Harakatlarning mustaqillik prinsipi ................................ 5 3-mavzu. Jismlarning vertikal harakati .................................................................................... 7 4-mavzu. Aylana bo‘ylab notekis harakat. Burchak tezlanish. Tangensial tezlanish. .......... 10 5-mavzu. Aylanma va ilgarilanma harakatni o‘zaro uzatish ..................................................14 6-mavzu. Gorizontal otilgan jism harakati .............................................................................16 7-mavzu. Gorizontga qiya otilgan jism harakati .....................................................................18 8-mavzu. Laboratoriya ishi: Gorizontga qiya otilgan jism harakatini o‘rganish. ................. 22 I bobni yakunlash yuzasidan test savollari ............................................................................ 24
I bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar ............................................ 25
II bob. DINAMIKA ...................................................................................................................... 28 9-mavzu. Dinamika qonunlari ................................................................................................ 28
10-mavzu. Galileyning nisbiylik prinsipi. Inersial va noinersial sanoq sistemalari ............. 32 11-mavzu. Gravitatsion maydonda harakat ............................................................................ 35 12-mavzu. Jism og‘irligining harakat turiga bog‘liqligi ........................................................ 37 13-mavzu. Jismning bir necha kuch ta’siridagi harakati ....................................................... 40 II bobni yakunlash yuzasidan test savollari ...........................................................................44
II bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar .......................................... 45
III bob. MEXANIKADA SAQLANISH QONUNLARI .......................................................... 47
14-mavzu. Energiya va ish. Energiyaning saqlanish qonuni. Jismning qiya tekislik
bo‘ylab harakatlanishida bajarilgan ish ......................................................................... 47 15-mavzu. Laboratoriya ishi: Qiya tеkislikda foydali ish koeffi tsiyеntini aniqlash ..............51 16-mavzu. Jismlarning absolyut elastik va noelastik to‘qnashishi ........................................ 53 III bobni yakunlash yuzasidan test savollari ......................................................................... 57
III bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar ......................................... 58
IV bob. STATIKA VA GIDRODINAMIKA .............................................................................. 59 17-mavzu. Jismlarning muvozanatda bo‘lish shartlari ........................................................... 59 18-mavzu. Momentlar qoidasiga asoslanib ishlaydigan mexanizmlar .................................. 62 19-mavzu. Aylanma harakat dinamikasi ................................................................................ 65
20-mavzu. Suyuqlik va gazlar harakati, oqimning uzluksizlik teoremasi.
Bernulli tenglamasi ........................................................................................................ 68
21-mavzu. Harakatlanayotgan gazlar va suyuqliklarda bosimning tezlikka
bog‘liqligidan texnikada foydalanish ............................................................................. 71 IV bobni yakunlash yuzasidan test savollari ......................................................................... 75
IV bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar ......................................... 76
V bob. MEXANIK TEBRANISHLAR VA TO‘LQINLAR .................................................... 78
22-mavzu. Garmonik tebranishlar. ......................................................................................... 78 23-mavzu. Prujinali va matematik mayatniklar ..................................................................... 81
24-mavzu. Laboratoriya ishi: Matematik mayatnik yordamida erkin tushish
tezlanishini aniqlash ....................................................................................................... 85
25-mavzu. Majburiy tebranishlar. Texnikada rezonans ......................................................... 86
26-mavzu. Mexanik to‘lqinlarning muhitlarda tarqalishi. Ultra va infratovushlardan
turmushda va texnikada foydalanish ............................................................................. 90 V bobni yakunlash yuzasidan test savollari ........................................................................... 95
V bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar .......................................... 96
VI bob. TERMODINAMIKA ASOSLARI ................................................................................ 98 27-mavzu. Issiqlik jarayonlarining qaytmasligi. Termodinamika qonunlari ........................ 98 28-mavzu. Adiabatik jarayon. Issiqlik mashinasining foydali ish koeffi tsiyenti.
Karno sikli .................................................................................................................... 102
29-mavzu. Inson hayotida issiqlik divigatellarining ahamiyati.
Issiqlik dvigatellari va ekologiya ................................................................................. 106 VI bobni yakunlash yuzasidan test savollari ........................................................................112
VI bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar ........................................112
VII bob. ELEKTRODINAMIKA...............................................................................................114
30-mavzu. Zaryadning saqlanish qonuni. Nuqtaviy zaryadning maydoni.
Elektr maydon kuchlanganligining superpozitsiya prinsipi ........................................114 31-mavzu. Zaryadlangan sharning elektr maydoni. Dielektrik singdiruvchanlik ...............118 32-mavzu. Nuqtaviy zaryad maydonining potensiali. Potensiallar farqi ............................ 120 33-mavzu. Elektrostatik maydonda zaryadni ko‘chirishda bajarilgan ish .......................... 123 34-mavzu. Elektr maydon energiyasi ................................................................................... 125 VII bobni yakunlash yuzasidan test savollari ...................................................................... 129
VII bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar ..................................... 130
VIII bob. O‘ZGARMAS TOK QONUNLARI .........................................................................132 35-mavzu. Elektr o‘tkazuvchanlik. Tok kuchining kuchlanishga bog‘liqligi ......................132 36-mavzu. Tok kuchi va tok zichligi. Elektr tokining ta’sirlari .......................................... 136 37-mavzu. Butun zanjir uchun Om qonuni. Tok manbayining foydali ish koeffi tsiyenti ...138 38-mavzu. Tok manbalarini ketma-ket va parallel ulash ......................................................141 39-mavzu. Ampermetr va voltmetrning o‘lchash chegarasini oshirish ...............................145 40-mavzu. Laboratoriya ishi: Tok manbayining EYuK va ichki qarshiligini aniqlash ......147
VIII bobni yakunlash yuzasidan test savollari .....................................................................149
VIII bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar .................................... 150
IX bob. TURLI MUHITLARDA ELEKTR TOKI .................................................................152
41-mavzu. Vakuumda elektr toki ...........................................................................................152 42-mavzu. Metall o‘tkazgichlar qarshiligining temperaturaga bog‘liqligi ......................... 154 43-mavzu. Yarimo‘tkazgichlarda xususiy o‘tkazuvchanlik. Aralashmali o‘tkazuvchanlik ...157
44-mavzu. Yarimo‘tkazgichli asboblar (diod, tranzistor) va ularning
texnikada qo‘llanilishi ...................................................................................................161
45-mavzu. Laboratoriya ishi: Yarim otkazgichli diodning volt-amper
xarakteristikasini o‘rganish ...........................................................................................166 IX bobni yakunlash yuzasidan test savollari ........................................................................168
IX bobda o‘rganilgan eng muhim tushuncha, qoida va qonunlar ........................................170
FOYDALANILGAN ADABIYOTLAR ....................................................................................172
F58 Fizika. O‘rta ta’lim muassasalarining 10-sinfi va o‘rta maxsus, kasbhunar ta’limi muassasalarining o‘quvchilari uchun darslik /N. Sh. Turdiyev, K. A. Tursunmetov, A. G. Ganiyev, K. T. Suyarov, J. E. Usa rov, A. K. Avliyoqulov. – T.: “Niso Poligraf” nashriyoti, 2017. – 176 b.
ISBN 978-9943-4867-6-8 UO‘K: 53(075.3)
KBK22.3ya721
O‘quv nashri
Narziqul Sheronovich Turdiyev, Komiljon Axmetovich Tursunmetov,
Abduqahhor Gadoyevich Ganiyev, Kusharbay Tashbayevich Suyarov, Jabbor Eshbekovich Usarov, Abdurashit Karimovich Avliyoqulov
F I Z I K A
O‘rta ta’lim muassasalarining 10-sinfi va o‘rta maxsus, kasb-hunar ta’limi muassasalarining o‘quvchilari uchun darslik
1-nashri
Mas’ul muharrir Z. Sangirova
Muharrir M. Po‘latov
Rasmlar muharriri J. Gurova
Texnik muharrir D. Salixova
Kompyuterda tayyorlovchi E. Kim
Original-maket “NISO POLIGRAF” nashriyotida tayyorlandi. Toshkent viloyati, O‘rta Chirchiq tumani, “Oq-Ota” QFY, Mash’al mahallasi, Markaziy ko‘chasi, 1-uy.
Litsenziya raqami AI № 265.24.04.2015.
Bosishga 2017-yil 11-avgustda ruxsat etildi. Bichimi 70 × 100 1/16.
Ofset qog‘ozi. “Times New Roman” garniturasi. Kegli 12,5.
Shartli bosma tabog‘i 12,87. Nashr tabog‘i 12,76.
Adadi 428121 nusxa. 186-sonli shartnoma. 17-625-sonli buyurtma.
O‘zbekiston Matbuot va axborot agentligining “O‘zbekiston” nashriyot-matbaa ijodiy uyida bosildi.
100011, Toshkent, Navoiy ko‘chasi, 30.
Ijaraga berilgan darslik holatini ko‘rsatuvchi jadval
|
T/r |
O‘quv chining ismi, familiyasi |
O‘quv yili |
Darslikning olingandagi holati |
Sinf rahbarining imzosi |
Darslikning topshi rilgandagi holati |
Sinf rahbari- ning imzosi |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
Darslik ijaraga berilib, o‘quv yili yakunida qaytarib olinganda yuqoridagi jadval sinf rahbari tomonidan quyidagi baholash mezonlariga asosan to‘ldiriladi:
Turdiyev, Narziqul Sheronovic
T–95 Fizika: umumiy o‘rta ta’lim lik. /N. Sh. Turdiyev, K. A. Tursu J. E. Usar ov, A. K. Avliyoqulov – T 2017. – 176 b.
ISBN
Narziqul Sheronovich Turdiyev, K
A.G. Ganiyev, Nu
Jabbor Eshbekovich Usaro
F I Z
Umumiy o‘rta ta’lim maktab
Muharrir Sh
Rasmlar muh
Texnik muha
Kompyuterda ta
Original-maket “NISO POLIG Toshkent viloyati, O‘rta Ch Mash’al mahallasi, M
Litsenziya raqami
Bosishga 2017-yil 2-mayda r
Ofset qog‘ozi. “Times New R
Shartli bosma tabog‘i 1
Adadi 474300 nusxa. 107-sonli s
O‘zbekiston Matbuot va axborot agentligining “O
100011, Toshkent
|
Yangi |
Darslikning birinchi marotaba foydalanishga berilgandagi holati. |
|
Yaxshi |
Muqova butun, darslikning asosiy qismidan ajralmagan. Barcha varaqlari mavjud, yirtilmagan, ko‘chmagan, betla rida yozuv va chiziqlar yo‘q. |
|
Qoniqarli |
Muqova ezilgan, birmuncha chizilib, chetlari yedirilgan, darslikning asosiy qismidan ajralish holati bor, foyda lanuvchi tomonidan qoniqarli ta’mirlangan. Ko‘chgan varaqlari qayta ta’mirlangan, ayrim betlariga chizilgan. |
|
Qoniqarsiz |
Muqovaga chizilgan, yirtilgan, asosiy qismidan ajralgan yoki butunlay yo‘q, qoniqarsiz ta’mirlangan. Betlari yirtilgan, varaqlari yetishmaydi, chizib, bo‘yab tashlangan. Darslikni tiklab bo‘lmaydi. |
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.