Физика_9класс_Кинематика_дидактический материал (2) (1)

Приложение 1.    Теоретический материал к  уроку по теме «Скорость при прямолинейном равноускоренном движении»

Нам известно, что при прямолинейном равноускоренном движении ускорение тела можно рассчитать по формуле

Выразим из этой формулы скорость, которую могло бы иметь тело в конце промежутка времени Δt.

Получим

Или

Мы получили формулу, которая называется уравнением скорости при равноускоренном движении.

Напомним, что по формулам, записанным в векторном виде, вычисления вести нельзя.

Перепишем нашу формулу в проекции на ось х.

Таким образом, зная проекцию вектора начальной скорости и проекцию вектора ускорения, можно вычислить проекцию вектора мгновенной скорости, которую будет иметь тело к концу любого заданного промежутка времени.

Представим зависимость проекции вектора скорости от времени при равноускоренном движении в виде графика.

Из курса математики вам известна линейная функция

у = kx + b,

где х — аргумент, k — постоянный коэффициент, b — свободный член. Графиком этой функции является прямая линия.

Функция

υ_x = υ_0x + a_xΔt

тоже линейная с аргументом Δt, постоянным коэффициентом а_х и свободным членом υ_0х. Значит, графиком этой функции тоже должна быть прямая линия. Расположение этой линии по отношению к осям координат определяется значениями проекции начальной скорости и ускорения.

Рассмотрим, какой вид будет иметь график скорости в зависимости от знаков проекций ускорения и начальной скорости.

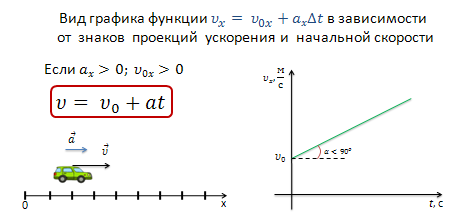
Если проекция вектора скорости тела и его ускорение направлены по оси Ох, то уравнение примет вид

В этом случае скорость тела с течением времени возрастает. При этом график скорости образует с положительным направлением оси t острый угол.

Если же проекция вектора скорости тела и его ускорение направлены против оси Ох, то уравнение примет вид

Скорость тела с течением времени возрастает, но тело, при этом, движется в отрицательном направлении. График скорости образует с положительным направлением оси t тупой угол.

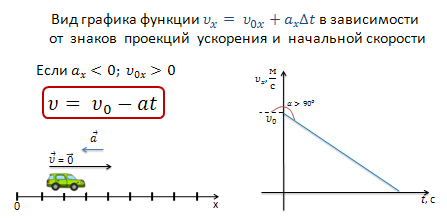
В случае, если скорость тела направлена по оси Ох, а ускорение — против оси Ох, то формула принимает вид

Скорость тела убывает от некоторого значения до нуля. График скорости образует с положительным направлением оси t тупой угол.

Когда ускорение направлено по оси х, а начальная скорость против оси х, то формула принимает вид:

скорость тела с течением времени возрастает. Но при этом график скорости образует с положительным направлением оси t тупой угол.

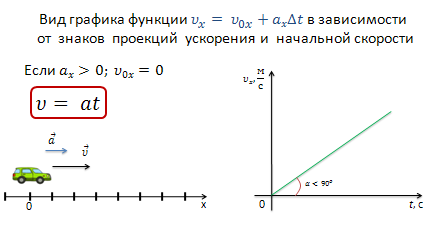
Если в начальный момент времени тело покоилось, то уравнение примет вид

если проекция вектора ускорения направлена по оси Ох, то скорость тела возрастает и график скорости, в этом случае, образует с положительным направлением оси t острый угол и начинается в точке (0;0).

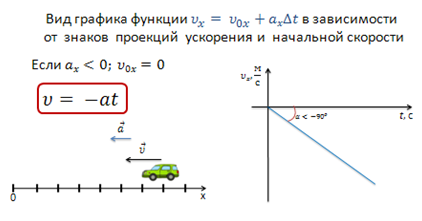
Или

если проекция вектора ускорения направлена против оси х. Скорость тела возрастает, но при этом тело движется в отрицательном направлении, но так же начинается в точке (0;0).

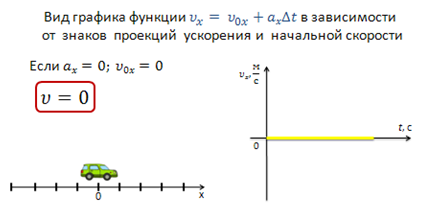
И последнее, если проекции начальной скорости и ускорения равны нулю, то тело с течением времени не изменяет своего положения и графиком скорости является прямая, совпадающая с осью времени (тело покоится).