Фонд оценочных средств по учебному предмету "Геометрия" 8 класс

Муниципальное бюджетное общеобразовательное учреждение

основная общеобразовательная школа с. Волочаевка

 

Рассмотрен на заседании педагогического совета Протокол №___от ___________________

Согласовано Заместитель директора по УВР _________/_________________

Утверждаю: Директор МБОУ ООШ с. Волочаевка _________/_______________ Приказ № ___ от _______________________

 

 

 

 

Фонд оценочных средств по учебному предмету «Геометрия»

8 класс

 

 

 

 

 

 

Составитель:

Сульдина Н.А.,

учитель начальных классов

 

 

Волочаевка, 2020

Паспорт фонда оценочных средств по геометрии

8 класс

№ п/п	Контролируемые разделы (темы) предмета	Наименование оценочных средств
1	Четырехугольники	Контрольная работа №1 по теме «Четырёхугольники».
		Тест №1 по теме «Четырёхугольники».
2	Площадь	Контрольная работа №2 по теме «Теорема Пифагора. Площадь».
		Тест №2 по теме «Теорема Пифагора. Площадь».
3	Подобные треугольники	Контрольная работа №3 по теме «Соотношение между сторонами и углами прямоугольного треугольника».
		Тест №3 по теме «Соотношение между сторонами и углами прямоугольного треугольника».
4	Окружность	Контрольная работа №4 по теме «Окружность».
		Тест №4 по теме «Окружность».
Всего оценочных средств – 8

 

 

 

 

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Контрольная работа №1 по теме «Четырёхугольники».

Вариант I

1. Диагонали прямоугольника АВСD пересекаются в точке О. Найдите угол между диагоналями, если АВО = 30°.

2. В параллелограмме KМNP проведена биссектриса угла МKР, которая пересекает сторону MN в точке Е.

а) Докажите, что треугольник KМЕ равнобедренный.

б) Найдите сторону KР, если МЕ = 10 см, а периметр параллелограмма равен 52 см.

Вариант II

1. Диагонали ромба KМNP пересекаются в точке О. Найдите углы треугольника KОМ, если угол МNP равен 80°.

2. На  стороне  ВС  параллелограмма  АВСD  взята  точка  М  так,  что АВ = ВМ.

а) Докажите, что АМ – биссектриса угла ВАD.

б) Найдите периметр параллелограмма, если СD = 8 см, СМ = 4 см.

Вариант III

1. Через вершину С прямоугольника АВСD проведена прямая, параллельная диагонали ВD и пересекающая прямую АВ в точке М. Через точку М проведена прямая, параллельная диагонали АС и пересекающая прямую ВС  в  точке  N.  Найдите периметр четырехугольника АСМN, если диагональ ВD равна 8 см.

2. Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке М, лежащей на стороне ВС. Луч DМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСD, если АN = 10 см.

Критерии оценивания:

Оценка «5» - правильное выполнение двух задач; (3 задание на дополнительную оценку)

Оценка «4»  - имеются вычислительные ошибки, с их учетом дальнейшее решение правильное;

Оценка «3»  - решение двух  задач  неполное, есть вычислительные ошибки;

Оценка «2» -  нет решения ни одной задачи.

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Тест №1 по теме «Четырёхугольники».

Вопрос №1

Выберите верный ответ.

Сумма углов равна 360º:

A) в прямоугольнике.

B) в трапеции.

C) в ромбе.

D) во всех перечисленных выше фигурах.

Вопрос №2

Выберите правильное определение параллелограмма.

A) Параллелограммом называется четырехугольник, у которого стороны попарно параллельны.

B) Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.

C) Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Вопрос №3

Выберите верные варианты ответа.

По первому свойству в параллелограмме

A) противоположные стороны и углы равны.

B) противоположные стороны равны.

C) противоположные углы равны.

D) диагонали равны.

Вопрос №4

Выберите верное утверждение.

По второму свойству параллелограмма

A) диагонали равны.

B) диагонали пересекаются пополам.

C) диагонали точкой пересечения делятся пополам.

Вопрос №5

Выберите верные утверждения.

По признаку параллелограмма 

A) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

B) Если в четырехугольнике противоположные стороны равны, то этот четырехугольник – параллелограмм.

C) Если в четырехугольнике две стороны равны, то этот четырехугольник – параллелограмм.

D) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

E) Если в четырехугольнике диагонали равны, то этот четырехугольник – параллелограмм.

F) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Вопрос №6

Вставьте пропущенные слова в определение.

Трапецией называется четырехугольник, у которого две стороны _____________________, а две другие ____________________.

Вопрос №7

Выберите верный ответ.

Если боковые стороны трапеции равны, то её называют:

A) правильной,

B) равнобокой,

C) прямоугольной.

Вопрос №8

Выберите верное утверждение.

A) Прямоугольником называется четырехугольник, у которого все углы прямые.

B) Прямоугольником называется параллелограмм, у которого все углы прямые.

C) Прямоугольником называется четырехугольник, у которого два угла прямые.

D) Прямоугольником называется четырехугольник, у которого углы прямые.

E) Прямоугольником называется параллелограмм, у которого противоположные углы прямые.

Вопрос №9

Выберите утверждение, которое является признаком прямоугольника.

A) Диагонали прямоугольника равны.

B) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

C) Прямоугольником называется параллелограмм, у которого все углы прямые.

Вопрос №10

Параллелограмм, у которого все стороны равны называется _________________.

Вопрос №11

Выберите верные утверждения, которые являются свойствами ромба.

A) Диагонали ромба равны.

B) Диагонали ромба взаимно перпендикулярны.

C) диагонали ромба пересекаются и точкой пересечения делятся пополам.

D) Диагонали ромба делят его углы пополам.

Вопрос №12

Выберите верное утверждение.

A) Квадратом называется четырехугольник, у которого все стороны равны.

B) Квадратом называется параллелограмм, у которого все углы прямые.

C) Квадратом называется прямоугольник, у которого все стороны равны.

Вопрос №13

Выберите верный ответ.

Свойством квадрата является.

A) Все углы квадрата прямые.

B) Диагонали квадрата равны.

C) Диагонали квадрата взаимно перпендикулярны.

D) Диагонали квадрата точкой пересечения делятся пополам.

E) Диагонали квадрата делят его углы пополам.

F) Каждое выше перечисленное утверждение.

Критерии оценивания:

 

менее 5 заданий – оценка «2»

5 – 7 заданий – оценка «3»

8 – 10 заданий – оценка «4»

11 – 13 заданий – оценка «5»

Правильные ответы, решения к тесту:

Вопрос №1

Правильный ответ — D

Вопрос №2

Правильный ответ — C

Вопрос №3

Правильный ответ — B, C

Вопрос №4

Правильный ответ — C

Вопрос №5

Правильный ответ — A, D, F

Вопрос №6

Правильный ответ — параллельны, не параллельны

Вопрос №7

Правильный ответ — B

Вопрос №8

Правильный ответ — A, B, E

Вопрос №9

Правильный ответ — B

Вопрос №10

Правильный ответ — ромбом

Вопрос №11

Правильный ответ — B, C, D

Вопрос №12

Правильный ответ — C

Вопрос №13

Правильный ответ — F

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Контрольная работа №2 по теме «Теорема Пифагора. Площадь».

 Вариант I

1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.

2. Площадь  прямоугольной  трапеции  равна  120 см²,  а  ее  высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.

3. На стороне АС данного треугольника АВС постройте точку D так, чтобы площадь треугольника АВD составила одну треть площади треугольника АВС.

Вариант II

1. Одна  из  диагоналей  параллелограмма  является  его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см².

2. Найдите  площадь  трапеции  АВСD  с  основаниями  АD и ВС, если АВ = 12 см, ВС = 14 см, АD = 30 см, В = 150°.

3. На продолжении стороны KN данного треугольника KМN постройте точку Р так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KМN.

Критерии оценивания:

Оценка «5» - правильное выполнение двух задач; (3 задание на дополнительную оценку)

Оценка «4»  - имеются вычислительные ошибки, с их учетом дальнейшее решение правильное;

Оценка «3»  - решение двух  задач  неполное, есть вычислительные ошибки;

Оценка «2» -  нет решения ни одной задачи.

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Тест №2 по теме «Теорема Пифагора. Площадь».

1.                 Задание: Соответствие между названием фигуры и формулой нахождения её площади

А) квадрат	1.
Б) прямоугольник	2.
В) треугольник	3.
Г) параллелограмм	4.
Д) трапеция	5.

А	Б	В	Г	Д

 

 

 

2.                 Задание: Отметьте правильный ответ

Площадь квадрата со стороной  5,3 см равна

а) 28,09 см²

б) 10,6 см²

в) 27,09 см²

г) 29,09 см²

3.                 Задание: Отметьте правильный ответ

Прямоугольник площадью 91,44 см² и шириной 7,2 см имеет длину

а) 13,7 см

б) 12,61 см

в) 12,7 см

г) 14,1 см

4.                 Задание: Отметьте правильный ответ

Площадь параллелограмма, изображённого на рисунке 1, равна

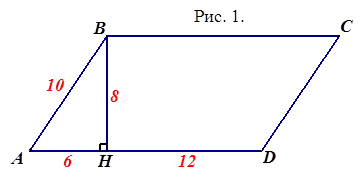а) 96

б) 144

в) 48

г) 180

 

5.                 Задание: Отметьте правильный ответ

Площадь треугольника, изображённого на рисунке 2, равна

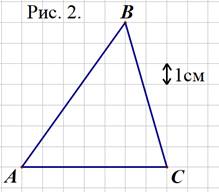а) 24,5 см²

б) 49 см²

в) 35 см²

г) 24,5 см

 

 

 

 

6.                 Задание: Дополните

Площадь трапеции, изображённой на рисунке 3, равна … ед².

 

 

 

 

 

 

 

 

 

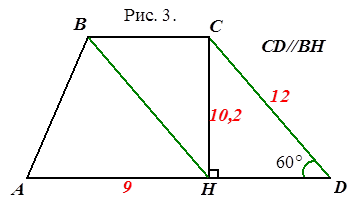
7.                 Задание: Дополните

Площадь ромба, изображённого на рисунке 4, равна … см²

 

 

 

 

 

 

 

 

 

8.                 Задание: Дополните

Площадь серой части фигуры, изображённой на рисунке 5, равна … ед².

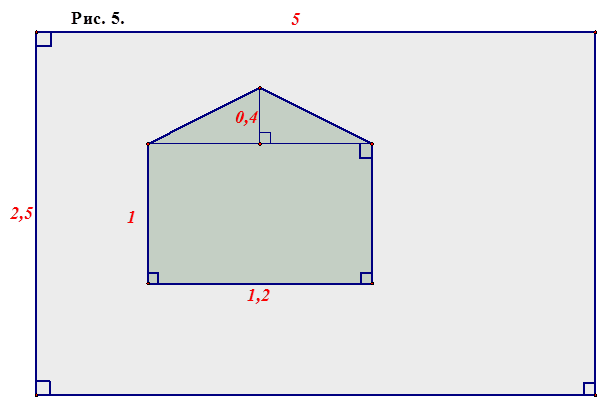
9.     Задание: Дополните

Площадь жёлтой части фигуры, изображённой на рисунке 6 равна … дм²

 

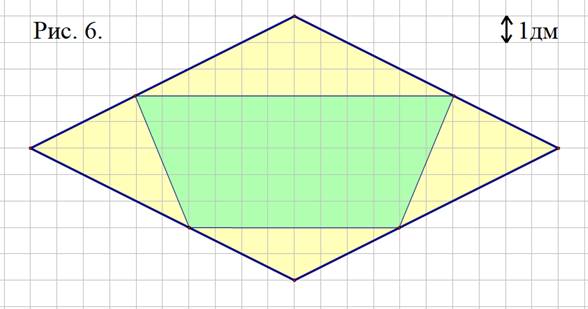
10.            Задание: Отметьте правильный ответ

Площадь ромба вычисляется по формуле

а)

б)

в)

г)

Критерии оценивания:

 

менее 5 заданий – оценка «2»

5 – 6 заданий – оценка «3»

7 – 8 заданий – оценка «4»

9 – 10 заданий – оценка «5»

 

 

              

КЛЮЧ

№	1	2	3	4	5	6	7	8	9	10
ответ	23154	а	в	б	а	107,1	80	9,81	50	б, д

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Контрольная работа №3 по теме «Соотношение между сторонами и углами прямоугольного треугольника».

Вариант I

1. На рисунке 1 АВ || СD. а) Докажите, что АО : ОС = ВО : ОD. б) Найдите АВ, если ОD = 15 см, ОВ = 9 см, СD = 25 см.

2. Найдите  отношение  площадей  треугольников  АВС  и  KMN,  если АВ = 8 см, ВС = 12 см, АС = 16 см, KM = 10 cм, MN = 15 см, NK = 20 см.

Вариант II

1. На рисунке 2 MN || АС. а) Докажите, что АВ · BN = CВ · BM. б) Найдите MN, если AM = 6 см, ВM = 8 см, АС = 21 см.

2. Даны стороны треугольников PQR и АВС: PQ = 16 см, QR = 20 см, PR = 28 см и АВ = 12 cм, ВС = 15 см, АС = 21 см. Найдите отношение площадей этих треугольников.

 

 Критерии оценивания:

Оценка «5» - правильное выполнение двух задач; (3 задание на дополнительную оценку)

Оценка «4»  - имеются вычислительные ошибки, с их учетом дальнейшее решение правильное;

Оценка «3»  - решение двух  задач  неполное, есть вычислительные ошибки;

Оценка «2» -  нет решения ни одной задачи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Тест №3 по теме «Подобные треугольники».

 Вопрос №1

Выберите верные утверждения.

Отрезки АВ и CD пропорциональны отрезкам  KL и MN, если:

A) можно составить отношения этих отрезков;

B) можно составить равные отношения из этих отрезков;

C)  АВKL и C​DMN соответственно; 

D) из них можно составить пропорцию.

Вопрос №2

Выберите верное продолжение определения.

Два треугольника называются подобными, если

A) их углы равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

B) их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

C) их углы соответственно равны и каждая сторона одного треугольника пропорциональна каждой стороне другого треугольника.

Вопрос №3

Выберите верные утверждения.

Коэффициент подобия показывает

A) отношение сходственных сторон подобных треугольников;

B) разницу между сходственными сторонами подобных треугольников;

C) во сколько раз отличаются сходственные стороны подобных треугольников;

D) отношение сходственных углов подобных треугольников.

Вопрос №4

Выберите верное утверждение.

Отношение площадей двух подобных треугольников равно

A) 2k;

B) k²;

C) k;

D) .

Вопрос №5

Выберите первый признак подобия треугольников.

A) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

B) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то  такие треугольники подобны.

C) Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Вопрос №6

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

Выберите соответствующий номер признака подобия треугольников.

A) первый;

B) второй;

C) третий;

D) четвертый.

Вопрос №7

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Выберите соответствующий номер признака подобия треугольников.

A) четвертый;

B) третий;

C) второй;

D) нет верного номера.

Вопрос №8

Три угла одного треугольника соответственно равны трём углам другого треугольника.

Такие треугольники подобны по

A) определению подобных треугольников;

B) третьему признаку подобия;

C) первому признаку подобия.

Вопрос №9

Выберите верное утверждение.

Согласно второму признаку 

A) любые прямоугольные треугольники подобны;

B) любые равнобедренные прямоугольные треугольники подобны;

C) любые равнобедренные треугольники подобны.

Вопрос №10

Выберите верные утверждения.

A) Любые две окружности разного радиуса подобны.

B) Любые равнобедренные треугольники, имеющие по равному острому углу, подобны.

C) Любые прямоугольники подобны.

D) Любые равнобедренные треугольники, имеющие по равному тупому углу, подобны.

E) Любые квадраты подобны.

 

 

 

 

Критерии оценивания:

 

менее 5 заданий – оценка «2»

5 – 6 заданий – оценка «3»

7 – 8 заданий – оценка «4»

9 – 10 заданий – оценка «5»

 

Правильные ответы, решения к тесту:

Вопрос №1

Правильный ответ — B, D

Вопрос №2

Правильный ответ — B

Вопрос №3

Правильный ответ — A, C

Вопрос №4

Правильный ответ — B

Вопрос №5

Правильный ответ — C

Вопрос №6

Правильный ответ — B

Вопрос №7

Правильный ответ — B

Вопрос №8

Правильный ответ — C

Вопрос №9

Правильный ответ — B

Вопрос №10

Правильный ответ — A, D, E

 

 

 

 

 

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Тест №4 по теме «Окружность».

1.     Какие из утверждений верны?

1)    Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая пересекает окружность.

2)    Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

3)    Если прямая и окружность не имеют общих точек, то радиус окружности меньше расстояния от центра окружности до прямой.

2.     Какие из утверждений верны?

1)    Окружность это фигура, состоящая из точек плоскости, расположенных на одинаковом расстоянии от данной точки.

2)    Прямая и окружность имеют две общие точки, если радиус окружности больше расстояния от центра окружности до прямой.

3)    Радиус окружности это отрезок, соединяющий две точки окружности.

3.     Какие из утверждений верны?

1)    Радиус окружности больше диаметра этой окружности.

2)    Хорда окружности это отрезок, соединяющий две точки окружности.

3)    Диаметр это хорда, проходящая через центр окружности.

4.     Какие из утверждений верны?

1)    Круг это фигура, состоящая из множества точек плоскости, находящихся на расстоянии, не превышающем данного, от заданной точки плоскости.

2)    Касательная это прямая, имеющая с окружностью одну общую точку.

3)    Диаметр это отрезок, соединяющий две любые точки.

5.     Какие из утверждений верны?

1)    Касательная к окружности образует угол в 90⁰ с радиусом, проведённым в точку касания.

2)    Отрезки касательных к окружности, проведённые из одной точки, равны.

3)    Вписанный угол это угол, вершина которого совпадет с центром окружности.

6.     Какие из утверждений верны?

1)    Вписанный угол это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

2)    Центральный угол равен половине дуги, на которую опирается.

3)    Вписанный угол измеряется половиной дуги, на которую опирается.

7.     Какие из утверждений верны?

1)    Если центральный угол и вписанный опираются на одну и ту же дугу, то градусные меры их равны

2)    Вписанные углы, опирающиеся на одну и ту же дугу, равны.

3)    Если хорды окружности пересекаются, то сумма отрезков одной хорды равна сумме отрезков другой хорды.

8.     Какие утверждения верны?

1)    Если дуга окружности меньше полуокружности или является полуокружностью, то её градусная мера равна градусной мере соответствующего центрального угла.

2)    Если хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

3)    Если вписанный угол опирается на дугу в 30⁰, то центральный угол, опирающийся на ту же дугу равен 15⁰.

9.     Какие из утверждений верны?

1)    Каждая точка биссектрисы неразвёрнутого угла равноудалена от сторон этого угла.

2)    Центр вписанной в треугольник окружности это точка пересечения его медиан.

3)    Если расстояние от точки до центра окружности меньше или равно радиусу окружности, то эта точка лежит на окружности.

10. Какие из утверждений верны?

1)    Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти прямая и окружность пересекаются.

2)    Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

3)    Если вписанный угол равен 60⁰, то центральный угол, опирающийся на ту же дугу окружности, равен 120⁰.

11. Какие из утверждений верны?

1)    Через любые три точки проходит единственная окружность.

2)    Если расстояние между центрами двух окружностей меньше суммы радиусов, то эти окружности пересекаются.

3)    Если дуга окружности составляет 80⁰, то центральный угол, опирающийся на эту дугу, равен 40⁰.

12. Какие утверждения верны?

1)    Центром окружности, описанной около правильного треугольника, является точка пересечения высот.

2)    В равнобедренный треугольник можно вписать окружность.

3)    Если суммы противоположных углов четырёхугольника равна 180⁰, то около него можно описать окружность.

13. Какие утверждения верны?

1)    Если стороны прямоугольника равны 3 и 4, то диаметр описанной около него окружности равен 5.

2)    Около любой трапеции можно описать окружность.

3)    Центром окружности, вписанной в четырёхугольник, является пересечение его диагоналей.

14. Какие из утверждений верны?

1)    Все вписанные углы окружности равны.

2)    Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3)    Если радиусы двух окружностей равны 3и 5, а расстояние между их центрами равно 8, то эти окружности касаются.

15. Какие из утверждений верны?

1)    Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.

2)    Если суммы противоположных сторон четырёхугольника равны, то в этот четырёхугольник можно вписать окружность.

3)    Если основания трапеции равны 4 и 6, то средняя линия этой трапеции равна 10.

4)    В любой четырёхугольник можно вписать не более одной окружности.

16. Какие из утверждений верны?

1)    Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным/

2)    Вписанные углы, опирающиеся на диаметр, прямые.

3)    Около равнобедренной трапеции можно описать окружность.

4)    Каждая точка серединного перпендикуляра равноудалена от концов отрезка.

Критерии оценивания:

 

менее 7 заданий – оценка «2»

8 – 11 заданий – оценка «3»

12 – 14 заданий – оценка «4»

15 – 16  заданий – оценка «5»

Ответы.

1.     23

2.     12

3.     23

4.     12

5.     12

6.     13

7.     2

8.     12

9.     1

10. 23

11. 2

12. 123

13. 1

14. 23

15. 24

16. 234

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ПО

ГЕОМЕТРИИ В 8 КЛАССЕ

Контрольная работа №4 по теме «Окружность».

Вариант I

1. В прямоугольном треугольнике АВС А = 90°, АВ = 20 см; высота АD = 12 см. Найдите АС и cos C.

2. Диагональ  ВD  параллелограмма  АВСD  перпендикулярна  к  стороне  АD.  Найдите  площадь  параллелограмма  АВСD,  если  АВ  =  12  см,
А = 41°.

Вариант II

1. Высота ВD прямоугольного треугольника АВС равна 24 см и отсекает от гипотенузы АС отрезок DС, равный 18 см. Найдите АВ и соs A.

2. Диагональ АС прямоугольника АВСD равна 3 см и составляет со стороной АD угол 37°. Найдите площадь прямоугольника АВСD.

Вариант III
(для более подготовленных учащихся)

1. Диагональ АС равнобедренной трапеции АВСD перпендикулярна к боковой стороне СD. Найдите площадь трапеции, если ее основания равны 10 см и 8 см.

2. Найдите отношение высот BN и AM равнобедренного треугольника АВС, в котором угол при основании ВС равен α.

 

 

 Критерии оценивания:

Оценка «5» - правильное выполнение двух задач; (3 задание на дополнительную оценку)

Оценка «4»  - имеются вычислительные ошибки, с их учетом дальнейшее решение правильное;

Оценка «3»  - решение двух  задач  неполное, есть вычислительные ошибки;

Оценка «2» -  нет решения ни одной задачи.