ФОРМИРОВАНИЕ ПОЗНАВАТЕЛЬНЫХ УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙСТВИЙ В ПРОЦЕССЕ ОРГАНИЗАЦИИ МЕТАПРЕДМЕТНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКАХ МАТЕМАТИКИ

Снигирева Людмила Николаевна магистр по направлению подготовки

 44.04.01 Педагогическое образование  Учитель математики и физики первой квалификационной категории

МКОУ «Лицей №7 имени Шуры Козуб с. Новоивановского» 

Майского муниципального района, КБР

ФОРМИРОВАНИЕ ПОЗНАВАТЕЛЬНЫХ УНИВЕРСАЛЬНЫХ УЧЕБНЫХ ДЕЙСТВИЙ В ПРОЦЕССЕ ОРГАНИЗАЦИИ

МЕТАПРЕДМЕТНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКАХ МАТЕМАТИКИ  

Аннотация: в данной статье рассматривается вопрос развития математических способностей детей через организацию познавательной деятельности на уроках математики путём решения заданий метапредметной направленности. Автор приходит к выводу, что использование метапредметных заданий на уроках математики меняет его структуру, требует новых подходов к контролю и оценке знаний. Отличительной особенностью метапредметной деятельности является то, что учитель развивает   математическое   мышление   учеников на   основе   межпредметных связей, воспитывает самостоятельность в обучении.  Этот метод достаточно эффективен, так как позволяет создать условия для формирования у учащихся навыков овладения  системой  знаний   и способов действий, практических (операционных) умений на основе реальных задач из курса физики.

Ключевые слова: метапредметная деятельность, познавательные УУД, физики, математики, принципа Ферма.

Snigireva Lyudmila Nikolaevna  Master in the field of training 44.04.01 Teacher education Teacher of mathematics and physics of the first qualification category 

MKOU  «Lyceum No. 7 named after Shura Kozub S. Novoivanovsky» Maysky

Municipal district, KBR 

FORMATION OF COGNITIVE UNIVERSAL EDUCATIONAL ACTIONS IN

THE PROCESS OF ORGANIZING META-SUBJECT ACTIVITIES IN MATHEMATICS LESSONS 

Abstract: this article deals with the development of mathematical abilities of children through the organization of cognitive activity in mathematics lessons by solving tasks of meta-subject orientation. The author comes to the conclusion that the use of meta-subject tasks in mathematics lessons changes its structure, requires new approaches to the control and assessment of knowledge. A distinctive feature of metasubject activity is that the teacher develops the mathematical thinking of students on the basis of intersubject connections, educates independence in learning. This method is quite effective, as it allows you to create conditions for the formation of students ' skills of mastering the system of knowledge and methods of action, practical (operational) skills based on real problems from the physics course.

Keywords: metasubject activity, cognitive DMS, physics, mathematics, Fermat's principle.

Каждый учитель знает, что обучать результативно – очень непростая задача. Но как это сделать? Как только этот вопрос встает перед учителем, начинается поиск оптимального пути, эффективных методов и приемов, как из числа традиционных, так и новых. Хотя о последних хочется сказать, что новое в основе своей имеет забытое старое. Конечно, время вносит свои коррективы, заставляет менять акценты в обучении и воспитании, менять свою психологию.

Сейчас, учитывая непростые задачи, которые ставит XXI век, нужно по возможности восстанавливать популярность научной деятельности. Это помогает не только в воспитании индивидуальности, но и сохранить уже во взрослом возрасте детскую способность удивляться таким простым вещам, как падение яблок и лифтов – способность, которая была свойственна Эйнштейну и другим великим физикам-теоретикам. А. Эйнштейн смог выводить сложные уравнения ещё в школьном возрасте, но главное он понимал: «Математика – это, язык, который природа использует для описания своих чудесных тайн...

Воображение важнее знаний» [8]. Позже, когда он стал физиком-теоретиком, успех к нему пришел не из-за его выдающихся мыслительных способностей, а из-за необычайной силы воображения и креативности.

В наше время введение метапредметных компетенций в образовательный процесс, ведёт к  новым способам преподавания предметов, в основе которых лежат познавательные учебные действия. Под познавательными действиями понимают такие, которые обеспечивают познание –  умственный творческий процесс получения и постоянного обновления знаний, необходимых человеку. В психологии познание обозначает способность к умственному восприятию и переработке внешней информации, результатом процесса познавательных действий [1]. В соответствии с деятельностным подходом, действие представляет перечень операций, специально организованных для решения задач определённого типа разной степени обобщённости. Известный российский психолог Н.А. Менчинская отмечала, что действие, усвоенное учащимися в процессе учебно-познавательной деятельности, становится умением [2].

В соответствие с программой формирования УУД, к познавательным действиям (ПУУД) относятся: общеучебные, логические учебные действия и постановка и решение проблем. Их функция – обеспечение успешности усвоения знаний, умений и навыков. Учитель, работающий в современной школе, должен понимать, какие принципиально новые дидактические подходы к уроку регламентирует ФГОС. Весь учебный процесс должен основываться на деятельностном подходе, цель которого – развитие личности учащегося на базе освоения универсальных способов деятельности. Широкие возможности для реализации требований ФГОС даёт организация метапредметной деятельности на уроках математики. Метапредметная деятельность – деятельность за пределами учебного предмета; она направлена на обучение обобщенным способам работы с любым предметным понятием, схемой, моделью и т.д. и связана с жизненными ситуациями. Метапредметность как способ формирования системного мышления обеспечивает формирование целостной картины мира в сознании школьника.

 Ребёнок развивается только при активном восприятии учебного материала, пассивный подход малоэффективен. Именно собственное действие может стать основой формирования будущей самостоятельности ребёнка. Таким образом, образовательная задача состоит в создании условий, провоцирующих детское действие на метапредметном уровне. Методические способы, которыми овладеет учащийся к окончанию обучения в средней школе и должны стать той фундаментальной основой непрерывного образования его в дальнейшем.

Как из предметного материала совершить «прорыв» в метапредметность? 

Современные подходы к обучению: 

•         Традиционный подход – даёт объём знаний

•         Компетентностный подход – даёт возможность использование знаний

•         Системно-деятельнострный подход – Развитие учащихся  плюс методы познания мира.

В работах методистов–математиков, физиков таких как, Боженкова Л.И. [3], Ивашкина Д.А. [4] Хуторской А.В. [7], развито положение о необходимости усложнения характера деятельности учащихся от класса к классу с различными источниками физико-математической информации. Выявлено, что усложнение деятельности учащихся должно идти на основе этапов познания. Так, например, вначале предлагается целенаправленное наблюдение, отбор фактического материала, затем анализ фактов, явлений поиск и объяснение причин отдельных явлений, далее установление межпредметных и причинно-следственных связей между рядом явлений, сравнение, необходимое для обобщающих выводов. Этапы организации познавательных УУД на уроке зависят от характера познавательной деятельности учителя и учащихся,  психологически к которым готов в своём развитии тот или иной класс. Принцип метапредметности позволяет (на уровне вопросов, заданий после параграфа) в содержании математики выделять понятия, утверждения, алгоритмы (правила), методы  рассуждений и  решения  задач (с указанием этапа  формирования) в качестве объектов для дальнейшего исследования в межпредметных и надпредметных (социальной практике) областях (метапонятия, метаявления, метапроцессы). Проектирование исследования учащегося на метапредметном уровне опирается как на его личные интересы, склонности к изучению математики, так и на общекультурный потенциал естественных наук.  Поэтому в условиях реализации образовательной программы среднего общего образования при обучении естественнонаучным предметам, математике существует возможность и в различных формах осуществляться интеграция физического образования в единстве ее подготовительной и образовательной функций, причем есть все основания утверждать, что формирование у подростков ПУУД может нести большой вклад в педагогику физического образования. Физика в школе является основным предметом, где осуществляются разнообразные приложения математики. «Вместе с тем,— пишет известный физик-методист А.А. Пинский в статье «Математическая модель в системе межпредметных связей»,— физика обеспечивает математику практически неограниченным учебным материалом, анализ которого требует разностороннего применения математических методов. Поэтому содержательные связи физики и математики целесообразно трансформировать в межпредметные связи, реализуемые на уроках в методах обучения»[5]. Исходя из чего на уроках  возможно использование следующих средств и форм обучения: межпредметные и метапредметные задания, метапредметный урок (предметный урок и метапредметная тема), межпредметный и метапредметный проекты и т. д.

Для достижения метапредметных образовательных результатов одним из индикаторов может служить  читательская грамотность, в том числе чтение математических текстов – определяется как способность человека понимать и использовать письменные тексты, размышлять о них и заниматься чтением для того, чтобы достигать определённых целей, расширять свои знания и возможности, участвовать в социальной жизни. Поэтому, необходимо находить более разнообразные пути обучения учащихся работе с текстами различного содержания, характера и формата при освоении каждой учебной дисциплины. Следовательно,  учебная информация школьного курса математики должна быть представлена в различных формах и использоваться не только в качестве иллюстраций, но и в виде учебных задач, решение которых предполагает самостоятельную интерпретацию текстов, выдвижение гипотез о его содержании, рефлексию, оценку и др.

Задания для освоения приёмов логического запоминания информации, извлечённой из текстов

Цель: освоение приёмов логического запоминания информации, извлечённой из текстов.

Возраст: 16-17 лет.

Учебные дисциплины: физика, математика.

Форма выполнения задания: работа индивидуальная, в парах и группах.

Описание задания: после чтения и составления плана текста и графических схем учащимся предлагаются следующие варианты выполнения задания:

-                     взаимная проверка по вопросам учебника с опорой на план текста;

-                     пересказ в парах с опорой на план и графическую схему;

-                     составление устной и письменной аннотации с опорой на план и графическую схему;

-                     подготовка учебных докладов с подбором иллюстративного материала.

Критерии оценивания:

•      адекватность и точность воспроизведения текста;

•      адекватность отражения и аннотации основных положений текста;

•      адекватность отражения в графической схеме логических и смысловых связей фрагментов текста.

Рассмотрим работу с текстом математического содержания на примере

задания "Доказательство математических теорем с помощью физических понятий"

Текст [6]

Французский математик П. Ферма в 1660 году сформулировал принцип: из всех возможных путей между двумя точками свет идёт по тому пути, по которому время его прохождения наименьшее.

Из принципа Ферма следует, что в однородной среде свет распространяется прямолинейно: прямая – кратчайшее расстояние между двумя точками, отсюда и время распространение — наименьшее.

Доказательство:

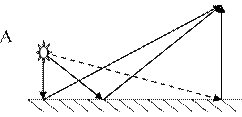
Пусть на зеркальную поверхность ММ падает свет из точки А. Определим путь, по которому свет, отразившись от зеркала, приходит в точку В (рис.1). Из простых геометрических соображений легко выяснить, куда именно должен упасть луч, чтобы время его прохождения по «маршруту» точка А-зеркало-точка В было наименьшим. Проведём из точки В перпендикуляр ВВ₁ к зеркальной поверхности ММ (рис.2). Причём КВ=КВ1. Проведём линию ОВ1. Треугольники ОКВ и ОКВ1 равны друг другу, следовательно ОВ=ОВ1. Поэтому длина пути АОВ равна сумме АО+ОВ, которая будет наименьшей, если точка О лежит на прямой, соединяющей А и В₁.

Наименьшим будет и время прохождения светом этого пути. Если точка падения луча будет находиться левее или правее точки О, то и указанная сумма путей будет больше.

     Рисунок 1                                              _В         Рисунок 2          _В

        М               О                           М     М

Углы наклона лучей АО и ОБ к зеркалу ММ равны друг другу. Однако принято отсчитывать углы не от плоскости зеркала, а от нормали (перпендикуляра) к ней в точке падения. Значит углы α и β равны.

Закон отражения записывается так: α = β. Закон этот, как видно, следствие того, что свет как бы «выбирает» путь, который проходит за наименьшее время.

Из принципа Ферма следует и вторая часть закона отражения: луч падающий, луч отражённый и нормаль к зеркалу в точке падения лежат в одной плоскости.

Из принципа Ферма следует, что падающий и отражённый лучи обратимы. Действительно, если свет будет падать на зеркало от В к О, то он отразится по направлению от точки О к точке А.

Материал: карточки со схемой организации деятельности при доказательстве теорем по Л.И. Боженковой [3].

Схема организации деятельности при доказательстве теорем.

1. Постановка учебной цели;

2)     работа        с        формулировкой   теоремы     и       выявление      средств, необходимых для доказательства теоремы;

3)     соотнесение выявленных средств выполнения УПД с собственными знаниями и умениями;

4)     поиск доказательств теоремы;

5)     составление плана доказательства теоремы;

6)     реализация плана;         

7)     контроль доказательства теоремы;

8)     самооценка результатов выполненной деятельности;

9)     самокоррекция собственных учебных действий при работе с теоремой.

Ожидаемый результат:

1)    доказать принцип Ферма и осознать приёмы, которые для этого использовались;

2)    нужно знать признаки равенства и подобия треугольников, некоторые следствия аксиом стереометрии для доказательства второй части закона отражения лучей, отношение чисел, величин; уметь выполнять действия с дробями и равенствами, выбрать подходящую формулу;

3)    принять решение о помощи;

4)-5) а) вывести следствия из равенства треугольников ОКВ и ОКВ₁; б) вывести следствия из подобия треугольников АМО и ВКО;

в) записать нужные отношения и преобразовать их;

6) Можно воспользоваться приёмами записи доказательства теоремы:

1.                 Вспомнить способы записи решения (Так как А, то В (по И), где И- истинное высказывание: теорема, определение, аксиома, являющиеся обоснованием. а- часть условия, промежуточное условие, В промежуточный вывод, вывод. В, (И- обоснование), так как А. И- обоснование, так как А, то В.

2.                 Выделить в каждом шаге доказательства (решения) промежуточное условие, промежуточный вывод, обоснование.

3.                 Выбрать способ записи решения задачи (доказательства теоремы).

4.                 Реализовать этот способ для каждого шага.

7) нужно воспользоваться соответствующим приёмом:

1.      Проверить правильность записи условия и требования задачи

(теоремы)

2.      Проверить правильность выполнения чертежа

3.      Проверить ход решения, правильно ли использован приём решения

(способ, метод)

4.      Проверить вычисления (если они есть)

5.      Проверить правильность и полноту обоснований

6.      Проверить, рассмотрены ли частные случаи

7.      Проверить проведено ли исследование

8.      Сформулировать идею решения (доказательства)

9.      Перечислить теоретические положения, которые использовались при решении задачи (доказательстве теоремы)

10. Рассказать план решения задачи (доказательства теоремы).

При необходимости воспользуйтесь ответом.

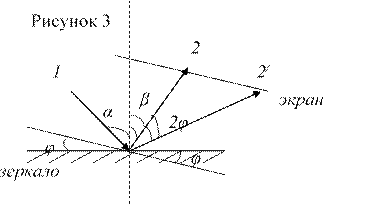
Задание на формирование ПУД и РУД. Организуйте свою учебную деятельность, направленную на доказательство того, что при повороте зеркала на угол φ, угол между падающим и отражённым лучами увеличится на 2φ, используя выше доказательство принципа Ферма.

Главная идея доказательства: при повороте зеркала на угол φ, отраженный луч 2^/ поворачивается относительно луча 2 на угол 2φ. Доказательство, заключается  в том, что повернулась плоскость зеркала на угол φ, а значит и нормаль к зеркалу, и падающий и отражённый луч, которые лежат в одной плоскости, тоже увеличились на φ.  

Всё это на качественном уровне поможет сформировать устойчивый интерес к физико-математическим наукам не на уровне подсознания «сдать ЕГЭ», а на уровне их изучения в дальнейшем, в выборе профессии учеником. Когда ученики с сознанием идут на урок, потому что будет интересно.

Список литературы 

1.     Асмолов А.Г., Бурменская Г.В., Володарская И.А.и др. Формирование УУД в основной школе: от действия к мысли - М. Просвещение,2010.-159с., 9.

2.     Богоявленский Д.Н., Менчинская Н.А. Психология усвоения знаний в школе.М.:Изд-во АПН РСФСР, 1959.-347 с.

3.     Боженкова Л.И. [Электронный ресурс]  Методика формирования универсальных учебных действий при обучении алгебре//[Электронный ресурс]. Код доступа http://avidreaders.ru/download/metodika-formirovaniyauniversalnyh-uchebnyh-deystviy-pri-1.html?f=pdf

4.     Ивашкина Д.А. Эксперимент как метапредметная деятельность: реализация ФГОС на примере курса физики: курс лекций УМП — М.: Педагогический университет "Первое сентября" 2014- 250с

5.     Межпредметные связи естественно-математических дисциплин: пособие для учителей/под ред. В.Н. Федоровой.-М.: Просвещение, 1980.—с.110

6.     Петросян В.Г., Хоконов Х.Б. и др Физика: учебное пособие для 9 кл. общеобразовательных учреждений.- Нальчик, 2000.-194с.: ил. С. 52

7.     Хуторской, А.В. Метапредметный подход в обучении: Научнометодическое пособие / А.В. Хуторской. М. : Эйдос; Изд-во Ин-та образования человека, 2012. – 50 с. (Серия «Новые стандарты»).

8.     Vierevck, 377. См. также: Thomas Friedman, Learning to Keep Learning// New York Times, 13 декабря 2006 г.