Формирование знаково-символических УУД на уроках информатики

 

   Государственное бюджетное образовательное учреждение

 высшего образования Московской области «Академия социального управления»

 

 

Кафедра информационно-коммуникационных технологий

 

 

 

 

 

Практическая работа №4

Система задач в рамках курса информатики, направленная на формирование знаково-символических универсальных учебных действий

по курсу кафедрального инварианта

«Актуальные проблемы развития профессиональной компетентности учителя информатики (в условиях реализации ФГОС ОО)"

 

 

 

 

 

 

 

 

 

 

 

 

 

2022г.

 

 

Система задач в рамках курса информатики, направленная                             на формирование знаково-символических универсальных учебных действий.

Знаково-символические универсальные действия, обеспечивающие конкретные способы преобразования учебного материала, представляют действия моделирования, выполняющие функции отображения учебного материала; выделения существенного; отрыва от конкретных ситуативных значений; формирования обобщенных знаний. Это действия:
- моделирование – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическую или знаково-символическую);
- преобразование модели – изменение модели с целью выявления общих законов, определяющих данную предметную область.

 

Одно из важнейших познавательных универсальных действий - умение решать проблемы или задачи. В основе формирования общего умения решать задачи лежит прием моделирования, который является основным показателем развития знаково-символических универсальных учебных действий. Для успешного обучения в школе должны быть сформированы следующие универсальные учебные действия:

— кодирование/замещение (использование знаков и символов как условных заместителей реальных объектов и предметов);

— декодирование/считывание информации;

— умение использовать наглядные модели (схемы, чертежи, планы), отражающие пространственное расположение предметов или отношения между предметами или их частями для решения задач;

 — умение строить схемы, модели и т. п. 

 

В состав учебного моделирования входят следующие этапы или компоненты:

— предварительный анализ текста задачи;

— перевод текста на знаково-символический язык, который может осуществляться вещественными или графическими средствами;

— построение модели;

— работа с моделью;

 — соотнесение результатов, полученных на модели, с реальностью (с текстами).

Моделирование осуществляется для того, чтобы получить новые данные о реальности или ее описании. Из практики известно, что учащиеся после решения задачи так или иначе проверяют свои ответы для доказательства того, что они удовлетворяют условиям и требованиям задачи.     Принципиа-льно важным при проверке ответов решения задачи является не столько выявление правильности (точности), сколько соотнесение данных, получен-ных на модели, с ее описанием в тексте. При моделировании задачи могут

 

 

быть использованы самые разные знаково-символические средства (отрезки, иконические знаки, графы (простейшие математические модели). 

 

При создании различного типа моделей очень важно определить, какая информация должна быть включена в модель, какие средства (символы, знаки) будут употребляться для каждой выделенной составляющей текста, какие из них должны иметь одинаковую символику, а какие — различную. В процессе построения модели и работы с ней проводится анализ текста и его перевод на математический язык: выделяются известные и неизвестные объекты, величины, отношения между ними, основные и промежуточные вопросы.

     Один из подходов к моделированию при решении задач предложен Ж. Верньё. Для анализа текста задачи он использовал следующие две категории: состояния объекта и трансформации. Под состояниями объекта понимается описание в тексте задачи тех ситуаций, в которых действует объект. Различают начальное, конечное и промежуточное состояния (или ситуации). Трансформации — это те изменения в объектах (или с объектами), которые происходят при переходе их от одного состояния к другому. Трансформация приводит к новому типу отношений между состояниями объекта. В схемах, предложенных Ж. Верньё, для анализа и решения задач данные обозначаются в виде геометрических фигур: объекты — квадраты; отношения между сос-тояниями объектов — линии, стрелки, на которых указывают направленность отношений; отношения между величинами состояния объекта — круги. Заданные числовые значения величин объекта и отношений между величи-нами указываются соответствующими числами, знак при которых фиксирует характер отношения величин (разностное, кратное, равенство, целое/часть). 

 

Наряду с описанными выше способами также используется табличный способ представления содержания задачи. Он чаще всего применяется для задач с разнородными величинами, когда часть из них является перемен-ными, связываемыми постоянной величиной. Это, как правило, задачи на «процессы». При создании таблицы фактически реализуются те же этапы учебного моделирования.

 

Разработать систему задач в рамках курса информатики я постараюсь  используя  тему  «Алгоритмы»:

 

В 5 -7 классах по курсу «Информатика и ИКТ» мы знакомим учащихся с понятием «Алгоритм», способами записи алгоритмов и с видами алгоритмов.

Учитель объясняет детям, что каждый человек в повседневной жизни, во время учебы или на работе решает огромное количество задач. Одни из них  мы решаем автоматически не задумываясь, а другие требуют усилий для поиска их решения, чтобы достичь поставленную цель.

 

 

Задача №1  Алгоритм «Посадка деревьев». Составить словесный алгоритм и блок-схему.

                               

 

                                 Решение:

 

Словесный алгоритм	Блок-схема
1.     Выкопать ямку в земле; 2.     Опустить в ямку саженец; 3.     Засыпать ямку с саженцем землей; 4.     Полить саженец водой.

 

Таких задач в школьной или повседневной жизни можно придумать много: «Вычислить периметр прямоугольника при известных его сторонах а и в», «Вычислить площадь квадрата при  известной его стороне а», «Найти НОД двух натуральных чисел», «Поездка в театр», «Сдача экзамена» и т.п.

 

При этом для одной и  той  же задачу можно составить как линейный так и разветвленный, и циклический алгоритмы.

 

Задача №2: Алгоритм « Выполнить последовательность действий нахождения значения следующего выражения:

(5,88+5,52)-2,8:(5*0,103-0,015)».

Составить словесный алгоритм и блок-схему.

 

 

Во многих задачах бывает заранее известно правило, по которому следует осуществлять преобразование входной информации в выходную. Это правило может быть  представлено в идее формулы или подобного плана действий. Рассмотрим некоторые математические задачи:

 

b

Задача №3  «Вычислить периметр прямоугольника, если известно, что его длина больше ширины в 2 раза». Можно помочь себе рисунком:

                                                                 а > b в 2 раза

 

	a

 

Решение:

 

 

Словесный алгоритм	Блок-схема
1.Ввести сторону а; 2. Вычислить сторону в через а; 3. Вычислить периметр прямоуголь-ника; 4. Вывести периметр прямоугольника.

 

Аналогичные задачи: «Вычислить площадь прямоугольника, если известно, что ширина меньше  его длины на 3 см.», «Вычислить периметр прямоугольного треугольника, если известны его катеты а и b» и т.п.

 

Задача №4  В треугольнике АВС АВ=15см, ВС на 3 см меньше АВ, АС в 3 раза меньше АВ. Чему равен периметр треугольника АВС?

Решение:

Периметр треугольника равен сумме длин всех сторон: Р=АВ+ВС+АС. Найдем ВС=15-3=12 (см), АС=15:3=5 (см). Вычисляем Р = 12+15+5=32(см).

 

Можно схематично показать решение этой задачи:

 

 

 

                                                                                                                            

 

 

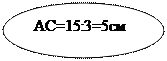
Таким образом, в результате преобразования исходных данных по известным нам правилам (изученным ранее) мы получили новую информацию о том, чему равен периметр треугольника.

 

 

Задача №5  Исполнитель Вычислитель умеет выполнять только две команды:

                            - умножить на 2;

                            - прибавить один.

Составьте для Вычислителя наиболее короткую программу получения из числа 1 число 50.

Эту задачу можно решать схематично или с помощью таблицы:

 

Команда	Результат
Взять число 1 Умножить на 2 Прибавь 1 Умножить на 2 Умножить на 2 Умножить на 2 Прибавь один Умножить на 2	1 1*2=2 2+1=3 3*2=6 6*2=12 12*2=24 24+1=25 25*2=50

 

 

 

 

 

 

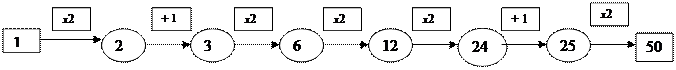
Аналогичная задача только с другими командами: Исполнитель Вычислитель забыл одну из старых команд, но зато усвоил новую команду и теперь его СКИ имеет вид:

                - умножить на 2;

                - стереть последнюю букву.

Составьте для Вычислителя наиболее короткую программу получения из числа 68 числа 136 и 6.

Эту задачу также можно решать схематично или с помощью таблицы.

 

Можно предложить учащимся простейшие задача следующего содержания:

 

Задача №6  Придумайте пример линейного алгоритма, который можно записать с помощью следующей блок-схемы:

  

 

 

 

 

 

 

 

 

 

 

Такие задания можно придумать и на алгоритм с ветвлением, и на циклический алгоритм.

 

       Одним из подходов к моделированию можно рассмотреть «Решение логических задач с помощью таблиц». Переход от текстовой формы представления информации к табличной часто помогает решать достаточно трудные задачи. С помощью таблиц удобно фиксировать наличие или отсутствие связей между объектами.

 

Задача №7   В одном доме живут Воронов, Павлов, Журавлев, Синицын. Один из них математик, другой художник, третий писатель, а четвертый – баянист. Известно, что:

1)    Ни Воронов, ни Журавлев не умеют играть на баяне;

2)    Журавлев не знаком с Вороновым;

3)    Писатель и художник уезжают на дачу к Павлову;

4)    Писатель собирается написать очерк о Синицыне и о Воронове.

Требуется определить, кто есть кто.

 

	Воронов	Павлов	Журавлев	Синицын
Математик
Художник
Писатель
Баянист

 

Надо помнить, что при заполнении таблицы «0» и «1» каждая ячейка должна быть заполнена так, чтобы в одной строке и в одном столбце может записана только одна «1», а все остальные «0».

Аналогично заполняются такие таблицы «+» и « - ».

 

При изучении темы «Программирование» учащиеся сталкиваются со следующими заданиями:

 

Задача №8   Построить блок-схему по программе, записанной на языке  Паскаль:

 

var

    x,y: real;

     begin

       writeln (‘введите x=’);

       readln (x);

       if x<=10 then y:=210 else y:= x*x*x;

       writeln (‘при  x=’, x, ‘y=’ y)

       end.

 

 

 

 

 

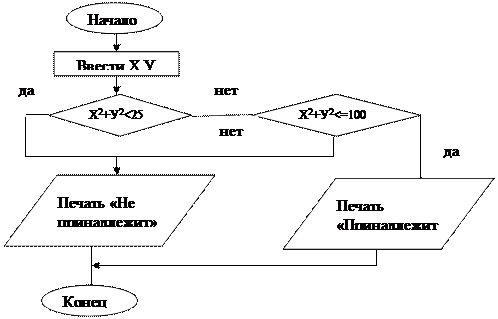
Задача №9  Дана блок-схема. Написать программу по блок-схеме:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

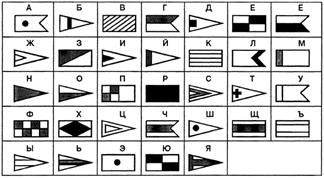
К этой же теме можно добавить множество заданий по кодированию информации (азбука Морзе, флажковая азбука и т.п.) из рабочей тетради

Л. Босовой.

Именно тексты, представленные на естественных языках (русском, английском и т. д.), чаще всего подвергаются кодированию. Существуют три основных способа кодирования текста:

1)    графический — с помощью специальных рисунков или значков;

 

 

2)    символьный — с помощью символов того же алфавита, что и исходный текст (шифр Цезаря);

 

3)   

числовой – с помощью чисел.

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й
1	2	3	4	5	6	7	8	9	10	11
К	Л	М	Н	О	П	Р	С	Т	У	Ф
12	13	14	15	16	17	18	19	20	21	22
Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
23	24	25	26	27	28	29	30	31	32	33

 

 

В настоящее время обработкой текстовой информации всё чаще занимается компьютер. При вводе в память компьютера текстовой информации осуществляется ее двоичное кодирование.

 

Присвоение символу конкретного кода — это вопрос соглашения, которое фиксируется в кодовой таблице. Кодовая таблица — это пред­ставление символов в компьютере. Во всем мире в качестве стандарта принята таблица ASCII.

 

 

 

 

 

 

 

http://www.uchportal.ru/publ/24-1-0-2079 при решении текстовых задач

 

http://edu.convdocs.org/docs/28/index-6921.html?page=5 знаково-символьные УУД

Скачано с www.znanio.ru