Формулы приведения.

Формулы приведения.

Цель. Вывести формулы приведения, заполнив таблицу. Записать правило по формулам приведения. Научиться использовать формулы приведения при решении примеров.

Решим пример: cos (-405°)= cos (405°)=cos (360°+45°) =

cos 45°=.

В этом примере  использовали понятие четности и нечетности и периодичность.

 Как найти, например, cos  150°, представив в виде тригонометрической функции острого угла?

Для этого служат формулы приведения, которые дают возможность тригонометрические функции любого угла, больше 90°, преобразовать к тригонометрическим функциям острого угла.

Любой угол на тригонометрическом круге можно представить двумя способами: отложить его от горизонтального или от вертикального диаметра.

Например, 150° = 90° + 60° ( от вертикального)  или

150° = 180° - 30° ( от горизонтального). Результат получится одинаковый.

cos 150°=cos(90° + 60°) = - sin 60°=.

cos 150°=cos(180° - 30°) = - cos 30°=.

Выведем формулы приведения, заполним таблицу и установим правило. Для вывода каждой формулы используется соответствующая формула из теорем сложения. Например, для вывода формулы cos ( ) используется формулы cos (

Учащимся предлагается начертить в тетради таблицу, содержащую 10 строк и 6 столбцов. Образец демонстрируется на экран с помощью проектора.

Каждому ученику дается карточка, например ,  В 3   или  А 6    

Учащиеся выводят формулы и заполняют таблицу.

Установим и запишем правило.

Решение примеров у доски с использованием выведенного правила.

Пример 1.  Вычислить √3sin 300°.

√3sin 300°= √3sin  ( 270°+30°) = -√3cos   30°= -√3 ˔= -1,5

Пример 2.  Вычислить cos .

cos  = cos ( π -  = - cos - 0,5

Пример 3.  Вычислить  - sin( 3α –π) - cos( 3α -   при α =  .

- sin( 3α –π) + cos( 3α +  = + sin(π- 3α) - cos(   = sin3α + sin3α =

2 sin3α = 2 ˔ sin3˔  = 2 ˔ sin  =2 ˔  = 1.

Пример 4.  Вычислить

 =  =

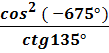
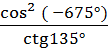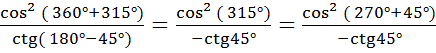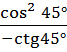= =  = - 0,5 .

Домашнее задание выдается на индивидуальных карточках.