Функции. Область определения и множество значений; график функции. Построение графиков функций, заданных различными способами.

Лекция № 9

Тема: Функции. Область определения и множество значений; график функции. Построение графиков функций, заданных различными способами.

Количество часов: 2 часа

Цель: расширение понятийной базы по теме «Функция» за счет включения в нее новых элементов; формирование у обучающихся способностей к самостоятельному построению новых способов действия на основе метода рефлексивной самоорганизации.

План:

1.       Понятие функции. Область определения и множество значений.

2.       Построение основных графиков функций.

Вопрос 1. Понятие функции. Область определения и множество значений.

Одним из основных объектов изучения в дисциплине «Математика» являются функции.

С их помощью могут быть сформулированы как законы природы, так и разнообразные процессы, происходящие в технике. Отсюда – объективная важность математического анализа как средства изучения функций.

Определение. Если каждому элементу х множества становится в соответствие вполне определенный элемент у множества , то говорят, что на множестве Х задана функция у = f(x).

При этом х называется независимой переменной (или аргументом), у – зависимой переменной, а буква f обозначает закон соответствия.

Множество Х называется областью определения (или существования) функции, а множество Y – областью значений функции.

Функции делятся на два класса:

1.                 явные;

2.                 неявные

Определение. Функция называется  явной, если она задана формулой, в которой правая часть не содержит зависимой переменной.

Определение. Функция у аргумента х называется неявной, если она задана уравнением F(x, y) = 0, не разрешенным относительно зависимой переменной.

Из основных функций новые функции могут быть получены двумя способами при помощи:

ü алгебраических действий;

ü операций образования сложной функции.

При работе с любой функцией мы предъявляем ей стандартный набор вопросов. И первый, самый важный вопрос – это область определения функции. Иногда эту область называют множеством допустимых значений аргумента, областью задания функции и т.п.

Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Область определения любой функции устанавливают:

1. Математика. Это законы и правила, которые всегда должны выполняться. Эти правила не зависят от нашего желания и вида задания. Они работают всегда. Область определения по этим правилам иногда называют "естественной".

2. Люди. Это дополнительные ограничения на область определения функции, которые могут быть (а могут и не быть) в любом конкретном задании и зависят исключительно от составителя задания.

Как найти область определения функции?

Итак, нам надо найти все допустимые значения икса для какой-то конкретной функции. Самый широкий набор значений, как правило - это все действительные числа от -∞ до +∞.

В математике работают в два этапа.

На первом этапе ищем в функции операции, которые могут оказаться недопустимыми при каких-то значениях икса. Т.е. ищем потенциально опасные операции.

На втором этапе определяем иксы, которые не приводят к запретному действию в этих самых операциях. Это и будет область определения функции.

Что такое потенциально опасные операции? Это операции, в которых существуют принципиальные ограничения.

До 9-го класса включительно:

1. Деление. Нельзя делить на ноль.

2. Извлечение корня. Нельзя извлекать корни чётной степени из отрицательных чисел.

В выпускных классах и ВУЗах:

3. Логарифмы. Ограничения в логарифмах: если log_ab = c, то а>0, a≠1, b>0.

4. Тригонометрия. Ограничения в тригонометрии: значения углов, для которых тангенс и котангенс не существуют, ограничения на выражения под знаком арксинуса, арккосинуса.

Пример 1. Найти область определения функции:

у = 3x - 2

Первый этап. Ищем в этой функции потенциально опасные операции.

Деление есть? Деления нет. Корни? Корней нет. Логарифмы? Нет их. И тригонометрии тоже нет. В этой функции не может получиться никаких запретных действий.

Какой бы икс мы не взяли. Этих действий в функции просто не содержится. Значит, ответ: х - любое число. Записывается ответ так:

D(f)=(-∞;+∞)

D(f) - это обозначение области определения функции.

Как видите, в этом примере второй этап вовсе не понадобился. Бывает.

Пример 2. Найти область определения функции:

у = 1/x

Ищем потенциально опасные операции. Такая операция есть. Деление.

Определяем иксы, которые не приводят к запретному действию, т.е. делению на ноль. Собственно, к делению на ноль приводит лишь одно значение икса: x=0. Следовательно, все остальные значения безопасны. Областью определения функции будут все действительные числа, кроме нуля. В краткой записи:

Запись очень похожа на запись ответа для неравенств, правда? Всё верно. И там и здесь - запись промежутков числовой оси.

Пример 3. Найти область определения функции:

Выполняем первый этап: осматриваем функцию, на предмет потенциально опасных операций.

Внимание! Мы ничего не решаем! Не упрощаем, не складываем дроби, не раскладываем на множители, не извлекаем корни. Мы «осматриваем» функцию. Любые преобразования могут изменить область определения функции и мы получим неверный ответ.

Сразу же выполняем и второй этап: то, что найдём в процессе осмотра, будем записывать, чтобы не забыть.

Итак, в первом слагаемом видим квадратный корень из выражения с иксом. Это потенциально опасная операция. Под корнем, при каких-то иксах, может оказаться отрицательное число. Обезопасим себя вот такой записью (второй этап):

x² - 8x + 12 ≥ 0

Квадратный корень извлекается только из положительных чисел и нуля. Всё подкоренное выражение должно быть больше, либо равно нулю. Не икс, а всё подкоренное выражение, целиком.

В этом же слагаемом есть деление на 3. Игнорируем. Тройка - не икс, нулём стать не может.

Второе слагаемое. В нём есть деление на выражение с иксом. Знаменатель не может быть равен нулю. Записываем (второй этап):

х - 3 ≠ 0

В третьем слагаемом опять есть деление. Записываем:

х+1 ≠ 0

Теперь сводим все наши записи в систему неравенств:

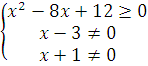
Система необходима, так как все наши условия должны выполняться одновременно.

Осталось решить эту систему. В ответе получится область определения этой функции.

Ответ:

Множество значений функции. Пусть задана функция у = f(x) с областью определения D(f). Множество чисел, пробегаемое функцией у, когда х принимает все возможные значения (т.е. при всех значениях ), называется множеством значений функции, или областью значений функции, или областью изменения функции и обозначается через E(f).

Пример 1. Найти множество значений функции:

у = 2х² + 5.

Решение

Поскольку об области определения функции ничего не сказано, мы должны рассматривать её на естественной области определения, т.е. при всех действительных значениях х (). Поскольку в области определения , причём все неотрицательные значения выражение 2х² принимает, данная функция, очевидно, принимает все значения, не меньшие, чем число 5:  .

Ответ: E(f) = [5; +∞).

Пример 2. Найти область значений функции у = 2х² + 5 на отрезке [-2; 5].

Решение

На этот раз область определения задана явно, используем это. Самое трудное здесь – «уследить», что при  выражение х² изменяется от 0 до 25 (это становится очевидным, если, например, нарисовать график функции у = х²; можно получить это и аналитически, если рассмотреть отдельно, как меняется выражение х² на отрезках, где оно монотонно – [–2; 0] и [0; 5], на первом из них это выражение убывает, а на втором – возрастает; это хорошо видно на том же графике). После этого легко получаем:

.

Ответ: E(f) = [5; 55].

Пример 3. Найти область изменения функции у = 2х² + 5 на отрезке [2; 5].

Решение

Рассуждая аналогично и учитывая, что на этот раз функция в области определения монотонна (возрастает), получаем:
.

Ответ: E(f) = [13; 55].

Вопрос 2. Построение основных графиков функций.

Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Элементарные функции делятся на:

1.           алгебраические – функции, в которых над аргументом проводится конечное число алгебраических действий;

2.           неалгебраические (трансцендентные) – всякие неалгебраические функции

Знание основных элементарных функций, их свойств и графиков не менее важно, чем знание таблицы умножения. Они как фундамент, на них все основано, из них все строится и к ним все сводится.

Основными элементарными функциями являются:

- постоянная функция (константа),

- корень n – ой степени,

- степенная функция,

- показательная функция,

- логарифмическая функция,

- тригонометрические и обратные тригонометрические функции.

Вопросы для самопроверки:

1.     Дайте определение функции.

2.     Что такое «область определения функции» и «множество значений функции»?

Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:

1.      Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.  Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни  – М.: Просвещение, 2022. – 431 с.: ил.

2.      Выгодский М.Я. Справочник по элементарной математике / М.Я. Выгодский. – М: Книга по требованию, 2013.-513с.

3.      Материалы по математике Материалы в Единой коллекции цифровых образовательных ресурсов: http://school_collection.edu.ru/collection/matematika/

4.      Вся элементарная математика: Средняя математическая интернет – школа http://www.bymath.net

5.      http://www.cleverstudents.ru/

Скачано с www.znanio.ru