Функции y=xn , их свойства и графики.

Конспект урока по теме: Функции y=xⁿ , их свойства и графики.

Цели:

Образовательная -   ввести понятие степенной функции с натуральными показателями; рассмотреть свойства  функции ; рассмотреть свойства функции

Развивающая - формирование способности анализировать, обобщать полученные знания; формирование логического мышления.

Воспитательная -  активизировать интерес к получению новых знаний; воспитание графической культуры, формирование точности и аккуратности при выполнении чертежей; формирование умений работать в группе.

Задачи:

Образовательные:

• построить определение степенной функции с натуральным показателем;
• формировать способность к построению графиков функций у = х²ⁿ и у = х²ⁿ⁺¹;
• тренировать способности к чтению графиков построенных функций;
• формировать умения устанавливать свойства функций по графикам;

Развивающие:

• развивать умения обобщения и систематизации при актуализации знаний по видам функций;
• развивать умения анализировать и делать выводы в ходе исследования функций;
• развивать коммуникативные умения и навыки при работе в группах по исследованию функций и при представлении своих результатов;
• развивать исследовательскую компетентность при работе в группах по исследованию функций;
• развивать рефлексивные умения и навыки;

Воспитательные:

• формировать умения и навыки самоорганизации и самореализации при выполнении и исследовании функций;
• формировать этические нормы общения у учащихся при групповой работе.

Планируемые результаты:

В ходе урока учащиеся развивают умения

·                                 систематизировать знания о графиках функций, их свойствах;

·                                 устанавливать соответствие между графиком и формулой;

·                                 делать обобщения и выводы.

Методы, используемые на уроке: наглядный, иллюстративный, исследовательский, творческий.

Формы организации урока: коллективная, групповая, индивидуальная работа.

Этапы урока:

- самоопределение к деятельности (1 минута)

- актуализация знаний (7 минут),

- постановка учебной задачи (2 минуты),

- открытие нового знания (14 минут),

- первичное закрепление (6 минут),

- самостоятельная работа (7 минут),

-творческая работа (5 минут),

- рефлексия (2 минута)

- домашнее задание (1 минута).

Тип урока: урок изучения нового материала.

Оборудование: проектор, компьютер.

Ход урока:

I.       Организационный момент

II.    Актуализация знаний (подготовка учащихся к восприятию нового материала). Презентация    Запишем тему в тетрадь.

Каковы цели нашего урока? (познакомиться со степенной функцией и её свойствами)

III.Изучение нового материала

Определение: Функцию вида у=xⁿ, где n= 1, 2, 4, 5, …., называют степенной функцией с натуральным показателем.

Какие степенные функции вы уже знаете? (y=x, y= x², y=x³).

Назовите формулы других степенных функций.

Начиная с n = 3, мы о функции y= xⁿ пока ничего не знаем. Наша цель выяснить, как выглядят графики этих функции и какими свойствами они обладают.

На какие две группы можно разделить  показатели степенных функций (четные и нечетные)? Класс делится на две группы:

1 группа:  в MSOfficeExel чертит и исследует функции y= x², y=x⁴, y= x⁶.

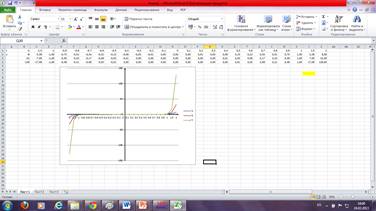
2 группа: в MSOfficeExel чертит и исследует функции y= x³, y=x⁵, y= x⁷.

Составим таблицы значений для  этих функций и особенно внимательно посмотрим, как ведут себя функции на отрезке [-1;1].

Перед учащимися ставится задача ответить на следующие вопросы:

·         Чем похожи и чем отличаются графики функций.

·         Перечислить свойства функций.

·         В ходе работы оформить опорный конспект.

·          

1 группа (результат работы)

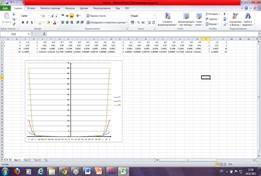
2 группа (результат работы)

После окончания работы один представитель от группы представляет результат работы (сопровождается презентацией).

Учащиеся другой группы заполняют конспект.

Рассмотреть построение графика

IV. Закрепление:

№Решение упражнений
145, 138, 155(а)

Дом. работа
№139, 136, 146,155(в) + тест для подготовки к ОГЭ.

V.    Подведение итогов.

Какая функция называется степенной?

Как выглядит график степенной функции с натуральным четным показателем, нечетным показателем?

Перечислите свойства изученных степенных функций.

Опорный конспект

Степенная функция

с натуральным показателем

Приложение(тест)

1. На рисунке изображён график квадратичной функции y = f(x).

Какие из следующих утверждений о данной функции неверны? Запишите их номера.

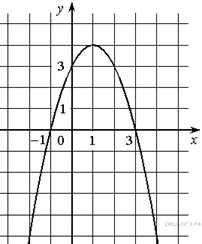
1) f(−1) = f(3).

2) Наибольшее значение функции равно 3.

3) f(x)>0 при −1<x<3.

2. Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А) 

Б) 

B) 

ГРАФИКИ

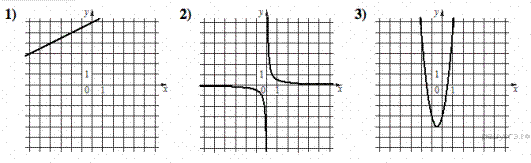
В таблице под каждой буквой укажите соответствующий номер.

3. На рисунке изображены графики функций вида y = ax²​ + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.

КОЭФФИЦИЕНТЫ

А) 

Б) 

В) 

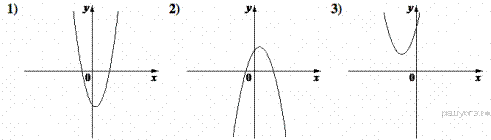
В таблице под каждой буквой укажите соответствующий номер.

4. На рисунках изображены графики функций вида . Установите соответ­ствие между знаками коэффициентов  и  и графиками функций.

КОЭФФИЦИЕНТЫ

А) 

Б) 

В)  

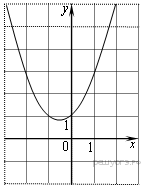
5. Найдите значение  по графику функции , изображенному на рисунке.

Скачано с www.znanio.ru