Геометрический смысл производной. Алгебра и начала анализа 10 класс.

Применение производной  Геометрический смысл производной.

Краткая теория.

Геометрический смысл  производной связан с углом наклона касательной, проведенной  к графику функции в данной точке или с угловым коэффициентом наклона касательной.

( Теория и разобранные примеры должны быть записаны в тетрадь)

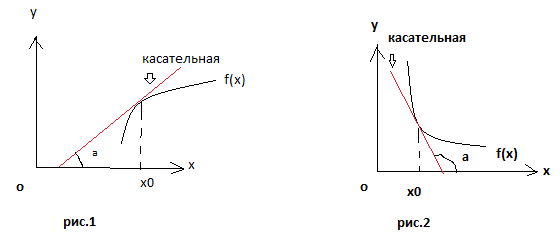
На рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а на рис.2 этот угол тупой. Если угол наклона  касательной острый, то функция при увеличении значения переменной Х  будет возрастать.  Если  угол наклона касательной тупой, как на рис.2, то функция на этом участке убывает.

Геометрический смысл производной:

Пример1.  Вычислить тангенс угла наклона касательной к графику функции  y= x  - x³    в точке с абсциссой  Х₀ = - 2.         Решение.   

    f ´(x) = tg ɑ    y ´ = (x – x³)´=  1 – 3x²          y ´( - 2)= 1 - 3·(-2)² = 1 – 12= - 11. Ответ: -11.

Пример2.  Найти угловой коэффициент наклона касательной, проведенной к графику функции f(x) = 2Sin x + 3Cos x  в точке х_{0 = π /2 .      Решение.}

   f ´(x) = K      f ´ (x) =(2Sin x + 3Cos x )´ = 2Cos x – 3Sin x

f ´ ( _{π /2}) =( 2Cos ( _{π /2) – 3Sin( π /2) = 2·0 - 3·1 = -3.}         Ответ. -3

Пример3.  Найти угол наклона касательной  к графику функции    y= - tg x, проходящую  через точку   М (π ; 0).           Решение.   

   f ´(x) = tg ɑ        tg ɑ = y´ (х) = (- tg x )´ = - 1/ (Cos² x )          из точки  М (π ; 0)  координата  x₀  = π (вторая координата не используется) подставим в найденную производную вместо  х число π, тогда получим :

 tg ɑ = -1 / Cos² π.      Cos π = -1 (таблица значений тригонометрических функций).

  tg ɑ = -1 / ( -1)² = -1/1 = -1   угол ɑ = 135°  (таблица значений тригонометрических функций. Угол наклона касательной может быть в пределах  0° < ɑ <180° ).     Ответ: 135.

Пример4.   На рисунке изображен график функции и касательные , проведенные к нему в точках с абсциссами A, B, C, D.

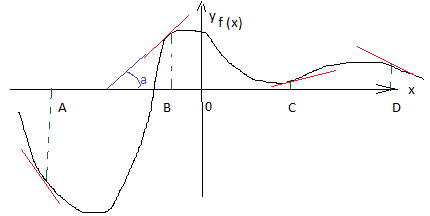В правом столбце указаны значения производной функции в точках A, B, C, D.Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

При решении  заполните таблицу, расчерченную ниже, в которой для каждой точки  укажите номер соответствующего значения производной.

(При записи ответа укажите  полученное четырехзначное число).

Решение.

Пояснения к решению. Их можно в решении не писать только заполненную таблицу и ответ.(Пояснения даны для того, чтобы вы поняли, как решать такого типа задание).

Сначала  определим знаки производной в каждой отмеченной  точке. Для этого надо мысленно продолжить каждую касательную ( красная) до пересечения с осью ОХ ( как сделано синим цветом для точки B). Увидим, что  в точке A угол наклона касательной будет тупой ( угол берем только с положительным направлением оси ОХ, куда указывает стрелка оси), в точке B этот угол острый, в точке С – острый, в точке D – тупой. Производная  f ´(x) = tg ɑ         Значение производной в заданной точке равно тангенсу угла наклона касательной, проведенной в заданной точке  Для острых углов тангенс положительный, чем больше острый угол тем больше его тангенс. Для тупых углов тангенс отрицательный, чем больше тупой угол тем меньше значение его тангенса.                                                                                                                                                        В точках  B и С производная положительная, причем в т.B острый угол больше , чем в   т. С. Значит, в таблицу ответов  под точкой B  пишем цифру 3, под точкой С пишем цифру 4.                 В точках  A  и D производная отрицательна, причем в т. А тупой угол больше, чем в т.D.                В таблице ответов под точкой А  пишем цифру1, под точкой D пишем цифру 2.                

                                                                           Ответ:    1342

Самостоятельная работа.

Задача 1.    Найти угловой коэффициент наклона касательной, проведенной к графику функции

y(x)=5 x  +3 x²   в точке с абсциссой  Х₀ = 3.     

Задача 2.     Вычислить тангенс угла наклона касательной к графику функции  

f(x) =7x² + 0,5 Sin x,  проходящую через точку с координатами  N (0 ; 8). 

Задача 3.    Найти угол наклона касательной  к графику функции    y= - Ctg x,  проходящую  через точку   D (π /2 ; 10).   

Задача 4.   На рисунке изображен график функции и касательные , проведенные к нему в точках с абсциссами A, B, C, D.

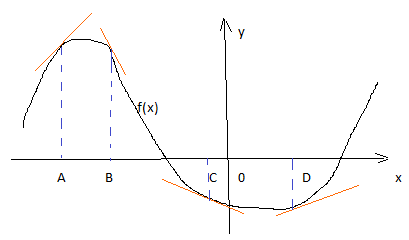В правом столбце указаны значения производной функции в точках A, B, C, D.Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

При решении  заполните таблицу, расчерченную ниже, в которой для каждой точки  укажите номер соответствующего значения производной.

(При записи ответа укажите полученное четырехзначное число).

Задание 5.  Найти в учебнике по алгебре и выписать формулу уравнения касательной  к графику функции и записать назначение всех величин, входящих в эту формулу.

Ответы на задачи.

Задача 1.    23

Задача2.    0,5

Задача 3.    45

Задача 4.    2314   

Задача 5.    y = y₀ +f´(x₀)·( x – x₀),   где  y_{0  -} значение функции в точке x_0,          

f´(x₀) - значение  производной функции в точке x_0, 

_{Х    -} переменная, x₀   - заданное по условию значение переменной.