Геометрический смысл производной, касательная. Наибольшее и наименьшее значение функций

Геометрический смысл производной, касательная Наибольшее и наименьшее значение функций

 

Вариант 1

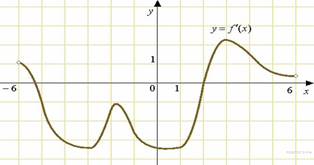
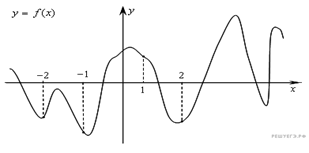
1. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле . Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

2. Най­ди­те точку мак­си­му­ма функ­ции .

 

3. Най­ди­те наи­боль­шее зна­че­ние функции  на от­рез­ке .

 

4. Най­ди­те точку мак­си­му­ма функ­ции .

 

5. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

 

6. Най­ди­те точку мак­си­му­ма функ­ции

.

7. Най­ди­те точку ми­ни­му­ма функ­ции .

 

8. 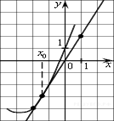На ри­сун­ке изоб­ражён гра­фик функ­ции y=f(x) и ка­са­тель­ная к нему в точке с абс­цис­сой x₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции f(x) в точке x₀.

 

 

 

 

Вариант 2

 

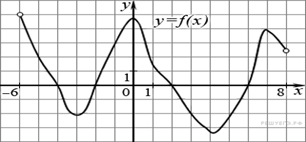
1. На ри­сун­ке изоб­ра­жен гра­фик функ­ции y = f(x), опре­де­лен­ной на ин­тер­ва­ле
 (−6; 8). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции по­ло­жи­тель­на.

 

2. Най­ди­те точку ми­ни­му­ма функ­ции .

     

3. Най­ди­те наи­мень­шее зна­че­ние функ­ции на от­рез­ке .

4. Най­ди­те точку мак­си­му­ма функ­ции .

 

5. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

6. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

 

7. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

 

8. 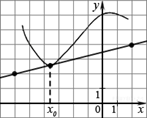На ри­сун­ке изоб­ражён гра­фик функ­ции y=f(x) и ка­са­тель­ная к нему в точке с абс­цис­сой x₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции f(x) в точке x₀.

 

 

 

 

 

 

 

Вариант 3

 

1. 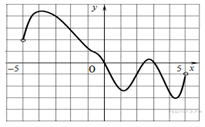На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−5; 5). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции  от­ри­ца­тель­на.

 

2. Най­ди­те наи­мень­шее зна­че­ние функ­ции .

 

3. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

4. Най­ди­те точку ми­ни­му­ма функ­ции .

 

5. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

6. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

 

7. Най­ди­те точку мак­си­му­ма функ­ции 

 

 

8. .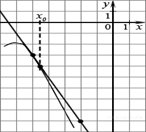На ри­сун­ке изоб­ражён гра­фик функ­ции y=f(x) и ка­са­тель­ная к нему в точке с абс­цис­сой x₀. Най­ди­те зна­че­ние про­из­вод­ной функ­цииf(x) в точке x₀.

 

 

Вариант 4

 

1. На ри­сун­ке изоб­ражён гра­фик y=f'(x) — про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (-8; 3). В какой точке от­рез­ка [-3; 2 ] функ­ция f(x) при­ни­ма­ет наи­боль­шее зна­че­ние?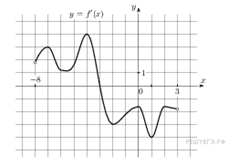

2. Най­ди­те наи­боль­шее зна­че­ние функ­ции .

 

3. Най­ди­те наи­мень­шее зна­че­ние функ­ции на от­рез­ке .

4. Най­ди­те точку ми­ни­му­ма функ­ции .

 

5. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

6. Най­ди­те точку мак­си­му­ма функ­ции .

 

7. Най­ди­те точку ми­ни­му­ма функ­ции .

 

 

8. На ри­сун­ке изоб­ражён гра­фик функ­ции y=f(x) и ка­са­тель­ная к нему в точке с абс­цис­сой x₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции f(x) в точке x₀.

 

 

 

 

 

 

 

Вариант 5

 

 1. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 14). Най­ди­те ко­ли­че­ство точек мак­си­му­ма функ­ции f(x) на от­рез­ке [−6; 9]. 

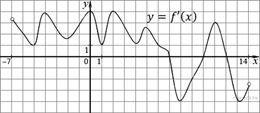
2. Най­ди­те точку мак­си­му­ма функ­ции .

3. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

4. Най­ди­те точку мак­си­му­ма функ­ции .

 

5. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

6. Най­ди­те точку ми­ни­му­ма функ­ции .

7. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

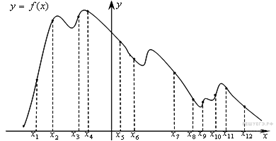
8. На ри­сун­ке изоб­ражён гра­фик функ­ции  и две­на­дцать точек на оси абс­цисс: , , , , . В сколь­ких из этих точек про­из­вод­ная функ­ции  от­ри­ца­тель­на?

 

 

 

 

 

 

 

 

Вариант 6

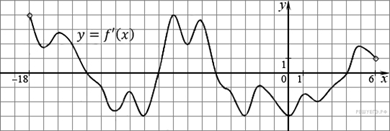
1. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−18; 6). Най­ди­те ко­ли­че­ство точек ми­ни­му­ма функ­ции f(x) на от­рез­ке [−13;1].

2. Най­ди­те точку ми­ни­му­ма функ­ции 
3. Найди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

4. Най­ди­те точку мак­си­му­ма функ­ции .

 

5. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .
6. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

7. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

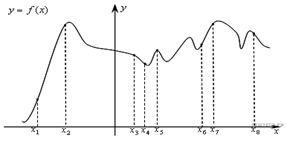
8. На ри­сун­ке изоб­ражён гра­фик функ­ции  и во­семь точек на оси абс­цисс: , , , , . В сколь­ких из этих точек про­из­вод­ная функ­ции  по­ло­жи­тель­на?

 

 

 

 

 

Вариант 7

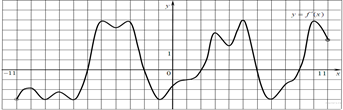
1. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−11; 11). Най­ди­те ко­ли­че­ство точек экс­тре­му­ма функ­ции f(x) на от­рез­ке [−10; 10].

2. Най­ди­те наи­мень­шее зна­че­ние функ­ции 

3. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке 
4. Най­ди­те точку ми­ни­му­ма функ­ции .

5. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .
6. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

7. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .
8. На ри­сун­ке изоб­ражён гра­фик функ­ции  и ка­са­тель­ная к нему

в точке с абс­цис­сой Х₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции

 в точке Х₀.

 

 

 

Вариант 8

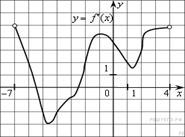
1. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 4). Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции f(x). В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

 

2. Най­ди­те наи­боль­шее зна­че­ние функ­ции 

3. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .
4. Най­ди­те точку мак­си­му­ма функ­ции 

5. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .
6. Най­ди­те точку мак­си­му­ма функ­ции .

 

7. Най­ди­те точку мак­си­му­ма функ­ции .

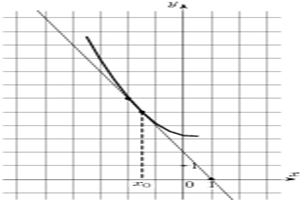
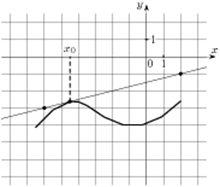
8. На ри­сун­ке изоб­ражён гра­фик функ­ции  и ка­са­тель­ная к нему

в точке с абс­цис­сой Х₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции

 в точке Х₀.

 

 

 

Вариант 9

1. 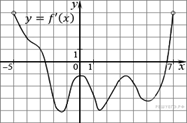На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−5; 7). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции f(x). В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

 2. Най­ди­те точку мак­си­му­ма функ­ции .

3. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

4. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .
5. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .
6. Най­ди­те точку ми­ни­му­ма функ­ции .

7. Най­ди­те точку ми­ни­му­ма функ­ции .

8. На ри­сун­ке изоб­ражён гра­фик функ­ции  и ка­са­тель­ная к нему

в точке с абс­цис­сой Х₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции

 в точке Х₀. 

 

 

Вариант 10

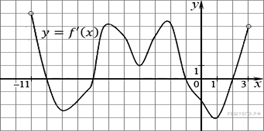
1. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−11; 3). Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции f(x). В от­ве­те ука­жи­те длину наи­боль­ше­го из них.

 

2. Най­ди­те наи­мень­шее зна­че­ние функ­ции .

 3. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

4. Най­ди­те точку ми­ни­му­ма функ­ции , при­над­ле­жа­щую про­ме­жут­ку .

5. Най­ди­те точку мак­си­му­ма функ­ции .

 

6. Най­ди­те точку мак­си­му­ма функ­ции

.

7. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

8. На ри­сун­ке изоб­ражён гра­фик функ­ции  и ка­са­тель­ная к нему

в точке с абс­цис­сой Х₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции

 в точке Х₀.

 

 

 

 

Вариант 11

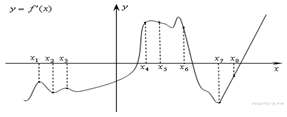
1. На ри­сун­ке изоб­ражён гра­фик  - про­из­вод­ной функ­ции f(x).На оси абс­цисс от­ме­че­ны во­семь точек: x₁, x₂, x₃, ..., x₈. Сколь­ко из этих точек лежит на про­ме­жут­ках воз­рас­та­ния функ­цииf(x) ? 

2. Най­ди­те наи­боль­шее зна­че­ние функ­ции . 

 3. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

4. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

5. Най­ди­те точку ми­ни­му­ма функ­ции .
6. Най­ди­те точку ми­ни­му­ма функ­ции .

7. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .
8. На ри­сун­ке изоб­ражён гра­фик функ­ции  и ка­са­тель­ная к нему в точке с абс­цис­сой . Най­ди­те зна­че­ние про­из­вод­ной функ­ции в точке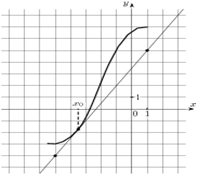 

 

 

 

 

Вариант 12

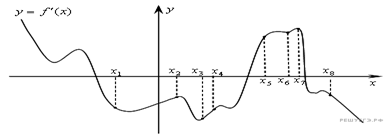
1. На ри­сун­ке изоб­ражён гра­фик  про­из­вод­ной функ­ции  и во­семь точек на оси абс­цисс:    ,. В сколь­ких из этих точек функ­ция  убы­ва­ет?

 

2. Най­ди­те точку ми­ни­му­ма функ­ции .

 

3. Най­ди­те наи­боль­шее зна­че­ние функ­ции  на от­рез­ке .

4. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

5. Най­ди­те наи­мень­шее зна­че­ние функ­ции  на от­рез­ке .

6. Най­ди­те точку мак­си­му­ма функ­ции 

7. Най­ди­те точку мак­си­му­ма функ­ции .

8. На ри­сун­ке изоб­ра­жен гра­фик функ­ции  и от­ме­че­ны точки −2, −1, 1, 2. В какой из этих точек зна­че­ние про­из­вод­ной наи­боль­шее? В от­ве­те ука­жи­те эту точку.

 

 

 

 

 

 

 

 

 

 

 

№ задания   вариант	1	2	3	4	5	6	7	8
1	14	-2	12	-4,5	1	-7	4	2
2	4	3	9	-4	-24	10	-54	0,25
3	7	2	5	-2	36	-10	0	-2
4	-3	3	16	-6	-4	-4	2	-0,25
5	1	3	9	-6	10	5	6	7
6	1	-1	-14	1	0	12	-2	4
7	5	16	32	1	4	-6	0	-2
8	-3	9	15	-5	0	-17	-1	0,25
9	18	1	-16,5	-5	4	1	1	-0,25
10	6	2	5	0,5	2	-7	3	0,25
11	3	4	6	3	-3	-1	3	1,5
12	5	3	11	-6	-1	17	-4	-2

 

 

Скачано с www.znanio.ru