Геометрия и Алгебра 7 класс

Геометрия в 7 классе. Геометрия в задачах ОГЭ, ЕГЭ и олимпиад

Задача 1.

Два равносторонних треугольника ABC и CDE имеют общую вершину (см. рисунок). Найдите угол (в градусах) между прямыми AD и BE (углом между двумя пересекающимися прямыми называется наименьших из углов, образованных при пересечении)

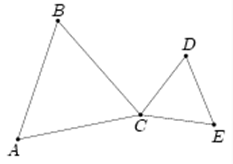
Решение задачи

Заметим, что треугольники ACD и BCE равны по первому признаку. Действительно, AC=BC, CD=CE и ∠DCA=60∘+∠BCD=∠ECA.  Значит, ∠CAD=∠CBE. Тогда 

∠BPA=180∘−∠ABP−∠PAB=180∘−(60∘+∠CBE)−(60∘−∠CAD)=60

.

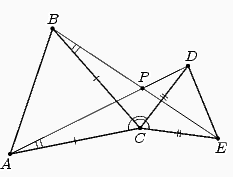
Приведем набросок альтернативного рассуждения, которое тоже может быть оформлено в строгое решение (для этого см. тему "Движения плоскости"). Заметим, что при повороте вокруг точки C на 60 градусов точка E перейдет в точку D, а точка B перейдет в точку A. Значит, отрезок BE перейдет в отрезок AD. Потому и угол между ними равен 60 градусам. 

Задача 2.

На основании AB равнобедренного треугольника ABC взята точка E, и в треугольники ACE и ECB вписаны окружности (касаются сторон треугольников ACE и ECB), касающиеся отрезка CE в точках M и N. Найдите длину отрезка MN, если AE=1и BE=3. 

Решение задачи

Обозначим через K и L точки касания окружности, вписанной в треугольник EBCсо сторонами EB и BC, соответственно.  
Тогда заметим, что EC+EB−BC=EN+NC+EK+KB−CL−LB=EN+EK= поскольку CL=CN, BL=BK и EK=EN. Значит, EN=12(EC+EB−BC). Рассуждая аналогично, получаем, что EM=12(EA+EC−AC) Поэтому

MN=|EN−EM|=12|EC+EB−BC−EA−EC+AC|=12|EB−EA|=1.

Здесь третье равенство следует из того, что AC=BCAC=BC по условию.

Задача 3.

Условие

Угол при вершине A треугольника ABC равен 120^o. Окружность касается стороны BC и продолжений сторон AB и AC. Докажите, что расстояние от вершины A до центра окружности равно периметру треугольника ABC.

Подсказка

Пусть D — точка касания окружности с прямой AB. Докажите, что отрезок AD равен полупериметру треугольника ABC.

Решение

Пусть O — центр окружности, D, E и F — точки касания с прямыми AB, BC и AC соответственно, 2p — периметр треугольника ABC. Тогда AD = AF, BE = BD и CE = CF. Поэтому

2p = AB + BC + AC = AB + (BE + EC) + AC =

= (AB + BE) + (EC + AC) = (AB + BD) + (CF + AC) = AD + AF.

Значит, AD = AF = p.

Поскольку луч AO — биссектриса угла DAC, то DAO = 60^o. Из прямоугольного треугольника ADO находим, что

AO = 2AD = 2p.

Задача 4.

На сторонах AB, BC и CA равностороннего треугольника  ABC  взяты точки C1, A1 и B1соответственно, причем так, что B1C1⊥AC,  A1C1⊥AB,  B1A1⊥BC. Найдите A1B:A1C.

Решение задачи

Заметим, что все углы треугольника A1B1C1 равны по 60∘, так как ∠BA1C1=90∘−∠ABC=30∘, а ∠B1A1C1=180∘−∠BA1C1−∠B1A1C=60∘. Остальные углы вычисляются аналогично.

Следовательно, треугольник A1B1C1 равносторонний, откуда получаем, что △AC1B1=△BA1C1=△CB1A1 по катету (B1C1=C1A1=A1B1) и острому углу  

(∠A=∠B=∠C=60∘).

Остается заметить, что поскольку ∠BA1C1=30∘, катет напротив этого угла вдвое меньше гипотенузы, то есть A1B=2BC1 причем BC1=CA1 ввиду равенства указанных выше трех прямоугольных треугольников. Отсюда следует, что A1B=2A1C.

Задача 5.

В треугольнике ABC проведены биссектрисы AD и BE. Известно, что DE – биссектриса угла ADC. Найдите градусную величину угла A.

Проведём через вершину B прямую, параллельную AD, до пересечения с прямой AC в точке G. Заметим, что  ∠GBA = ∠BAD = ∠DAE = ∠BGC,  то есть треугольник BAG равнобедренный  (AB = AG).  Как известно, биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. Применяя это свойство к биссектрисам DE и BE, получим  DA : DC = AE : EC = BA : BC.  Но  DA : DC = BG : BC  (треугольники ACD и GCB подобны). Значит,  BA = BG  и треугольник BAG – равносторонний. Поэтому  ∠BAG = 60°.

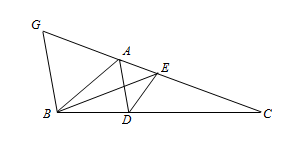
Задача 6.

Тимофей резал бумажный треугольник на кусочки (все разрезы - прямые). Сначала он разрезал этот треугольник на две части. Потом разрезал на два куска одну из полученных частей, и так далее. Когда ему надоело резать, оказалось, что общее количество углов у всех получившихся фигур равно 2015. Какое наименьшее количество разрезов мог сделать Тимофей? 

Решение задачи

При разрезании выпуклого многоугольника прямым разрезом получаются два многоугольника. При этом могут образоваться не более четырех новых углов, то есть, суммарное количество углов в образовавшихся многоугольниках превышает количество углов первоначального многоугольника не более, чем на 4. Поскольку 2015=3+503⋅4, то Тимофею хватит 503 разреза (а меньшего количества разрезов не хватило бы). Пример для 503 разрезов: достаточно каждый раз разрезать треугольник на треугольник и четырехугольник.

Задача 7.

Какое наибольшее число сторон может иметь многоугольник, являющийся пересечением четырехугольника и треугольника?

Решение задачи

Ответ: 8.

Пример, когда в пересечении треугольника и четырехугольника получается восьмиугольник, см. ниже на картинке.

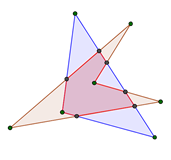
Оценка. Докажем, что в пересечении не может образоваться многоугольник с 9 или больше сторонами. Заметим, что каждая сторона треугольника не может пересекать внутренность четырехугольника больше двух раз (т.е. на стороне треугольника не может быть больше двух непересекающихся «участков», которые лежат внутри четырехугольника), в этом несложно убедиться перебором случаев (два раза сторона треугольника может пересекать внутренность четырехугольника, см. на картинке выше на самую длинную сторону). Аналогично, каждая сторона четырехугольника может пересекать внутренность треугольника не более одного раза (в этом тоже можно убедить простым перебором). Тогда для того, чтобы у пересечения треугольника и четырехугольника было по крайней мере 9 сторон, необходимо, чтобы две стороны треугольника пересекали внутренность четырехугольника два раза. Но нетрудно убедиться, что такое невозможно (тоже перебор случаев, ниже есть рисунок одной из возможных ситуаций), т.к. в этом случае в пересечении треугольника и четырехугольника будут получаться два многоугольника. Т.е. наибольшее число сторон у многоугольника, который образовался в пересечении треугольника и четырехугольника, равно 8.

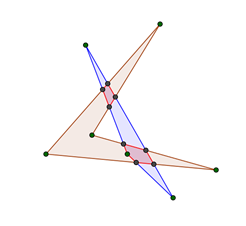
Замечание 1. Если бы в условии задачи было сказано, что четырехугольник должен быть выпуклым, то ответ был бы равен 7.

Замечание 2. В 2013 году один из преподавателей центра онлайн-обучения «Фоксфорд» (а именно Кожевников Павел Александрович) опубликовал научную статью, в которой он доказал следующую теорему.

ТЕОРЕМА.

Если пересечение двух многоугольников (n1n1-угольника и n2n2-угольника) — многоугольник, то число сторон в нем не более

k=2n1+2n2−6−max{[|n1−n2|2]−1,0}.

При этом существуют такие n1-угольник и n2-угольник, что их пересечением будет k-угольник. 

Здесь [x]— целая часть числа x, т.е. наибольшее целое число, которое не превосходит xx. Например, [5,3]=5,[−0,5]=−1,[7]=7.

Доказательство данной теоремы достаточно непростое. Поэтому мы не будем разбирать его здесь. Но мы можем убедиться, что в статье получена точно такая же оценка как и в предложенном решении, поскольку в нашем случае (n1=3n1=3, n2=4n2=4):

k=2n1+2n2−6−max{[|n1−n2|2]−1,0}=6+8−6−max{−1,0}=8.