
График прямой пропорциональности
Цели: определить график прямой пропорциональности как прямую, проходящую через начало координат; выявить расположение прямой в зависимости от знака коэффициента пропорциональности; формировать умение строить график прямой пропорциональности по формуле и выполнять обратное действие – записывать по графику формулу функции.
Ход урока
I. Устная работа.
1. Найдите область определения функции.
а) y = 3x + 2; б) y = ![]() ; в) y
=
; в) y
= 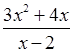 ;г)
y =
;г)
y = ![]() ; д) y =
; д) y = ![]() x; е) y
= 2x2 + 6x + 1.
x; е) y
= 2x2 + 6x + 1.
2. Является ли функция прямой пропорциональностью:
а) y = 182x;б) y = ![]() ;в) y =
;в) y = ![]() x;г)
y = –17x2; д) y =
x;г)
y = –17x2; д) y = ![]() ; е) y
= 3x + 11?
; е) y
= 3x + 11?
3. Функция задана формулой у = kх. Найдите коэффициент прямой пропорциональности k, если:
а) х = 2; у = 4; б) x = ![]() ; y =
–4;в) х = 3; у =
; y =
–4;в) х = 3; у = ![]() ; г) х = 0; у = 0.
; г) х = 0; у = 0.
II. Объяснение нового материала.
Начинаем с рассмотрения конкретной функции (см. учебник, с. 66). Можно предложить учащимся лабораторную работу: подобрать функции, заданные формулами:
у = 0,5х; у = –0,5х;
у = х; у = –х;
у = 1,5х; у = –1,5х;
у = 2х; у = –2х;
у = 2,5х; у = –2,5х;
у = 3х; у = –3х;
у = 3,5х; у = –3,5х;
у = 4х; у = –4х.
Затем заполнить таблицу значений функции при –4 ≤ х ≤ 4 с шагом 0,5.
выводы:
1) График прямой пропорциональности является прямой, проходящей через начало координат.
2) Если коэффициент пропорциональности k > 0, то график расположен в первой и третьей координатных четвертях.
3) Если коэффициент пропорциональности k < 0, то график расположен во второй и четвертой координатных четвертях.
На основе этих выводов учащиеся выводят простейший алгоритм построения графика прямой пропорциональности:
1-й шаг. Для х1 0 вычислить у1 по формуле у = kх.
2-й шаг. Отметить в координатной плоскости точки с координатами (0; 0) и (х1; у1).
3-й шаг. Провести прямую через построенные точки.
III. Формирование умений и навыков.
Упражнения, выполняемые на этом уроке, направлены на отработку алгоритма построения графика прямой пропорциональности и нахождения значений функции по графику.
1. № 300, № 302.
№ 302.
|
Решение: у = –0,5х |
|
Пусть х = 3, тогда у = –0,5 · 3 = –1,5. Проведем прямую, проходящую через начало координат и точку с координатами (3; –1,5).
а) Если х = –2, то у = 1; б) у = –1 при х = 2;
если х = 4, то у = –2; у = 0 при х = 0;
если х = 1, то у = –0,5. у = 2,5 при х = –5.
Если у = –150, то найдем х, решив уравнение:
–0,5х = –150;
х = –150 : (–0,5);
х = 300.
При выполнении этого задания повторяем с учащимися правило нахождения по графику значения функции по данному значению аргумента и наоборот (отмечаем точку на оси абсцисс; проводим прямую, перпендикулярную оси абсцисс, до пересечения с графиком функции; из полученной точки опускаем перпендикуляр на ось ординат и находим соответствующее числовое значение ординаты).
Также на этом примере показываем, что очень важен выбор правильной величины единичного отрезка. Если взять в качестве единицы измерения одну клеточку, то будет очень неудобно строить график, точки будут «слипаться», чертеж будет грязным и нефункциональным.
При больших значениях аргумента или функции (у = –150) удобнее работать с формулой и выполнять действия аналитически (решить уравнение; вычислить по формуле).
2. № 303 (устно).
Выполняем работу по предыдущему чертежу.
3. № 305, № 306.
|
№ 305. Решение: а) у = 1,7х; б) у = –3,1х; в) у = 0,9х; г) у = –2,3х; д) у = kх, где k > 0; е) у = kх, где k < 0. |
|
После выполнения этого задания обсудить с учащимися, почему график а) расположен в первой четверти выше графика в).
№ 306. Решение:
Все графики являются прямыми, проходящими через начало координат, значит, функции являются прямыми пропорциональностями и их можно задать формулой у = kх. Задача сводится к нахождению коэффициента k.
Выберем на каждом графике произвольную точку с целыми координатами:
I (2; 6), значит, 6 = k · 2; k = 3; у = 3х;
II (4; 1), значит, 1 = k · 4; k = 0,25; у = 0,25х;
III (2; –2), значит, –2 = k · 2; k = –1; у = –х;
IV (2; –6), значит, –6 = k · 2; k = –3; у = –3х.
Ответ: у = 3х; у = 0,25х; у = –х; у = –3х.
IV. Проверочная работа.
Вариант 1
1. График функции у = kх проходит через точку В (–30; 3). Найдите k.
2. Построить графики функций:
а) у = 5х; б) у = –5х.
В каждом случае указать координаты двух точек графика, лежащих выше оси абсцисс.
Вариант 2
1. График функции у = kх проходит через точку А (4; –80). Найдите k.
2. Построить графики функций:
а) у = 6х; б) у = –6х.
В каждом случае указать координаты двух точек графика, лежащих ниже оси абсцисс.
V. Итоги урока.
Домашнее задание: 1. № 301; № 304. № 357.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.