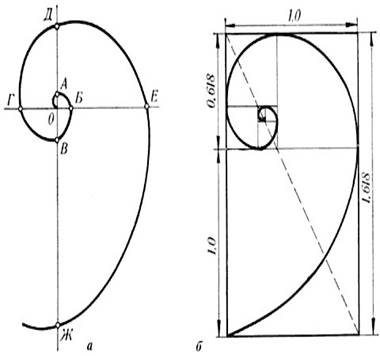
Спираль Архимеда

Форма спирально завитой раковины привлекла внимание Архимеда.

Он изучал ее и вывел уравнение кривой: r =       aφ,    где    a        –        некоторое фиксированное         число.         Эту    кривую стали называть спиралью Архимеда. Геометрическим       свойством, характеризующим спираль Архимеда, является постоянство расстояний между соседними витками. Каждое из них равно 2πа. Действительно, если угол увеличивается на 2π, т. е. точка делает один оборот против часовой стрелки, то радиус увеличивается на 2πа, что и составляет расстояние      между соседними витками.

Применение архимедовой спирали в

древности

Архимедову спираль использовали как наилучший способ определения площади круга. С ее помощью был улучшен древний греческий метод нахождения площади круга через измерение длины окружности. Спираль дала возможность более точного измерения длины окружности, а следовательно, и площади круга. Однако вскоре, когда Архимед попытался вычислить более точно значение , которое упрощало нахождение площади круга, было доказано, что спираль для этого не подходит.

Спирали в реальной жизни

Гете – поэт, естествоиспытатель и художник подчеркивал тенденцию природы к спиральности: паук плетет паутину спиралеобразно, спирально закручивается ураган, молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».

Спираль Архимеда в настоящее время широко

используется в технике. Самая распространенная его разновидность - винтовой ротор в обычной мясорубке. Примером применения в технике архимедовой спирали также является самоцентрирующийся патрон. Данный механизм используется в швейных машинках для равномерного наматывания ниток. Ныне спираль Архимеда заслуживает особого внимания при обучении компьютерной графике.

Живопись и спираль Архимеда

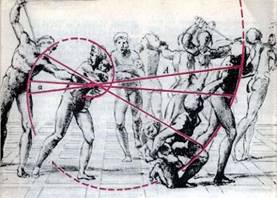
 Многофигурная композиция выполнена Рафаэлем в 1509-1510          гг.      На подготовительном        эскизе проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается ... спираль! Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован эскиза и создал гравюру "Избиение младенцев".

неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого

Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции "Избиение младенцев" или только "чувствовал" ее. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел. Об этом свидетельствуют добавленные им новые элементы композиции, подчеркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста,

идущая от головы женщины, - в левой части композиции и лежащее тело ребенка - в ее центре.