Индивидуальное задание 14

Индивидуальное задание 14

1.           

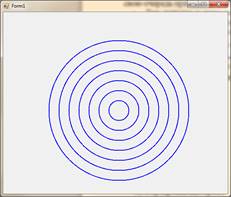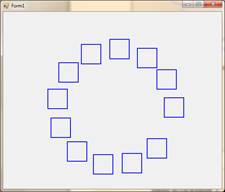
2.            Напишите приложение, которое строит ряд квадратов. Центр квадратов совпадает с центром экрана. Число квадратов задается при первом вызове рекурсивного метода.

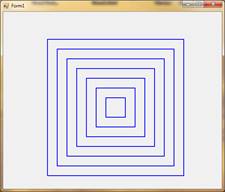
3.           

4.           

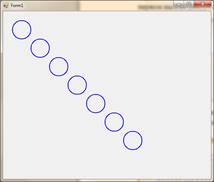
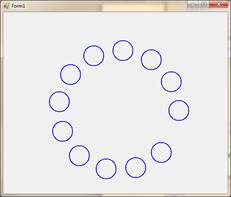
5.            Напишите приложение, которое строит ряд окружностей, цен- тры которых лежат на окружности. Число окружностей задается при первом вызове рекурсивного метода.

6.           

7.           

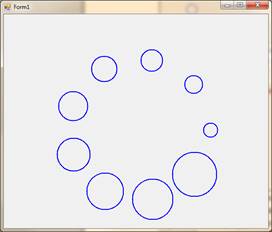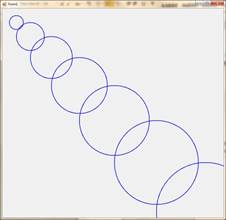
8.            Напишите приложение, которое строит ряд увеличивающихся окружностей, центры которых лежат на спирали. Число окружностей задается при первом вызове рекурсивного метода.

9.            Вычислить, используя рекурсию, выражение:

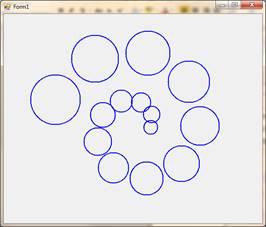
10.        Напишите приложение, которое строит ряд окружностей. Чис- ло окружностей удваивается на каждом шаге (в рекурсивном методе происходит два рекурсивных вызова). Центры окружностей выбираются каждый раз произвольно (случайно). Линии связывают центры окруж- ностей «предка» и «порожденных» от нее. Число рекурсий задается при первом вызове рекурсивного метода.

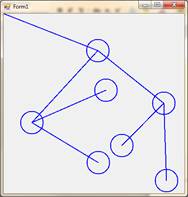
11.       

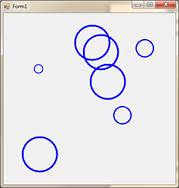12.        Напишите приложение, которое строит ряд уменьшающихся окружностей. Число окружностей удваивается на каждом шаге (в рекур- сивном методе происходит два рекурсивных вызова). Число рекурсий задается при первом вызове рекурсивного метода.

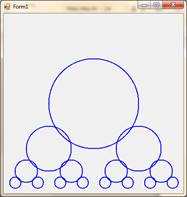
13.       

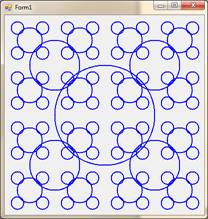14.        Постройте ковер Серпинского.

15.        Разработайте программу построения треугольника Серпинско-

го.

16.        Реализуйте программу визуализации построения первых n ша- гов множества Кантора.

17.        Реализуйте рекурсивный алгоритм вычисления n-го числа Фибоначчи.

18.        Реализуйте рекурсивный алгоритм вычисления n-го факториа-

ла.

19.        Реализуйте рекурсивный подсчет суммы всех элементов мас-

сива. Сумма элементов массива считается по следующему алгоритму: массив делится пополам, подсчитываются и складываются суммы эле- ментов в каждой половине. Сумма элементов в половине массива под- считывается по тому же алгоритму, то есть снова путем деления попо- лам. Деления происходят, пока в получившихся кусках массива не ока- жется по одному элементу и вычисление суммы, соответственно, не станет тривиальным.

20.        Дана монотонная последовательность, в которой каждое нату- ральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, ... По данному натуральному n выведите первые n членов этой последова- тельности.