Индивидуальные задания 8

Индивидуальные задания 8

1.            Дана матрица A(3,4). Найти наименьший элемент в каждой строке матрицы. Вывести исходную матрицу и результаты вычислений.

2.            Дана матрица A(3,3). Вычислить сумму второй строки и про- изведение первого столбца. Вывести исходную матрицу и результаты вычислений.

3.            Вычислить сумму S элементов главной диагонали матрицы B(10,10). Если S>10, то исходную матрицу преобразовать по формуле b_ij=b_ij+13.5; если S£10, то b_ij=b_ij²-1.5. Вывести сумму S и преобразованную матрицу.

4.            Дана матрица F(15,15). Вывести номер и среднее арифметическое элементов строки, начинающейся с 1. Если такой строки нет, то вывести сообщение «Строки нет».

5.            Дана матрица F(7,7). Найти наименьший элемент в каждом столбце. Вывести матрицу и найденные элементы.

6.            Найти наибольший элемент главной диагонали матрицы A(15,15) и вывести всю строку, в которой он находится.

7.            Найти наибольшие элементы каждой строки матрицы Z(16,16) и поместить их на главную диагональ. Вывести полученную матрицу.

8.            Найти наибольший элемент матрицы A(10,10) и записать нули в ту строку и столбец, где он находится. Вывести наибольший элемент, исходную и полученную матрицу.

9.            Дана матрица R(9,9). Найти наименьший элемент в каждой строке и записать его на место первого элемента строки. Вывести исходную и полученную матрицы.

10.        Вычислить количество H положительных элементов последнего столбца матрицы X(5,5). Если H<3, то вывести все положительные элементы матрицы, если H³3, то вывести сумму элементов главной диагонали матрицы.

11.        Вычислить и вывести сумму элементов матрицы A(12,12), расположенных над главной диагональю матрицы.

12.        Найти номер столбца матрицы, в котором находится наименьшее количество положительных элементов.

13.        Дан двухмерный массив 20x20 целочисленных элементов. Найдите все локальные максимумы. (Элемент является локальным мак- симумом, если он не имеет соседей, больших, чем он сам).

14.        Дана матрица 7x7. Найти наибольший элемент среди стоящих на главной и побочной диагоналях и поменять его местами с элементом, стоящим на пересечении этих диагоналей.

15.        Задана матрица, содержащая N строк и M столбцов. Седловой точкой этой матрицы назовем элемент, который одновременно является минимумом в своей строке и максимумом в своем столбце. Найдите ко- личество седловых точек заданной матрицы.

16.        Дана квадратная матрица 10x10. Реализуйте программу для транспонирования матрицы по главной и побочной диагонали.

17.       

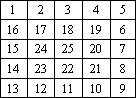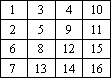
18.        Требуется заполнить змейкой квадратную матрицу так, как показано на рисунке: заполнение происходит с единицы из левого верх- него угла и заканчивается в правом нижнем числом N², где N – порядок матрицы. Реализуйте программу для матрицы 10x10.

19.        Дана шахматная доска (матрица 8x8). Разработать программу, показывающую последовательность ходов конем с произвольной клет- ки. Конь ходит в соответствии с шахматными правилами, но в произ- вольную сторону (сгенерировать случайным образом). В клетку, с кото- рой начинается ход, выводится единица. В клетку, в которую идет далее конь, записывается двойка и т. д. Ходить конем на клетки, на которых уже побывал конь, нельзя. Алгоритм останавливает работу, когда конем ходить некуда. Максимальная последовательность ходов – 64.

20.        Проверка на симпатичность. Рассмотрим таблицу, содержа- щую n строк и m столбцов, в каждой клетке которой расположен ноль или единица. Назовем такую таблицу симпатичной, если в ней нет ни