ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПОВЫШЕННОЙ СЛОЖНОСТИ

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПОВЫШЕННОЙ СЛОЖНОСТИ

Для решения геометрических задач повышенной сложности необ- ходимо:

1.            знать, как представляются на плоскости такие геометрические объекты, как точка, прямая, отрезок и окружность;

2.            уметь находить уравнение прямой, соединяющей две заданные точки;

3.            уметь определять координаты точки пересечения двух пря- мых;

4.            знать, как провести перпендикуляр к прямой или определить, являются ли прямые параллельными;

5.            уметь находить скалярное и векторное произведение;

6.            находить площадь многоугольника;

7.            уметь работать с фигурами на плоскости.

Напомним основные моменты, связанные с этими понятиями.

Каждую точку плоскости можно считать вектором с началом в точке (0,0). Обозначим через a=(x, y) вектор с координатами (x, y). Дли-

на вектора (его модуль) вычисляется по формуле

a =                 .

Скалярное произведение двух векторов – это число, равное про- изведению модулей этих векторов на косинус угла между ними, (a,b)=|a|

∙   |b| ∙ cos φ. Если вектор a имеет координаты (x₁, y₁), а вектор b коорди- наты – (x₂, y₂), то скалярное произведение вычисляется по формуле (a,b)= x₁ ∙ x₂ + y₁ ∙ y₂.

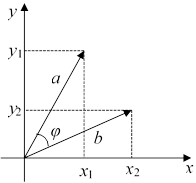
Рис. 16.1. Иллюстрация к скалярному произведению векторов

Заметим, что если угол φ острый, то скалярное произведение (a,b)>0, если угол φ тупой, то (a,b)<0. Если два вектора перпендикуляр- ны, то их скалярное произведение равно нулю.

Векторным произведением двух векторов a и b называется век- тор [a × b], такой, что

·               длина его равна |[a × b]|=|a| ∙ |b| ∙ sin φ;

·               вектор [a × b] перпендикулярен векторам a и b;

·               вектор [a × b] направлен так, что из его конца кратчайший по- ворот от a к b виден происходящим против часовой стрелки.

Длина векторного произведения равна площади параллелограмма, построенного на векторах a и b.

Через координаты векторов a и b векторное произведение выра- жается следующим образом:

где i, j, k – единичные вектора осей Ox, Oy, Oz соответственно. При решении задач на плоскости координаты z₁ и z₂ равны нулю.

В этом случае [a × b]=(x₁ ∙ y₂ – x₂ ∙ y₁)∙ k.

Если вектор a образует с осью Ох угол α, а вектор b – угол β, то для скалярного произведения справедлива формула [a × b]=(|a| ∙ |b| ∙ sin(β-α))∙ k. Это означает, что для ненулевых векторов векторное произ- ведение равно нулю тогда и только тогда, когда векторы параллельны. Если поворот от вектора а к вектору b по наименьшему углу выполня- ется против часовой стрелки, то [a × b]>0, если по часовой стрелке, то [a × b]<0.

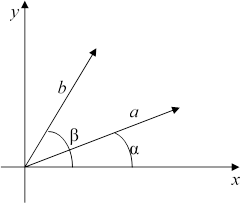
Рис. 16.2. Иллюстрация к векторному произведению

Рассмотрим задачи, при решении которых используются скаляр- ное и векторное произведения.

Задача 1. «Штраф за левые повороты» [1]. В городе Х водите- лям запрещено выполнять левые повороты. За каждый такой поворот водитель должен уплатить штраф в размере М рублей. Для слежки за водителями в городе установлена компьютерная система, фиксирую- щая координаты автомобиля в начале движения, в конце движения и во время поворота.

Исходные данные: N – количество зафиксированных координат автомобиля, (x_i, y_i) – координаты автомобиля в процессе движения, i=1,2, …, N, где (x₁, y₁) – точка начала движения, (x_N, y_N) – последняя точка маршрута автомобиля.

Требуется по заданной последовательности координат движения вычислить сумму штрафа водителя.

(xi+1, yi+1)

(x_i, y_i)

(xi-1, yi-1)

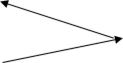
Рис. 16.3. Иллюстрация к задаче «Штраф за левые повороты»

Траекторию движения автомобиля можно представить в виде ло- маной, состоящей из направленных отрезков из точек (x_i, y_i) в точки (x_i+1, y_i+1), i=1,2,…,N-1. Поворот считается левым, если направление те-

кущего отрезка пути a_i+1 меняется относительно предыдущего отрезка a_i

в левую сторону, т.е. против часовой стрелки.

Таким образом, решение задачи сводится к вычислению количе- ства пар участков пути a_i и a_i+1, для которых выполняется условие [a_i × a_i+1]>0. Координаты векторов a_i и a_i+1 вычисляются через координа- ты точек (x_i, y_i): a_i=(x_{i –} x_i-1, y_{i –} y_i-1), a_i+1=(x_{i+1 –} x_i, y_{i+1 –} y_i), следовательно,

[a_i × a_i+1]= (x_{i –} x_i-1) (y_i+1- y_i) – (y_{i –} y_i-1)(x_{i+1 –} x_i), i=2, …, N-1.

Задача 2. «Здесь будет город-сад». Жители одного дома города Х решили высадить у себя во дворе несколько деревьев. Так как жильцы не смогли договориться, как должны быть расположены посадки, то каждый посадил дерево в том месте двора, где ему захотелось. После проведения посадок полученный сад решили обнести забором. Но пока доски не привезли, деревья обвязали одной длинной веревкой.

Исходная информация: N – количество деревьев в саду, (x_i, y_i) – координаты деревьев, i=1,2, …, N. Так как были высажены молодые са- женцы, то их толщиной можно пренебречь.

Требуется определить, к каким из посаженных деревьев надо привязать веревку так, чтобы все деревья оказались внутри обнесенной зоны, а длина веревки была минимальная.

Эта и подобные ей задачи сводятся к определению для заданного множества точек на плоскости выпуклой оболочки, то есть выпуклого многоугольника с вершинами в некоторых точках из заданного множе- ства, охватывающего все его точки. В [2] приведено несколько вариан- тов решения такой задачи с учетом временных затрат на выполнение алгоритмов. Здесь мы рассмотрим способ, использующий свойства ска- лярного произведения векторов.

Будем строить выпуклую оболочку в порядке обхода участка по часовой стрелке. Найдем самую левую точку М₀=(x₀, y₀), x₀=min{x_i}. Ес- ли таких точек несколько, то возьмем самую нижнюю из них. Эта точка наверняка принадлежит искомой выпуклой оболочке. Зададим первона- чальный вектор a₀ с началом в точке (x₀, y₀), параллельный оси Oy.

Следующей точкой оболочки будет такая точка М₁, чтобы вектор a₁ с началом в точке М₀ и концом в точке М₁ образовывал с первона- чальным вектором a₀ минимальный угол. Если таких точек несколько, то выбирается точка, расстояние до которой максимально.

Далее процесс продолжаем, то есть ищем точку М₂ с минималь- ным углом между вектором a₁ и вектором a₂ с началом в точке М₁ и концом в точке М₂, затем точку М₃ и т.д. Процесс прекращаем, когда

дойдем до первой выбранной точки или количество точек в оболочке станет равно N.

Для определения угла между векторами используется скалярное произведение. Причем сам угол можно не вычислять, так как мини- мальному углу соответствует максимальный косинус угла.

Задача 3. «Заяц» [3]. Недалеко от города Х находится зоосад. Здешний житель, заяц, хаотично прыгая, оставил след в виде замкну- той самопересекающейся ломаной, охватывающей территорию его владения. Найти площадь минимального по площади выпуклого много- угольника, описанного вокруг этой территории.

В данной задаче необходимо не только найти выпуклую оболочку множества точек, но и вычислить площадь выпуклого многоугольника с заданным набором вершин.

Исходные данные: N – количество вершин выпуклого много- угольника, (x_i, y_i) – координаты вершин, i=1,2, …, N.

Требуется определить площадь выпуклого N-угольника.

Площадь N-угольника может быть вычислена как сумма площадей треугольников, из которых N-угольник составлен. Для нахождения площади треугольника используем векторное произведение. Длина век- торного произведения векторов, как известно, равна удвоенной площа- ди треугольника, построенного на этих векторах. Пусть вершины тре- угольника расположены в точках A=(x₁, y₁), B=(x₂, y₂), C=(x₃, y₃). Совме- стим начало координат с первой точкой. Векторное произведение равно

x2

[AB × AC]= x3

i

-   x1

-   x1

j                 k

y2  - y1             0

y3 - y1             0 ,

следовательно, площадь треугольника равна S_ABC=1/2 ((x_{2 –} x₁) (y₃ – y₂) – (y_{2 –} y₁)(x_{3 –} x₂)).

Значение величины S_ABC может быть как положительным, так и отрицательным числом, так как оно зависит от взаимной ориентации векторов AB и AC, поэтому говорят, что площадь ориентированная.

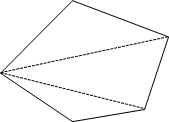
Для нахождения площади N-угольника последний требуется раз- бить на треугольники и найти сумму ориентированных площадей этих треугольников. Разбиение N-угольника на треугольники можно прове- сти так: зафиксировать одну из вершин N-угольника, например, первую A₁=(x₁, y₁) и рассматривать все треугольники A₁A_i A_i+1, i=2, 3,…, N-1.

А₂

А₃

А₁

А5                                                                                                                                      А

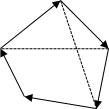
Рис. 16.4. Иллюстрация к задаче «Заяц»

Заметим, что аналогичным способом можно находить площадь произвольного многоугольника.

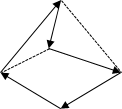Рис. 16.5. Нахождение площади произвольного многоугольника

Использование свойства ориентации площади треугольника, вы- численной по векторному произведению, позволяет определить, являет- ся ли заданный многоугольник выпуклым. Для выпуклого многоуголь- ника все треугольники, образованные тройками соседних вершин в по- рядке их обхода, имеют одну ориентацию. Поэтому проверка много- угольника на выпуклость может быть проведена с помощью последова- тельного сравнения знаков векторных произведений для всех пар сосед- них сторон многоугольника.

Задача 4. «Тигр в загоне». Недалеко от города Х находится за- поведник, в котором обитают уссурийские тигры. Работники заповед- ника очень переживают, когда тигр покидает охраняемую зону. Про- грамма охраны уссурийских тигров предусматривает снабжение каж- дого тигра ошейником с радиомаяком. Сигнал от тигриного радиомая- ка поступает в центр охраны и позволяет определить местоположе- ния тигра. Территория заповедника представляет собой произвольный многоугольник.

Исходные данные: N – количество вершин многоугольника, зада- ющего заповедник, (x_i, y_i) – координаты его вершин, i=1,2, …, N. (X, Y) – координаты точки, в которой находится тигр.

Требуется определить, находится ли тигр на территории заповед- ника, или надо срочно снаряжать спасательную экспедицию.

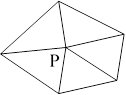
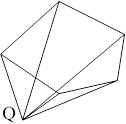
Рис. 16.6. Иллюстрация к задаче «Тигр»

Очень часто при решении задач геометрического содержания тре- буется проверить, лежит ли заданная точка внутри или вне многоуголь- ника. Таким способом можно решить, например, задачу о Бармаглоте, проверяя каждую точку Бармаглота относительно одеяла- многоугольника. Есть много способов проверки принадлежности точки многоугольнику, однако мы приведем здесь один из них, основанный на использовании произведения векторов.

Идея метода заключается в том, чтобы определить сумму углов, под которыми стороны многоугольника видны из проверяемой точки. Если точка лежит внутри многоугольника, то суммарный угол равен 2π (точка Р на рисунке), если же точка лежит вне многоугольника, то сум- ма углов не равна 2π (точка Q).

Таким образом, для решения надо перебрать в цикле последова- тельно все вершины многоугольника и найти сумму углов между векто- рами PA_i и PA_i+1, i=1,2, …, N. Не забудьте добавить угол между векто- рами PA_N и PA₁. Для определения величины угла между векторами нам потребуется формула скалярного произведения.

Так как стороны многоугольника должны рассматриваться после- довательно, в порядке обхода вершин, то при нахождении суммарного угла следует учитывать взаимное расположение векторов. Угол, под ко- торым сторона видна из исследуемой точки, может быть как положи- тельным, так и отрицательным. Для определения знака угла воспользу- емся векторным произведением. Знак векторного произведения и опре- делит знак конкретного угла в общей сумме.

Задача 5. «Пересечение отрезков». Дано n отрезков. Реализовать программу, находящую все их пересечения между собой. Отобразить решение графически.

На плоскости заданы два отрезка a и b, a – точками A¹(A¹ ,A¹ ) и

x        y

A²(A²_x,A²_y), а b – точками B¹(B¹_x,B¹_y) и B²(B²_x,B²_y). Найти и напечатать возможную точку их пересечения C(C_x,C_y). Рассмотрим первый отрезок

a. Уравнение прямой, на которой он лежит можно записать так: x_a = A¹_x + t_a (A²_x – A¹_x)

y_a = A¹_y + t_a (A²_y – A¹_y)

Здесь, A¹_x,A¹_y,A²_x,A²_y – константы, x_a,y_a – точки принадлежащие отрезку, при t_a изменяющемся от 0 до 1. Аналогично для отрезка b:

x_b = B¹_x + t_b (B²_x – B¹ ) y_b = B¹_y + t_b (B²_y – B¹_y)

Таким образом, приравнивая соответствующие координаты, полу- чаем задачу нахождения параметров t_a,t_b, при которых бы выполнялись равенства:

A¹_x + t_a (A²_x – A¹_x) = B¹_x + t_b (B²_x – B¹_x) A¹_y + t_a (A²_y – A¹_y) = B¹_y + t_b (B²_y – B¹_y)

После разрешения системы относительно t_a,t_b получаем: t_a (A¹_x – A²_x) + t_b (B²_x – B¹_x) = A¹_x – B¹_x

t_a (A¹_y – A²_y) + t_b (B²_y – B¹_y) = A¹_y – B¹_y

А это есть система из двух линейных уравнений относительно t_a,t_b. Известно, что система:

a₁ x + b₁ y = c₁ a₂ x + b₂ y = c₂

имеет следующее решение:

x = d_x/d y = d_y/d,

где d – определитель матрицы, d = a₁b₂ – a₂b₁,

d_x = c₁b₂ – c₂b₁, d_y = a₁c₂ – a₂c₁.

В нашей системе относительно t_a,t_b:

a1 = A1x – A2x b1 = B2x – B1x c1 = A1x – B1x

a2 = A1y – A2y b2 = B2y – B1y c2 = A1y – B1y

откуда легко находится d,d_x,d_y. Если d отличен от нуля, то система

имеет единственное решение. Правда, следует помнить, что искомые t_a,t_b – параметрически задают отрезки только если они лежат в диапа-

зоне [0,1], в противном случае точка пересечения прямых, на которых лежат отрезки, находится вне этих самых отрезков.

Если d равен нулю, а хотя бы один из d_x,d_y отличен от нуля, то от- резки лежат на параллельных прямых, или как говорят математики, они коллинеарны. Если же все три d,d_x,d_y равны нулю, то это значит, что от- резки лежат на одной и той же прямой, где опять возможны три случая

– либо отрезки не перекрываются, либо перекрываются в одной точке, либо перекрываются в бесконечном множестве точек.

Решение ряда задач повышенной сложности опирается на методы рассмотренные в комбинаторике, а именно на возможность генерации: сочетаний, перестановок, размещений и перечислений элементов.

Одним из важных элементов комбинаторики являются переста- новки. Перестановки без повторений – комбинаторные соединения, которые могут отличаться друг от друга лишь порядком входящих в них элементов. Число таких перестановок определяется как n!.

Для числа 3, количество перестановок будет равно 3! = 3 * 2 * 1 =

6. Для четырех: 4! = 4 * 3 * 2 * 1 = 24.

Часто для генерации перестановок используется алгоритм Дейкстры для получения всех перестановок по алфавиту. Разберем этот алгоритм.

Пусть у нас есть первая перестановка (например, 1234). Для нахождения следующей перестановки выполняем три шага.

1.    Двигаясь с предпоследнего элемента перестановки, ищем эле- мент a[i], удовлетворяющий неравенству a[i] < a[i + 1]. Для перестанов- ки 1234, это число 3, т. к. (3 < 4).

2.    Меняем местами элемент a[i] с наименьшим элементом, кото-

рый:

а) находится праве a[i].

б) является больше чем a[i]. В нашем случае меняем 3 и 4.

3.   Все элементы стоящие за a[i] сортируем. В нашем случае нужно

отсортировать число 4, но это единственный элемент, следовательно так его и оставляем.

В результате выполнения этих трех шагов получаем следующую по алфавиту перестановку 1243.

Выполнять эти шаги нужно циклически до тех пор, пока в пере- становке не будет находится искомый в первом шаге элемент a[i], т. е. пока перестановка не станет отсортированной по убыванию: 4321.

Перестановки с повторениями – комбинаторные соединения, в которых среди образующих элементов имеются одинаковые. В таких соединениях участвуют несколько типов объектов, причём имеется не- которое количество объектов каждого типа. Поэтому в выборках встре- чаются одинаковые элементы.

Задание 6. Гномики. Гномики решили встречать гостей с разно- цветными шарами. Раздай шарики гномикам так, чтобы цвет шарика не был такой же, как цвет колпачка, и чтобы у гномиков в одинаковых по цвету колпачках были шарики разного цвета и разной формы. Напиши- те программу, выводящую все возможные варианты раздачи шариков.

Рис. 16.7. Иллюстрация к задаче «Гномики»

Задание 7. Имеются цифры от 1 до 9 расположенные по возраста- нию (убыванию). Требуется расставить между ними произвольное ко- личество знаков <<плюс>> и <<минус>>, чтобы получилось выражение со значением 100. Например

123+4-5+67-89 = 100

9-8+76-5+4+3+21 = 100

Найти все возможные варианты таких выражений.

Задача 8. Дан двумерный массив, заполненный нулями и единица- ми. Найти прямоугольник, наибольшей площади, заполненный едини- цами.

Площадь прямоугольников изменяется от максимальной (весь мас- сив) до минимальной (прямоугольник, состоящий из одной 1). Каждый прямоугольник конкретной площади может быть построен множеством способов. Для площади S допустимый прямоугольник это такой, произ- ведение сторон которого, равно S. Мы должны для каждого значения площади перебрать все допустимые способы построения прямоугольни- ков. Каждый прямоугольник конкретной площади и формы может рас- полагаться в массиве различным образом. Точнее сказать, его левая верхняя вершина может находиться в разных точках массива. Следова- тельно, для прямоугольника определённой площади и формы мы долж- ны перебрать все возможные расположения.

Может показаться, что программа для большого массива будет ра- ботать слишком долго, но есть серьёзные возможности для её ускоре- ния. А именно:

1.            Если площадь перебирать от максимальной к минимальной, то первый найденный прямоугольник и будет искомым.

2.            Прямоугольник конкретной площади и формы не поместится в любом положении в массив.

Учёт этих утверждений ведёт к очень серьёзному ускорению про- граммы.

Задание 9. «Вирус». Колония клеток представляет собой квад- ратную матрицу порядка N (N < 500). В колонию проникает M (M < 11) вирусов, которые поражают клетки с координатами (X1, Y1), ... (Xm, Ym). За одну единицу времени вирус проникает в клетки, соседние с за- раженными (соседними считаются клетки, имеющие общую сторону). Требуется написать программу, которая определит время заражения всей колонии. Графически показать процесс заражения.

Задание 10. «Сундук Билли Бонса». Билли Бонс положил в сун- дук некоторое количество золотых монет. На второй год он вынул из сундука сколько-то монет. Начиная с третьего года, он добавлял столь- ко монет, сколько было в сундуке два года назад.

Требуется написать программу, определяющую количество монет в сундуке в первый и во второй года, если в X-м году там оказалось ровно Y монет. (3<=X<=20) и Y (1<=Y<=32767).

Пояснение: если в первый год положить 5 монет, а во второй год вынуть 3 монеты, то начиная с первого года в сундуке будет 5, 2, 7, 9,

16, 25, ... монет.

Скачано с www.znanio.ru