Информационно-познавательный проект Палиндромы в математике

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа № 10»

 

 

 

 

 

Информационно-познавательный проект

Палиндромы в математике

 

 

Автор:

Батятина Анастасия Андреевна,

обучающаяся 9б класса

МОУ «СОШ № 10»

 

Наставник:

Казакова Надежда Сергеевна,

учитель математики

МОУ «СОШ № 10»

 

 

 

 

 

 

 

Кыштым 2022

Оглавление

Введение………………………………………………………………………………………….3

Глава 1. Теория

1.1.Знакомство с палиндромами.. ……………...........……………………………………….....5

1.2.Именные палиндромы………………..…………………………………………….………..7

1.3. Числовой конструктор……………………………………………………………………..10

1.4. Свойства палиндромов…………………………………………………………………….12

Глава 2. Практика

2.1. Популярность чисел – палиндромов среди моих одноклассников…...………………...13

Заключение…….……………………...………………………………………………………...15

Список литературы……………….…………………………………………………………….16

Приложения……………………………………………..………………………………………17

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Нельзя представить человеческое общество, которое не знало бы никаких чисел. Старинные мифы повествуют, что знание числа некогда было привилегией богов.

Первая из наук - наука арифметика (от греческого слова «арифмои» -«число»). Первая она  не только потому, что возникла раньше всех других. Первая  по занимаемому среди  них положению.

Многие науки находятся в родстве  друг с другом (до недавнего времени  они и не подозревали об этом), но математика - это можно утверждать наверняка - в родстве со всеми.

Раз, два, три.… С этими словами вступаем мы царство чисел. Поначалу многие чувствуют себя в нем неуютно: всё здесь кажется окрашенным в серые тона, «климат» - скверным, «жизнь» - тоскливой.  Удручающее однообразие: десять повторяющихся значков-цифр составляют все население этого царства. Некоторые из них держаться поодиночке, другие собираются по двое, по трое, скапливаются большими группами, но сколько бы их ни было – все цифры одной и той же разновидности похожи друг на друга: любая из двоек – на все прочие двойки, пятерка – на пятерки, девятка – на девятки…  А о нуле и говорить нечего.

Впрочем, родство цифр основано не только на их внешнем сходстве, а – и в гораздо большей степени – на внутренней связи между ними.

   В конце концов – что такое двойка? Это две единицы.

   А тройка? Три единицы или одна единица и одна двойка.

   А четверка? Четыре единицы, или две двойки, или одна единица или одна тройка…

Какую цифру мы ни возьмем, в нее как бы вложена любая из предшествующих ей.   Это напоминает детскую игрушку – матрёшку.

Актуальность выбранной темы заключается в том, что числа и слова палиндромы и репьюниты являются одними из самых интересных и познавательных тем в математике. Они обладают необычными свойствами и такой же необычной историей. Многие подростки считают математику скучной наукой, из-за этого падает интерес к предмету, что отражается на результатах обучения. Благодаря универсальности палиндрома изучение таких предметов, как математика может стать более интересными, а так же использование нестандартных приемов в формировании вычислительных навыков помогает сэкономить время на уроке, успешно сдать экзамен.

Цель работы – знакомство и изучение «особенных»  чисел - репьюнитов, чисел-палиндромов.

Для реализации поставленной цели предлагается решить следующие задачи:

ü  Изучить числа палиндромы;

ü  Познакомиться с историей репьюнитов, чисел-палиндромов;

ü  Популяризировать знания о числах репьюнитах и палиндромах среди моих одноклассников

ü  Создать брошюру «Палиндромы в математике»

В ходе работы над проектом были использованы следующие методы:

Ø  поиск информации по теме;

Ø  обработка собранной информации;

Ø  опрос одноклассников;

Практическая значимость состоит в том, что материалы данного проекта могут применяться на уроках, факультативах и на занятиях  внеурочной деятельности. Данная работа также будет полезна всем тем, кто желает легче и лучше считать.

 

 

 

 

 

 

 

 

 

 

 

Глава 1.

1.1.Знакомство с палиндромами.

Палиндро́м (от греч. πάλιν — ≪назад, снова≫ и греч. δρoμος—≪бег≫) буквосочетание, слово или текст, одинаково читающиеся в обоих направлениях. Первые палиндромы появились в Древнем Риме, более 2000 лет тому назад. Ими украшали амфоры, чаши, вазы и другие предметы округлой формы. Такие надписи можно было читать в обе стороны, поворачивая сосуд в руках. Во фразах - палиндромах при чтении справа налево разорвутся слова, образуются новые, но порядок букв позволяет прочитать фразу и слева направо и справа налево. Палиндромы можно встретить не только в математике, но и в других науках, таких как литература, русский язык, английский, латинский, французский языки, химия, изобразительное искусство(Приложение 1).

Математические палиндромы обладают тем же свойством, т.е. число отличается симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным. Числа - палиндромы образуют одно из наиболее интересных подмножеств множества натуральных чисел.

Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо. Например: 676; 9559; 1881; 74947; 7622267 и т. д.

Палиндром можно получить как результат операций над другими числами. Так, в книге «Есть идея!» известного популяризатора науки Мартина Гарднера (Приложение 2) упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с обращённым числом, то есть записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не образуется палиндром.

Например, берем число 165,

165 + 561 = 726,

726 + 627 = 1353,

1353 + 3531 = 4884

Например, для числа 163:

163+361 = 524

524 + 425 = 949

А суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.

Но есть числа, для которых этот способ "не работает". Известно, что выполняя сложение примерно десять миллионов раз, не удается превратить числа 196 или 879 в палиндромное. И до сих пор не найдено ни на каком шагу из этих чисел получится палиндром, ни строгого доказательства, что палиндром не будет получен никогда.

Можно рассматривать не только сложение, но и другие операции, включая возведение в степень и извлечение корней. Вот несколько примеров того, как при их помощи из одних палиндромов получаются другие:

√ 484+3√ 1331=22+11=33

11⁰ = 1

11¹ = 11

11² = 121

11³ = 1331

11⁴ = 14641

 

 

 

 

 

 

 

 

 

 

 

1.2.Именные полиндромы

Палиндромы в математике встречаются в некоторых множествах чисел, удостоенных собственных названий: число Фибоначчи, Репдиджит, Репьюнит.

Числа Фибоначчи

Фибоначчи изучал математику и во время обширных путешествий познакомился с индийско-арабской системой счисления. Оттуда математик и узнал о числовой последовательности, которую в древней Индии использовали в стихосложении.

Числа Фибоначчи — это ряд, состоящий из целых чисел. Их особенность заключается в том, что каждый элемент представляет собой сумму двух предыдущих чисел.

Последовательность Фибоначчи начинается с 0 и 1. Продолжить ряд легко: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности. В этой последовательности каждое следующее число равно сумме двух предыдущих. Её назвали последовательностью Фибоначчи. 

Математик обратил внимание на числовую последовательность, когда думал о разведении кроликов. (Приложение 3)

Но больший интерес для исследователей представляет не сам ряд, а частное соседних чисел, равное, примерно 1,618 для всех элементов ряда. Эта пропорция больше известна как золотое сечение.

Это соотношение можно найти в предметах, которые нас отгружают: гармония в гранях снежинок, в расположении лепестков цветов, ячеек ананаса, завитки раковин у улитки — все подчиняется правилу золотого сечения. Даже строение нашего тела гармонично: если измерить наш рост и разделить на расстояние от пояса до ступней или длину руки на расстояние от локтя до кончиков пальцев, получится известное нам соотношение 1,618.

Репдиджит

Палиндром, составленный из одной и той же цифры, называют репдиджитом:

7777

888

22

 

Репьюниты

Репьюниты – натуральные числа, запись которых состоит только из единиц. В десятичной системе счисления репьюниты обозначаются короче Rn: R1 = 1, R2 = 11, R3 = 111 и т. д., и общий вид для них:sur001.wmf, n= 1, 2, 3…

Общий вид репьюнита может быть записан в другом виде:sur002.

Например: 11; 111; 1111; 11111; 111111; 1111111 и т. д.

Обнаружено немало интересных свойств репьюнитов:

Ø  Репьюниты – частный случай чисел-палиндромов, которые остаются неизменными при прямом и обратном прочтении.

Ø  Репьюниты относятся к таким палиндромам, которые делятся на произведение своих цифр.

Ø  Известно пять простых репьюнитов: R2, R19, R23, R317 и R1031, причем, что самое интересное – индексы этих репьюнитов также простые числа. Самое маленькое число репьюнит – 1. Самое большое – еще не найдено.

Ø  В семействе репьюнитов выявлено пока только 9 простых чисел: 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343 (индексы репьюнитов).

Ø  Раскладывая некоторые составные репьюниты на простые множители:

111 = 3•37

1111 = 11•101

11111 = 41• 271

1111111 = 239•4649

11111111 = 11•73•101•137

111111111 = 3•37•333667 и т. д. можно заметить числа палиндромы.

Ø  В результате умножения некоторых репьюнитов мы получили числа-палиндромы:

11•11 = 121

11•111 = 1221

1111•11 = 12221

111•111 = 12321

11111•111 = 1233321

11111•1111 = 12344321 и т.д.

Перемножив немало репьюнитов, можно сделать вывод о том, что каждый раз получается число-палиндром.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.3.Числовой конструктор

 

Из простых чисел-палиндромов, располагая их определённым образом, скажем

построчно, можно составить симметричные фигуры, отличающиеся оригинальным

рисунком из повторяющихся цифр.

Вот, например, красивая комбинация из простых палиндромов, записанных с помощью 1и 3. Особенность этого числового треугольника в том, что один итот же фрагмент повторяется трижды, не нарушая симметрию рисунка.

 

1

131

13331

1333331

131333131

                   13331113331(рисунок 1)

 

Легко увидеть, что общее количество строк и столбцов — число простое (17). К тому жепростые числа и суммы цифр: выделенных красным фрагментов (17); каждой строки, заисключением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и девятого столбцов

(7, 11) и «лесенки» из единиц, образующей боковые стороны треугольника (11). Наконец,

если двигаться параллельно указанным «сторонам» и складывать по отдельности цифры

третьего и пятого рядов (рис. 3), получим ещё два простых числа (17, 5).

 

1

131

13331

1333331

131333131

13331113331(рисунок 2)

 

Продолжая построение, можно сконструировать на основе данного треугольника болеесложные фигуры. Так, ещё один треугольник с аналогичными свойствами нетруднополучить, двигаясь с конца, то есть начать с последнего числа, вычёркивая на каждомшаге две одинаковые симметрично расположенные цифры и переставляя или заменяядругие — 3 на 1 и наоборот. При этом сами цифры следует выбирать с таким расчётом,чтобы образующееся в итоге число оказалось простым. Объединив обе фигуры, получимромб с характерным узором из цифр, скрывающим в себе немало простых чисел.В частности, сумма выделенных красным цветом цифр равна 37.

1

131

13331

1333331

131333131

13331113331

1311131

13331

313

1                                    (рисунок 3)

 

Пример 2. (Приложение 4)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.4. Свойства палиндромов

Познакомившись с палиндромами, изучив их историю, свойства можно сделать вывод, что с такими числами связано немало интересных закономерностей:

Ø  Читается слева направо и справа налево одинаково

Ø  Число знаков, используемых при записи чисел, может быть четным и нечётным

Ø  Существует единственный простой палиндром с чётным числом цифр – 11.

Ø  Первой и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Все простые двузначные числа, записанные с помощью перечисленных цифр (кроме 19), можно разбить на пары (Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97).

Ø  Среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1 (Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929).

Ø  Все однозначные числа являются палиндромами.

Ø  Можно получить как результат операций над другими числами:

- сложение

- возведение в степень

- извлечение корня

- умножение

Ø  Можно получить многоугольные фигуры

Ø  Являются представителями класса простых чисел

 

 

 

 

 

 

 

 

 

 

Глава 2.

2.1. Популярность чисел – палиндромов среди моих одноклассников.

       В рамках своего проекта я провела  опрос, задав несколько вопросов анкеты своим одноклассникам (Приложение 5), чтобы проанализировать знания ребят о палиндромах. В опросе приняли участие 21человек.

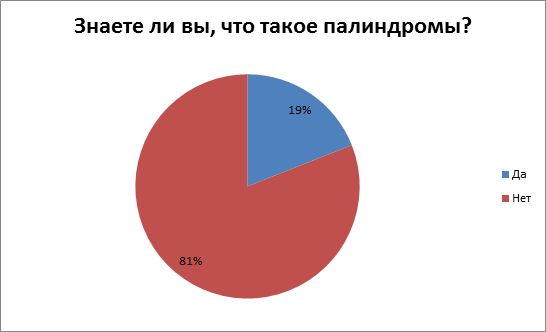
      На основе проведенного анкетирования, я получила  следующие результаты (Приложение 6):

     Вывод по каждой диаграмме:

1)      19 % моих одноклассников знает, что такое палиндромы, а 81% - нет.

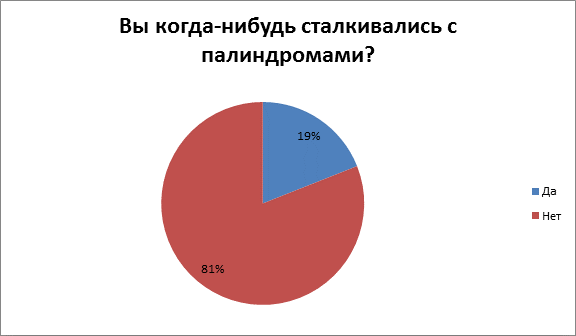
2)      19% моих одноклассников когда-то сталкивались с палиндромами, а 81%- нет.

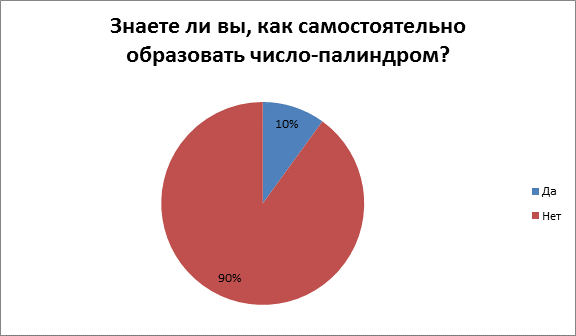
3)      10% - знают как самостоятельно образовать число-палиндром, а 90% - нет

4)      5% моих одноклассниковзнают разновидности палиндромов, а 95% - нет

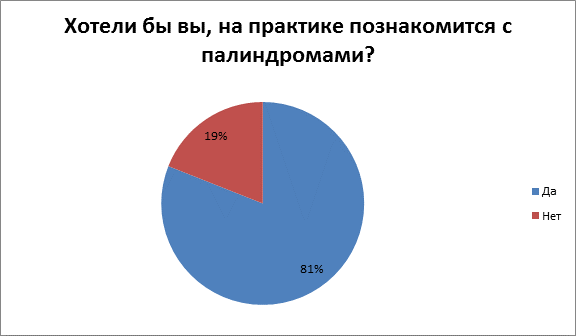
5)      81%  ребят хотели бы на практике познакомится с палиндромами, а 19% - нет.

           Проанализировав полученные результаты, я пришла к выводу, что большая часть моих одноклассников мало что знают о палиндромах и хотели бы познакомиться с ними поближе.

И тогда я сделала брошюру, которая знакомит с палиндромами, алгоритмом получения палиндрома, их разновидностями.

Я раздала брошюру одноклассникам и предложила с ее помощью познакомиться с палиндромами и выполнить простые задания. 11 человек приступили к решению заданий. (Приложение 7)

После, я проанализировала результаты:

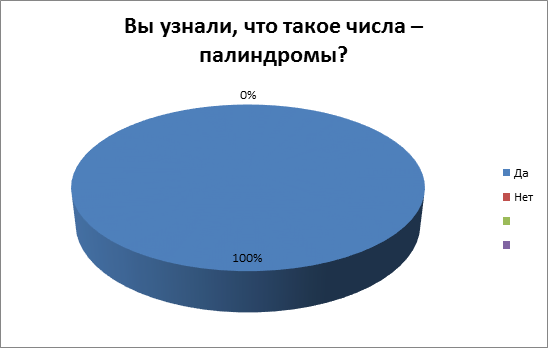
1)      100% ребят познакомились с палиндромами

2)      90% - было интересно, информация заинтересовала и увлекла

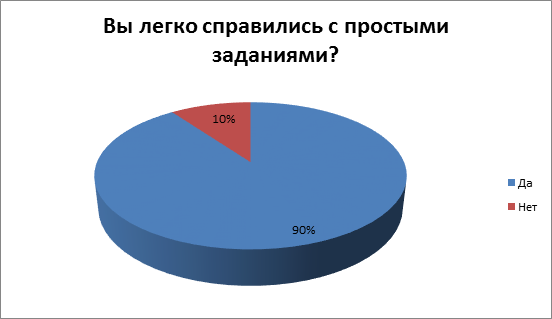
3)      90% - легко справились с простыми заданиями

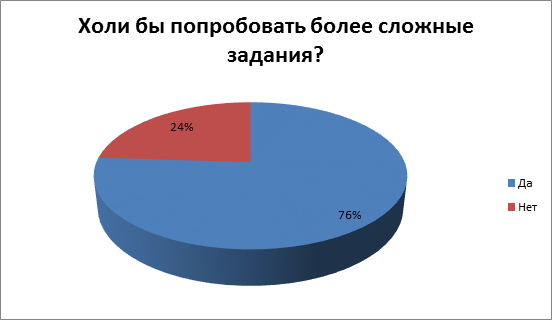
4)      А 76% ребят холи бы попробовать более сложные задания

Данные результаты показали, что моим одноклассникам материал в брошюре позволил познакомиться с числами палиндромами, их видами, а так же помог решить простые задания. Я считаю, что моя брошюра может быть  хорошим наглядным пособием, для  получения и запоминания информации о палиндромах, а также помощником в решении задач. Ею можно воспользоваться, как на уроках, так и на факультативах или в неурочное время для тренировки решения задач.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Заключение

Я познакомилась с удивительными натуральными числами: палиндромами. Пусть эти числа еще не до конца изучены, и не ясно их применение, но может быть в результате таких опытов с числами, и откроется их истинная суть.

Я узнала, что палиндромы, это не только интересные картинки в изобразительном искусстве, но и числа в математике, слова и фразы в русском языке. Мой кругозор стал шире, я узнала много интересной и полезной информации. Я думаю, что моё исследование поможет улучшить память, мышление, воображение.

Благодаря моему проекту ребята познакомились с числами – палиндромами, попробовали решить простые задачи.

Думаю, что представленная мной работа будет весьма интересна и полезна учащимся и всем увлекающимся математикой людям. Мир чисел настолько загадочен и увлекателен, что занимаясь данной работой, я поняла, если бы каждый из нас уделял ему больше внимания, то нашел бы для себя много нового и интересного.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список литературы

1)      Карпушина Н.М. Репьюниты и палиндромы// Математика в школе. – 2009, №6. – С.55 – 58.

2)      Перельман Я.И. Живая математика. – М.: «Наука», 1978.

3)      https://sch60rzn.ru/palindromy-v-matematike-start-v-nauke-simmetrichnyi-risunok-iz-palindromov/

4)      https://school-science.ru/9/7/44976

5)      https://school-science.ru/9/7/44976

6)      https://infourok.ru/issledovatelskaya-rabota-zagadochniy-mir-palindromov-3643404.html

7)      https://www.nkj.ru/archive/articles/17984/

8)      https://infourok.ru/nauchnoprakticheskaya-rabota-po-matematike-na-temu-palindromi-v-matematike-klassi-3072309.html

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложения.

Приложение 1.

Палиндромы встречаются в различных науках:

В литературе:

Ø  Аргентина манит негра.

Ø  Я иду с мечем судия.

Ø  А роза упала на лапу Азора (фраза из сказки «Буратино»).

В русском языке:

Ø  ШАЛАШ, РАДАР, ТОПОТ, КОК, КАЗАК — тоже палиндромы.

Английском языке:

Ø  «Madam, I’mAdam» («Мадам, я— Адам,— представился первый человек первой женщине)

Латинскомязыке:

Ø  Sumsummusmus (Я— сильнейшая мышь)

Финскомязыке:

Ø  Saippuakivikauppias (самое длинное в мире слово-палиндром)

В изобразительном искусстве

В химии:

Формула щавелевой кислоты

 

Приложение 2

Мартин Гардер

 

 

Приложение 3

Задача была поставлена следующим образом: «Если новорожденную пару кроликов, самца и самку, поместить в поле, то сколько пар кроликов будет через год?». Но как известно, ни одну практическую задачу невозможно решить без некоторых ограничений и предположений.  Поэтому, к условию задачи добавились следующие допущения:

Ø  Кролики не умирают;

Ø  Кролики достигают половой зрелости за один месяц;

Ø  Срок беременности у кроликов – один месяц;

Ø  Достигнув половой зрелости, кролики-самки рожают ежемесячно кролика-самца и кролика-самку.

Схема разведения кроликов выглядит следующим образом:

Так как по условию задачи в поле поместили новорожденных кроликов, то спариваться они не могут, так как не достигли половой зрелости. Через месяц кролики начинают спариваться и еще через один – рождается первая пара потомков. «Родители» продолжают наращивать потомство, а дети месяц ждут своего взросления, чтобы тоже стать родителями. В итоге, через 3 месяца по полю будут бегать три пары кроликов. Через 4 месяца уже 5 пар, а через 5 месяцев – 8.

Уже прослеживается закономерность. В конце каждого месяца количество пар кроликов будет больше, чем в предыдущем месяце ровно на столько, сколько пар было два месяца назад.

 

Приложение 4

Другой пример — треугольник, полученный из исходного после добавления к нему шести простых палиндромов (рис. 1). Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Её окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и ещё столько же — «боковые стороны» треугольника.

Рис. 1

Конечно, не обязательно ограничиваться двумя цифрами и требовать наличия в записи каждого используемого числа всех указанных цифр. Скорее, наоборот: ведь именно их необычные сочетания придают своеобразие узору фигуры. В подтверждение этому приведём несколько примеров красивых палиндромических зависимостей (рис. 2-4).

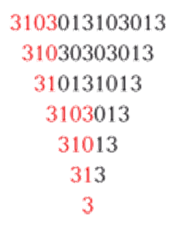
Рис. 2

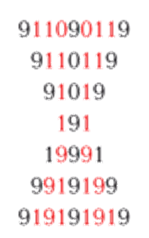
Рис.3

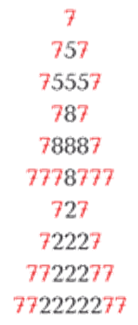
Рис. 4

Приложение 5

Опрос

1. Знаете ли вы, что такое палиндромы?

А) да

Б) нет

2. Вы когда-нибудь сталкивались с палиндромами?

А) да

Б) нет

3.Знаете ли вы, каксамостоятельно образовать число-палиндром?

А) да

Б) нет

4. Знаете ли вы разновидности палиндромов?

А) да

Б) нет

5. Хотели бы вы, на практике познакомится с палиндромами?

А) да

Б) нет

 

Приложение 6.

Приложение 7

1)      Вы узнали, что такое числа – палиндромы?

А) Да

Б) Нет

2)      Понравилась ли вам информация из брошюры?

А) Да

Б) Нет

3)      Вы легко справились с простыми заданиями?

А) Да

Б) Нет

 

4)      Холи бы попробовать более сложные задания?

А) Да

Б) Нет

 

 

Приложение 8

 

              

 

             

             

 

Скачано с www.znanio.ru