ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ В ЭКОНОМИКЕ

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ В ЭКОНОМИКЕ

Изложены примеры с экономическим характером и их решения путем применения интегральных исчислений.

В современных условиях возрастают требования к выпускникам финансово-экономических учебных заведений, как специалистам: по составлению прогнозов, оптимизации принимаемых решений и выбору экономической политики, применения электронно-вычислительной техники.

            Выпускники должны иметь фундаментальную математическую подготовку с усилением ее прикладной экономико-вычислительной направленности.

Активное использование задач с экономико-вычислительным содержанием на всех этапах учебного процесса развивает творческие способности учащихся, формирует экономическое мышление.

Для специалистов экономического направления математика является в большей мере инструментом анализа, организации, управления.

В курсе микроэкономики часто рассматривают так называемы предельные величины, т.е. для данной величины, представляемой некоторой функцией у =f(x), рассматривают ее производную f'x. Например, если дана функция издержек С в зависимости от объема q выпускаемого товара С = С(q), то предельные издержки будут за­даваться производной этой функции МС = С'(q). Ее экономический смысл - это издержки на производство дополнительной единицы выпускаемого товара. Поэтому часто приходится находить функ­цию издержек по данной функции предельных издержек.

Рассмотрим следующий пример. Дана функция предельных издержек МС = Зq² – 48q + 202, 1 ≤ q ≤ 20. Найти функцию издержек С = С(q) и вычис­лить издержки в случае производства 10 единиц товара, если из­вестно, что издержки для производства первой единицы товара со­ставили 50 тенге. [Пискунов Н.С.  Дифференциальное и интегральное исчисления для втузов, Том 2 -М. :Наука, 1985.-560с]

Для решения данной задачи следует определить функцию издержек находим интегрированием:

C(q ) = ,

где константа Со находится из данного условия С(1) = 50, так что С₀ = 50, поскольку интеграл обращается в нуль. Интегрируя, полу­чим функцию издержек

C(q) = q.

Подставляя q = 10 в полученную формулу, находим искомое значение

С(10) = 670.

Еще одним примером приложения определенного интеграла является нахождение  дисконтированной стоимости денежного потока.

Допустим вначале, что для каждого дискретного момента времени t = 1, 2, 3, ... задана величина денежного потока R((t). Если ставку процента обозначить через р, то дисконтированную стоимость каждой из величин R(1), R(2), R(3), ... найдем по известным формулам:

R(1)(1 + p), R(2)(1 + p), R(3)(1 + p), … .

Тогда дисконтированную стоимость денежного потока найдем, суммируя эти величины:

П = ,

где п - общее число периодов времени.

В непрерывной модели время изменяется непрерывно, т.е. для каждого момента времени 0 ≤ t ≤ Т, где [0, T] - рассматриваемый период времени, задана величина I(t) - скорость изменения денеж­ного потока (т.е. величина денежного потока за промежуток времени от t до t + dt приближенно равна I(t)dt. Для получения ве­личины П изменим формулу П = .А именно, знак суммирования заменим на знак определенного интеграла, формулы вычисления дисконтированной стоимости в дискретном случае заменим на их непрерывный аналог, и тогда формула П = , примет следую­щий вид:

П = .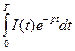

Пример. Под строительство гидроэлектростанции задан непрерывный денежный поток со скоростью I(t) = -t² +20t +5  (млрд. тенге/год) в течение 20 лет с годовой процентной ставкой р = 5%. Найти дисконтированную стоимость этого потока. [[Пискунов Н.С.  Дифференциальное и интегральное исчисления для втузов, Том 2 -М. :Наука, 1985.-560с]

]

Решение. По формуле П = 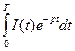 имеем

П = .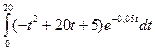

Чтобы вычислить этот интеграл, выполним сначала замену переменной:

s = -0,05t,  t = -20s,  dt = -20ds.

При этом новые пределы интегрирования получаются подстановкой старых пределов в формулу замены: s = 0, s  = -1. Имеем

-

П = -20(- 400s² – 400s + 5)e = 20  (- 400s² – 400s +5)eds.

К последнему интегралу применим формулу интегрирования по частям, полагая и = -400s - 400s + 5, dи = (-800s - 400)ds, dv = eds, v= е. Поэтому

П = 20 ((-400s² - 400s + 5)е + е(800s + 400)ds .

В первом слагаемом подставим пределы интегрирования, а ко вто­рому слагаемому еще раз применим формулу интегрирования по частям, полагая и = 800s + 400, dи = 800ds. Имеем

П = 20 (5 – 5e + (800s + 400)e800eds) =

= 20(5 - 5е - 1 +400 + (800 - 400)e   - 1 - 800 + 800е - 1) =

 = 20(1195е- 1 -395).

Окончательно получим П = 892 (млрд. тенге).

Далее рассмотрим некоторую модель экономического роста, предложенную Е.Д. Домаром. Основные допущения этой моде сформулированы ниже.

1 . Всякое изменение величины скорости денежного потока I(t) влияет как на совокупный спрос, так и на изменение объема производства.

2. Скорость изменения величины спроса Y(t) пропорциональна производной скорости денежного потока с коэффициентом пропорциональности K = 1/s, где s - предельная величина накопления. Это предположение можно записать в виде уравнения

3 Экономический потенциал к (т.е. величина стоимости товара которые можно произвести) пропорционален объему оборотных средств  К с  коэффициентом   пропорциональности  р,  k = рК. Дифференцируя по t, получим

.

В модели Домара предполагается, что весь экономический по­тенциал полностью используется, иными словами, У =  к. Диффе­ренцируя по t, получим

.

Подставляя   и   в , имеем

 = pI, .

Чтобы найти функцию I(t) из уравнения  = pI, , проинтегрируем обе части последнего равенства по t от 0 до t. Получим

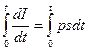, или ln|I(t)| = pst,

Откуда ln|I| = ln|I(0)| + pst. Потенцируя последнее равенство, получим окончательное выражение для I(t):

I(t) = I(0)e,

где I(0) – это скорость денежного потока в начальный момент времени.

Таким образом, для того чтобы поддерживать равновесие между объемом производимых благ и совокупным спросом на них, скорость денежного потока должна расти с экспоненциальной скоростью согласно формуле

I(t) = I(0)e

Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.

Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем,  и свойства определенного интеграла, в частности. Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл   - это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.

Скачано с www.znanio.ru