ИСПОЛЬЗОВАНИЕ ТЕОРЕМ О ПОЧЛЕННОМ

Использование теорем о почленном
умножении и сложении неравенств
при оценке значения выражения

Цели: закрепить знание теорем о почленном сложении и умножении неравенств; формировать умение применять данные теоремы для оценки значения выражения; формировать умение решать задачи повышенной трудности.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Известно, что –5 < а < 9. Оцените значение выражения:

а) 2а;        б) –4а;        в) ;        г) –а;        д) а + 4;        е) 3 – а.

2. Пусть b – произвольное число, сравните с нулём значение выражения:

а) – b² – 16;                                г) (b – 2)² + 16;

б) 13 + b²;                                   д) (15b – 127)² + (1 – b)².

3. Известно, что х > 5, у > 15. Оцените значение выражения:

а) х + у;                            б) х · у;                       в) 2х + у;

г) 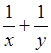;            д) –2ху;                     е) х² – 25.

III. Формирование умений и навыков.

1. А к т у а л и з а ц и я   з н а н и й.

При выполнении устной работы учащиеся использовали теоремы о почленном сложении и умножении неравенств и следствие. Просим их сформулировать данные теоремы.

2. Р а б о т а   п о   у ч е б н и к у.

Теоремы о почленном сложении и умножении неравенств используются для оценки суммы, разности, произведения и частного. Разбираем примеры 1–4 на с. 162–163 учебника. Еще раз обращаем внимание на удобную запись неравенств (одного под другим) при выполнении почленного сложения либо умножения.

3. № 770.

4. Докажите, что если 0 < а < 7 и 0 < b < 3, то:

а) 5а + 11b < 70;            в) аb + 4 < 30.

Р е ш е н и е

а) 0 < а < 7;                        0 < 5а < 35

    0 < b < 3;                      0 < 11b < 33    

                                       0 < 5а + 11b < 68

Так как 68 < 70, то 0 < 5а + 11b < 70.

б)   0 < а < 7;

      0 < b < 3;  

     0 < аb < 21;               4 < аb + 4 < 25

Так как 25 < 30, то         4 < аb + 4 < 30.

5. В этих упражнениях демонстрируется практическое применение теорем о почленном сложении и умножении неравенств.

№ 772.

Р е ш е н и е

Пусть а – основание, b – боковая сторона равнобедренного треугольника, тогда Р = а + 2b – периметр этого треугольника.

41 ≤ b ≤ 43;                    82 ≤ 2b ≤ 86

                                         26 ≤ а ≤ 28        

                                   108 ≤ а + 2b ≤ 114.

О т в е т: 108 ≤ Р ≤ 114.

№ 774.

Р е ш е н и е

Пусть а и b – длина и ширина прямоугольной комнаты, тогда её площадь равна аb.

      7,5 ≤ а ≤ 7,6

     5,4 ≤ b ≤ 5,5   

40,5 ≤ а · b ≤ 41,8.

Так как требуется комната площадью не менее 40 м² (то есть S ≥ 40), то данное помещение подойдёт для библиотеки.

О т в е т: да.

№ 775.

Пусть α, β – углы треугольника, тогда третий угол γ по теореме о сумме углов треугольника равен 180 ° – α – β.

  58° ≤ α ≤ 59°;                                            –59° ≤ –α ≤ –58°

102° ≤ β ≤ 103°;                                 –103° ≤ –β ≤ –102°                           

                              180° – 59° – 103° ≤ 180° – α – β ≤ 180° – 58° – 102°

                                                         18° ≤ 180° – α – β ≤ 20 °.

О т в е т: 18° ≤ γ ≤ 20°.

6. Задания повышенной трудности можно предложить сильным в учебе учащимся или решать с классом, если останется время.

№ 777.

Р е ш е н и е

Пусть ABCD – выпуклый четырёхугольник, тогда его диагонали пересекаются в т. О.

Докажем, что AB + DC < AC + BD и BC + AD < AC + BD.

:

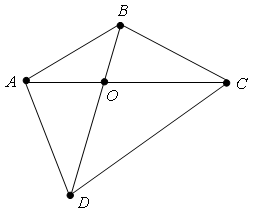
Воспользуемся неравенством треугольника (каждая сторона треугольника меньше суммы двух других сторон).

1)            AB < AО + BО

               DC < ОD + ОС                

    AB + DC < AО + BО + DО + ОС;

    AB + DC < (AО + ОС) + (BО + ОD);

    AB + DC < AC + BD.

2)           BC < BО + СО

               AD < OA + OD                

   BC + AD < BО + CO + OA + ОD;

   BC + AD < (BО + ОD) + (CO + OA)

   BC + AD < BD + AC.  

№ 778.

Р е ш е н и е

Медианы треугольника ABC пересекаются в одной точке О. Обозначим длины сторон треугольника a, b, c. АА_1, ВВ₁, СС₁ – медианы.

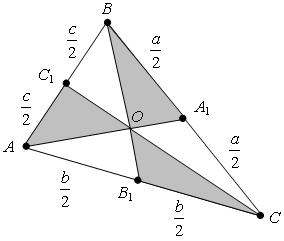
1) Докажем, что сумма длин медиан треугольника больше его полупериметра.

: воспользуемся неравенством треугольника.

2) Докажем,  что  сумма  длин  медиан  треугольника  меньше  его  периметра.

Предлагаем учащимся решить самостоятельно (можно дать в качестве домашнего задания).

IV. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Сформулируйте основные свойства числовых неравенств.

– Сформулируйте теоремы о сложении и умножении числовых неравенств.

– Каким образом используют теоремы о сложении и умножении числовых неравенств при оценке значения выражения?

Домашнее задание.

1. № 771, № 773.

2. Верно ли, что:

а) если а > 4 и b > 6, то 2a + b > 45;

б) если a > 3 и b > 9, то 3ab > 30.

3. Сравните, если возможно:

а) 3а + 2b и 16, если а > 4 и b > 8;

б) 5а – b и 20, если а > 4 и b < –3.

4. № 776 (б)*.