"Исследование функции по графику ее производной". Алгебра. 10 класс

Применение производной.

Тема № 5. Исследование функции по графику ее производной.

В предыдущих заданиях осуществлялось исследование функции по ее графику. В этих примерах задавался график функции, на котором было видно, где функция возрастает, где убывает, где у нее  максимумы или минимумы. Если  задается график не самой функции, а ее производной, то в таких примерах для ответа на вопросы, надо применить изученную теорию. (Повторите темы №3 и №4: «Исследование функции на монотонность» и «Исследование на экстремумы»).

Пример. Задан график производной некоторой функции. По графику ответить на вопросы. (цветных линий на исходном графике нет, проведены позже). 

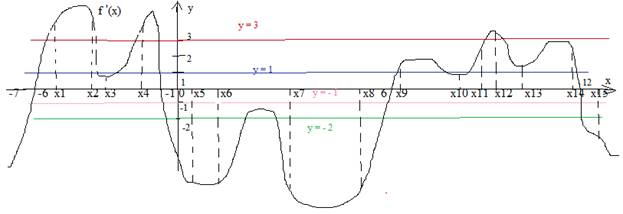
Вопросы.

1.      Количество промежутков возрастания функции.    Пояснение: Функция возрастает там, где производная положительна, т.е. это те  участки графика производной, которые лежат выше оси х. Это промежутки [ -6; -1] и [ 6 ;12].

Ответ:   2    

2.      Длина н наибольшего участка возрастания. 

Посчитаем длину первого второго промежутки и выберем наибольшую длину.

-1 –(-6) = -1 + 6 =5               12 – 6 = 6             

   Ответ:   6  

3.       Длина  наименьшего участка возрастания.       Ответ:   5  

4.      Количество промежутков убывания.

Функция убывает там, где производная отрицательна, т.е. это те  участки графика производной, которые лежат ниже оси х. Это промежутки ( - ∞; -6] ,      [ -1 ; 6 ] и [12; + ∞]

Ответ:   3    

5.      Длина  наименьшего участка убывания.

Наименьший участок по длине [ -1 ; 6 ], т.к. длины, содержащие бесконечность вычислить нельзя. Его длина  6 – ( -1) = 6 +1 = 7.           Ответ:   7    

6.       Сколько точек Х₁…Х₁₅ , в которых функция возрастает.

Надо подсчитать, сколько точек попадает на участки возрастания, то есть на те  участки графика производной, где производная  f  ´(x) > 0, участки которые располагаются выше оси ОХ.  Это точки Х₁, Х_2, Х₃ Х₄, Х₉,  Х₁₀, Х₁₁, Х₁₂, Х₁₃ Х_14. Ответ:   10    

7.      Сколько точек Х₁…Х_15,  в которых   функция убывает.

Надо подсчитать, сколько точек попадает на участки убывания, то есть на те  участки графика производной, где производная  f  ´(x) < 0, участки которые располагаются ниже оси ОХ.  Это точки Х₅, Х₅,  Х₇, Х₈, Х_15. Ответ:   5

8.      Сколько точек, где касательная к графику функции (не к графику производной) параллельна оси ОХ.

По условию касательная параллельна оси ОХ, значит, производная в этих точках равна нулю f  ´(x) = 0. На графике функции это точки экстремума, а на графике производной, который у нас задан, это точки пересечения с осью ОХ. Надо подсчитать, сколько  таких точек. Это точки Х= - 6, Х= -1, Х=6, Х=12.

Ответ:   4

9.      Сколько точек, где угол наклона касательной к графику функции равен 45°.

Производная связана с углом наклона касательной к графику функции соотношением: f  ´(x₀) = tg a  Если угол наклона касательной равен 45°, tg 45°=1

f  ´(x₀) =1. Проведем на графике прямую y =1 ( дополнительная  синяя прямая)

и подсчитаем, сколько получилось точек пересечения с нашим графиком.

Ответ:   8

10.  Сколько точек, где угол наклона касательной к графику функции равен 135°.

Если угол наклона касательной равен 135°, tg 135°= -1

f  ´(x₀) = -1. Проведем на графике прямую y = -1 ( дополнительная  розовая прямая) и подсчитаем, сколько получилось точек пересечения с нашим графиком.       Ответ:   4

11.  Сколько точек, где угловой коэффициент наклона касательной к графику функции равен 3.

Производная связана с угловым коэффициентом наклона касательной к графику функции соотношением: f  ´(x₀) = к    к – угловой коэффициент.

Уравнение любой прямой имеет вид:  у=кх + b.  Так как у нас к=3, то надо провести дополнительную прямую у=3 (коричневая прямая) и подсчитать, сколько получилось точек пересечения с нашим графиком.       Ответ:   6

12.  Сколько точек, где касательная к графику функции (не к графику производной) параллельна прямой у = 5 – 2х.

Так как у нас к= -2, то надо провести дополнительную прямую у= -2 (зеленая прямая) и подсчитать, сколько получилось точек пересечения с нашим графиком.       Ответ:   6

13.   а) Сколько точек, где касательная к графику функции (не к графику производной) параллельна прямым  у =  - 8 или у = - 0,5 или у =10.

б) найти сумму абсцисс этих точек.

а) Для всех этих прямых угловой коэффициент равен 0 (в уравнении касательной у=кх + b множитель, стоящий перед Х отсутствует, т.е. к =0). f  ´(x₀) = 0 на графике функции это точки экстремума, а на графике производной, который у нас задан, это точки пересечения с осью ОХ. Надо подсчитать, сколько  таких точек. Это точки Х= - 6, Х= -1, Х=6, Х=12.      а)   Ответ:   4

б) Подсчитаем сумму абсцисс этих точек   - 6+ (- 1)+6 +12 =11.

б)   Ответ:   11

14.    Количество экстремумов функции.

 В точках экстремума производная равна нулю и меняет знак при переходе через это точку. Х= - 6, Х= -1, Х=6, Х=12.

Ответ:   4

15.   а)  Количество точек максимума, б) Сумма абсцисс точек максимума.

Максимум функции бывает в тех точках, при переходе через которые производная меняет свой знак с плюса на минус. (т.е. до этой точки график находился выше оси ОХ, а после этой точки график лежит ниже оси ОХ.). В нашем примере это точки Х= -1 и  Х=12. В этих точках производная поменяла знак с (+) на ( - ).           а)   Ответ:   2

б) Подсчитаем сумму абсцисс этих точек   - 1 + 12 = 11.    б)   Ответ:   11

16. а)  Количество точек минимума, б) Сумма абсцисс точек минимума.

Минимум функции бывает в тех точках, при переходе через которые производная меняет свой знак с  минуса на плюс. (т.е. до этой точки график находился ниже оси ОХ, а после этой точки график лежит выше оси ОХ.). В нашем примере это точки Х= -6 и  Х=6. В этих точках производная поменяла знак с (-) на ( + ).           а)   Ответ:   2

б) Подсчитаем сумму абсцисс этих точек   - 6 + 6 = 0.    б)   Ответ:   0

17.  Наименьшая точка максимума.

Точки  максимума Х= -1 и  Х=12. Наименьшая Х= -1. Ответ:   - 1

18.  Наибольшая точка минимума.

Точки  минимума Х= -6 и  Х=6. Наибольшая Х= 6. Ответ:   6

19.   В какой точке на промежутке [ -1;6 ] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

а) На промежутке [ -1;6 ] график производной находится ниже оси ОХ. На этом промежутке производная отрицательна,  сама функция убывает и ее график пойдет вниз.  Наибольшее значение примет в т. Х= -1, наименьшее значение в т. Х= 6.         а)   Ответ:   -1 б)   Ответ:   6

20.   В какой точке на промежутке [ 6 ; 12 ] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

а) На промежутке [ 6;12 ] график производной находится выше оси ОХ. На этом промежутке производная положительна,  сама функция возрастает и ее график пойдет вверх.  Наибольшее значение примет в т. Х=12, наименьшее значение в т. Х=6        а)   Ответ:   12      б)   Ответ:   6

Выполнить самостоятельно.

Задан график производной  функции. По графику ответить на вопросы (ответы записывать без пояснений).

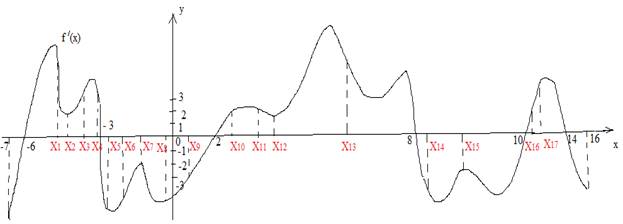
1.      Количество промежутков возрастания.

2.      Длина а) наибольшего промежутка возрастания; б) наименьшего промежутка возрастания.

3.      Количество промежутков убывания.

4.      Длина а) наибольшего промежутка убывания; б) наименьшего промежутка убывания.

5.      Сколько точек Х₁…Х_17,  в которых  функция возрастает.

6.      Сколько точек Х₁…Х_17,  в которых  функция убывает.

7.      Сколько точек экстремума имеет функция.

8.      Сколько точек максимума имеет функция ( перечислить и их количество).

9.      Сколько точек минимума имеет функция ( перечислить и их количество).

10.  Наименьшая точка максимума.

11.  Наибольшая точка максимума.

12.  Наименьшая точка минимума.

13.  Наибольшая точка минимума.

14.  Сколько точек, где касательная к графику функции параллельна оси ОХ.

15.  Сколько точек, где угол наклона касательной к графику функции равен 45°.

16.  Сколько точек, где угол наклона касательной к графику функции равен 135°.

17.  Сколько точек, где касательная к графику функции (не к графику производной) параллельна прямой у = 15 + 3х.

18.  Сколько точек, где касательная к графику функции (не к графику производной) параллельна прямой у = - 3х + 8

19.  Сколько точек, где угловой коэффициент наклона касательной к графику функции равен  - 2 .

20.  а) Сколько точек, где касательная к графику функции  параллельна прямым  у = 2 ,  у = - 3  и  у =1,5.

б) найти сумму абсцисс этих точек.

21. В какой точке на промежутке [ -6 ; -3] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

22. В какой точке на промежутке [ 8 ; 1] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

Ответы на вопросы по графику производной.

1).    3

     2).   а)   6     б)  3

    3)    4

    4)   а)   6      б)  1

    5)  10

    6)   7

     7)   6

     8)   - 3

     9)   3

     10)  - 3

     11)   14

     12)    - 6

     13)    10

     14)    6

     15)    6

      16)    6

      17)     8

      18)     10

      19)     7

      20)     а)   6         б)  25

     21)     а)  наиб. в т. - 3      б) наим. в т.  – 6

     22)     а)  наиб. в т.  8       б) наим. в т.  1