Исследование функций на экстремумы. Алгебра и начала анализа 10 класс.

Применение производной.

Нахождение экстремумов ( максимумов и минимумов) функции.

Краткая теория. (Разобрать, записать в тетрадь основные понятия, ответить на вопросы по теоретической части) .

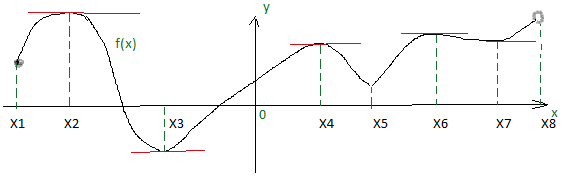
 Рисунок 1.  Рассмотрим внутренние точки области определения функции, изображенной на рис.1, в которых производная равна нулю или не существует. В точках, где производная равна 0, касательная параллельна оси ОХ. Это точки Х₂, Х₃, Х₄, Х₆ и Х₇.  В точке Х₅ касательную провести нельзя, т.к. острый график, поэтому в этой точке производная не существует.  На концах промежутка в точках Х₁ и Х₈ тоже касательные провести нельзя, так как нужна окрестность точки. На концах промежутка экстремумов не бывает.

Определение.  Точки, в которых производная функции равна 0 или не существует называются критическими.

На нашем  рисунке это точки Х₂, Х₃, Х₄, Х_5, Х₆ и Х₇.  Среди этих точек могут быть точки максимума ( max ) и  минимума ( min ), которые называются точками экстремума       ( X_max и X_min ).  Значения функции в этих точках называют экстремумами функции   и обозначают f_max (X_max)  и  f_min (X_min). 

Необходимым условием существования экстремумов является равенство нулю производной или если производная не существует, то есть необходимое условие – это наличие критических точек. (Это теорема Ферма), но этого условия еще не достаточно. Чтобы функция имела экстремум в некоторой точке, надо, чтобы при переходе через эту точку производная меняла свой знак, то есть надо, чтобы возрастание менялось на убывание, или убывание на возрастание. Если такой смены нет, то в этой критической точке не будет экстремума.

Если знак производной меняется с  (+ ) на (- ) – это точка max, если знак производной меняется с  (- ) на (+ ) – это точка min.

На рис.1:  Точка Х₂ является точкой max, т.к. при переходе через эту точку возрастание сменилось убыванием ( f ´(x) поменяла знак с  (+ ) на (- )). Такими же будут точки  Х₄   и Х_6.             В точках Х₃   и  Х₅   при переходе  f ´(x) поменяла знак с  (- ) на (+ ). Это точки min.

В  критической точке Х₇  не произошло смены знака производной (функция возрастала до этой точке и возрастает после этой точки). Здесь никакого экстремума нет. Это  точка перегиба. Не будет существовать экстремумов и в точках, в которых график функции будут разрываться. На нашем рисунке такого случая нет.

Вывод. Для существования экстремумов необходимо выполнение двух условий:

1.       Существование критических точек.

2.       Смена знака производной при переходе через критическую точку.

Ответить на вопросы.

Нахождение экстремумов функции осуществляют по следующему плану:

1.      Найти область определения функции.

2.      Найти производную.

3.      Найти критические точки ( приравнять производную к нулю).

4.      На числовой прямой отметить найденные критические точки, выделить            полученные числовые промежутки и проверить знак производной в каждом из них.

5.      Записать, где получились точки максимума или минимума, (а может быть и перегиба, если знак производной не менялся при переходе через точку, или разрыва).

6.      Вычислить значение  экстремумов функции (значение самой функции в точках экстремума.

7.      Для наглядности или когда надо построить график заданной функции, заносятся все полученные данные в таблицу.

Рассмотрим примеры.

Пример 1. Найти критические точки функции f(x) =x³ -7x² -5x +6 (в ответ записать большее значение).          Решение.

(В данном примере надо выполнить только три первых пункта плана.)

1.      D( f ) = (- ∞; + ∞).

2.      Найдем производную f ´(x) =(x³ -7x² -5x +6)´ =3х² – 14х -5

3.      3х² – 14х -5= 0      D= (-14)² - 4·3·(-5) = 196 + 60 = 256 = 16²

X₁ = (14+16)/(2·3) = 5      X₂ = (14 - 16)/(2·3) = - 1/3     Ответ: 5

Пример 2. Исследовать функцию f(x) =2x³  - 24x на экстремумы ( сделать таблицу, в ответ записать а) точку минимума; б) максимум функции).  

 Решение.

(В этом задании надо выполнить все пункты плана.)

1.      D( f ) = (- ∞; + ∞).

2.      Найдем производную f ´(x) =(2x³ - 24x)´= 6х² – 24

3.       6х² – 24=0 Здесь неполное квадратное уравнение, вынесем за скобки общий множитель  6 (х² – 4)=0;    х² – 4=0;     х² = 4;     х₁ =2 и х₂= - 2  это критические точки.   

4.        Знаки в промежутках определяют,  выбирая любые числа из каждого промежутка и подставляя в производную. Например, из промежутка ( -∞; -2) можно взять число         х= - 3.        6· (-3)² -24 = 6· 9 -24=30 > 0  (если квадратичная функция, знаки чередуются).       

5.            Xmax = -2     Xmin = 2

   6. f_max (-2) =2·(-2)³  - 24·(-2)=32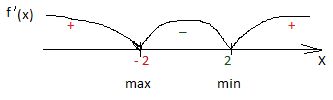  

      f_min (2) =2·(2)³  - 24·(2)= - 32

7.

Ответ:   а)  2               б)  32.

Пример 3. Исследовать функцию f(x) = Х +(1/х) на экстремумы ( сделать таблицу, в ответ записать  а) критические точки; б)  точку максимума; в) минимум функции).

Решение.

(В этом задании надо выполнить все пункты плана.)

1.      D( f ) = (- ∞; 0)  U (0; + ∞).      ( так как  в выражении 1/х   х≠0)

2.      Найдем производную f ´(x) =( Х +(1/х))´= 1 - (1 / х²) = (х² -1) / х²   

3.       (х² -1) = 0     х² =1      x₁ = -1   x₂ =1  при х=0 производная не существует.   Критических точек 3. Это  -1; 0; 1.                               

4.          

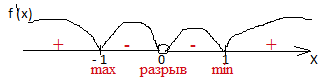Здесь функция не квадратичная функция и знаки надо проверять в каждом  промежутке.  Например, из промежутке   ( -1; 0) можно взять х= - 0,5.    1 - (1 / х²) = 1 – (1 /( - 0,5)²) = 1 –( 1/0,25)=  1 – 16 =-15 <0 ( поставили на рисунке знак минус.). Так проверяем знак в каждом промежутке в этом задании.

5. В этом примере две точки экстремума   Xmax = -1     Xmin = 1

6. f_max (-1) =  -1 +(1/-1)= -2

      f_min (1) = 1 +(1/1) = 2

7.

Ответ:  а)  -1;  0;  1.          б)  - 1.         в)  2.

Решить самостоятельно.

1.     Найти критические точки функции f(x) = -2x³ +6x² + 48x - 16 (в ответ записать меньшее значение).  

2.     Исследовать функцию f(x) =x³ - 27x + 20 на экстремумы ( без таблицы, в ответ записать а) точку минимума; б) минимум функции).  

3.      Исследовать функцию f(x) =3x⁴ - 4x³ + 5 на экстремумы ( сделать таблицу, в ответ записать  а) наименьшую критическую точку; б) точку экстремума; в) экстремум функции; г) что происходит с функцией в критической точке х=0 ?).  

Ответы на вопросы.

1.    Производная равна нулю или не существует.

2.    Точки минимума и максимума.

3.    Значение функции в точках экстремума.

4.    Максимум функции и минимум функции.

5.    Существование критических точек.

6.    Смена знака производной в этой точке.

7.    Максимум, если знак меняется с ( + ) на ( - ).

8.    Минимум, если знак меняется с ( - ) на ( + ).

Ответы на задачи.

1.    Критические точки   х= -2 и х=4;      меньшее  -2

2.      а) Точка минимума х=  3

б)  минимум функции f(x) =  -34

3.    а) наименьшая критическая точка х = 0

б)  точка экстремума    х=1

в) экстремум функции    f(1) = -1

г) что происходит с функцией в т. х=0?   Перегиб графика.