Исследование функций на монотонность.

Применение производной.

Исследование функции на возрастание и убывание (на монотонность).

Краткая теория.     (Теория и разобранные примеры должны быть записаны в тетрадь).

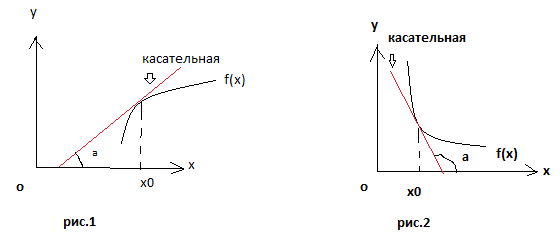
На рис.1 угол наклона касательной с положительным направлением оси ОХ – острый, а на рис.2 этот угол тупой. Если угол наклона  касательной острый, это означает, что производная в этой точке положительна, и функция при увеличении значения переменной Х  будет возрастать.( см. рис.1). Если  угол наклона касательной тупой, как на рис.2, это означает, что производная в это точке отрицательна, и функция на этом участке убывает. ( см.рис. 2.).     Итак,  условие возрастания и убывания функции:

У функции может быть несколько участков убывания и возрастания.   Рис. 3.Разберем пример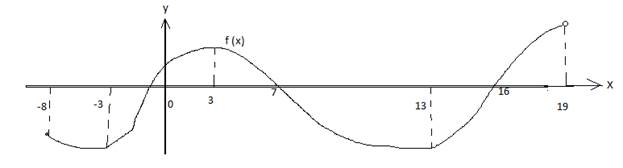На рис.3 изображен график некоторой функции f (x). Функция возрастает на промежутках          [-3;3]  и [13;19). На этих промежутках угол наклона касательной с положительным направлением оси ОХ  острый, значит производная f  ´(x)  > 0, так как тангенс острого угла положителен.  Функция убывает на   промежутках [ -8; -3] и [3;13], так как на этих участках угол наклона касательной с положительным направлением оси ОХ  тупой, значит производная f  ´(x)  < 0, так как тангенс тупого  угла отрицательный.                                                                        Если надо определить участки возрастания и убывания не по графику, а путем вычислений, то действуют по такому плану:                                                                                                                       1. Найти область определения заданной функции.

2. Найти производную  f  ´(x)  заданной функции.

3. Найти промежутки, где производная f  ´(x)  > 0  и f  ´(x)  < 0, ( решая полученные неравенства аналитически или методом интервалов).

Пример1.  Исследовать функцию f(x) = 5x² -3x +1 на монотонность (на возрастание и убывание).                                 Решение.

1.       Область определения функции   D(f) = R.

2.       f ´(x) = (5x² -3x +1)´ = 10x – 3   

3.       f ´(x) = 0     10x -3 =0    10x=3       x= 0,3         Отметим  найденную точку на числовой прямой. Числовая прямая разбилась на два промежутка  (-∞; 0,3] и [0,3; + ∞). Проверим знак производной в каждом из полученных промежутков. Для этого выбираем любое произвольное число из левого промежутка и потом из правого. Выберем любое число         х < 0,3 например, х= 0 и подставим вместо х в производную, получим:  10·0 -3= -3 < 0. Поставим слева от числа 0,3  знак минус на числовой прямой. Выберем любое число           х > 0,3 например, х=2 и подставим вместо х в производную, получим:  10·2 -3= 17>0. Поставим  справа от числа 0,3 знак плюс на числовой прямой.  Там, где производная положительна  (  f ´(x) >0) функция возрастает, то есть возрастает  на промежутке                [ 0,3; +∞)                              

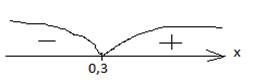                          Там, где  производная отрицательна 

(  f ´(x)< 0) функция убывает, то есть убывает на ( -∞; 0,3].

Пример2.  Исследовать функцию f(x) = 3x² –2x³ +12х    на возрстание и убывание. Найти длину участка возрастания.

1.   Область определения функции   D(f) = R.

2. f ´(x) = (3x² -2x³ +12х)´= 6х – 6х² +12

3. f ´(x) = 0     6х – 6х² +12 =0  разделим на 6 и перепишем по порядку.     - х² +х +2 = 0  Решим это квадратное уравнение, найдем дискриминант и корни.

D= 1² - 4·(-1)·2 = 1 + 8 = 9>0  - два корня. X₁ = ( - 1+√9) / ( -2) =2/ (-2)= - 1;  X₂ = ( - 1-√9) / ( -2) =2

 Отметим  найденные точки на числовой прямой. Числовая прямая разбилась на три промежутка:

(-∞; -1] , [-1; 2 ]  и [2; +∞). Прверим знак производной в каждом промежутке.  На (-∞; -1] выберем, например, х = -3 и подставим в производную.  . f ´(-3)=  - ( -3)² +(-3) +2= -9 -3 +2 = -10<0

В случае, когда производная получилась в виде квадратичной функции, то знак в каждом промежутке проверять не надо, достаточно определить знак в одном промежутке, в остальных знаки будут обязательно чередоваться. Изобразим числовую прямую и расставим знаки производной.

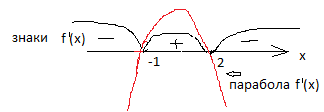
Производная положительна на [-1; 2] , значит на этом промежутке функция возрастает. Производная отрицательна на промежутках (-∞; - 1]  и [2; +∞), значит функция убывает на этих промежутках.  Найдем длину участка возрастания    2 – (-1) = 2 +1 =3.   Ответ: функция возрастает на промежутке[-1; 2] , убывает на промежутках  (-∞; - 1]  и [2; +∞). Длина участка   3.                                                                                                                             Решить самостоятельно.

Задача1.  Исследовать функцию f(x) = 5x² -3x +1 на монотонность (на возрастание и убывание).

   Задача2.     Исследовать функцию f(x) = - 3x² + x³ - 24х +1   на возрстание и убывание. Найти длину участка убывания.

     Задача3.     По графику функции ответить на вопросы.

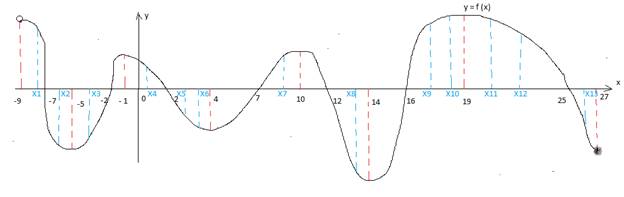
1.       а) Количество участков возрастания.  б) Перечислить участки по рисунку.

2.       а) Количество участков убывания.  б) Перечислить участки по рисунку.

3.       а) Сколько точек, где производная равно нулю. б) Перечислить эти точки. (Конечные точки графика не учитываются, в этих точках нельзя провести касательные к графику, так как нет окрестности  слева или справа). Касательная к графику в этих точках должна быть параллельна оси ОХ. (Например, Х=4 или Х=10 и т.д.)

4.       В каких точках  Х₁, Х₂,…,Х₁₃     производная положительна.  [ Если  f  ´(x)  > 0  на некотором  промежутке, то функция возрастает на этом промежутке] , Значит эти точки надо искать на участках возрастания. а) количество точек, б) перечислить точки.

5.       В каких точках  Х₁, Х₂,…,Х₁₃     отрицательна.  [ Если  f  ´(x)  < 0  на некотором  промежутке, то функция убывает  на этом промежутке] , Значит эти точки надо искать на участках убывания. а) количество точек, б) перечислить точки.

6.       Найти длину наименьшего участка возрастания.

7.       Найти длину наибольшего участка убывания.

Ответы на задачи.

Задача 1.    Функция возрастает для х ϵ ( - ∞; 0,25],

Функция убывает для х ϵ  [0,25 ; +∞)

Задача 2.     Функция возрастает для х ϵ( - ∞; - 2] и , [4 ; +∞)

Функция убывает для х ϵ [- 2 ; 4 ].

Длина участка убывания равна 6.

Задача3.     

1.    а ) 3   б) [-5; -1] , [4;10], [14 ;19]

2.    а ) 4   б) (-9; -5] , [-1 ;4], [10 ;14] ,[19 ;27]

3.     6:     х=-5,  х= -1, х=4, х=10, х=14. х=19.

4.    4 точки:    х₃,  х₇, х₉,  х_{10 .}

5.    9 точек:   х₁, х₂, х₄, х₅, х₆, х₈, х₁₁, х₁₂, х₁₃.

6.    Длина наименьшего участка возрастания ( их длины 4,6,5) наименьшего  4

7.    Длина наибольшего  участка убывания (их длины 4,5,4,8)  наибольшего 8.

8.