Исследовательская работа «3Д геометрия на примере элементов магнитного конструктора»

VIII Муниципальная научно-практическая конференция

«ПЕРВЫЕ ШАГИ В НАУКУ»

 

 

 

 

 

 

 

Исследовательская работа

«3Д геометрия на примере

элементов магнитного конструктора»

 

 

 

 

 

Выполнил:

Лимин Владимир,

ученик 3 класса МБОУ «Леплейская СОШ»

Руководитель:

учитель математики и

информатики МБОУ «Леплейская СОШ» Лимина Н.В.  

 

 

 

2023

Оглавление

 

Введение………………………………………………………………………..….3

1.       Что такое геометрия..........................................................................................5

2.       Правильные многогранники…….………………………………………........8

3.       Магнитный конструктор как средство создания и представления правильных многогранников……………………………………………….…….9

Заключение……………………………………………………………………….14

Список использованной литературы…………………………………….……..16

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

 

Геометрия в своей сущности и есть такое соединение живого воображения и строгой логики, в котором они взаимно организуют и направляют друг друга.

А.Д. Александров.

Геометрия – один из важнейших разделов математики, без которого не мыслимы как сама математика, так и современные естествознание и техника. Геометрическое решение задач, как правило, отличается наглядностью и делает полученные результаты более прозрачными и доступными пониманию. Эту же цель преследует графическое (т.е. использующее геометрические образы) представление информации, которое успешно осуществляют современные компьютеры.

Знание геометрии необходимо современному специалисту,  а также будущим специалистам – студентам и школьникам – не только потому, что эти знания вооружают их мощными средствами для решения практических и научных задач, но также потому, что они формируют мировоззрение человека, его представления об окружающем его пространстве.

С первого класса на уроках математики учеников знакомят с различными геометрическими фигурами, телами и поверхностями. Это позволяет видеть их в каждом предмете. Геометрические 3Д модели окружают каждого человека в повседневной жизни, но не все люди умеют правильно их представлять в пространстве.

Элементы магнитного конструктора позволяют формировать правильные многогранники, поэтому цель исследовательской работы: использование элементов магнитного конструктора для восприятия и изучения правильных многогранников.

Для достижения данной цели были поставлены следующие задачи:

1.     Изучить информационные источники по проблеме исследовательской работы.

2.     Выяснить, что такое геометрия.

3.     Выяснить, какие виды правильных многогранников существуют.

4.     Создать правильные многогранники при помощи элементов магнитного конструктора.

В исследовании была выдвинута гипотеза, что исследование правильных многогранников позволят развивать не только математические и логические навыки, но оттачивает ассоциативное, пространственное и образное мышление при помощи использования элементов магнитного конструктора.

Актуальность исследования заключается в том, что уже с рождения все мы видим вокруг различные многогранники, поэтому необходимо уметь их правильно распознавать и представлять.

Объект исследования: раздел математики – геометрия

Предмет исследования: правильные многогранники.

Методы исследования: обзор литературы, опрос, самостоятельная исследовательская работа, формулирование выводов, оформление работы, сравнение, обобщение.

 

 

 

 

 

 

 

 

 

 

1.     Что такое геометрия

 

Геометрия – один из самых увлекательных и важных разделов математики. Именно она знакомит с разнообразием пространственных форм, формирует необходимые пространственные представления, дает метод научного познания, способствует развитию логического мышления. Кроме этого, изучение геометрии способствует приобретению необходимых практических навыков в изображении, моделировании и конструировании пространственных фигур, в измерении основных геометрических величин (длин, углов, площадей, объемов).

Геометрия имеет яркую историю, связанную с именами знаменитых ученых:  Пифагора,  Евклида,  Архимеда,  Фалеса,  И. Кеплера,  Р. Декарта, Л. Эйлера, Н. И. Лобачевского и др.

Она возникла и развивалась в связи с потребностями практической деятельности человека. С древних времен люди сталкивались с необходимостью находить расстояния между предметами, определять размеры участков земли, ориентироваться по расположению звезд на небе и т.п.

Слово геометрия – греческое, оно означает «Землемерие» (гео – земля, метрео – измеряю).

О зарождении геометрии в Древнем Египте около 2000 лет до нашей эры древнегреческий ученый Геродот (V в. До н. э.) написал следующее: «Сеозоострис, египетский фараон, разделил землю, дав каждому египтянину участок по жребию, и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию».

При строительстве различных различных сооружений необходимо было расчитывать, сколько материала пойдет на постройку, вычислять расстояния между точками в пространстве и углы между прямыми и плоскостями, знать свойства простейших геометрических фигур. Так, египетские пирамиды, сооруженные за две, три и четыре тысячи лет до нашей эры, поражают точностью своих метрических соотношений, свидетельствующих, что их строители уже знали многие геометрические положения и расчеты. Они состоят из каменных блоков, весом 15 тонн и эти "кирпичики" так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы - рычаги и катки. "Все боится времени, но само время боится пирамид".

Ученые и философы Древней Греции восприняли и переработали достижения культуры и науки Древнего Востока, Фалес, Пифагор, Демокрит, Евдокс и др. ездили в Египет и Вавилон для изучения музыки, математики и астрономии. Не случайно зачатки греческой геометрической науки связаны с именем Фалеса Милетского, основателя ионийской школы. Ионийцы, населявшие территорию, которая граничила с восточными странами, первыми заимствовали знания Востока и стали их развивать.

Одной из первых школ была ионийская. Её основателем считаются Фалес Милетский. Он мог находить высоту предмета по его тени, пользуясь тем, что треугольник определяется одной стороной и двумя прилежащими к ней углами. Фалес измерил высоту пирамиды, " наблюдая тень пирамиды в тот момент, когда наша тень имеет такую же длину, как и мы сами". Он считал, что отношение высоты вертикально поставленной палки к длине её тени равно отношению высоты пирамиды к длине её тени.

Таким образом, Фалесу приписывают теорему о том, что равноугольные треугольники имеют пропорциональные стороны.

Начиная с VII века до нашей эры, в Древней Греции создаются так называемые философские школы, в которых происходит постепенный переход от практической к теоретической геометрии. Все большее значение в этих школах приобретают рассуждения, с помощью которых удавалось получать новые геометрические свойства, исходя из некоторого перечня свойств, принимаемых без доказательства и называемых аксиомами.

Одной из самых первых и самых известных школ была пифагорейская (VI-V вв. до н. э.), названная так в честь своего основателя Пифагора.

Объяснение устройства мира пифагорейцы тесно связывали с геометрией. Так, выделяя первоосновы бытия, они приписывали их атомам форму правильных многогранников, а именно: атомам огня – форму тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. Всей Вселенной приписывалась форма додекаэдра, воды – икосаэдра. Всей Вселенной приписывалась форма додекаэдра.

Более поздняя философская школа – Александрийская – интересна тем, что дала миру знаменитого ученого Евклида, который жил примерно в 300 г. до нашей эры. Насколько серьезно и строго он относился к изучению математики, можно судить по следующему известному рассказу. Царь Птолемей спросил у Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его «Начала». Евклид на это ответи: «В геометрии нет царского пути».  Именнов в этом труде впервые было представлено стройное аксиоматическое строение геометрии. На протяжении около двух тысячелетий этот труд остается основой изучения системтичекого курса геометрии.

Вслед за Евклидом Архимед занимался изучением правильных многогранников. Убедившись в том, что правильных многогранников только пять, Архимед стал строить многогранники, у которых гранями являются правильные, но не одноименные многоугольники, а в каждой вершине, как и у правильных многогранников, сходится одно и то же число рёбер. В результате были получены так называемые равноугольно полуправильные многогранники. До нас дошла работа ученого, которая называется «О многогранниках», подробно описывающая тринадцать таких многогранников, получивших название « тела Архимеда».

В последние столетия возникли и развивались новые направления геометрии, среди которых: геометрия Лобаческого, топология, теория графов и др. Появились новые методы, в том числе координатный и векторный, позволяющие переводить геометрические задачи на язык алгебры и наоборот. Геометрия широко используется в ругих науках: физике, химии, биологии, экономике и др.

В 1877 году немецкий математик Феликс Клейн в своей «Эрлангерской программе» предложил классификацию различных разделов геометрии, которая используется и в наши дни: евклидова геометрия, проективная, аффинная, начертательная, многомерная, неевклидова геометрии, геометрия многообразий, топология.

Евклидова геометрия состоит из двух частей: планиметрии и стереометрии.

Планиметрия – это раздел геометрии, в котором изучаются геометрические фигуры на плоскости.

Стереометрия – это раздел геометрии, в котором изучаются фигуры в пространстве.

Проективная геометрия изучает свойства фигур, которые сохраняются при их проецировании (замене на подобные фигуры другого размера).

Аффинная геометрия исследует постоянные свойства фигур при различных изменениях плоскости и пространства.

Инженерная дисциплина – начертательная геометрия использует для изображения предмета несколько проекций, что позволяет делать трёхмерное изображение объекта.

Многомерная геометрия исследует альтернативное существование четвертого измерения.

Отдельно выделяют инструментальные подразделы: аналитическую геометрию, которая для описания геометрических фигур использует алгебраические методы и дифференциальную геометрию, которая изучает графики различных функций.

2.     Правильные многогранники

 

Правильные многогранники интересовали многих великих учёных. И этот интерес выходил далеко за пределы математики. Платон (427 до н.э. –

 347 до н.э.) рассматривал их как основу строения Вселенной, Кеплер (1571—1630) пытался связать правильные многогранники с движением планет Солнечной системы (которых в его время было известно пять). Возможно, именно красота и гармония правильных многогранников заставляла великих учёных прошлого предполагать какое-то более глубокое их назначение, чем просто геометрических объектов.

Правильным многогранником называется многогранник, все грани которого есть правильные многоугольники, все плоские углы которого равны между собой и двугранные углы которого равны между собой. (Плоскими углами многогранника называются углы многоугольников-граней, двугранными углами многогранника называются углы между гранями, имеющими общее ребро.)

В трёхмерном пространстве существует ровно пять правильных многогранников: тетраэдр, октаэдр, куб (гексаэдр), икосаэдр, додекаэдр.

 

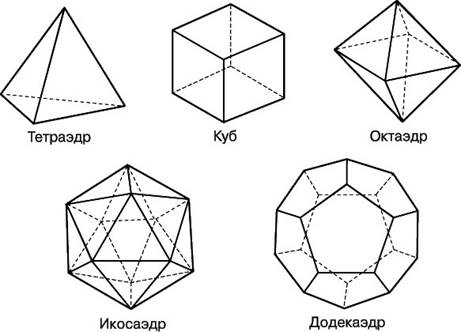
Рис. 1 Правильные многогранники

 

То, что других правильных многогранников не существует, было доказано Евклидом (около 300 г. до н.э.) в его великих Началах.

Тетраэдром (от греч. τετρά, в сложных словах – четыре и έδρα – грань) называется правильный многогранник, имеющий 4 треугольные грани. У него 4 вершины, 6 рёбер.

Октаэдр (от греч. Οκτώ – восемь). Октаэдр имеет 8 треугольных граней, 6 вершин, 12 рёбер.

Куб или гексаэдр (от греч. Εξά – шесть). У куба грани являются квадратами. Он имеет 6 граней, 8 вершин, 12 рёбер.

Икосаэдр (от греч. Είκοσι – двадцать) – это правильный многогранник, у которого 20 треугольных граней. Он имеет 12 вершин, 30 рёбер.

Додекаэдр (от греч. Δώδεκα – двенадцать). Грани додекаэдра – правильные пятиугольники. У додекаэдра 12 граней, 20 вершин, 30 рёбер.

 

3.     Магнитный конструктор как средство создания и представления правильных многогранников

 

Магнитный конструктор - это развивающий конструктор нового поколения. Он состоит из деталей, представляющих собой простые геометрические фигуры: треугольники, квадраты, прямоугольники, ромбы, пятиугольники, шестиугольники, трапеции  и другие, которые легко соединяются между собой силой магнитного притяжения.

Магниты находятся внутри очень прочного многослойного пластикового корпуса, поэтому они ни при каких обстоятельствах не могут выпасть. Зато магниты свободно вращаются внутри, всегда, поворачиваясь, друг к другу нужным полюсом. Таким образом, все детали конструктора всегда притягиваются.

Рис 2. Элементы магнитного конструктора

Неодимовые магниты в 8 раз сильнее обычных. Этой силы хватает, чтобы создавать большие уникальные постройки.

Элементы магнитного конструктора легко знакомят с объёмными фигурами, развивают пространственное и абстрактное мышление, знакомят с азами арифметики и геометрии, погружают в увлекательный мир 3D-моделирования. Для школьников это уже серьёзный помощник в изучении геометрии.

С помощью элементов магнитного конструктора удалось создать тетраэдр, гексаэдр (куб), октаэдр и икосаэдр.

В силу отсутствия 12 пятиугольников, додекаэдр построить не удалось.

 

                                                             Рис 3. Тетраэдр

 

Рис 4. Гексаэдр (куб)

 

Рис 5. Октаэдр

Рис 6. Икосаэдр

Была показана демонстрация полученных многогранников в 5 классе, одноклассники просили попробовать самостоятельно создать их, это вызвало интерес и побудило их к изучению элементов геометрии. Также был  записан видеоролик, в котором отражен мастер-класс по созданию данных многогранников, который можно просмотреть, перейдя по ссылке https://youtu.be/oAZVi4QpjeE.

 

 

 

 

 

 

 

 

 

 

 

Заключение

 

Наука геометрия очень важна для человека. Геометрия развивалась за несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции. Сегодня уже в начале XXI столетия мы можем повторить восклицание архитектора Корбюзье с ещё большим изумлением.  В самом деле, посмотрите вокруг - всюду геометрия! Современные здания и космические станции, подводные лодки, интерьеры квартир и бытовая техника – всё имеет геометрическую форму. Геометрические знания являются сегодня профессионально значимыми для многих современных специальностей: для дизайнеров и конструкторов, для рабочих и учёных. И уже этого достаточно, чтобы ответить на вопрос: «Нужно ли нам Геометрия?» 

Во-первых, геометрия является первичным видом интеллектуальной деятельности, как для всего человечества, так и для отдельного человека. Мировая наука началась с геометрии. Ребёнок, ещё не научившийся говорить, познаёт геометрические свойства окружающего мира.  Во-вторых, геометрия является одной из составляющей общечеловеческой культуры. Человек не может по-настоящему развиться культурно и духовно, если он не изучал в школе геометрию; геометрия возникла не только из практических, но и из духовных потребностей человека. Итак, геометрия – один из важнейших предметов в школе. Я отметил, что в нашей жизни мы часто встречаем геометрические тела и фигуры. Из них состоят все предметы, которые нас окружают, начиная с тарелки, с которой едим, и заканчивая телевизионной тарелкой, которая передает программы со всего мира. В квартирах, домах нас окружают геометрические фигуры: отрезки, квадраты, прямоугольники, круги, окружности, кубы и прямоугольные параллелепипеды. А также предметы, состоящие из сочетания этих геометрических фигур. Необходимо уметь строить все эти геометрические фигуры на листе бумаги, для изготовления чертежа или схемы. Но для начала надо иметь пространственное представление о геометрических фигурах, а это нужно развивать.

Разнообразие формы и цвета нам подарила родная планета! А геометрия - это наука о форме предмета… 

Значимость работы заключается в том, что многие ученики, познакомившись с данным исследованием, на вопрос о необходимости изучать геометрию - ответят положительно! И, конечно же, будут с интересом изучать сложную, но увлекательную науку – геометрию!  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список литературы

 

1.       Смирнов В.А., Смирнова И.М., Ященко И.В. Наглядная геометрия. – М.: МЦНМО, 2013.

2.       Гусев В.А., Кожухов И.Б., Прокофьев А.А. Геометрия. Полный справочник. – М.: Махаон, 2006.

3.       Математический энциклопедический словарь. Гл.ред. Ю.В. Прохоров. – Сов. Энциклопедия, 1988

4.       Энциклопедический словарь юного натуралиста/Сост. А.Г. рогожкин-1981

5.       Занимательная геометрия/ К.И. Шевелёв – М.:Ювента,2009

6.       Г. С. М. Кокстер. Введение в геометрию. – М.: Наука, 1966.

7.       Ж. Адамар. Элементарная геометрия. Ч. 2. Стереометрия. – М.: Просвещение, 1951.

8.       Евклид. Начала Евклида. Книги XXI–XXV. – М.: – Л.: ГИТТЛ, 1950.

9.       Гончар В.В. Модели многогранников. – Ростов-на-Дону: Феникс, 2010.

 

 

Скачано с www.znanio.ru