Исследовательская работа ФУНКЦИЯ В НАШЕЙ ЖИЗНИ 10 класс

XVIII Малая академия наук юных исследователей

 

 

«Математика»

 

 

 

 

 

Исследовательская работа

 

 

 «ФУНКЦИЯ В НАШЕЙ ЖИЗНИ»

                                                                                               

 

 

 

 

 

Автор работы:

Сандукова Валерия

10 класс,

МБОУ Позднеевская СОШ

 

 

 

 

 

 

 

Руководитель:

Кривопустова Мария Николаевна,

учитель математики,

МБОУ Позднеевская СОШ

 

 

 

 

 

 

 

 

 

 

2020 год

ОГЛАВЛЕНИЕ

 

Введение

История развития понятия функции

Понятие функции, виды функций, применение функций и графиков функций

1.Основные понятия

2. Линейная функция

3. Квадратичная функция

4. Степенная функция

5. Показательная функция

6. Логарифмическая функция

7. Тригонометрическая функция

8. Функции и графики в нашей жизни

Заключение

Приложение: Результаты исследования гибкости среди обучающихся Позднеевской СОШ

Список литературы

 

 

 

 

 

 

ВВЕДЕНИЕ

 

«Именно функция является тем средством математического языка,

которое позволяет описывать процессы движения,

изменения ,присущие природе»

Галилео Галилей

Математика – один из моих самых любимых предметов. Я считаю, что ни одно явление, ни один процесс в окружающем мире не могут быть изучены без математического описания. Одним из инструментов описания реального мира является функция.

Современная математика знает множество функций, и у каждой своей неповторимый облик, как неповторим облик каждого из миллиардов людей, живущих на земле.

Мы тоже являемся функцией многих переменных, одна из которых – время. Проходят годы и мы меняемся. Мы также зависим от своей наследственности, от книг, которые мы читаем, от температуры окружающей нас среды и от многих других факторов.

Однако при всей непохожести одного человека на другого у каждого есть руки и голова, уши и рот.

Точно так же облик каждой функции можно представить сложенным из набора характерных деталей. В них появляются основные свойства функций.

На уроках математики все знакомятся с различными функциями, их свойствами и графиками, но мало знают о том, где в реальной жизни можно встретиться с этой моделью, и как человек использует свойства функций в своей практической деятельности.

На уроках математики мы познакомились с различными функциями, их свойствами и графиками, но мы мало знаем о том, где в реальной жизни можно встретиться с этой моделью, и как человек использует свойства функций в своей практической деятельности.

Цель:

Изучить и исследовать связь функций с явлениями окружающего мира и практической деятельностью человека.

Задачи:

1.Выявить связь функций с явлениями окружающего мира и практической деятельностью человека.

2.Показать, что функции находят широкое применение в жизни и в математике. что одним из инструментов описания реального мира является функция.

3.Рассмотреть пример использования функции при сдаче норм ГТО обучающимися нашей школы

 

 

ИСТОРИЯ РАЗВИТИЯ ПОНЯТИЯ ФУНКЦИИ

 

Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Идея функциональной зависимости восходит к древности. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r2. Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы.

Кроме того, у Декарта и Ферма (1601-1665) в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в «флюентой»).

В «Геометрии» Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость - функция от времени (t) и т.п.

Само слово «функция» (от латинского functio - совершение, выполнение) впервые было употреблено немецким математиком Лейбницем  в 1673г. Швейцарский математик Иоганн Бернулли (1667-1748), который в 1718 году определил функцию следующим образом: «функцией переменной величины называют количество, образованное каким угодно способ из этой переменной величины и постоянных». Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во «Введении в анализ бесконечного»). Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье (1768-1830), занимавшийся в основном математической физикой.

        Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С.Л. Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенной функции внести ученики и последователи Шварца - И.М. Гельфанд, Г.Е. Шилов и др.

 

ПОНЯТИЕ ФУНКЦИИ, ВИДЫ ФУНКЦИЙ, ПРИМЕНЕНИЕ ФУНКЦИЙ И ГРАФИКОВ ФУНКЦИЙ

 

1.Основные понятия

Что же такое функция?

Разные ученые выдвигали разные мысли. Но я хочу вас познакомить с одним определением: «Если даны числовое множество X и правило f, позволяющие поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у = f(x) с областью определения Х; у = f(x) , хЄХ. При этом переменную х называют независимой переменной или аргумент, а переменную у- зависимой переменной.»

Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Функция – это не только математическое понятие, но и:

функция — работа, производимая органом, организмом; роль, значение чего-либо;

функция в математике — закон зависимости одной величины от другой;

функция — возможность, опция, умение программы или прибора;

функция — обязанность, круг деятельности;

функция персонажа в литературном произведении;

функция — вид подпрограммы в информатике социальная функция.

Каждая область знаний: физика, химия, биология, социология, лингвистика имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов.

В различных науках и областях человеческой деятельности возникают количественные соотношения, и математика изучает их в виде свойств чисел.

Математика создает условия для развития умения применять теоретические знания для решения практических задач, ориентироваться в окружающей нас действительности. Нам кажется, что функциональные зависимости могут касаться самых разнообразных явлений природы и окружающей среды. Каждому человеку в его повседневной практической деятельности приходится применять практические приемы геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков. Без конкретных математических знаний затруднено понимание и восприятие научных знаний, разнообразной социальной, экономической, технологической информации.

Свободное владение техникой построения графиков часто помогает решать многие задачи, а порой является естественным средством их решения. Математика является языком различных областей науки и нашей жизни.

Экологические проблемы являются глобальными проблемами человечества, всех стран независимо от размеров территории, численности населения, уровня экономического развития.

 

 

 

2.Линейная функция

 

Линейная функция — функция вида y = kx + b (для функций одной переменной).

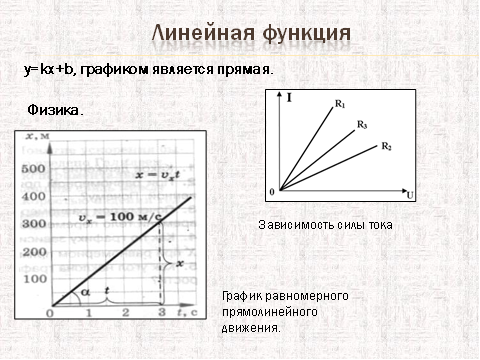
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности. График линейной функции является прямая линия, с чем и связано ее название. Во многих сферах деятельности человека встречаются процессы, которые можно описать с помощью линейной функции.

Пример из физики. Велосипедист движется со скоростью 10км/ч. Записать формулу его пути S за время движения t. Построить график движения на первых тридцати километрах пути.

Пример из метеорологии. При начале нагревания вода в кипятильнике имела температуру 60C. При нагревании температура воды повышалась каждую минуту на 20 C. Найдите формулу, выражающую изменение температуры T воды в зависимости от времени t её нагревания. Будет ли функция T(t) линейной?

Пример из геометрии. Одна сторона прямоугольной детской площадки равна X, другая – на 3 м больше. Выразите через X периметр P и площадь S этого прямоугольника. Найдите значение каждой функции P(X) и S(X) при X=6. При каком значении X периметр будет равен 46 м.

Пример из экономики. На складе было 300 т угля. Ежедневно на склад привозили ещё по 40 т. Выразить формулой зависимость количества угля p (в тоннах), находящегося на складе, от времени (в днях). Итак, мы приходим к выводу: во многих сферах деятельности человека встречаются процессы, которые можно описать с помощью линейной функции.

 

3.Квадратичная функция

 

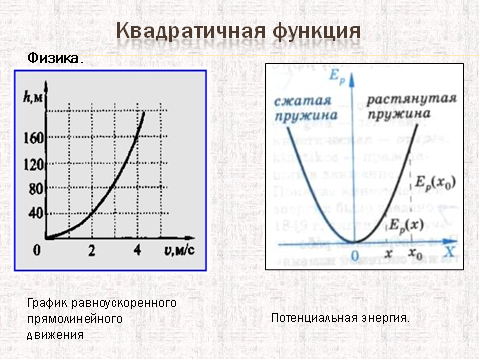
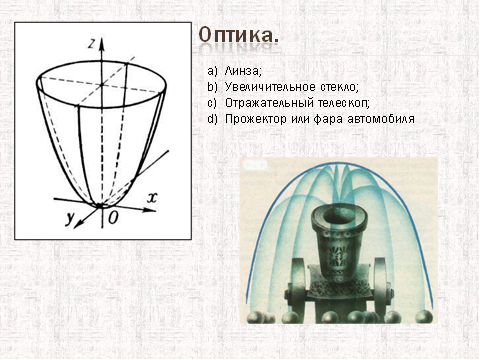
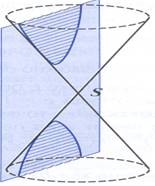Самые близкие родственники параболы – это окружность, гипербола и эллипс. А роднит все эти кривые обыкновенный конус: если провести плоскость, которая параллельна оси конуса, то линией пересечения окажется гипербола.

Слово «гипербола» по своему происхождению греческое (ὑπερβολή — избыток) был введён Аполлонием Пергским (ок. 262 год до н. э. — ок. 190 год до н. э.), поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Гипербола - это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.

 

 

 

 

 

 

 

 

 

 

 

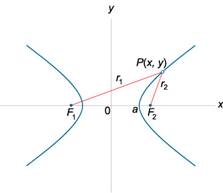
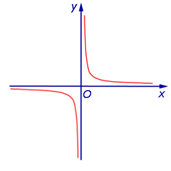
4.Степенная функция

Мы уже знакомились с функциями y = x, y = x2, y = х3, у = 1/х и т.д. Все эти функции являются частными случаями степенной функции, то есть функции y = xp , где p – заданное действительное число. Свойства и график степенной функции существенно зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень xp.

Рассмотрим, какие виды графиков может иметь степенная функция:

Посредством степенной функции f(x) = Ax описывается зависимость интенсивности основного обмена от веса животного. Здесь х – вес животного; f(x) – количество кислорода, поглощаемого животным в единицу времени; А и  – параметры, постоянные для данного класса живых существ. Для млекопитающих и птиц, например,  = 0,74, А = 70, для рыб  = 0,8, А = 0,3.

Замечательное свойство параболы широко используется в науке и технике. Известно также, что многие законы природы выражаются в виде квадратичной зависимости. Например, скорость воды в реке на разных глубинах разная: у дна и у поверхности наименьшая, где-то внутри потока она наибольшая. По данным некоторых исследователей можно считать, что если от оси OY отложить горизонтальные отрезки, равные по длине скорости воды на соответствующей глубине, то получится парабола с горизонтальной осью, вершина которой находится на 1/3 глубины потока.

 

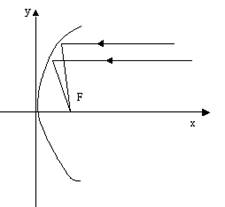
5.Показательная функция

На рисунке представлены графики этой функции. Мы знаете, еще 40 веков назад в египетском папирусе записан ряд. Про семь домов, где кошек 49, и каждая из них по 7 мышей съедает и тем всем столько зерен сохраняет, что мер 17000 составляет.

О том еще известна нам легенда, что как-то у арабского царя. Изобретатель шахматной доски, наверно потребовал за доску ту зерна. Причем за клетку первую – зерно, а за вторую – два просил изобретатель, за третью – снова больше раза в два, немало времени царь на подсчет потратил. Когда же подсчитали – прослезились: число двадцатизначно получилось! Хватило б зернами засеять нам всю сушу и миллионы лет пришлось зерно бы кушать.

Все знают, что такое ростовщик. Тот человек проценты брать привык. Они встречались в Вавилоне древнем, где пятую часть “лихвы” взимали в среднем!

Пятнадцатый век – рожденье банков, дающих деньги людям под процент, тогда и встал вопрос о дробном показателе. Его развили математик Штифель, Оресм, Шюке. Показательная функция, подобно линейной и квадратичной, очень часто реализуется в физических, биологических и иных законах. И это, конечно, не является случайностью. В жизни нередко приходится встречаться с такими фактами, когда скорость изменения какой-либо величины пропорциональна самой величине (размножение бактерий, ход химической реакции и т.д.). В этом случае рассматриваемая величина будет изменяться по закону, имеющему вид: y = y0ax.

По закону показательной функции размножалось бы все живое на Земле, если бы для этого имелись благоприятные условия, т. е. не было естественных врагов и было вдоволь пищи. Доказательство тому – распространение Австралии кроликов, которых там раньше не было. Достаточно было выпустить пару особей, как через некоторое время их потомство стало национальным бедствием.

Если бы все маковые зерна давали всходы, то через 5 лет число “потомков” одного растения равнялось бы 243 • 1015 или приблизительно 2000 растений на 1 м2 суши.

Потомство комнатных мух за лето только от одной самки может составить 8 • 1014. Эти мухи весили бы несколько миллионов тонн, а выстроенные в одну цепочку, они составили бы расстояние, большее, чем расстояние от Земли до Солнца. Потомство пары мух за 2 года имело бы массу, превышающую массу земного шара. И только благодаря сообществу животных и растений, когда увеличение одного вида влечет за собой рост количества его врагов, устанавливается динамическое равновесие в природе.

В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число раз, т. е. по закону показательной функции. Эти процессы называются процессами органического роста или органического затухания. Например, рост бактерий в идеальных условиях соответствует процессу органического роста; радиоактивный распад вещества – процессу органического затухания. Законам органического роста подчиняется рост вклада в Сберегательном банке, восстановление гемоглобина в крови, донора или раненого, потерявшего много крови, рост дрожжей, ферментов, микроорганизмов. Закон органического роста выражается формулой: N = N0ekt. По этому же закону изменяется количество древесины в дереве, что имеет большое значение для рационального ведения лесного хозяйства.

Радий распадается в зависимости от времени по закону М = М0 e-kt , где: М0 – начальное количество радия, k – некоторый коэффициент. Пользуясь этой формулой, ученые смогли подсчитать возраст Земли, то есть время, в течение которого радий смог распадаться нормально.

Все слышали о цепных реакциях, теорию которых в 20-х годах описал молодой химик Н.Н. Семенов, а потом развили ученые-атомщики. Как управлять этим процессов в мирных целях? На этот вопрос можно ответить только при помощи знаний о показательной функции. .

Давление атмосферы, выраженное в миллиметрах ртутного столба, меняется по закону:  , где h – высота точки над уровнем моря (в м). Эту формулу используют геодезисты для барометрического нивелирования, то есть для определения разности высот над уровнем моря двух точек на земной поверхности.

Многообразные применения показательной (или её ещё называют, экспоненциальной) функции вдохновили английского поэта Элмера  Брила на написание “Оды экспоненте”, отрывок из которой гласит:
“…Ею порождено многое из того, что “достойно упоминания”,
Как говорили наши англосаксонские предки. Могущество её порождений
Заранее обусловлено её собственной красотой и силой, Ибо они суть физическое воплощение абстрактной идеи. Английские моряки любят и знают её под именем “Гунтер”. Две шкалы Гунтера – вот чудо изобретательности.
Экспонентой порождена логарифмическая линейка:  Даже изящные искусства питаются ею. Разве музыкальная гамма не есть набор  логарифмов? И таким образом нечто абстрактно красивое стало предком одного из величайших человеческих достижений”.

 

6.Логарифмическая функция

Самая интересная, полезная и лирическая – это функция логарифмическая. Спросите вы: “А чем интересна?”. А тем, что она обратная  показательной и относительно прямой у = х, как известно, симметричны их графики.

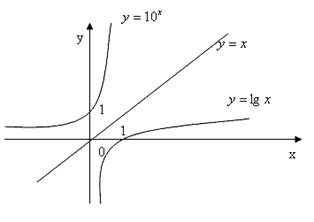
Проходит график через точку (1,0) и в том еще у графика соль, что в правой полуплоскости он “стелется”, а в левую попасть и не надеется.

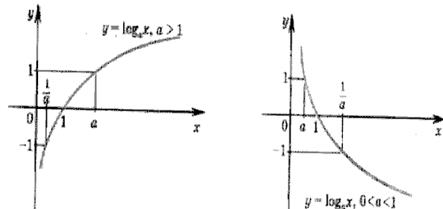
Функция порою убывает, порою по команде возрастает. 
А командиром служит ей значение а, и подчиняется она ему всегда.

Вот вы когда-нибудь слыхали о логарифмической спирали?

Закручены по ней рога козлов, ракушки моллюсков и улиток. И как сказал поэт  Гете: “Вы совершеннее строенья не найдете!” И эту спираль мы повсюду встречаем: к примеру, ножи в механизме вращаются по этой спирали. В подсолнухе семечки, паутина - это логарифмические спирали. Галактики тоже кружат по спирали! Музыка и звуки! Это все - логарифмы. Задумывался кто-нибудь над вопросом, сколько звезд на небе? Одним из первых, кто попытался точно ответить на этот вопрос, был древнегреческий астроном Гиппарх. При его жизни в созвездии Скорпиона вспыхнула новая звезда. Гиппарх был потрясен: звезды смертны. Гиппарх составил свой звездный каталог. Он насчитал около тысячи звезд и разбил их по видимому блеску на шесть групп. Самые яркие Гиппрах назвал звездами первой величины, заметно менее яркие – второй, ещё столь же (величина постоянная) менее яркие – третьей и т.д. до звезд, едва видимых невооруженным глазом, которым была присвоена шестая величина.

В наше время существуют чувствительные приборы для световых измерении, – это дает возможность точно определить блеск звезд. Покажем на графике.

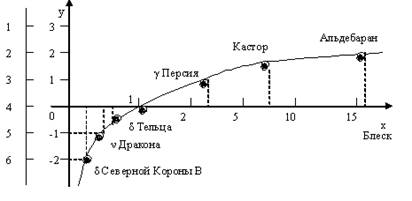
насколько соответствует данным этих измерение распределение звезд по видимому блеску, произведенному на глаз. От каждой из шести групп, на которые распределял звезды Гиппарх, возьмем по одному типичному представителю. По вертикальной оси будем откладывать блеск звезд в единицах Гиппарха, по горизонтальной – показания приборов. Сразу же бросается в глаза, что объективные (прибор) и субъективные (глаз) характеристики блеска не пропорциональны друг другу. С каждым шагом по шкале звездных величин прибор регистрирует возрастание блеска не на одну и ту же величину, а примерно в 2,5 раза. Итак, зависимость выражается логарифмической функцией.

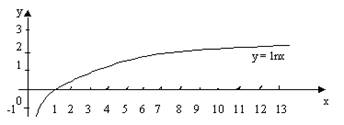
Психофизическими опытами установлено, что величина ощущений изменяется медленнее, чем сила раздражителя. Интенсивность ощущений Е выражается логарифмической зависимостью (закон Вебера – Фехнера) Е = К• lgJ +С, где J – интенсивность раздражителя; K и С – некоторые константы, определяемые данной сенсорной системой.

 

7.Тригонометрическая функция

Еще в четвертом веке у индийцев, в астрономических трудах, встречалось синуса понятье пока в одной четверти. Они назвали “дживой” хорду, что означает “тетива”, и эту хорду за синус принимали . Потом арабы слово исказили, назвали хорду они словом “джайб”. Затем названье на латинском дали и это был двенадцатый уж век, тогда–то джайб и “синусом” назвали. Символику  предложил английский математик в семнадцатом столетье –Норвурд. Эйлер ввел символику, какая есть сейчас. Французский математик Жиль Пирсон впервые синусоиду построил. Затем явился сам Декарт, а с ним и “Геометрия” – его известный всем трактат – и взлет тригонометрии!

“Синусоидой” она называется. Значения функции не всякие бывают, И “ограниченным”  синус называют. (| sinx | < 1) Есть максимальное значенье – единица. И много раз к ней “синус икс” стремится.

Различные колебания окружают нас на каждом шагу. Механические колебания применяются для скорейшей укладки бетона специальными и виброукладчиками , для просеивания материалов на виброситах и даже для почти безболезненного высверливания отверстий в зубах. Акустические колебания нужны для приема и воспроизведения звука, а электромагнитные – для радио, телевидения, связи с космическими ракетами. Электромагнитные колебания доносят до нас вести о сложных процессах, происходящих внутри звезд, о взрывах в отдаленных галактиках, о таких диковинных вещах, как пульсары (нейтронные звезды), черные дыры и т. д. С помощью электромагнитных колебаний учеными были получены снимки обратной стороны Луны и вечно закрытой облаками Венеры.

Колебания сопровождают и биологические процессы, например, слух, зрение, восприятие ультрафиолета, (используемые многими биологическими видами), передачу возбуждения по нервной ткани, работу сердца и мозга. Записывая работу сердца или мозга, врачи получают электрокардиограммы и энцефалограммы. Как говорил создатель учения о биосфере академик Вернадский: “Кругом нас, в нас самих, всюду и везде, без перерыва, вечно сменяясь, совпадая и сталкиваясь, идут излучения разной длины – от волн, длина которых измеряется десятимиллионными долями миллиметра, до длинных, измеряемых километрами”.

Но колебания не всегда полезны. Вибрация станка действует на резец и обрабатываемую деталь и может привести к браку; вибрация жидкости в топливных баках ракеты угрожает их целостности, а вибрация самолетных крыльев при неблагоприятных условиях может привести к катастрофе. Даже хорошо затянутая гайка под влиянием вибрации ослабевает и станок разбалтывается. А самое страшное – под действием вибрации меняется внутренняя структура металлов, что приводит к так называемой “усталости” и последующему неожиданному разрушению конструкции. Колебаниями объясняются случай падения моста, по которому шло в ногу воинское подразделение, а также разрушение мостов во время ураганов, катастрофы в кузнечных цехах, где несколько механических молотов начинали работать в такт. Таким образом, отметим, что колебания, контролируемые человеком, весьма полезны. Однако они могут превратиться в опасного врага. Поэтому надо уметь изучать колебания, знать их свойства. А здесь без математических расчетов не обойтись.

Почему летом теплее, чем зимой? Иногда в ответ на этот вопрос слышишь: потому что Земля, двигаясь по своей орбите, зимой находится от Солнца дальше, чем летом. Но это совершенно неверно! Ведь орбита Земли – это почти круг, в центре которого находится Солнце. Расстояние нашей планеты от светила меняется слишком незначительно от месяца к месяцу, чтобы это было причиной смены времен года. Все дело в наклоне земной оси по отношению к плоскости земной орбиты.

 

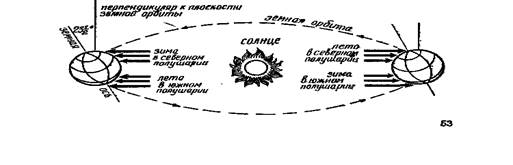
Взгляните на рисунок: зимой в умеренных широтах солнце невысоко поднимается над горизонтом, его лучи лишь скользят по земле. Летом в моменты наивысшего подъема над горизонтом солнце приближается к зениту, его лучи падают почти отвесно на те же участки земного шара. Поток энергии, идущей от Солнца, одинаков во все времена года. Но в зависимости от наклона солнечных лучей она по-разному распределяется по земной поверхности. Больше всего ее приходится на заданный участок поверхности при отвесном падении света. Чем меньше угол, который образуют лучи с поверхностью, тем меньше их приходится на тот же участок. Именно эту зависимость применяет (быть может, не думая об этом) курортник, загорающий под солнцем юга, когда он поворачивает свой топчан так, чтобы солнечные лучи как можно менее отклонялись от перпендикуляра к плоскости топчана.

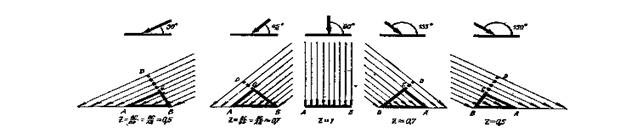
Определим: какая доля солнечной энергии, приходящейся на некоторый участок плоскости при отвесном падении лучей, приходится на него при наклонном падении лучей под тем или иным углом? Проследив эволюцию жирно очерченного прямоугольного треугольника на приведенных чертежах гипотенуза, на которую падают солнечные лучи,– всюду одна и та же. Катет, через который входят падающие на нее лучи,– меняется по длине, уменьшаясь вместе с углом, который образуют с гипотенузой падающие на нее лучи. Очевидно, интересующая нас доля солнечной энергии равна отношению указанного катета к гипотенузе. В прямоугольном треугольнике с заданным углом нужно взять отношение противолежащего катета к гипотенузе. Полученное число и укажет интересующую нас долю солнечной энергии. Число , определенное таким образом и поставленное в соответствие углу, для которого оно определялось, называется синусом этого угла. Это есть синусоида. Если что-то и кажется здесь непривычным, так это неестественно малая протяженность кривой. Обычно ее рисуют безгранично разбегающейся вдоль оси абсцисс, волна за волной.

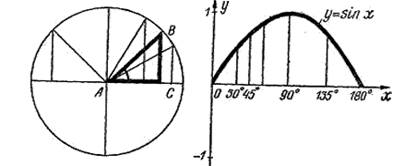
Имени треугольника – “тригонон” – произошло собирательное название “тригонометрические функции”. К ним, кроме синуса, косинуса и тангенса, относятся еще косеканс, секанс и котангенс, соответственно получаемые из перечисленных по правилу обратной пропорциональности

.

 

8.Функции и их графики в нашей жизни

Из всего выше сказанного можно сделать вывод. Изучение функциональных зависимостей необходимо человеку любой профессии.

Используя показания сейсмографов (приборов, непрерывно фиксирующих колебания почвы и строящих специальные графики – сейсмограммы), геологи могут предсказать приближение землетрясение или цунами.

Врачи выявляют болезни сердца с помощью кардиографа, их называют кардиограммами.

 

 

 

 

ЗАКЛЮЧЕНИЕ

 

Изучая и анализируя области применения и взаимосвязь математических функций не только с естественными, но и гуманитарными науками, мы решили поставленные ранее задачи, а значит, добились цели нашего проекта.

Я убедилась в том, что функция является неотъемлемой частью нашей жизни и наук в целом, так как функциональные зависимости, действительно, существуют во всех сферах жизни человека.

Графики и функции широко распространены в нашей жизни, так как они содержательные, наглядные и удобны для передачи и восприятия информации, дальнейшей обработки информации(например, прогнозирование, анализ).

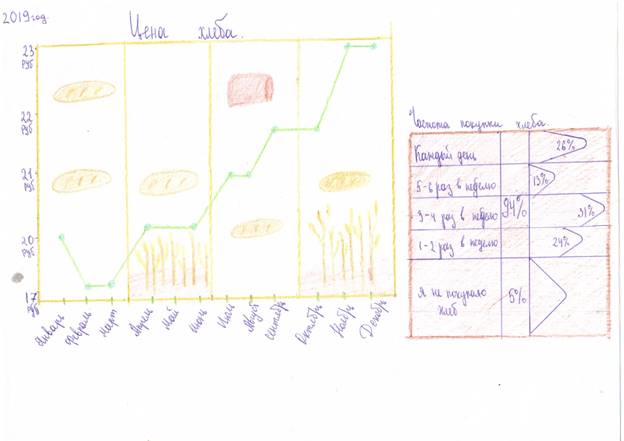
Ученица 10 класса Зияева Аиша составила график зависимости повышения цены хлеба в течение года.

В.В.Путин отметил важность развития массового спорта. Одна из инициатив в этой сфере — возрождение ГТО, благодаря которому выросло не одно поколение активных здоровых людей»,

По мнению главы государства, возрождение системы ГТО в новом формате может принести «огромную пользу» подрастающему поколению.

Одним из видов  обязательных испытаний для школьников 7-16 лет при сдаче норм ГТО является наклон вперед из положения стоя на гимнастической скамье (от уровня скамьи - см) или как его проще называют - тест на гибкость.

Гибкость исключительно важна для сохранения правильной красивой осанки, плавности и лёгкости походки, грациозности движений. Красота и гибкость – почти синонимы.

Гибкость значительно увеличивает диапазон движений, позволяет мышцам работать рационально, затрачивая значительно меньше усилий и энергии для преодоления сопротивления собственного тела как при выполнении самых простых бытовых движений. Так и при движениях требующих отточенного двигательного мастерства.

Достаточная гибкость и эластичность суставов, мышц и связок уменьшают вероятность травм при вынужденных резких движениях, например, при попытки удержать равновесие на льду, выпрямление из глубокого наклона, при неожиданном падении и т.п.

Контрольным упражнением для определения гибкости является наклон вперед из положения стоя

Мы с учителем физкультуры провели измерения на гибкость, выполнив измерения, и составили таблицу

 

 

ПРИЛОЖЕНИЕ

 

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ ГИБКОСТИ СРЕДИ ОБУЧАЮЩИХСЯ ПОЗДНЕЕВСКОЙ СОШ

 

Возраст (лет)	Мальчики			Девочки
	Коли-чество	Средние показатели гибкости	Норма на золотой значок ГТО	Коли-чество	Средние показатели гибкости	Норма на золотой значок ГТО
7	5	5	7	9	6	9
8	9	3	7	8	4	9
9	7	7	8	7	9	11
10	9	5	8	5	6	11
11	5	6	9	10	11	13
12	9	2	9	7	9	13
13	9	3	11	5	7	15
14	8	9	11	4	7	15
15	13	9	11	11	10	15
16	6	6	13	4	5	16

 

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1.                 Виленкин Н. Я. Функции в природе и технике: Книга для внеклассного чтения 9 – 10 кл. – 2 – е изд., испр. – М.: Просвещение, 1993.

2.                 Волович М.Б.  «Справочник школьника 5-11 класс»

3.                 Глейзер Г.И. История математики в школе: 7-8 класс - М.: Просвещение. - 1982.

4.                 Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений / Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. – 9-е изд. – М.: Просвещение, 2001. – 384 с.

5.                 Глейзер Г.И. История математики в школе: 9-10 класс - М.: Просвещение. - 1983.

6.                 Макарычев  Ю.Н. “Алгебра  7 класс”. – 6-е изд. – М. : Издательство “Просвещение”, 1998.

7.                 Ульяновская Н. Н. О, функция, как ты Важна // Математика. – 1999. - №45.

8.                 Виленкин Н.Я. Функции в природе и технике: Кн. для внеклас. Чтения 9-10 кл. – 2-е изд., испр. – М.: Просвещение, 1985. – 192с.

9.                 Интернет-ресурс: http://linear function.ru

10.            Интернет-ресурс: http://ru.wikipedia.org/wiki/ЭТ

 

 

 

Скачано с www.znanio.ru