Исследовательская работа "Математическая статистика в жизни человека"

Муниципальное образовательное учреждение

средняя общеобразовательная школа №93

Советского района г. Волгоград

Математическая статистика в жизни человека

2025

Содержание

Введение..............................................................................................................................................3

Глава 1. Теоретическая часть............................................................................................................4

1.1.Основная информация о математической статистике..............................................................4

1.2.Изучение методов математической статистики........................................................................5

1.3.Основные статистические характеристики, применяемые при исследованиях различных процессов............................................................................................................................................6

1.4.Использование математической статистики в повседневной жизни людей…………………………………………………………………………………...…………..11

Глава 2. Практическая часть...........................................................................................................12

Задача................................................................................................................................................12

Заключение.......................................................................................................................................17

Литература........................................................................................................................................18

Введение

Актуальность: в связи с тем, что метод математической статистики является одним из простейших и нагляднейших, а также широко используется в различных сферах деятельности людей, я решила, что нужно подробнее его изучить.

Цель работы: исследовать применение математической статистики в социальной сфере.

Задачи работы:

1. Необходимо изучить основные понятия, теоремы и алгоритмы математической статистики.

2. Необходимо изучить различные характеристики статистического исследования.

3.   Обобщить и систематизировать знания по данной теме.

4. Применение статистического метода в исследовании процессов, относящихся к социальной сфере деятельности человека.

5.   Предоставить выводы исходя из результатов работы.

Теоретическая часть

1.1.            Основная информация о математической статистике

Математическая статистика — раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы. Большая часть математической статистики основана на вероятностных моделях.

Основными задачами математической статистики являются оценивание и проверка гипотез. Рассматриваются и более частные задачи, связанные с проведением выборочных исследований, восстановлением зависимостей, построением и использованием классификаций и др.

Методы математической статистики являются основной построения большинства аналитических моделей   Data Mining  в задачах классификации, кластеризации, регрессии и распознавания образов.

1.2.            Изучение методов математической статистики

Методы оценки и проверки гипотез основываются на вероятностных и гиперслучайных моделях происхождения данных. Математическая статистика оценивает параметры и функции от них, которые представляют важные характеристики распределений (медиану, математическое ожидание, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используются точечные и интервальные оценки. Современная математическая статистика содержит большой раздел – статистический последовательный анализ, в котором допускается формирование массива наблюдений по одному массиву. Математическая статистика также содержит общую теорию проверки гипотез и большое количество методов для проверки конкретных гипотез (например, о симметрии распределения, о значениях параметров и характеристик, о согласии эмпирической функции распределения с заданной функцией распределения, гипотеза проверки однородности (совпадение характеристик или функций распределения в двух выборках) и др.). Проведением выборочных обследований, связанных с построением адекватных методов оценки и проверки гипотез, со свойствами разных схем организации выборок, занимается раздел математической статистики, имеющий большое значение.

1.3.            Основные статистические характеристики, применяемые при исследованиях различных процессов

Одна из основных задач статистики состоит в надлежащей обработке информации. Конечно, у статистики есть много других задач: получение и хранение информации, выработка различных прогнозов, оценка их достоверности и т. д. Ни одна из этих целей не достижима без обработки данных. Поэтому то, чем стоит заняться — это статистическими методами обработки информации. Для этого нам будут нужны новые термины, принятые в статистике.

Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно, по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на их количество.

Среднее арифметическое является важной характеристикой ряда чисел, но иногда полезно рассматривать и другие средние.

Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчете. Рассмотрим эти свойства.

1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты.

2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю.

3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С.

4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А,  то средняя арифметическая соответственно уменьшится или увеличится на ту же величину.

5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз.

Размах вариации – разница между максимумом и минимумом.

Размах вариации отражает диапазон возможных значений.

Размах является важной характеристикой вариации, он дает первое общее представление о различии единиц внутри совокупности. Этот показатель выражается в тех именованных числах, в каких выражены значения признака.

Особенность размаха вариации заключается в том, что он зависит лишь от двух крайних значений признака. По этой причине его целесообразно применять в тех случаях, когда особое значение имеет либо минимальный, либо максимальный вариант, т.е. когда размах вариации имеет большое смысловое значение. Например, им определяются пределы, в которых могут колебаться размеры тех или иных параметров деталей; его используют при оценке различного рода рисков. Другая сторона этой особенности заключается в том, что на величину размаха вариации большое влияние оказывает случайность. Так как из статистического ряда берутся только два значения признака, причем крайние в ряду, на размах этих значений могут оказывать влияние причины случайного характера, то и размах вариации может быть зависимым от причин случайного характера.

С отмеченной особенностью связано и то обстоятельство, что показатель размаха вариации не учитывает частот в вариационном ряду распределения.

Среднее линейное отклонение – отражает среднее из абсолютных (по модулю) отклонений всех значений анализируемой совокупности от их средней величины.

Показатель размаха вариации дает обобщающую характеристику только размаху (амплитуде) значений признака, но не вариации отклонений. Распределение отклонений можно уловить, исчислив отклонения всех вариантов от средней. Для того чтобы дать им обобщающую характеристику, необходимо вычислить среднюю из этих отклонений, т.е. разностей между значениями признака и средней арифметической в данной совокупности единиц.

Известно, что сумма отклонений значений признака от среднего арифметического всегда равна нулю, так как сумма положительных отклонений всегда равна сумме отрицательных отклонений. Следовательно, чтобы вычислить среднюю арифметическую из отклонений, нужно условно допустить, что все отклонения, положительные и отрицательные, имеют одинаковый знак. Тогда, если взять сумму всех отклонений, условно принятых с одинаковым знаком, и разделить на их число, то полученный показатель вариации будет называться средним линейным отклонением , т.е. это средняя арифметическая из абсолютных значений отклонений отдельных вариантов от их средней арифметической.

Среднее линейное отклонение обладает большим преимуществом перед размахом вариации в отношении полноты характеристики колебания признака. Однако при этом нарушается элементарное правило математики, так как отклонение от среднего значения признака складывается без учета знаков. Это обстоятельство вынуждает искать такой показатель вариации, который был бы лишен и этого недостатка. Хотя в некоторых случаях, суммирование показателей без учета знаков имеет экономический смысл. Например, в практической статистике оборот внешней торговли страны определяется как сумма экспорта и импорта, общий оборот рабочей силы — как сумма принятых и уволенных.

Отмеченный выше недостаток среднего линейного отклонения может быть устранен путем возведения в квадрат отклонений вариантов от средней величины.

Среднее квадратичное отклонение – корень из дисперсии (среднего квадрата отклонений).

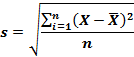
Среднее квадратичное отклонение так же, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения, оно всегда больше среднего линейного отклонения. Среднее квадратичное отклонение измеряет абсолютный размер колебания признака и выражается в тех же единицах измерения, что и значения признака (рублях, тоннах, годах и т.д.). Оно является абсолютной мерой вариации.

Дисперсия – средний квадрат отклонений.

Дисперсия в статистике определяется как среднее квадратичное отклонение индивидуальных значений признака в квадрате от средней арифметической. Распространенный способ расчета квадратов отклонений вариантов от средней с их последующим усреднением.

В экономически-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадратичного отклонения, оно представляет собой корень квадратный из дисперсии.

Характеризует абсолютное колебание значений варьирующего признака выражается в тех же единицах измерения, что и варианты. В статистике часто возникает необходимость сравнения вариации различных признаков. Для таких сравнений используется относительный показатель вариации, коэффициент вариации, который мы рассмотрим позднее.

Свойства дисперсии:

1.Если из всех вариант вычесть какое-либо число, то дисперсия от этого не изменится.

2. Если все значения вариант разделить на какое-либо число b, то дисперсия уменьшится в b^2 раз.

3. Если исчислить средний квадрат отклонений от какого-либо числа с неравного средней арифметической, то он будет больше дисперсии.

Также дисперсию можно определить, как разницу между средним квадратом и средней в квадрате.

Коэффициент вариации наиболее универсальный показатель, отражающий степень разбросанности значений независимо от их масштаба и единиц измерения.

По своему абсолютному значению среднее квадратичное отклонение зависит не только от степени вариации признака, но и от абсолютных уровней вариантов и средней. Поэтому сравнивать средние квадратичные отклонения вариационных рядов с различными средними уровнями непосредственно нельзя. Чтобы иметь возможность для такого сравнения, нужно найти удельный вес среднего отклонения (линейного или квадратичного) в среднем арифметическом показателе, выраженном в процентах, т.е. рассчитать относительные показатели вариации.

Коэффициент вариации измеряется в процентах и может быть использован для сравнения вариации различных процессов и явлений. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. Это считается аксиомой статистики.

1.4.            Использование математической статистики в повседневной жизни людей

Математическая статистика является неотъемлемой частью жизни любого человека из-за того, что в нашу жизнь властно вошли выборы и референдумы, банковские кредиты и страховые полисы, таблицы занятости и диаграммы социологических опросов, нужны и для продолжения образования в таких областях, как социология, экономика, право, медицина, демография и других.

Таблицы и диаграммы широко используются в справочной литературе, в средствах массовой информации. Государственные и коммерческие структуры регулярно собирают обширные сведения об обществе и окружающей среде. Эти данные публикуют в виде графиков, таблиц и диаграмм.

Практическая часть

Задача

Рассмотрим таблицу, содержащую демографические характеристики Волгоградской области за 2018-2023 годы согласно данным Росстата.

Для наглядности, по данным таблицы составим столбчатые диаграммы.

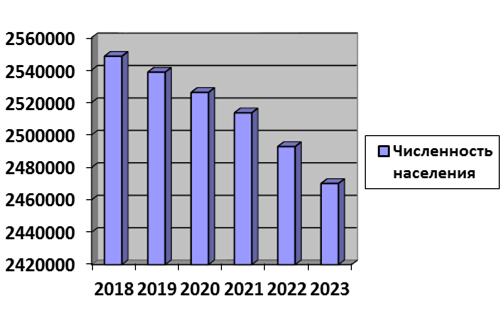Рисунок 1.

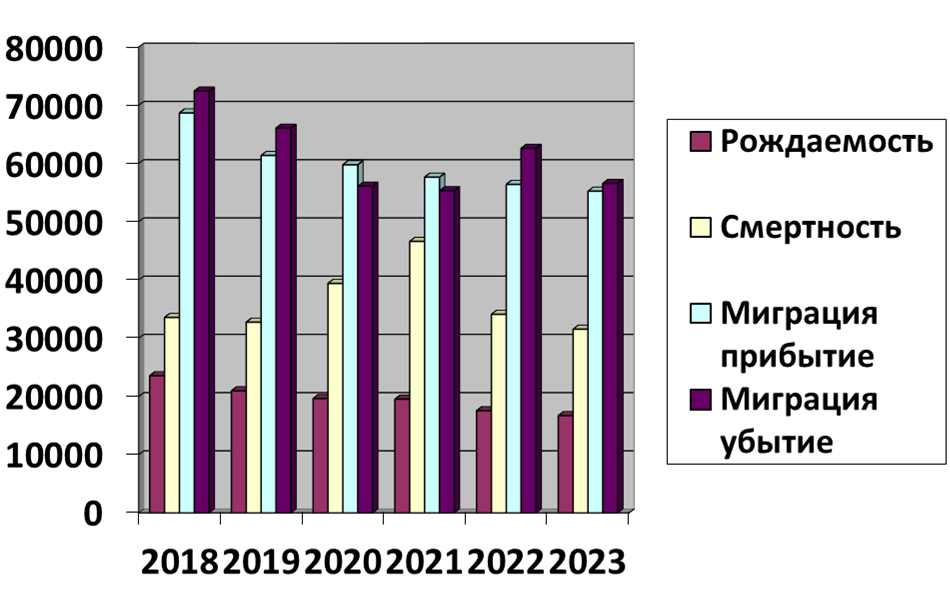Рисунок 2.

Далее, используя статистические характеристики, мы можем узнать, являются ли все данные таблицы однородными, или же какая-то характеристика населения резко изменялась с течением времени.

1.      Численность всего населения Волгоградской области с 2018 по 2023 годы

Рассчитаем среднее арифметическое численности всего населения Волгоградской области с 2018 по 2023 годы:

По формуле найдем среднее квадратичное отклонение численности всего населения Волгоградской области с 2018 по 2023 годы:

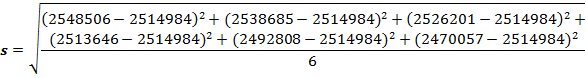
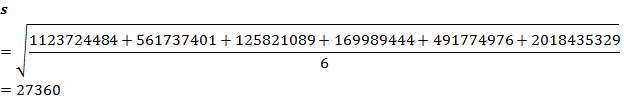
Найдем коэффициент вариации численности всего населения с 2018 по 2023 годы:

Итого: данные таблицы о численности всего населения Волгоградской области с 2018 по 2023 годы однородны, так как коэффициент вариации не превышает 33%.

2.      Рождаемость в Волгоградской области с 2018 по 2023 годы

Рассчитаем среднее арифметическое рождаемости в Волгоградской области с 2018 по 2023 годы:

По формуле найдем среднее квадратичное отклонение рождаемости в Волгоградской области с 2018 по 2023 годы:

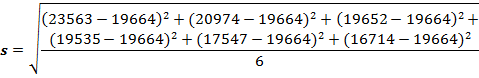
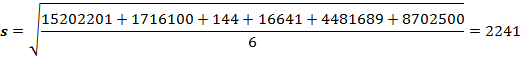
         Найдем коэффициент вариации рождаемости в Волгоградской области с 2018 по 2023 годы:

Итого: данные таблицы о рождаемости в Волгоградской области с 2018 по 2023 годы однородны, так как коэффициент вариации не превышает 33%.

3.      Смертность в Волгоградской области с 2018 по 2023 годы

Рассчитаем среднее арифметическое смертности в Волгоградской области с 2018 по 2023 годы:

По формуле найдем среднее квадратичное отклонение смертности в Волгоградской области с 2018 по 2023 годы:

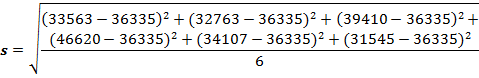
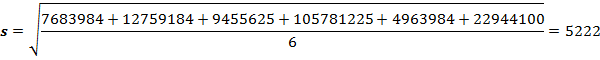
Найдем коэффициент вариации смертности в Волгоградской области с 2018 по 2023 годы:

Итого: данные таблицы смертности в Волгоградской области с 2018 по 2023 годы однородны, так как коэффициент вариации не превышает 33%.

4.      Миграция прибыло в Волгоградской области с 2018 по 2023 годы

Рассчитаем среднее арифметическое миграции прибыло в Волгоградской области с 2018 по 2023 годы:

По формуле найдем среднее квадратичное отклонение миграции прибыло в Волгоградской области с 2018 по 2023 годы:

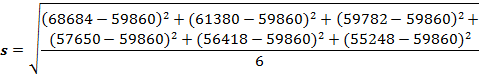
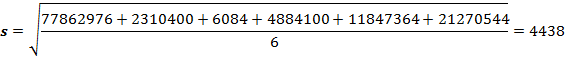
Найдем коэффициент вариации миграции прибыло в Волгоградской области с 2018 по 2023 годы:

Итого: данные таблицы о численности всего населения Волгоградской области с 2018 по 2023 годы однородны, так как коэффициент вариации не превышает 33%.

5.      Миграция убыло в Волгоградской области с 2018 по 2023 годы

Рассчитаем среднее арифметическое миграции убыло в Волгоградской области с 2018 по 2023 годы:

По формуле найдем среднее квадратичное отклонение миграции убыло в Волгоградской области с 2018 по 2023 годы:

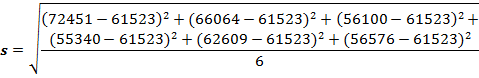
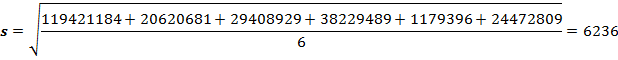
Найдем коэффициент вариации миграции убыло в Волгоградской области с 2018 по 2023 годы:

Итого: данные таблицы о миграции убыло в Волгоградской области с 2018 по 2023 годы однородны, так как коэффициент вариации не превышает 33%.

Заключение

В процессе работы математическая статистика и ее составляющие исследовались нами как самый наглядный инструмент анализа.

Данные, взятые из маркетингового паспорта Волгоградской области за 2018 год, для наглядности были представлены в виде столбчатых диаграмм, а после проанализированы с помощью изученных нами ранее статистических характеристик. Таким образом из рядов чисел мы смогли вычленить интересующую нас информацию.

К сожалению, столбчатая диаграмма на рисунке 1 наглядно показывает нам снижение численности населения в Волгоградской области в период 2019-2023 годов, особенно за последние два года. Однако, с точки зрения статистических характеристик, эти данные по численности населения считаются однородными, так как коэффициент вариации не превышает 33%.  

Столбчатая диаграмма на рисунке 2 показывает нам соотношение рождаемости, смертности, а также миграции населения Волгоградской области в период 2019-2023 годов. К глубокому сожалению, мы видим, что смертность превышает рождаемость, а последние два года миграция выбытие превысила миграцию прибытие. Однако, опять же, с точки зрения статистических характеристик, и эти данные считаются однородными, так как и здесь коэффициенты вариации не превышают 33%. 

Мы наглядно убедились, что с помощью статистических характеристик можно вычленить из общей картины нужную информацию, что подтверждает универсальность математической статистики.

Литература

1.   Данные Росстата по Волгоградской области за 2019-2023 годы

2.   http://mathprofi.ru/matematicheskaya_statistika.html

3.   https://www.booksite.ru/fulltext/1/001/008/074/314.htm

4.   Калинина В.Н. Теория вероятностей и математическая статистика

5.  Хуснутдинов Р.Ш. Сборник задач по теории вероятностей и математической статистике

6.   Шведов А.С. Теория вероятностей и математическая статистика

Скачано с www.znanio.ru