Исследовательская работа "Теорема Вариньона"

ХХV РАЙОННЫЙ КОНКУРС ТВОРЧЕСКИХ ИССЛЕДОВАТЕЛЬСКИХ РАБОТ ШКОЛЬНИКОВ     СЕКЦИЯ МАТЕМАТИКИ       «ТЕОРЕМА ВАРИНЬОНА»                                                    2022 год

 

СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………………….…3

I.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1  Пьер Вариньон и его теорема………………………………………….…….5

1.2  Следствия из теоремы Вариньона…….…………………………… …...…..6

1.3  Теорема Эйлера и теорема о бабочках ……………………………………..8

II. ПРАКТИЧЕСКАЯ ЧАСТЬ

2.1  Задачи из школьного курса геометрии…………….………………..………9

2.2  Конкурсные задачи…………..………..……………...…………………..…..9

2.3 Разбор задач с использованием теоремы Вариньона  и без её использования………………………………………………………………....…12

2.4  Социологические исследования……………………………………...…….14

ЗАКЛЮЧЕНИЕ…………………………………………………………….…..15

СПИСОК ЛИТЕРАТУРЫ…………………………………………………….16

ПРИЛОЖЕНИЯ……………………………………………………………...…17

 

 

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

В 21 век, в век информационных технологий, главным ресурсом является время. Большую часть времени у нас занимает обучение в школе и приготовление домашнего задания. Одним из самых сложных предметов в школе является геометрия. В частности, задачи на доказательство требуют значительной траты времени, поэтому у многих отсутствует интерес к решению подобных заданий.

В теме «Четырехугольники» эту проблему может решить использование теоремы Вариньона. Почти каждая геометрическая задача нестандартна. Параллелограмм Вариньона — надёжный помощник в решении геометрических задач различной сложности. Пьер Вариньон – французский математик и механик 18 века, который первым доказал, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма. Более подробному изучению этой теоремы, которая будет экономить моё время и время  моих друзей, я и решила посвятить свою исследовательскую работу. Я захотела убедиться в том, что теорема Вариньона и ее следствия — надёжные помощники в решении геометрических задач различной сложности.

Гипотеза: теорема Вариньона и следствия из нее помогают решать геометрические задачи быстрым способом.

Объект исследования:  теорема Вариньона и следствия из нее.

Предмет исследования:  планиметрические задачи с использованием теоремы Вариньона для решения.

Цель исследования: проверить помогают ли знания о теореме Вариньона и ее следствий решать задачи с наименьшими временными затратами.

Задачи исследования: 

1.     Изучить теоретический материал: параллелограмм Вариньона,

бимедианы четырехугольника, теорема Вариньона и следствия из нее.

2.     Рассмотреть различные приемы решения планиметрических задач

3.     Сравнить решения одной и той же задачи, применяя теорему Вариньона и традиционный подход.

4.     Выяснить практическое применение данной теоремы в задачах по геометрии школьного курса и в конкурсных задачах. 

5.     Сравнить количество времени, необходимое для решения задач традиционным способом и используя теорему Вариньона.

6.     Показать решение олимпиадных заданий с помощью параллелограмма Вариньона.

Методы исследования: изучение литературы, сбор информации о параллелограмме Вариньона, выполнение чертежей к задачам, осмысление собранной информации.

Практическая значимость исследования: подбор и обобщение информации о параллелограмме Вариньона могут быть представлены школьникам и учителям для проведения практических занятий на элективных курсах с учащимися выпускных классов и при подготовке к Единому Государственному Экзамену и поступлению в ВУЗ. Также изучение данной темы поможет более глубоко подготовиться к вступительным экзаменам и успешному участию в математических конкурсах и олимпиадах.
Актуальность темы:

1. Применение опыта решения планиметрических задач с использованием теоремы Вариньона и следствий из нее помогает повысить уровень логической культуры.

2. Изучение данной темы поможет подготовиться к  успешному участию в математических конкурсах и олимпиадах.

3. Данная работа может быть использована для проведения практических занятий на элективных курсах с учащимися выпускных классов и при подготовке к Единому Государственному Экзамену и поступлению в ВУЗ.

 

 

 

 

I.ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

 

1.1  Пьер Вариньон и его теорема

Пьер Вариньон, французский механик и инженер, член Парижской Академии наук, профессор математики коллежа Мазарини, родился во Франции в 1654 году. Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году. Вариньон готовился к религиозной деятельности, но, изучая сочинения Эвклида и  Декарта, увлекся математикой и механикой. Труды Вариньона посвящены теоретической механике, анализу бесконечно малых, геометрии, гидромеханике и физике. Вариньон был другом Ньютона, Лейбница  и Бернулли (Приложение 1).

Вариньон написал учебник по элементарной геометрии, изданный в 1731 году, в котором впервые использовалось определение бимедиан четырехугольника. Бимедианы четырехугольника – это отрезки, соединяющие середины противоположных сторон. А параллелограмм KLMN называется параллелограммом Вариньона данного четырехугольника  ABCD. (Приложение 2). В вышесказанном учебнике также приводилось доказательство теоремы Вариньона.

Теорема:  Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника (Приложение 3)

Дано:  ABCD – выпуклый четырехугольник; AK=KB; BL=LC; CM=MD; AN=ND  

Доказать: 1) KLMN – параллелограмм;  2) S_KLMN= S_ABCD/2

Доказательство: 1) Рассмотрим одну из сторон четырехугольника KLMN , например KL . Так как KL является средней линией треугольника ABC , то KL ║AC . По тем причинам MN ║AC . Следовательно, KL ║NM  и KL= MN= AC/2 . Тогда  KLMN  - параллелограмм.  

2) Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника. Поэтому

 

сама сумма площадей первого и третьего треугольников равна четверти площади всего четырехугольника. То же и относительно суммы площадей второго и четвертого треугольников. Поэтому площадь параллелограмма KLMN составляет половину площади четырехугольника  ABCD. Теорема доказана.

1.2  Следствия из теоремы Вариньона

Следствие 1 Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны (Приложение 3)

1)   Дано: ABCD – четырехугольник; KLMN – пар-м Вариньона; AC=BD.

Доказать: KLMN – ромб.

Доказательство:  Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.

2)  Дано: ABCD – четырехугольник; KLMN – пар-м Вариньона; KM  LN

Доказать: KLMN – ромб.

Доказательство:  Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба). Что и требовалось доказать.

Следствие 2  Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике 1) диагонали перпендикулярны 2) бимедианы равны (Приложение 4)

1)  Дано: ABCD – четырехугольник; KLMN – пар-м Вариньона; AC  BD.

Доказать: KLMN – прямоугольник.

Доказательство:  Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно,

 

 

параллелограмм Вариньона является прямоугольником. Что и требовалось доказать.

2)  Дано: ABCD – четырехугольник; KLMN – пар-м Вариньона; KM = LN

Доказать: KLMN – прямоугольник.

Доказательство:  Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).Что и требовалось доказать.

Следствие 3 Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны;  2) бимедианы равны и перпендикулярны (Приложение 4)

1)  Дано: ABCD – четырехугольник; KLMN – пар-м Вариньона; AC  BD; АС=ВD

Доказать: KLMN – квадрат.

Доказательство:  Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом. Что и требовалось доказать.

2)  Дано: ABCD – четырехугольник; KLMN – пар-м Вариньона; KM=LN;KM LN

Доказать: KLMN – квадрат.

Доказательство:  Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата). Что и требовалось доказать.

Следствие 4 Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам. (Приложение 5)

Доказательство: Пусть KM и LN – бимедианы ABCD, PQ – отрезок, соединяющий середины диагоналей АС и BD. То, что бимедианы KM и LN точкой пересечения делятся пополам, следует из того, что эти отрезки являются диагоналями параллелограмма Вариньона. Поэтому

 

нам достаточно доказать, что отрезки PQ и LN их точкой пересечения делятся пополам (обращаем внимание на то, что в невыпуклом четырехугольнике одна из диагоналей расположена вне четырехугольника). Используя теорему о средней линии треугольника для соответствующих треугольников, имеем: LQ║ CD║ PN и PL║ AB║ NQ. Тем самым, PLQN – параллелограмм. По свойству параллелограмма следует, что отрезки PQ и LN их точкой пересечения делятся пополам. Что и требовалось доказать.

 

1.3  Теорема Эйлера и теорема о бабочках

Теорема Эйлера:  Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверённый квадрат отрезка, соединяющего середины диагоналей, то есть   . (Приложение 6)

Доказательство: Уже было отмечено что LPNQ – параллелограмм. Поэтому . В последнем равенстве мы дважды воспользовались теоремой о средней линии треугольника. Аналогично для параллелограмма KPMQ имеем:   .                                                 

Кроме того,   . Так как KLMN – параллелограмм Вариньона четырехугольника ABCD . Складывая первые два равенства и учитывая последнее, получаем соотношение Эйлера.

Теорема о бабочках: Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан  LN и KM выпуклого четырехугольника ABCD равны. (Приложение 7)

Доказательство: Воспользуемся теоремой о средней линии треугольника. Получаем:                                                             

Что и требовалось доказать.

 

 

 

 

 

II. ПРАКТИЧЕСКАЯ ЧАСТЬ

2.1  Задачи из школьного курса геометрии

Рассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые встречаются в школьном курсе геометрии.

Задача 1. Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.

Доказательство:

а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (см. следствие 1);

Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1).

б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2);

Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника (см. следствие 2).

Задача 2. У четырехугольника диагонали равны a и b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Решение:    Периметр параллелограмма Вариньона равен a+ b .

2.2  Конкурсные задачи

Рассмотрим задачи на бимедианы четырехугольника и теорему Вариньона, которые взяты нами с различных математических конкурсов и олимпиад.

Задача 3. Докажите, что площадь параллелограмма, образованного прямыми, проходящими через вершины выпуклого четырехугольника и параллельными его диагоналям, в два раза больше площади исходного четырехугольника. (Приложение 8)

Доказательство: .

 

 Так как AMOL, MONB, CKON, DKOL - параллелограммы, то 

 Отсюда получаем, что

.Что и требовалось доказать.

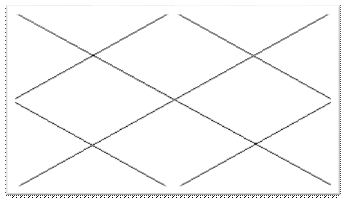
Задача 4. Все стороны выпуклого четырехугольника площади 1 разделены на 2n равных частей, а затем точки деления на противоположных сторонах соединены так, чтобы получилась «косоугольная шахматная доска», состоящая из белых и черных «клеток» (см. рис. при n= 2). Доказать, что сумма площадей всех белых «клеток» равна сумме площадей всех черных «клеток».(Приложение 9)

Доказательство:  Из следствия 2 следует, что точки пересечения отрезков на этой доске делят каждый на равные части. Тогда в любом «маленьком» четырехугольнике, куда входят ровно две белые и две черные клетки, выполняются условия теоремы о бабочках. Нужное равенство установлено.

Задача 5. Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий. (Приложение 10)

Доказательство: Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей. Что и требовалось доказать.

Задача 6. Докажите, что суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан  LN  и  KM  выпуклого четырехугольника ABCD равны. (Приложение 11)

Доказательство:   Воспользуемся теоремой о средней линии треугольника.

Получаем: S_BKL + S_DMN = (S_ABC + S_ADC)/4 = S_ABCD/4 = (S_ABD + S_CBD)/4 = S_AKN+S_CLM

Что и требовалось доказать.

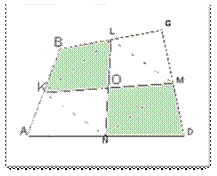
Задача 7.  На продолжениях сторон выпуклого четырехугольника  ABCD  выбраны точки   так, что  и точка  находится между и B, точка B – между  и C, точка C  – между и D, точка D – между  и . Докажите, что  = .
(Приложение 12)

 

Доказательство: 

 ;;
;;;;
Отсюда получаем, что  .
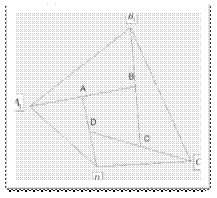
Задача 8.  Пусть L и N – середины противоположных сторон  BC  и  AD  четырехугольника ABCD . Доказать, что площадь четырехугольника  LPNQ  равна сумме площадей треугольников  ABP  и  CQD. (Приложение 13)

Доказательство: Покажем, что . В треугольнике  ACD медиана CN делит его на два треугольника равной площади, а в треугольнике ABC медиана AL делит его на два равновеликих треугольника. Так как , то . Аналогично устанавливается нужное равенство и для четырехугольника  NBLD . Теперь утверждение задачи следует из того, что четырехугольники ALCN и NBLD покрывают внутри четырехугольника ABCD два раза четырехугольник LPNQ и не покрывают треугольники ABP и CQD, а их сумма их площадей равна площади четырехугольника ABCD. Площадь четырехугольника, с другой стороны, равна сумме площадей шести треугольников (в том числе и треугольников ABP и CQD) и интересующего нас четырехугольника LPNQ.
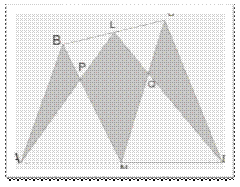
Задача 9.  Пусть K, L, M, N – середины сторон (рис. 13) выпуклого четырехугольника ABCD. Докажите, что площадь четырехугольника, образованного прямыми CK, AM, BN, DL, равна сумме площадей четырех треугольников, отмеченных на рисунке. (Приложение 14)

Доказательство:  Так как , то из этого следует, что четырехугольники AKCM и BLDN покрывают внутри четырехугольника  ABCD два раза четырехугольник, образованный прямыми CK, AM, BN, DL, и не покрывают четыре треугольника, а сумма их площадей равна площади четырехугольника ABCD. Отсюда следует, что площадь четырехугольника,

 

образованного прямыми CK, AM, BN, DL, равна сумме площадей четырех треугольников, отмеченных на рисунке .

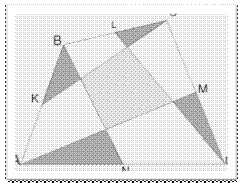
Задача 10.  Противоположные стороны четырехугольника ABCD разделены на три равные части и точки деления попарно соединены. Доказать, что одна из площадей получившихся трех четырехугольников равна.
 (Приложение 15)

Доказательство:  Докажем, что площадь среднего четырехугольника равна трети площади исходного четырехугольника. Другими словами докажем, что
. Чтобы в этом убедиться, достаточно проверить, что
. А последнее равенство есть следствие того, что основания AE, EF, FD всех трех треугольников в этом равенстве равны, а высота треугольника EH F является средней линией трапеции с основаниями, равными высотам треугольников AGE и FCD.

2.3  Разбор задач с использованием теоремы Вариньона  и без её использования

Задача 11.  Докажите, что середины сторон прямоугольника являются вершинами ромба и наоборот. (Приложение 16)

Доказательство:

Способ №1

AC – диагональ. KL - средняя линия треугольника ABC. NM – средняя линия треугольника ADC. Треугольники ABC и ADC равны по третьему признаку равенства треугольников (AB=DC, BC=DC, AC – общая сторона) => KL=NM. Также KL||NM (AC||NM, AC||KL) => KLMN- параллелограмм.
Из первого следует, что KL=NM. Аналогично можно доказать, что LM=KN. 
ABCD – прямоугольник => AC=BD. => KL=LM=MN=NK=> KLMN – ромб. 
Способ №2

Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба. Стороны прямоугольника

 

перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (см. следствие 1).

Задача 12. У четырехугольника диагонали равны a и b. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Решение:
Способ №1

Подобно предыдущей задаче, нужно доказать, что KLMN – параллелограмм.
KL||AC||NM KL=NM=0,5AC, а LM||BD||KN, а LM=KN=0,5BD.  
P(ABCD)=KL+NM+LM+KN = 0,5AC+0,5AC+0,5BD+0,5BD=BD+AC=a+b.
Способ №2

Периметр параллелограмма Вариньона равен a+b.

Задача 13.  Пусть K,L,M,N– середины сторон выпуклого четырехугольника  ABCD. Докажите, что , где – угол между бимедианами четырехугольника;  ,где – угол между диагональю AC и бимедианой LN.(Приложение 17)

Доказательство:
Способ №1

То, что KLMN – параллелограмм мы уже доказали в предыдущих задачах.
Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника. Поэтому сама сумма площадей первого и третьего треугольников равна четверти площади всего четырехугольника. То же и относительно суммы площадей второго и четвертого треугольников. Поэтому площадь параллелограмма KLMN составляет половину площади четырехугольника ABCD.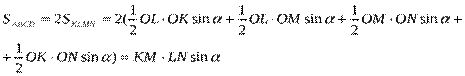

Способ №2

Так как KLMN- параллелограмм Вариньона, а KM и NL – бимедианы, то , где O – точка пересечения бимедиан (см. следствие 2),  (см. теорему Вариньона).

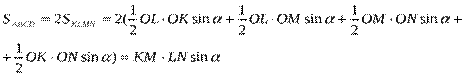
2.4  Социологические исследования

 

Чтобы ответить на вопрос исследования, был проведен классный час по теме «Теорема Вариньона», а  затем предложено учащимся 8 и 9 класса решить задачи двумя способами (с использованием теоремы Вариньона и ее следствий при решении задачи и без нее). В исследовании принимало 8 учащихся. По результатам социологического исследования были выявлены закономерности (Приложение 18).

На диаграмме №1 видно, что затраченное время на решение предложенной задачи находилось в пределах от 18 до 32 минут. В среднем можно сказать, что 26 минут тратить учеником на решение геометрической задачи, не используя знания о теореме Вариньона и ее следствий.

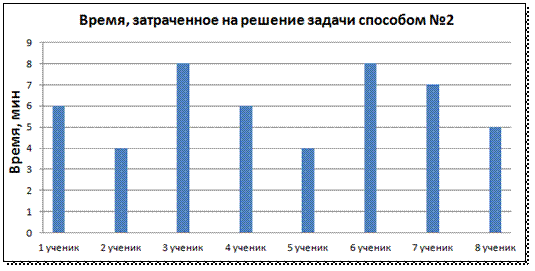
Рассматривая же результаты решения задачи на диаграмме №2 с использованием знаний о теореме Вариньона и ее следствий, видно, что затраченное время находилось в пределах от 4 до 8 минут. В среднем можно сказать, что  6 минут тратить учеником на решение геометрической задачи вторым способом. 

Результаты исследования подтвердили нашу гипотезу о наименьших временных затратах при решении геометрических задач с использованием теоремы Вариньона и следствий из нее.

 

 

 

ЗАКЛЮЧЕНИЕ

«Нет ничего нового под солнцем, но есть кое-что

старое, чего мы не знаем»,

Лоренс Питер

Пьер Вариньон жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.

Поэтому была поставлена цель: проверить помогают ли знания о теореме Вариньона и ее следствий решать задачи с наименьшими временными затратами.

Для этого был разобран весь теоретический материал, решены задачи базового уровня, а также повышенной сложности (олимпиадные). Было подсчитано, что на решение задачи традиционным способом затрачивается 26 минут, а зная теорему Вариньона и следствия из нее, доказательство сводится к одному-двум предложениям и занимает 6 минут. При этом экономия времени на доказательство в среднем составляет 20 минут. Таким образом, уже даже решения трех задач добавят дополнительные сорок пять минут (т.е. целый урок) на доказательство других, более сложных.

От этого повышается не только интерес к изучению данного предмета, но и сам процесс работы приносит удовлетворение. Цель работы считаю достигнутой.

 

 

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

1.     Филипповский Г. Б. Параллелограмм Вариньона решает задачи //Математика в школе № 4 – 2006.

2.     В. Вавилов, П. Красников. Бимедианы четырехугольника//Математика. 2006 – №22.

3.     Геометрия: Учебник для 7 – 9 кл. общеобразовательных учреждений /Л. С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др, – М.: Просвещение.

4.     Геометрия: Доп. главы к шк. учеб. 8 кл.: Учеб. пособие для учащихся школ и классов с углубленным изучением математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение.

5.     Погорелов А. В. Геометрия: Учеб. для 7 – 11 кл. сред. шк.- М.: Просвещение.

6.      ШтейнгаузГ.Математический калейдоскоп. – М.:наука.

7.      Прасолов В.В. задачи по планиметрии. – Т.1, 2. – М.: Наука.

8.     Коксетер Г. С. М., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука.

9.     Интернет-ресурсы ru.wikipedia.org/wiki/Вариньон,_Пьер

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЯ

Приложение 1

Пьер Вариньон  (1654г – 23.12.1722г)

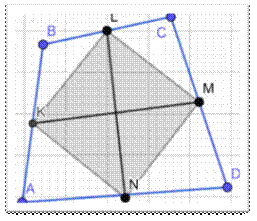
Приложение 2

Бимедианы LN и KM  четырехугольника АВСD

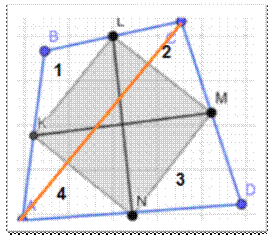
       Приложение 3

Теорема Вариньона

 

 

Приложение 4

Следствия из теоремы Вариньона

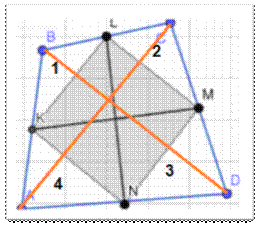
Приложение 5

Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей

     

 

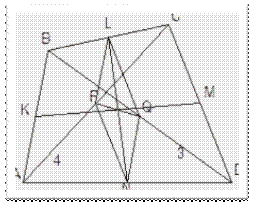
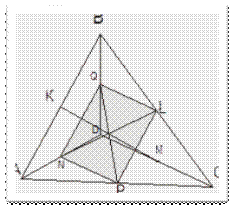
Приложение 6

Теорема Эйлера

 

 

 

 

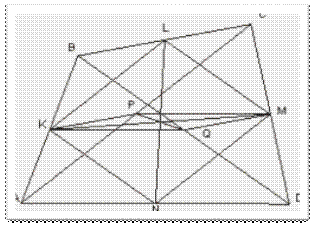
Приложение 7

Теорема о бабочках

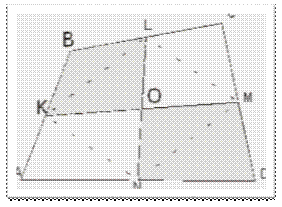
Приложение 8

Конкурсная задача 3

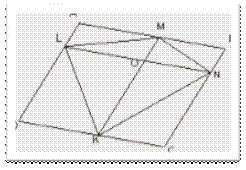
Приложение 9

Конкурсная задача 4

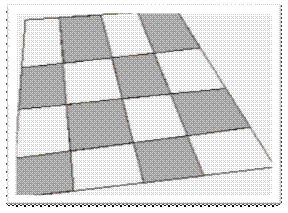
   Приложение 10

Конкурсная задача 5

 

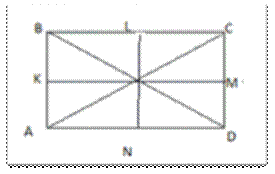
Приложение 11

Конкурсная задача 6

                    Приложение 12

Конкурсная задача 7

Приложение 13

Конкурсная задача 8

Приложение 14

Конкурсная задача 9

 

Приложение 15

Конкурсная задача 10

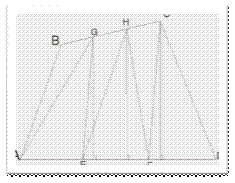
Приложение 16

Разбор задачи 11 с использованием теоремы Вариньона  и без её использования

 

 

 

 

 

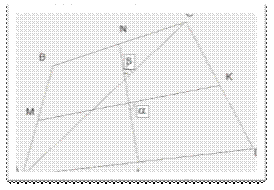
Приложение 17

Разбор задачи 13 с использованием теоремы Вариньона  и без её использования

 

 

 

 

 

 

 

Приложение 18

Результаты проведения исследования

Диаграмма №1

 

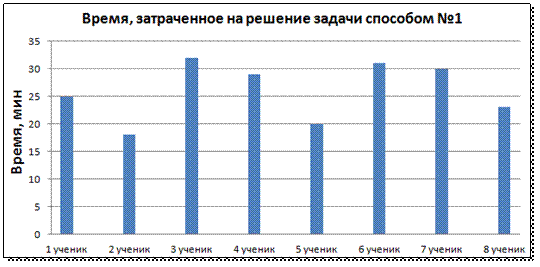
Диаграмма №2

 

Скачано с www.znanio.ru