Исследовательская работа "Теория многочленов"

                   Муниципальное общеобразовательное учреждение

         «Средняя школа №93 Советского района г. Волгограда»

 

 

 

 

 

 

    «Теория многочленов в решении уравнений»

 

 

                                                                                                                                Выполнила:

                                                                                                                                        Слугина Екатерина

                                                                                                      ученица 10 «А» класса МОУ СШ №93

                                                                                                              Советского района г. Волгограда

  

                                                                                                               Руководитель: Березенцева И.И

                                                                                                                                      учитель математики

                                                                                                                                                  МОУ СШ №93

 

 

                                                     2019-2021

 

Оглавление

Введение…………………………………………………………………………………………….

МНОГОЧЛЕНЫ С ОДНОЙ ПЕРЕМЕННОЙ…………………………………………….

§1. Действия с многочленами. Степень многочлена…………………………

§2. Значение и корни многочленов…………………………………………………...

§3. Корни и линейные множители многочленов………………………………

Заключение………………………………………………………………………………………….

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                          Введение

Актуальность темы

Для изучения я выбрала тему «Теория многочленов в решении уравнений», так как она, в отличие от большинства тем школьного курса алгебры, представляет собой математический аппарат для решения задач более широкого содержания, прежде всего решения уравнений и вопросов делимости целых и натуральных чисел.

Цель работы:

Изучить применение теории многочленов в решении уравнений степени >2

Задачи работы:

1.                     Необходимо изучить основные понятия, теоремы и алгоритмы теории многочленов.

2.                     Обобщить и систематизировать знания по данной теме.

3.                     Продемонстрировать применение основных методов решений на наглядных примерах.

4.                     Предоставить выводы по данной теме.

 

 

 

 

 

                         

 

                        Многочлены с одной переменной.

      §1. Действия с многочленами. Степени многочлена.

Многочлен – это алгебраическое выражение, представляющее сумму или разность нескольких одночленов.

Многочленом от одной переменной называется выражение вида

f=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n, где n – любое натуральное число или 0, коэффициенты а₀, а₁, …, а(n-1), а(n) – произвольные числа.

Часто вместо f пишут f(х). Это более сложное обозначение полезно, если необходимо подчеркнуть, что в качестве переменной рассматривается именно х.

Номера коэффициентов называются индексами – начинаются с 0 и идут в возрастающем порядке, так что а₀ – коэффициент при хⁿ, а₁ – коэффициент при x^n-1 и т.д.

Отдельно отмечу случай n=0: при этом многочлен f=a₀, т.е. является числом. Если к тому же а₀=0, то многочлен f имеет специальное название – нулевой многочлен.

Напомню, что степенью многочлена с переменной х называется наибольший из показателей степени одночленов, входящих в его стандартный вид. Поэтому если а₀≠0, то многочлен f=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n имеет степень n.

Степень многочлена f часто обозначается через degf. Например,

deg (2x-1+3x²)=2, deg x⁵=5. Особо отмечу важный «крайний» случай – когда многочлен является числом f=a. Здесь придётся рассмотреть два случая. Если а≠0, то степень f считается равной 0: например deg5=0. Это определение вполне естественно: считая, как обычно, что х⁰=1, мы можем записать f=ax⁰, так что 0 – наибольший из показателей степени одночленов, входящих в запись f.

При а=0 считается, что f степени не имеет: нулевой многочлен не имеет степени.

И ещё два термина. Коэффициент при наибольшем показателе степени х многочлена называется старшим коэффициентом этого многочлена, а слагаемое, не содержащее х, - свободным членом многочлена.

Из правила перемножения двух многочленов немедленно следует, что старший коэффициент произведения двух ненулевых многочленов равен произведению их старших коэффициентов. Из этого факта следует, в частности, два важных теоретических утверждения:

1.         Произведение двух ненулевых многочленов является ненулевым многочленом.

Можно сказать и иначе, если произведение двух многочленов равно нулевому многочлену, то хотя бы один из этих многочленов нулевой.

Символически можно записать так:

     

2.         Степень произведения двух ненулевых многочленов равна сумме степеней этих многочленов.

Формально deg fg=deg f+deg g (f, g ≠0).

Оба этих утверждения, очевидно, остаются верными и для любого числа многочленов.

Отмечу ещё одно свойство многочленов:

3.         Свободный член произведения двух многочленов равен произведению их свободных членов.

Это утверждение также немедленно следует из правила умножения многочленов.

В заключение отмечу, что сложение и умножение многочленов обладают теми же свойствами, что и соответствующие арифметические операции над числами, в множествах целых и рациональных чисел. Именно: для любых многочленов f, g и h справедливы равенства f+g=g+f, fg=gf, (f+g)+h=f+(g+h), (fg)h=f(gh), (f+g)h=fh+gh.

Кроме того, сложение многочленов имеет обратную операцию – вычитание. Она определяется так же, как и во всех числовых множествах. Напомню, что число с называется разностью чисел а и b, если выполняется равенство а=b+с. Разность чисел а и b обозначается через а-b. Другими словами,

с=а-b в том и только в том случае, когда а=b+с.

Символически:

Буквально так же, только в других обозначениях, выглядит определение разности многочленов:

h=f-g в том и только в том случае, когда f=g+h,

Указанные свойства сложения и умножения многочленов и существование разности многочленов позволяют нам употреблять термин из «нешкольной» науки алгебры и называть множество многочленов кольцом.

 

              §2. Значения и корни многочленов.

В многочлен, как и в любое буквенное выражение, можно вместо переменной подставлять числа, и в результате он превращается в числовое выражение, т.е. в конечном счёте в число. Если многочлен обозначен буквой f, а с – некоторое число, то значение f при х=с обозначается через f(с). Число f(с) часто называют также значением многочлена f в точке с.

Например, если f=2x³-5x-6, то f(2)=2*2³-5*2-6=0, f(0)=-6, f(1)=2-5-6=-9, f(-1)=-2+5-6=-3.

В общем виде если, например, f=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n и с – некоторое число, то f(c)=a₀cⁿ+a₁c^n-1+…+a_n-1c+a_n.

Особо отмечу «крайний» случай, когда f – многочлен нулевой степени, т.е. f=а, где а – число, так что f в действительности не содержит переменной. В этом случае считают, естественно, что его значение при любом х равно а.

Поэтому такие многочлены называются постоянными или константами (от латинского constantum – постоянство). Нулевой многочлен также является константой: все его значения равны нулю.

Сделаю два важных для решения задач замечания:

1.                     Значение f (0) равно свободному члену многочлена.

2.                     Значение f (1) равно сумме коэффициентов многочлена.

Действительно, если f=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n, то f(0)=a_n, f(1)=a₀+a₁+…+a_n-1+a_n. Нахождение значений многочлена в соответствии с определением не представляет никаких принципиальных трудностей, однако вычисления при этом могут оказаться достаточно громоздкими. Для упрощения вычислений существует прием, называемый схемой Горнера - по имени английского математика 16 века. Эта схема состоит в заполнении некоторой таблицы из двух строк.

Например, чтобы вычислить значение многочлена f=2x⁴-9x³-32x²-57 при х=7, строка его коэффициентов записывается первой, старший коэффициент «дублируется» во второй строке, а перед ним ставится значение переменной 7, при котором мы вычисляем значение многочлена. Получается таблица, пустые клетки которой и предстоит теперь заполнить:

Это делается по единому правилу: стоящее слева от заполняемой клетки число умножается на 7 и складывается с числом, стоящим над ней. Поэтому в первой пустой клетке ставится число 2*7-9=5, во второй клетке ставится 5*7-32=3, в третьей 3*7+0=21, и в последней – 21*7-57=90

Полностью заполненная схема Горнера выглядит так:

Такие «непонятные» вычисления приводят к ответу: f (7) = 90 – это последнее число второй строки. Желающие могут проверить результат непосредственной подстановкой: f(7)=2*7⁴-9*7³-32*7²-57 и сравнить время, затраченное на вычисления значений многочлена в электронных машинах составляется именно в соответствии со схемой Горнера. На доказательстве правильности вычисления значений многочлена по схеме Горнера я останавливаться не буду.

Одной из основных задач, ради которой в математике и развивалась теория многочленов с одной переменной, является решение так называемых целых алгебраических уравнений произвольных степеней и с произвольными коэффициентами, т.е. уравнений вида a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n.

В связи с решением уравнений вводится важнейшее понятие – корень многочлена.

О п р е д е л е н и е. Число с называется корнем многочлена f, если f (с)=0.

Другими словами, число с является корнем многочлена f, если

a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n

Это равенство означает, что число с является корнем уравнения

a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n

т.е. при подстановке вместо х числа с получается верное неравенство. Поэтому корень многочлена f и корень соответствующего уравнения f(x)=0 – это одно и то же.

Понятно, что схема Горнера позволяет проверять, является данное число с корнем данного многочлена или нет: с её помощью мы как раз и вычисляем значение f(c).

Если требуется проверить несколько значений с, то для экономии выкладок строят не три отдельные схемы, а одну – объединённую. Например, для многочлена f= 3x⁵-5x⁴-7x²+12 и чисел с=1;-1;2 составляется таблица:

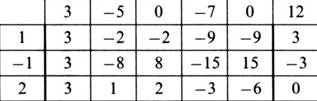
Конечно, при заполнении третьей и четвертой строк таблицы «работает» только первая строка – строка коэффициентов многочлена f. Я вижу, в частности, что из трёх рассмотренных чисел только с=2 является корнем данного уравнения.

 

 

            §3. Корни и линейные множители многочленов.

Из школьной практики я знаю, что для решения уравнений вида f(x)=0 очень полезно разложить f(x) на множители: если f(x)=g(x)*h(x), то дальнейшее сводится к решению двух более простых уравнений g(x)=0 и g(x)=0.

Однако, найдя даже несколько корней уравнения, я далеко не всегда решу уравнение. Например, для уравнения x⁴-x³-6x²-x+3=0 легко подобрать корни – 1,3, но, что делать дальше, неясно.

Между тем небольшое продвижение в теории существенно поможет нам в решении уравнений. Понятие корня тесно связано с разложением многочленов на множители, точнее, с выделением в многочлене линейного множителя. Но если, решая уравнение f(x)=0, я смогу разложить многочлен f на множители, то далее остается решать уравнения меньших степеней.

Основной здесь является следующая теорема, состоящая из двух утверждений и носящая имя французского математика 18 в. Ж. Безу.

Теорема 1 (Безу)

Пусть f – многочлен, с – некоторое число.

1.                     f делится на двучлен х–с тогда и только тогда, когда число с является его корнем.

2.                     Остаток от деления f на х-с равен f(c)

Д о к а з а т е л ь с т в о. Сначала я докажу второе утверждение. Для этого разделю f с остатком на х-с:

F=(x-c)q+r

По определению остатка многочлен r либо равен 0, либо имеет степень, меньшую степени х-с, т.е. меньшую 1. Но степень многочлена меньше 1 только в случае, когда она равна 0, и поэтому в обоих случаях r на самом деле является нулём или отличным от нуля числом.

Подставив теперь в равенство f=(x-c)q+r значение х=с, я получу f(c)=(c-c)q(c)+r, так что действительно r=f(c), и второе утверждение доказано. Теперь первое утверждение почти очевидно. В самом деле, утверждение «f делится на х-с» означает, что остаток от деления равен 0. Но остаток по доказанному равен f(c), так что «f делится на х-с» означает то же самое, что и f(c)=0.

Теорема Безу даёт возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого на 1 меньше: если f(c)=0, то f=(х-с)q и, остаётся решить уравнение q(х)=0. Иногда этим приёмом – он называется понижением степени – можно найти все корни многочлена. В частности, подобрав один корень кубического уравнения, можно его полностью решить – после понижения степени достаточно решить полученное квадратное уравнение.

При решении таких задач большую пользу приносит всё та же схема Горнера. Напомню, что в конце второй строки этой схемы получается значение многочлена f при х=с. Однако на самом деле схема Горнера даёт гораздо больше: числа, стоящие во второй строке (не считая последнего), - это коэффициенты частного от деления на х-с.

Ранее я построила схему Горнера для многочлена

f=3x⁵-5x⁴-7x²+12 и c=1, -1, 2:

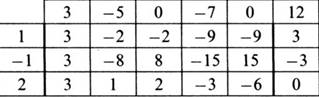
Мы можем убедиться, что, составив по каждой из трёх «вторых» строк соответствующий многочлен степени 4, мы действительно получим частные:

f=(3x⁴-2x³-2x²-9x-9)(x-1)+3, f=(3x⁴-8x³+8x²-15x+15)(x+1)-3,f=(3x⁴+x³+2x²-3x-6)(x-2)

Решу в качестве примера уравнение x⁴-x³-6x²-x+3=0.

Целые корни многочлена f=x⁴-x³-6x²-x+3 должны быть делителями свободного члена, так что это могут быть только числа ±1 и ±3. При этом 1 не является корнем многочлена f, поскольку сумма его коэффициентов, очевидно, не равна 0.

При х=-1 имею схему:

Я вижу, что -1-корень f и в частном получается многочлен g=x³-2x²-4x+3.

Значение х=1 второй раз проверять незачем: если бы число 1 было корнем g, то оно было бы корнем f, что неверно. Значение х=-1 проверить обязательно – ничто не мешает ему быть также и корнем частного g:

Следовательно, g(-1)≠0

Составлю схему Горнера для х=3:

Следовательно, g(3)=0, и при делении g на х-3 получается многочлен x²+x-1, корни которого . Таким образом, многочлен f, а значит, и исходное уравнение имеют 4 корня: -1, 3 и  .

Теорема Безу позволяет частично ответить и на важный теоретический вопрос: сколько корней может иметь многочлен?

Теорема 2

Многочлен степени n имеет не более n корней.

Д о к а з а т е л ь с т в о. Пусть многочлен f степени n имеет k корней и с – один из его корней. Предположу противное: пусть k>n.

По теореме Безу f=(x-c)g и частное g имеет степень n-1. Всякий корень f, отличный от с, является одновременно и корнем g: если f(а)=0, то (а-с)g(а), откуда g(а)=0, так как а≠с. Другими словами, многочлен g имеет по меньшей мере k-1>n-1 корней, т.е. число его корней также больше его степени.

Но с многочленом g можно провести те же рассуждения и на втором шагу получить новый многочлен h, число корней которого также больше его степени. Продолжая таким же образом, я приду к многочлену степени 2, имеющему больше двух корней, чего не может быть.

Полученное противоречие показывает, что предположение k>n неверно, и, следовательно, k не больше n.

Нетрудно привести примеры, когда многочлен степени n имеет ровно n корней и когда он имеет меньше n корней, в частности, вообще не имеет корней. Эти примеры полезно придумать самостоятельно.

При этом следует иметь в виду, что число корней многочлена существенно зависит от того, какое числовое множество мы рассматриваем.

Например, многочлен f=x²-2 не имеет корней в множестве рациональных чисел Q – не существует рационального числа, квадрат которого равен 2. В то же время в множестве действительных чисел R он имеет два иррациональных корня (±√2).

Из теоремы о числе корней вытекают два исключительно важных и для теории, и для практики утверждения.

Теорема 3.

Два многочлена степени, не большей n, принимают одинаковые значения по меньшей мере при n+1 значениях х тогда и только тогда, когда при каждой степени х они имеют одинаковые коэффициенты.

Д о к а з а т е л ь с т в о. «В одну сторону» это утверждение очевидно: если многочлены имеют одинаковые коэффициенты, то при всех значениях х они, естественно, принимают одинаковые значения.

И наоборот, если многочлены f и g имеют степень не больше n, то их разность h либо является нулевым многочленом, а тогда при каждой степени х они имеют одинаковые коэффициенты, либо отлична от нуля и имеет степень не больше n. Но тогда эта разность имеет не меньше чем n+1 корень – это те значения переменной х=хi, при которых h(xi)=f(xi)-g(xi)=0, что противоречит теореме 2 о числе корней: число корней разности больше её степени.

Теорема 4.

Два многочлена принимают одинаковые значения при всех значениях х тогда и только тогда, когда при каждой степени х они имеют одинаковые коэффициенты.

Д о к а з а т е л ь с т в о. Это утверждение моментально следует из предыдущего: если многочлены принимают одинаковые значения при всех значениях х, то они принимают одинаковые значения при числе значений, большем наибольшей из их степеней.

Итак, я решила общую теоретическую задачу нахождения рациональных корней многочленов с целыми коэффициентами. Если же многочлен не имеет рациональных корней, то задача нахождения его корней может оказаться неразрешимой.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                    Заключение

В процессе моей работы над проектом мной было изучено применение теории многочленов в решении уравнений, были рассмотрены основные понятия, теоремы и алгоритмы. Так же я изучила и продемонстрировала применение основной теоремы (Ж.Безу) и основной схемы (Горнера) для решения уравнений, степени больше 2.

Достоинством теоремы многочленов в решении уравнений является то, что она универсальна. Теорема представляет собой математический аппарат для решения задач более широкого содержания.

Обобщив и систематизировав знания по теореме многочленов и её составляющих, я убедилась в необходимости знаний по теме «Теория многочленов в решении уравнений». Благодаря основательному изучению теоретического материала, для меня стало возможным применить полученные знания для решения многих математических задач, которые раньше были мне не под силу. Кроме того, эти знания повышают интерес к математике, как к науке.